绕轴旋转圆柱结冰特性结冰风洞试验
李岩, 王绍龙, 易贤, 周志宏, 郭龙
1.东北农业大学 工程学院, 哈尔滨 150030 2.中国空气动力研究与发展中心 空气动力学国家重点试验室, 绵阳 621000
绕轴旋转圆柱结冰特性结冰风洞试验
李岩1,*, 王绍龙1, 易贤2, 周志宏2, 郭龙2
1.东北农业大学 工程学院, 哈尔滨 150030 2.中国空气动力研究与发展中心 空气动力学国家重点试验室, 绵阳 621000
绕轴旋转物体结冰是一种常见的结冰现象,如风力机叶片和直升机旋翼结冰等。针对该旋转模型的结冰问题,以绕轴旋转圆柱为对象,进行了结冰风洞试验研究。试验在自行设计的利用自然低温的结冰风洞系统中完成。在对结冰风洞试验能力进行验证后,对具有不同直径、转速和结冰时间的旋转圆柱结冰进行了试验,建立了旋转圆柱的结冰分析与评价方法,分析了转速、圆柱直径、结冰时间等对圆柱结冰形状主要特征量的影响规律,包括结冰面积、无因次结冰面积、驻点厚度、无因次驻点厚度、驻点偏转角、无因次结冰上下极限等,获得了旋转圆柱的结冰特性。在此基础上,通过回归正交试验设计,构建了旋转圆柱结冰的预测模型,并进行了验证与分析。研究结果可为绕轴旋转物体结冰特性研究提供参考和借鉴。
结冰; 旋转圆柱; 结冰风洞试验; 结冰特性; 回归分析
旋转叶片在含有过冷水滴的气流中作业会发生覆冰现象,如风力机叶片结冰,直升机旋翼结冰等[1-2]。叶片结冰后会破坏其气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[3-5]。与平动式叶片结冰相比,旋转叶片结冰研究相对较少,多是在平动式叶片结冰研究基础上的改进与优化。
目前针对结冰研究的主要手段有3种:实际观测、数值模拟计算及结冰风洞试验,随着计算技术及冰风洞技术的发展,数值模拟计算与结冰风洞试验逐渐成为了主要研究手段[6-8]。国外对三维绕轴旋转模型的结冰数值模拟计算较多,如商用结冰仿真软件LEWICE和FENSAP-ICE等均有三维旋转模型结冰计算模块[9-10],国内也有三维结冰计算相关研究,如易贤等对水平轴风力机结冰进行三维计算[11-12],以及关于直升机旋翼结冰数值计算[13-14]。对于绕轴旋转模型结冰风洞试验研究, Han等在美国宾夕法尼亚大学搭建了旋转叶片结冰试验系统[15],该研究主要对不同工况下风力机叶片结冰冰形的外观进行描述,而未对结冰冰形进行参数化分析与预测。国内对绕轴旋转模型的结冰风洞试验系统的构建与研究报道还较少。
本研究通过自行设计的利用自然低温的结冰风洞系统对绕轴旋转圆柱进行结冰试验研究。首先对试验系统的试验能力进行验证;然后对具有不同直径、转速和结冰时间的旋转圆柱进行结冰试验并分析,获得结冰规律。在此基础上,利用正交试验设计方法得出旋转圆柱无因次结冰面积及无因次驻点厚度的预测方程,并进行验证与分析。
1 试验设备与方法
1.1 试验设备
试验在东北农业大学风能研究室自行设计的利用自然低温的结冰风洞系统中完成,如图1和图2所示[16]。基础风洞为日本鸟取大学设计制造的开口射流风洞,在风洞的吹出口处安装水雾喷射系统提供结冰条件,在其后设置喷雾段、混合段和结冰试验段,试验段截面为0.6 m×0.6 m,风速范围为1~15 m/s。冬季室外冷空气由冷风段吸入,与喷雾系统喷出的过冷水滴在混合段充分混合后作用于试验模型上形成结冰。圆柱固定在试验台的旋转梁上,转轴后接调频电机用以控制圆柱绕轴的转速。调频电机位于气道外部不影响结冰,旋转部分位于气道内部。
圆柱模型如图3所示,材质为铝制,直径d=20,30,40 mm,高h=20 mm。
图1 结冰风洞试验台
Fig.1 Icing wind tunnel test rig
图2 结冰风洞试验系统
Fig.2 Icing wind tunnel test system
图3 试验圆柱
Fig.3 Cylinders for test
图4 旋转圆柱运动参数
Fig.4 Motion parameters of rotating cylinder
1.2 试验方法
旋转圆柱试验运动参数如图4所示,U为来流风速,ω为旋转速度。试验过程中,圆柱模型随着转轴做圆周运动,利用高速摄像机(美国Phantom v5.1,分辨率为1 024×1 024像素)拍摄圆柱结冰。
试验在2015年冬季进行,其中结冰风洞相关参数标定在作者的前期研究中给出了介绍[16],主要包括试验段温度稳定性验证、试验段截面液态水含量分布标定及过冷水滴直径标定。
2 试验结果与分析
2.1 结冰风洞试验能力验证
通过结冰风洞试验获得的典型旋转圆柱结冰,如图5所示,不同圆柱直径对结冰冰形影响较大,沿圆柱展向的结冰外形基本没有变化。
在3根旋转梁上加装相同直径(d=30 mm)的圆柱进行结冰试验。结冰试验条件为:结冰时间t=10 min;结冰温度T=-8 ℃;来流风速U=4.54 m/s;液态水含量LWC=0.5 g/m3;过冷水滴平均粒径MVD=40 μm;绕轴旋转直径D=0.5 m;选取了两个旋转速度ω,分别为200 r/min 和400 r/min。
图6为圆柱结冰重复性验证试验结果。可以发现,在相同的试验环境下,不同旋转梁上的圆柱模型结冰分布几乎相同。通过上述分析可见在结冰风洞试验段内,圆柱旋转区域的来流速度稳定,液态水含量分布均匀,状态稳定,所设计的利用自然低温的结冰风洞试验系统满足旋转圆柱结冰试验研究的要求,能较好模拟实际结冰气象条件。
图5 典型旋转圆柱结冰
Fig.5 Typical ice of rotating cylinder
图6 圆柱结冰重复性验证
Fig.6 Verification of repeatability of cylinder icing
2.2 结冰影响因素分析
2.2.1 结冰分布
在进行结冰影响因素分析中,确定结冰试验条件为:结冰温度T=-8 ℃;来流风速U=4.54 m/s;液态水含量LWC=0.5 g/m3;过冷水滴平均粒径MVD=40 μm;绕轴旋转直径D=0.5 m;选取3种直径的圆柱,分别为20,30,40 mm;选取2个结冰时间:t=5,10 min;选取5个旋转速度:ω=100,200,400,600,800 r/min。
图7 不同工况圆柱结冰
Fig.7 Cylinder icing under different working conditions
图7给出了不同工况的圆柱结冰情况。分析不同转速对圆柱结冰影响,当转速小于200 r/min时,圆柱表面结冰量较少,冰形平滑,基本保持圆弧形状;当转速为400 r/min时,结冰量有所增加,冰形前端仍然保持圆弧形状,两侧部分不再平滑而变成近似直线;当转速为600 r/min时,结冰量增加更多,冰形两侧部位仍然保持近似直线,前缘部分不再为圆弧状而变为了前缘凸起的弧线;当转速为800 r/min时,冰形前缘部分不再为弧线而变成平线,两侧出现较大折弯,积冰向角状冰趋势发展。
分析不同结冰时间对圆柱结冰影响,在其他环境参数相同的工况下,随着结冰时间的增长,结冰量增长明显,但冰形分布特点变化较小。
分析不同直径对圆柱结冰影响,在其他环境参数相同的工况下,圆柱结冰冰形分布特点变化较小,在一定尺度范围内,相同外形不同尺寸旋转模型结冰分布特点相同,但由于直径不同,圆柱表面结冰发展趋势产生较大差别。
整体而言,相对于静止工况下的圆柱结冰,旋转圆柱结冰冰形的迎风面与非迎风面是非对称的,产生该种现象的原因在于旋转状态下圆柱的过冷水滴的撞击特性有别于静止状态下的过冷水滴撞击特性,来流水滴不能对称地撞击到旋转圆柱上。
2.2.2 结冰特征量
图8 圆柱结冰典型特征量
Fig.8 Typical characteristics of cylinder icing
为了更直观地研究旋转圆柱结冰规律,对不规则的冰形进行量化分析,针对本研究中获得的二维结冰冰形,凝练出典型特征量,建立旋转圆柱结冰冰形分析与评价方法[17-19]。图8为旋转圆柱结冰冰形典型特征量:结冰面积S、结冰驻点厚度σ、结冰驻点偏转角α、结冰上极限Lu及结冰下极限Ld。其中不规则冰形的面积为结冰面积S,冰形距离圆柱中心的最远点与圆柱轮廓的垂直距离为驻点厚度σ,驻点厚度线与圆柱的圆周速度V的夹角为驻点偏转角α,圆周速度V与圆柱轮廓的交点到冰形轮廓与圆柱轮廓相交的最远点间的弧长分别为结冰上极限Lu及结冰下极限Ld。
对于不同直径的圆柱,其结冰的特征量相互比较,存在基准不一的情况,对其典型特征量进行无量纲化,需引入以下无因次参数。
无因次结冰面积ηS:
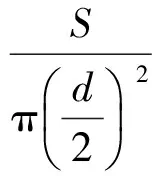
(1)
无因次结冰驻点厚度ησ:
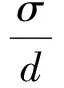
(2)
无因次结冰上极限ηLu:
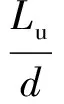
(3)
无因次结冰下极限ηLd:

(4)
图9给出了不同工况下圆柱结冰面积S的变化情况。分析转速对结冰面积S的影响,在其他条件均相同时,转速越大,单位时间内结冰面积越大,结冰面积呈单调增长趋势,这是由于随着转速的增加,空气中的过冷水滴更难穿过相邻圆柱间的空隙,单位时间内有更多的过冷水滴被圆柱捕捉,进而使结冰面积增大。分析结冰时间对结冰面积S的影响,在其他条件均相同时,圆柱结冰面积随结冰时间增长而增加,结冰10 min的结冰面积约为结冰5 min的结冰面积的两倍,这是由于结冰时间越长,圆柱捕获的过冷水滴越多,结冰面积越大。分析圆柱直径对圆柱结冰面积S的影响,在其他条件相同时,随着圆柱直径的增加,结冰面积也相应增加,这是由于直径增大,圆柱的迎风面变大,能够更多地捕获来流中的过冷水滴。
图10给出了不同工况下圆柱结冰无因次结冰面积ηS的变化情况。分析上述影响因素对无因次结冰面积ηS的影响,其中转速、结冰时间对旋转圆柱无因次结冰面积的影响趋势与对结冰面积的影响趋势相同,不对其作分析。需要指出的是圆柱直径对无因次结冰面积影响较大,随着直径的增加,虽然旋转圆柱捕获了更多的过冷水滴从而获得了较大的结冰面积,但其无因次结冰面积反而是降低的,其对圆柱模型外轮廓的改变程度也相应的较小,可认为在相同工况下小外形的模型更易受到结冰的影响。
图9 不同工况的圆柱结冰面积
Fig.9 Cylinder icing area under different working conditions
图10 不同工况的圆柱无因次结冰面积
Fig.10 Cylinder dimensionless icing area under different working conditions
图11给出了不同工况下圆柱结冰驻点厚度σ的变化情况。分析转速对结冰驻点厚度σ的影响,在其他条件均相同时,转速越大,单位时间内的驻点厚度增长越大,驻点厚度也越大,呈单调增长趋势,这是由于随着转速的增加,更多的过冷水滴被圆柱捕捉,进而使驻点厚度增大;分析结冰时间对驻点厚度σ的影响,在其他条件均相同时,随着结冰时间增加,驻点厚度呈增长趋势,这是由于结冰时间越长,圆柱捕获的过冷水滴越多,驻点厚度越大;分析圆柱直径对驻点厚度σ的影响,在其他条件相同时,不同直径的圆柱结冰驻点厚度几乎相同,这是由于虽然直径的增加能够捕捉更多的过冷水滴,但是在单位时间内撞击到驻点位置的过冷水滴数量是相近的,形成的结冰厚度也是相近的。
图12给出了不同工况下圆柱结冰无因次结冰驻点厚度ησ的变化情况。分析上述影响因素对无因次驻点厚度ησ的影响,其中转速、结冰时间对旋转圆柱无因次结冰驻点厚度的影响趋势与其对结冰驻点厚度的影响趋势相同,不对其作分析。同时,虽然不同直径的圆柱结冰驻点厚度几乎相同,但无因次结冰驻点厚度却降低了,同样验证了相同工况下小外形模型更易受到结冰的影响。
图11 不同工况的圆柱结冰驻点厚度
Fig.11 Cylinder icing stagnation thickness under different working conditions
图12 不同工况的圆柱无因次结冰驻点厚度
Fig.12 Cylinder dimensionless icing stagnation thickness under different working conditions
图13给出了不同工况下圆柱结冰驻点偏转角α的变化情况。其中转速对结冰驻点偏转角影响较大,结冰时间及圆柱直径对其几乎没有影响。
图14给出了不同工况下圆柱结冰无因次结冰上极限ηLu的变化情况。图15给出了不同工况下圆柱结冰无因次结冰下极限ηLd的变化情况。
图13 不同工况的圆柱结冰驻点偏转角
Fig.13 Cylinder icing stagnation deflection angle under different working conditions
图14 不同工况的圆柱结冰无因次结冰上极限
Fig.14 Dimensionless icing upper limit of cylinder icing under different working conditions
图15 不同工况的圆柱结冰无因次结冰下极限
Fig.15 Dimensionless icing lower limit of cylinder icing under different working conditions
其中转速对无因次结冰上下极限影响较大,结冰时间及圆柱直径对其几乎没有影响。同时可以发现虽然随着转速的增加,无因次结冰上极限在逐渐减小,无因次结冰下极限在逐渐增加,但两者之和是一个定值,且接近于圆柱周长的一半。
根据上述分析,转速是影响驻点偏转角、结冰上下极限的主要原因,旋转过程中圆柱的相对速度变化情况如图16所示,Rω1~Rω 5为旋转半径,W1~W5为相对速度。可以发现随着转速的增加,圆柱的相对速度与垂线的夹角逐渐变小,其变化趋势也是先快后慢,与试验数据趋势相同。旋转过程中圆柱的迎风面变化情况如图17所示,随着圆柱的迎风迎角的变化,迎风面也发生相应的偏转,其中结冰上极限随着转速增加而减小,结冰下极限随着转速增加而增大,但是随着转速增加这一趋势逐渐放缓,这与试验数据相对应。同时虽然迎风面角度改变,但是迎风面的大小保持不变,即圆柱结冰上极限与下极限之和是恒定的,这与试验数据也相互对应。
图16 旋转过程中圆柱相对速度变化情况
Fig.16 Change of cylinder relative velocity in process of rotation
图17 旋转过程中圆柱迎风面变化情况
Fig.17 Change of cylinder frontal plane in process of
rotation
3 结冰特征量回归模型建立
3.1 正交回归试验设计
旋转圆柱模型结冰过程包含一系列的物理变化,影响其结冰的主要参数可归纳为结冰时间、来流风速、旋转速度、环境温度、液态含水量等,同时,圆柱结冰的冰形为不规则图形,典型特征量很多,寻找这些变量的相关关系,通过回归分析的数据处理方法确立回归方程,可以实现对典型特征量的预测。但是由于考察因素较多,而且每个因素的水平也较多,如果对每个因素进行分析并相互搭配进行试验,工作量相当庞大。正交试验设计是研究多因素多水平的试验设计方法,能够通过较少的试验次数获得较好的试验结果,但是该种试验结果只限制在已有的水平中。将正交试验设计与回归分析相结合,不仅能得到合理的试验设计方案和较少的试验次数,还能建立数学模型进行预测[20]。通过该方法得到预测模型结果的时间要远低于通过CFD数值计算获得预测结果的时间,且计算过程中耗费的计算资源更少。
本文在进行单因素试验研究的基础上,对旋转圆柱结冰进行正交组合试验。确定结冰试验条件为:结冰温度T=-8 ℃;液态水含量LWC=0.5 g/m3;过冷水滴平均粒径MVD=40 μm;绕轴旋转直径D=0.5 m;圆柱模型直径d=30 mm。
试验根据中心正交组合设计原理,采用3因素5水平对结冰时间tX1、来流速度UX2、圆柱旋转角速度ωX3对圆柱结冰影响情况进行分析,设计水平表见表1,分别以无因次结冰面积ηS(R1)、无因次结冰驻点厚度ησR2为响应值。根据所设计的试验方案进行试验,获得圆柱结冰试验结果图片后进行处理,取特征量进行分析。

表1 中心组合水平表Table 1 Central composite level table
3.2 试验结果与分析
采用Design Expert 8.0.6软件进行试验设计,试验方案及试验结果见表2,对试验数据进行回归分析和拟合优化,去掉回归模型中不显著项,得到圆柱结冰的无因次结冰面积ηS、无因次结冰驻点厚度ησ与计算因素的回归方程,如表3所示。
为了验证回归模型的准确性,将回归方程曲线与设计方案中未出现的结冰试验条件下的旋转圆柱试验值进行比较。其中试验条件为:结冰时间t=5 min;来流风速U=4.54 m/s;旋转速度ω=100,200,400,600,800 r/min。图18给出了无因次结冰面积ηS的试验值与预测模型的对比情况,可以发现预测模型与试验值具有较高的吻合性。同理图19给出了无因次结冰驻点厚度ησ的试验值与预测模型的对比情况,可以发现预测模型与试验值同样具有较高的吻合性。
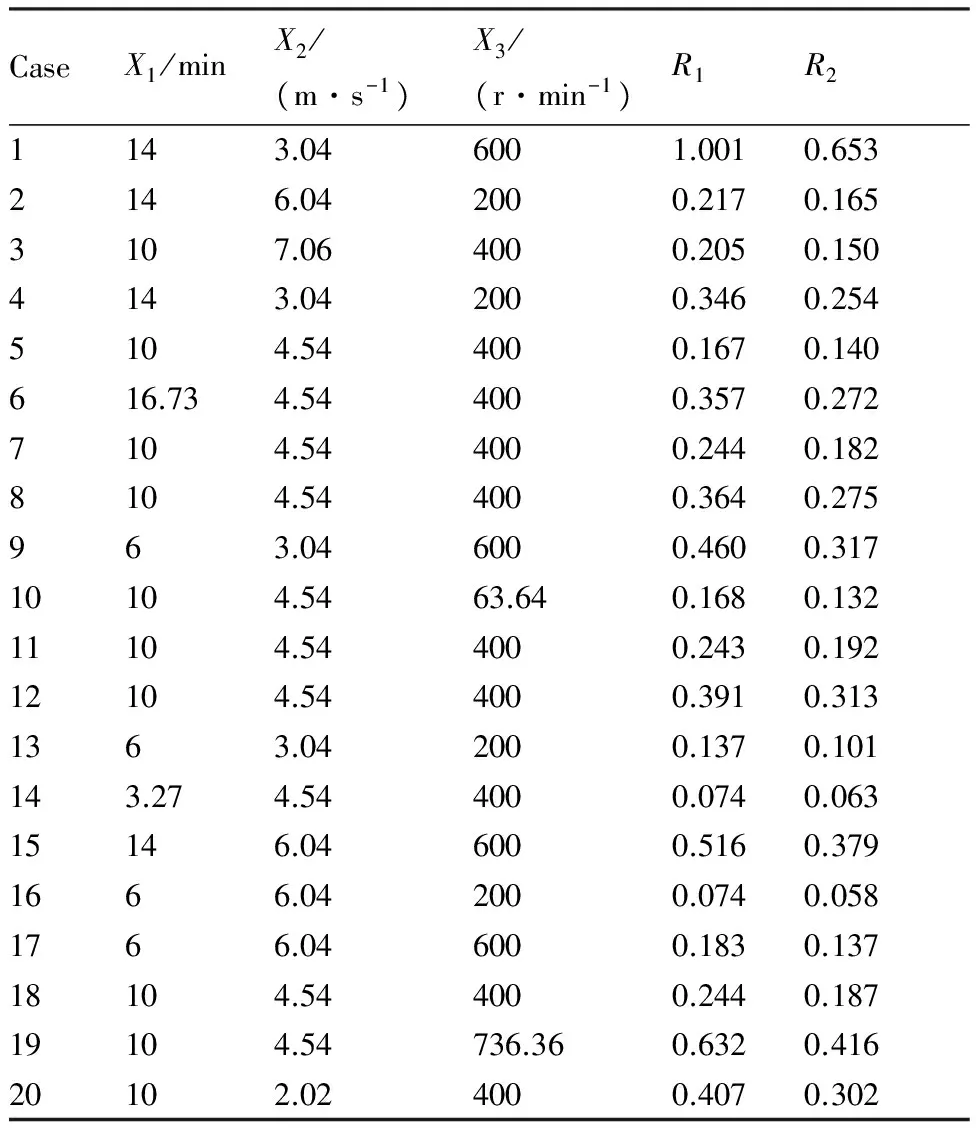
表2 试验设计方案及结果Table 2 Test design cases and results
采用上述方法同样可以建立圆柱结冰其他典型特征量回归方程,在此不作详细描述。发现通过上述的回归方程,能够很快得到旋转柱结冰典型特征量,该方法也可用于旋转叶片的结冰特征量的回归建模,进而为结冰检测与防除冰系统开发提供帮助。
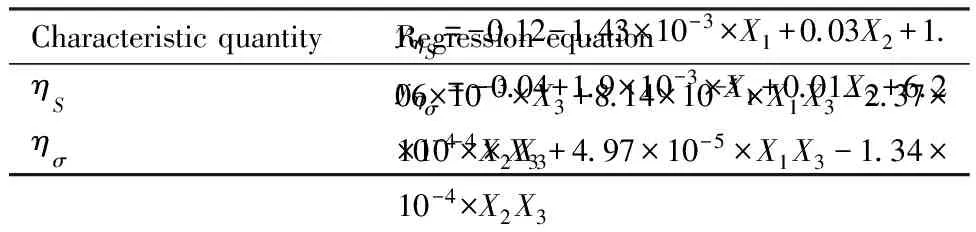
表3 特征量回归方程Table 3 Characteristic quantity regression equations
4 结 论
1) 可以利用自然低温的冰风洞试验系统对绕轴旋转圆柱等旋转模型进行结冰试验研究。
2) 转速越大,绕轴旋转圆柱单位时间内结冰面积越大,总的结冰面积也越大,驻点厚度与结冰面积趋势相同,驻点偏转角减小,结冰上极限减小,结冰下极限增大,且这3个特征量变化趋势随转速增加而减缓。
3) 随着结冰时间的增加,绕轴旋转圆柱的结冰面积及驻点厚度呈增长趋势,对驻点偏转角、结冰上下极限影响较小。
4) 随着圆柱直径增大,绕轴旋转圆柱的结冰面积相应增大,但无因次结冰面积反而减小;结冰驻点厚度不受圆柱直径的影响,但无因次驻点厚度相应减小,即小模型更易受到结冰的影响,对驻点偏转角、结冰上下极限几乎没有影响。
5) 通过正交试验获得了绕轴旋转圆柱无因次结冰面积及无因次结冰驻点厚度的回归模型方程,其预测趋势与试验结果具有较高吻合性。利用该方法可在一定程度上对绕轴旋转模型进行结冰预测。
[1] MAKKONEN L, LAAKSO T, MARJANIEMI M, et al. Modeling and prevention of ice accretion on wind turbine on wind turbines[J]. Wind Engineering, 2001, 25(1): 3-21.
[2] 徐玉貌, 吕少杰, 曹义华, 等. 旋翼桨叶结冰对直升机飞行性能的影响[J]. 航空动力学报, 2016, 31(2): 399-404.
XU Y M, LÜ S J, CAO Y H, et al. Effects of rotor blade icing on helicopter flight performance[J]. Journal of Aerospace Power, 2016, 31(2): 399-404 (in Chinese).
[3] 任鹏飞, 徐宁, 宋娟娟, 等. 结冰对风力叶片影响数值的数值研究[J]. 工程热物理学报, 2015, 36(2): 313-317.
REN P F, XU N, SONG J J, et al. Numerical research on impact of icing on wind turbine blades [J]. Journal of Engineering Thermophysics, 2015, 36(2): 313-317 (in Chinese).
[4] 严晓雪, 朱春玲, 王正之.风力机冰脱落轨迹仿真研究[J]. 计算机仿真, 2015, 32(10): 123-127.
YAN X X, ZHU C L,WANG Z Z. Numerical simulation of ice shedding from wind turbine[J].Computer Simulation, 2015, 32(10): 123-127 (in Chinese).
[5] 李国之, 曹义华. 直升机旋翼结冰后的飞行品质[J]. 南京航空航天大学学报, 2011, 43(3): 381-386.
LI G Z, CAO Y H. Effects of rotor icing on flying qualities of helicopter[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(3): 381-386 (in Chinese).
[6] MILLER T L, KORKAN K D, SHAW R J. Analytical determination of propeller performance degradation due to ice accretion[J].Journal of Aircraft, 1987, 24(11): 768-775.
[7] 陈科, 曹义华, 潘星. 改进的翼型积冰数值模拟方法[J]. 航空动力学报, 2007, 22(11): 1814-1819.
CHEN K, CAO Y H, PAN X. An improved numerical simulation method for airfoil ice accretion [J]. Journal of Aerospace Power, 2007, 22(11): 1814-1819 (in Chinese).
[8] 战培国. 国外寒冷地区风力机结冰问题研究[J]. 航空科学技术, 2016, 27(2): 1-6.
ZHAN P G. Review of the wind turbine icing in overseas cold regions[J]. Aeronautical Science & Technology, 2016, 27(2):1-6 (in Chinese).
[9] RUFF G A, BERKOWITZ B M. Users manual for the NASA lewis ice accretion prediction code (LEWICE): NASA CR-185129[R]. Washington, D.C.: NASA, 1990.
[10] TAIKI M, MASAYA S, MAKOTO Y,et al. Numerical simulation of ice accretion phenomena on rotor blade of axial blower[J]. Journal of Thermal Science, 2012, 21(4): 322-326.
[11] 易贤, 王开春, 马洪林, 等. 水平轴风力机结冰及其影响计算分析[J]. 太阳能学报, 2014, 35(6): 1052-1058.
YI X, WANG K C, MA H L, et al. Computation of icing and its effect of horizontal axis wind turbine[J]. Acta Energiae Solaris Sinica, 2014, 35(6): 1052-1058 (in Chinese).
[12] 易贤, 王开春, 马洪林, 等. 大型风力机结冰过程水滴收集率三维计算[J]. 空气动力学学报, 2013, 31(6): 745-751.
YI X, WANG K C, MA H L, et al. 3-D numerical simulation of droplet collection efficiency in large-scale wind turbine icing[J]. Acta Aerodynamica Sinica, 2013, 31(6): 745-751 (in Chinese).
[13] 李国之, 曹义华, 钟国. 旋翼结冰模型与纵列式直升机平衡特性分析[J]. 北京航空航天大学学报, 2010, 36(9): 1034-1037.
Li G Z, CAO Y H, ZHONG G. Rotor icing model and trim characteristics analysis for tandem helicopter[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(9): 1034-1037 (in Chinese).
[14] 陈希, 招启军, 赵国庆. 计入离心力影响的直升机旋翼翼型结冰数值模拟[J]. 航空动力学报, 2014, 29(9): 2157-2165.
CHEN X, ZHAO Q J, ZHAO G Q. Numerical simulation of ice accretion on rotor airfoil of helicopter considering effects of centrifugal force[J]. Journal of Aerospace Power, 2014, 29(9): 2157-2165 (in Chinese).
[15] HAN Y Q,PALACIOS J, SCHMITZ S. Scaled ice accretion experiments on a rotating wind turbine blade[J]. Journal of Wind Engineering and Industrial Aerodynamica, 2010, 109: 55-67.
[16] 李岩, 王绍龙, 郑玉芳, 等. 利用自然低温的风力机结冰风洞试验系统设计[J]. 实验流体力学, 2016, 30(2): 54-58, 66.
LI Y, WANG S L, ZHENG Y F, et al. Design of wind tunnel experiment system for wind turbine icing by using natural low temperature[J]. Journal of Experiment in Fluid Mechanics, 2016, 30(2): 54-58, 66 (in Chinese).
[17] RUFF G A. Quantitative comparison of ice accretion shapes on airfoils[J]. Journal of Aircraft, 2002, 39(3): 418-426.
[18] 周志宏, 易贤, 郭龙, 等. 基于云雾参数误差的结冰外形修正方法[J]. 实验流体力学, 2016, 30(3): 8-13.
ZHOU Z H, YI X, GUO L, et al. Ice shape correction method based on the error of cloud parameters[J]. Journal of Experiment in Fluid Mechanics, 2016, 30(3): 8-13 (in Chinese).
[19] BRAGG M B, GREGOREK G M. Aerodynamic characteristics of airfoils with ice accretions[C]//AIAA 20th Aerospace Sciences Meeting. Reston: AIAA, 1992.
[20] 李云雁, 胡传荣. 实验设计与数据处理[M]. 北京: 化学工业出版社, 2005.
LI Y Y, HU C R. Experimental design and date processing[M]. Beijing: Chemical Industry Press, 2005 (in Chinese).
(责任编辑: 李明敏)
URL:www.cnki.net/kcms/detail/11.1929.V.20161214.1629.002.html
Anicingwindtunneltestonicingcharacteristicsofcylinderrotatingaroundashaft
LIYan1,*,WANGShaolong1,YIXian2,ZHOUZhihong2,GUOLong2
1.EngineeringCollege,NortheastAgriculturalUniversity,Harbin150030,China2.StateKeyLaboratoryofAerodynamics,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China
Icingontheobjectsrotatingaroundashaftisacommonphenomenon,suchasicingonwindturbinebladeandhelicopterpropeller.Inordertoinvestigatetheicingcharacteristicsoftherotatingmodel,icingwindtunneltestsarecarriedoutonthecylinderrotatingaroundashaft.Testsareperformedintheicingwindtunnelsystemwithnaturallowtemperatureincoldclimate.Therepeatabilityvalidationtestismadefortheicingonrotatingcylinder.Icingtestsarecarriedoutontherotatingcylinderwithdifferentrotatingspeed,cylinderdiameterandicingtime.Analysisandevaluationmethodsfortheicingcharacteristicsoftherotatingcylinderareestablished.Theeffectsofthesefactorsonthecharacteristicsoficingshapeonrotationcylinderareexplored,includingicingarea,dimensionlessicearea,stagnationthickness,dimensionlessstagnationthickness,stagnationpointdeflectionangle,anddimensionlessicingupperandlowerlimits.Theicingcharacteristicsoftherotatingcylinderareobtained.Basedontheaboveresearch,theregressionequationsforcalculatingtheicingcharacteristicsofrotatingcylinderareobtainedthroughorthogonalexperimentaldesignmethod,andthepredictionmodelfortherotatingcylinderisdeveloped.Comparisonandverificationanalysisofthetestandthepredictionvaluesarecarriedout.Theresearchresultscanprovidereferenceforthestudyoficingcharacteristicsontheobjectrotatingaroundashaft.
icing;rotatingcylinder;icingwindtunneltest;icingcharacteristics;regressionanalysis
2016-08-23;Revised2016-10-10;Accepted2016-11-30;Publishedonline2016-12-141629
s:NationalNaturalScienceFoundationofChina(51576037,11172314);NationalBasicResearchProgramofChina(2015CB755800)
.E-mailliyanneau@163.com
2016-08-23;退修日期2016-10-10;录用日期2016-11-30; < class="emphasis_bold">网络出版时间
时间:2016-12-141629
www.cnki.net/kcms/detail/11.1929.V.20161214.1629.002.html
国家自然科学基金 (51576037,11172314); 国家“973”计划 (2015CB755800)
.E-mailliyanneau@163.com
李岩, 王绍龙, 易贤, 等. 绕轴旋转圆柱结冰特性结冰风洞试验J. 航空学报,2017,38(2):520693.LIY,WANGSL,YIX,etal.AnicingwindtunneltestonicingcharacteristicsofcylinderrotatingaroundashaftJ.ActaAeronauticaetAstronauticaSinica,2017,38(2):520693.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0314
V211.73
A
1000-6893(2017)02-520693-11

