利用两次最大似然估计的单站外辐射源时差定位算法

张玉灵，何 俊，朱健东，戴幻尧

(1.郑州升达经贸管理学院， 河南 郑州 451191；2.洛阳电子装备试验中心，河南 洛阳 471003)

利用两次最大似然估计的单站外辐射源时差定位算法

张玉灵1，何 俊1，朱健东2，戴幻尧2

(1.郑州升达经贸管理学院，河南郑州451191；2.洛阳电子装备试验中心，河南洛阳471003)

针对多站外辐射源定位系统复杂度高问题，提出了一种单站外辐射时差(TDOA)定位算法。该算法利用两次最大似然估计算法分步解相关得到目标的精确位置。仿真结果表明，时差误差较小时，估计的均方误差(MSE)接近CRLB，随着目标远离观测站，定位误差随之增大，目标距离地面的高度越低，z轴的估计误差越大。该方法利用单站接收目标的多个信号时差信息进行定位，能够克服多站定位中时间同步困难等问题。

单站外辐射源定位；最大似然估计；时差定位；CRLB

0 引言

基于外辐射源的无源定位方法，又称被动协同定位(Passive Coherent Location, PCL)方法。由于该技术在航空和电子领域的广泛应用，以及其相比于主动雷达具有体积小、高隐蔽性、低空探测能力等优点[1]，近年来成为各研究机构和学校的研究热点。可用于定位的外辐射源包括调频广播 (Frequency Modulation, FM)[2]信号、数字电视 (DVB-T)[3-4]信号、手机信号基站WiFi[5]等常见的民用信号。相比于多站系统，单站系统机动性强、成本低，且不存在时间和数据同步的问题。因此研究高精度的单站外辐射源定位方法具有重要的意义。

目标的定位算法主要包括利用接收信号强度(RSS)的算法[6]，利用信号到达方向(DOA)[7-8]以及利用信号的传播时间(TOA, TDOA)的算法[9]。如果被定位的目标是移动的，还可利用接收信号的频差(FDOA)[10]来实现目标的定位，另外还有根据信号接收站的特点联合多种信息的定位方法[7,10]。不同的观测信息使系统的复杂度不同，信息量越少越单一，系统越简单；信息量越多，系统越复杂。所以模型的确定需根据实际而定。

现有基于到达时间的定位方法主要是针对目标辐射源定位的多站系统[11-12]，系统硬件复杂度高。针对多站外辐射源定位系统复杂度高问题，提出了利用两次ML估计的单站外辐射TDOA定位算法。采用两步最大似然估计算法实现对目标的精确定位，并将定位的结果与CRLB比较，同时分析了定位算法的性能。

1 单站外辐射源定位方法

无源定位系统大致可以分为两种类型：多站系统和单站系统。多站系统需要各站之间同步工作并进行大量的数据传输，此外还要求对集中的数据进行融合处理，使定位系统变得复杂，也限制了系统的机动性，因此，近几年来，单站无源定位技术受到了越来越多的关注。单站无源定位技术是利用一个观测平台被动接收信号来实现的定位技术，主要有两种类型：一是直接对未知位置的辐射源定位；二是利用确定性的且已知地理位置的辐射源，通过测量其照射到目标后反射信号的方位角、俯仰角以及反射信号与直接到达信号的时间差，建立一系列的观测方程，通过解算来确定航行中目标的空间位置。文献[11]提出采用多个接收站同时接收，一个外辐射源经过一个或多个目标散射回来的信号，对目标进行定位。从几何学的角度来看，确定空间一点，可以由三个或三个以上的曲面或平面在三维空间中相交得到，该数学原理在很多文献上均有论述，篇幅所限这里不赘述。

2 利用两次最大似然估计的时差定位算法

提出一种新的单站外辐射源定位方法，定位模型如图1所示。与文献[11]不同，本文定位模型包含单个接收站，N个外辐射源，一个或多个目标，利用单个接收站接收到的多个反射信号到达时间差(TDOA)对目标定位。本文提出的信号定位体制适应于可选外辐射源较多的情形，利用单个接收站即可定位，进而不需要考虑多站之间的时间同步问题。下面分别给出物理模型和非线性数学解算方法。

算法第一步假设需要估计的目标位置x,y,z和距离R为状态量θ=[x,y,z,R]，为便于理解和计算，这里设x,y,z和R不相关，通过ML算法获取θ的估计值。第二步再次通过ML算法实现解相关，得到目标位置估计。

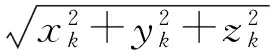
τk=(R+rk-dk)/c+vτk

(1)

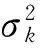
2.1 第一次最大似然估计

对式(1)移项，得：

c(τk-vτk)-R+dk=rk

(2)

对式(2)两边同时平方，化简得：

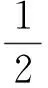
(3)

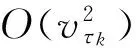
h-Sθ=Bv+O(v2)≈Bv

(4)

式中，

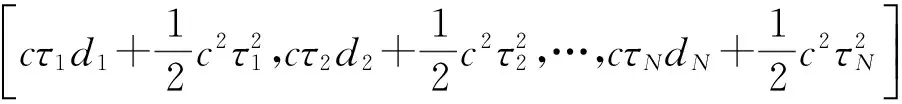
θ=[x,y,z,R] ，

v=[vτ1,…vτN]T，

B=diag(cR-cd1-c2τ1,…,cR-cdN-c2τN) 。

φ=h-Sθ

(5)

根据噪声假设和式(4)可知E[φ]=0，且其协方差矩阵为：

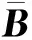
(6)

根据高斯误差向量的特性，假设θ已知时，构建误差向量的概率密度函数为：

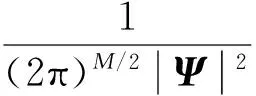
(7)

通过式(7)求解θ的ML解。首先对式(7)求偏导：

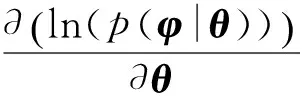
(8)

进而得到：

(9)

当时延的估计误差不是高斯噪声时，式(9)得到的也是最小二乘(LS)解[11]。

但对于定位的问题，式(9)不可直接得到估计结果，因为Ψ矩阵包含的B是θ的函数，所以这里需要用迭代的方法来得的待估参数θ的值。迭代步骤为：

1)选择Ψ一个初值，Ψ0=Q；

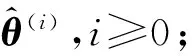
上述迭代的过程可以画成流程图如图2所示。

2.2 第二次最大似然估计

(10)

其中，ei,i=1,2,3,4为步骤1)中的估计误差。

(11)

所以：

(12)

(13)

将式(13)化简并省略高次项：

(14)

求得：

(15)

将式(12)带入式(15)得：

(16)

所以：

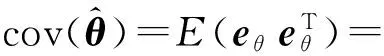
(17)

因为BE[vvT]BT=Ψ，所以式(17)化简为：

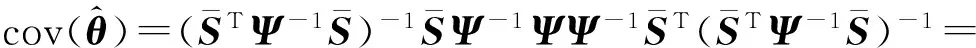
(18)

实际的计算中用步骤1)的估计值来代替真实值。

构建向量：

(19)

将式(10)带入式(19)化简得

(20)

同理于式(6)的推导过程，得：

(21)

(22)

进而得到目标位置：

(23)

(24)

那么，TSE算法的计算步骤可归纳为：

2.3 多目标定位方法

上面针对的场景是单个目标，如果场景内存在多个观测目标，则式(1)将不满足观测方程的要求。此时假设目标为(xj,yj,zj)，其中j=1,2,…,M，M为目标个数。那么观测方程可改写为：

(25)

如果参数估计过程可将第j个目标对应的时延[τ1,τ2,…,τN]T区分出来，可利用本文2.2节和2.3节的算法分别求解得到M个目标的位置。但是，结合图 1所示的定位模型可知，存在M个目标时，会产生MN个时延，如何将MN个时延组合成M个观测方程是多目标估计的难点。

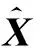
(26)

从参数估计的角度思考多目标问题。可以参照文献[12]的方法获取多目标的大致方位，进而区分不同目标对应的时延，进一步估计出多目标的位置。由于这里主要是区分不同目标对应的参数，所以只需目标的大致方向，所以MIMO雷达的接收端可用干涉仪模型减小计算量。

3 仅用时差定位的CRLB及性能分析

估计误差的克拉美-罗(Cramer-Rao)下限(CRLB)是对定位跟踪问题的有意义并且实际的评价，它揭示了对于所讨论的模型，状态估计误差的统计平均的下限。本节通过推导新算法的估计极限性能的解析表达式，为评估算法性能提供数学依据。

3.1CRLB推导

将式(1)写为向量形式为：

τ=f(X)+v

(27)

式中，τ=[τ1,…,τN]T，X=[x,y,z]T，f(X)=[f1(X),…,fN(X)]T，v=[vτ1,…,vτN]T。根据前文假设，vτi为高斯的，那么可以构建起概率密度函数为：

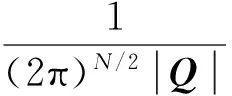
(28)

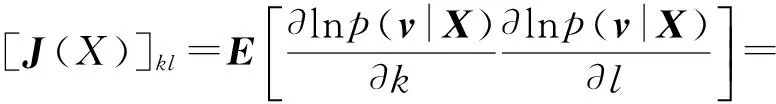
(29)

计算得到FIM的各元素如下：

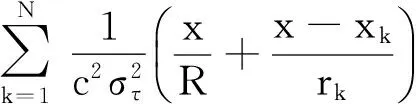
那么系统的估计误差的均方误差MSE满足：

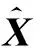
(30)

3.2 性能分析

同理于式(18)的推导过程，得到Υ的估计方差为：

cov(Υ)=(GTΩ-1G)-1

(31)

(32)

式中X.2为对向量中的每个元素分别平方，C=diag(x,y,z)。从而得到最终估计结果的方差为：

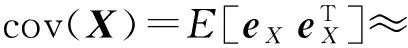
(33)

分别将式(18)，式(21)，式(31)带入式(33)，最终得到

(34)

4 实验仿真

现有的时差定位算法主要是针对基于目标辐射源的多站时差定位法。这类算法虽也适用于本文所研究的模型，如文献[13]利用替换求解的方法获取辐射源位置估计。但是该方法在算法模型中没有考虑误差因素，所以定位的精度不高，同时该算法存在模糊现象。因此本文算法优于文[12]算法。为了验证本文算法的可行性和算法的优越性，将本文算法估计的MSE与CRLB对比，在下文的实验中，应用到的辐射源的位置坐标假设如表1所示。

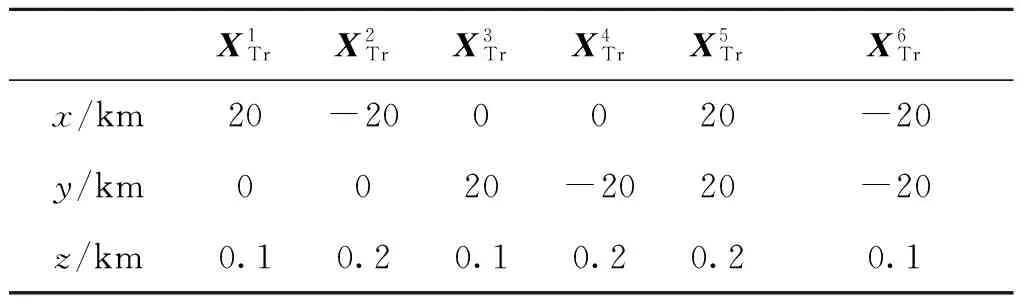
表1 外辐射源的位置

并假设时延的观测误差均相同，根据文献[12]假设时延估计误差变化的范围在10～1 000 ns之间。

实验1：算法定位精度分析

为了验证算法的定位精度，将估计的结果与CRLB对比。首先假设在6个外辐射源的条件下，时延误差为10～1 000 ns之间，取10个观测点，得到目标在[10,10,10] km时的估计结果如图3所示。从图中所示的结果可知，当时延误差较小时，定位精度较高，接近CRLB，当TDOA误差大于100 ns之后，估计误差增大并偏离CRLB，因此后面的仿真，均选择TDOA误差等于100 ns。且z坐标的误差相对与x轴与y轴要大，偏离CRLB也越大。这是由于算法模型是在省略误差高次项的条件下成立的，当观测误差较大时，近似的观测方程不准确，所以估计结果不精确。

当目标远离观测站时，设目标位置为[100,100,10] km时的定位结果如图5所示，在整个时差误差条件下，x、y轴的估计误差的MSE基本接近CRLB。当στi<40 ns时，估计误差的MSE偏离CRLB。

当στi>600 ns之后，定位算法对于z轴基本失去意义了，此时已经不能得到z轴位置估计，所以才会出现MSE低于CRLB的现象。对比图3和图4发现，目标偏离观测站时，估计误差增大。

实验2：步骤1)的迭代次数对估计结果的影响

假设有6个外辐射源，目标位于[10,10,10]km的位置，时延误差标准差为100 ns，得到算法步骤1)中每次迭代的结果与真实目标位置的偏差结果如图5所示。从图5的结果可知，2次迭代就可使步骤1)的估计结果趋于稳定，所以在之后的实验中，迭代步数定为3。

实验3：算法性能分析

目标定位的几何精度因子(Geometric Dilution of Precision, GDOP)为

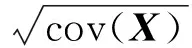
(35)

为了研究目标定位的误差随着目标位置的改变的变化情况，需要在一定的目标位置条件下画出GDOP的等高线图，但是由于等高线图只能有两个变量，所以这里假设目标的高度是确定的条件下的GDOP图。下面给出TDOA误差标准差为100 ns时的GDOP图。

图6到图8给出了不同条件下的GDOP等高线图。从图中可知，随着目标远离观测站，估计误差随之增加，当目标距离观测站100 km左右时达到最大，然后减小，当增加到200 km左右时达到最小，然后增大。从图6和图7可以看出，当目标出现在(-100,100)km和(100,-100)km时误差出现一个最大值现象。通过对比辐射源在坐标轴上的位置，发现在这两个项现刚好没有辐射源，从而出现这个现象。为了验证该问题，图8的GDOP图为8个辐射源。且新增的两个辐射源坐标分别为(20, -20, 0.8)km和(-20, 20, 0.8)km。同时，对比图6和图7可知，相同的误差条件下，目标的位置越高，估计精度越高，从图4和图5的结果可知这是因为低空目标的z坐标估计误差大。

5 结论

本文提出了利用两次ML估计的单站外辐射源TDOA定位算法。区别于多站定位，该单站定位模型采用多个外辐射源时差信息，该算法利用两次ML算法逐步解相关得到目标的精确位置。实验仿真采用6个外辐射源，并将估计的结果与CRLB对比，表明时差(TDOA)误差较小时，估计的均方误差(MSE)接近CRLB；随着目标远离观测站，x轴和y轴的估计结果越稳定，z轴估计误差越早偏离CRLB；通过作GDOP图可知，随着目标远离观测站，定位误差随之增大，距离增大到一定程度时达到极大值而后减小又增大的趋势，目标距离地面的高度越低，z轴的估计误差越大。该方法利用单站接收目标的多个信号时差信息进行定位，能够克服多站定位中时间同步困难等问题。

[1]Farina Alfonso, Kuschel Heiner. Guest editorial special issue on passive radar(Part I)[J]. IEEE Aerospace and Electronic Systems Magazine, 2012, 27(10): 5-5.

[2]Belfiori F, Monni S, Van Rossum W, et al. Antenna array characterization and signal processing for an FM radio-based passive coherent location radar system[J]. IET Radar Sonar & Navigation, 2012, 6(8): 687-696.

[3]Wang H, Wang J, Zhong L. Mismatched filter for analogue TV-based passive bistatic radar[J]. IET Radar Sonar & Navigation, 2011, 5(5): 573-581.

[4]Poullin D, Flecheux M. Passive 3D tracking of low altitude targets using DVB (SFN Broadcasters)[J]. IEEE Aerospace and Electronic Systems Magazine, 2012, 27(11): 36-41.

[5]Falcone P, Colone F, Lombardo P.Potentialities and Challenges of WiFi-Based Passive Radar[J]. IEEE Aerospace and Electronic Systems Magazine, 2012, 27(11): 15-26.

[6]Weiss A J. On the accuracy of a cellular location system based on RSS measurement[J]. IEEE Trans Veh Technol, 2003, 52(6): 1508-1518.

[7]Rong Peng, Sichitiu M L. Angle of arrival localization for wireless sensor networks[C]//Proc Int Conf Sensor and Ad Hoc Communications and Networks, Virginia, USA, 2008.

[8]WANG D, ZHANG L, WU Y. Constrained total least squares algorithm for passive location based on bearing-only measurements[J]. Science in China(Series F), 2007, 50(4): 576-586.

[9]Guvenc I,Chong Chia-Chin. A survey on TOA based wireless localization and NLOS mitigation techniques[J]. IEEE Commun Surveys & Tutorials, 2009, 11(3): 107-124.

[10]Yu H, Huang G, Gao J. Constrained total least-squares localization algorithm using time difference of arrival and frequency difference of arrival measurements with sensor location uncertainties[J]. IET Radar Sonar and Navigation, 2012, 6(9), 891-899.

[11]Shen J Y, Molisch Andreas F, Salmi Jussi. Accurate passive location estimation using TOA measurements[J]. IEEE Transaction on Wireless Communications, 2012, 11(6): 2182-2192.

[12]牟之英，刘博. 多平台对多目标无源融合定位方法[J]. 探测与控制学报，2017, 39(1):58-65.

[13]彭华峰, 曹金坤, 郑超. 同步卫星无源测轨中的时差定位与精度分析[J]. 系统工程与电子技术 2012, 34(11): 2219-2225.

Single-ObserverPassiveCoherentTDOALocationUsingTwiceMLEstimationAlgorithm

ZHANG Yuling1, HE Jun1, ZHU Jiandong2, DAI Huanyao2

(1.Shengda College of Economics & Trade Management of Zhengzhou, Zhengzhou 45119, China; 2.Electronic Equipment test Center, Luoyang 471003, China)

To solve the high complexity of multi-station passive coherent Location systems,the single-station location based on time difference of arrival is studied. two-step maximum likelihood (ML) estimation algorithm was iterated to get target position and distance estimation. The simulation showed that, when the time difference of arrival (TDOA) error was small, the estimated mean square error (MSE) was close to CRLB. Meanwhile, as the target was far from the observation station, the positioning error increases, and the lower the height of the target, the greater the estimation error ofz-axis. The proposed location method used time difference information of single-station to receive the multiple signal from a target, which could overcome those difficulties such as time synchronization in the multi-station locating.

single-station passive coherent Location; maximum likelihood; TDOA localization; CRLB

2017-04-26

国家自然科学青年基金项目资助(61401469)

张玉灵(1979—)，女，河南郑州人，硕士，副教授，研究方向：应用数学、雷达信号处理的理论和方法。E-mail:leoneast@sina.com。

TN974

A

1008-1194(2017)05-0045-07