高中数学“过程化”教学策略与实践研究
姜震羽


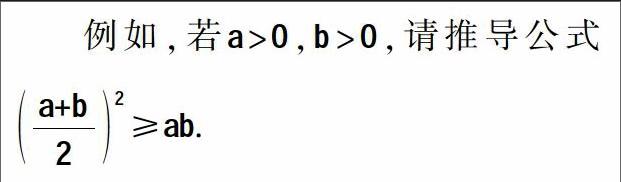
[摘 要] “过程与方法”目标是高中数学课程目标中的一个关键点,因此,教师在实际教学中应使教学活动的设计与目标保持一致. 具体的教学课堂活动就是教师引导学生进行概念、定义以及法则等体验的过程,数学知识在此过程中也会得到不断的探索与概括.
[关键词] 高中数学;过程与方法;优化策略
实现数学教学三维目标中“过程与方法”的目标必然应该重视教学的过程化,因此,本文结合具体的教学案例就教学过程的优化策略展开仔细的分析.
概念教学“过程化”
概念教学是高中数学教学中最为基本的内容之一,且具有十分重要的意义. 而数学概念教学中最为重要的实际上便是概念的形成,因此概念形成过程的理解与掌握也就成为概念教学的重心. 作为教师,单纯地让学生进行概念的记忆是不可取的,引领学生对概念进行推导并在此基础上对本来抽象化的概念进行不断深入与理解才是教师概念教学中正确的做法. 因此,对照三维目标中“过程与方法”目标的实现离不开数学概念教学的重点关注,尤其是概念形成过程的重点关注.
案例1:反比例函数的概念教学
首先教师应该将贴合实际的问题情境精心设计并引进反比例函数教学的课堂,让学生在感知与体验中理解反比例函数的定义:如果两个变量每一组对应值的乘积都不等于零,且该乘积为常数,我们便可以认定这两个变量之间成反比.
反比例函数的概念在初步明确以后,如果教师仍然特别机械地强化概念的本质,学生一味被动、机械地对概念加以记忆和生硬的理解,后续的学习将变成机械的重复,看似都是正常的教学活动,但这样的教学活动中学生的思考与体验基本是不存在的,解决实际问题时往往也不会应用. 上述案例的设计虽然不是特别复杂的内容,但其遵循了一定认知发展的规律,用部分有代表性的练习让学生从中得到概念的理解和巩固.如果教师再增添学生练习体验的交流与讨论,学生对反比例函数的领悟将从概念的本质上得到有效的提高. 我们也不难看出,具体到例证的有力支撑既是三维目标实施的目的,也是抽象数学概念教学中最需要遵循的教学原则.
规律教学的“过程化”
教师在高中数学教学过程中还需对探究性的“过程化”加以关注,这是培养学生推理能力的关键过程,其中包含结论、法则以及公式等规律性知识的学习和研究.
案例2:等差数列教学
设计1:
(3)巩固训练:根据已知条件,算出各Sn的值.
a1=5,d=2,n=10;a1=100,d=2,n=50;a1=14,d=1,n=35.
大部分教师在具体的教学活动中会根据以上的设计来开展教学活动,设计含量在这样的过程中是基本不存在的,因此,教师们往往会把公式训练作为课程重点进行强化,但是,这样的做法对于真正促进学生知识理解是没有效果的,即使产生部分的理解那也是比较片面的,很多时候,三维目标中的“知识与技能”目标是实现了,但是“过程与方法”目标却远远不能达成. 但是,如果这部分教师在教学活动的设计上稍加调整与改动,那么三维目标中要求实现的“过程与方法”这一目标也就在教学活动设计中得到真正体现了.
(2)根据已知条件,算出各Sn的值.
a1=5,d=2,n=10;a1=100,d=2,n=50;a1=14,d=1,n=35.
(3)引导学生思考:假设已知a1,d,n,那么Sn能求出吗?
这样的调整首先能让学生进行一系列的练习并建立一定的体验,推出公式也就变得水到渠成了. 这两种教学过程中虽然也有相同的步骤,但它们之间的区别也正是不同教學理念的体现.前者体现的仍然是以知识传授与灌输为主的传统教学理念,后者却是比较注重学生思考及自主能力培养的启发式教学理念. 学生在学习过程中宝贵的过程性体验自然是教师应该帮助学生实现的,但是教师仍然不能忽略教学中学生主动获取知识的启发和引导,教师应将“过程与方法”真正融入教学活动的每一个细节中以真正实现“过程与方法”的教学目标,并使得学生学习的主体地位得到真正的保障和发挥,这才是科学的现代教学理念 .因此,教师设计相应的达标活动固然是过程性目标的有效落实,但对定理、法则的分析、知识的探究以及结合重难点所进行的教学环节的创造性设计都是教师为“过程与方法”目标的实现而应关注并实践的.
习题教学的“过程化”
有效提高学生的数学思考自然离不开概念、公式、法则以及定理的教学,不过,最终能够体现学生解题时探究性思路的还是问题最终解决过程所表现出来的思路. 在不断发现问题与解决问题的特定教学环境中,学生对于相关概念、公式、法则以及定理的应用能力也会随之不断提高,因此,教师应该注重学生数学解题思路的锻炼与培养,否则要想实现“过程与方法”目标一定会存在较大的难度.
案例3:不等式的证明
相当一部分的教师会在实际教学中首先给出结论,然后请学生根据给出的答案再对公式进行证明,这样的做法看似为学生提供了简便的解决问题的方法和过程,但从实质上说来,具体的探究问题的过程却是学生没有经历也无法体验的,学生长期处于这样的教学中往往会越来越依赖教师,这是不应该出现的局面. 因此,教师在教学中一定要注意引导学生观点的自由发挥,让学生将自身正确的、错误的认识都能暴露在教师面前,只有这样,教师才能根据学生的认知体验进行有目的、有针对性的指导,这也正是学生主体地位得到重视的体现,以学定教的宗旨也在这个过程中体现了.
情感教学的“过程化”
学习兴趣、责任、生活态度以及人生态度等都是包含在情感态度和价值观目标体系中的,这里还对个人价值与社会价值的统一提出了具体的要求.这是无法在单单一节课上实现的隐性目标. 只有结合情感态度和价值观目标才能使得这些隐性目标得以实现.情感态度和价值观这两类人的主观思想其实是人对于社会或者其他人所表现出的主动反应. 这些建立在世界观与价值观基础之上的反应其实都是行为主体思想认识的主动选择,主体性认识是这些反应的行为基础. 这种情感的教育虽然属于价值观教育的范畴,但因其对今后个人的情感态度以及价值观认识并不会产生影响,因此这种教育变成有效情感态度教育的可能性基本是不存在的.
对他人的模仿以及个人的实践一般是学生个人成长过程中进行学习的有效选择. 学生学习的必经之路必然会有实现自身锻炼的实践、社会体验和群体生活这些内容. 在学校教育中,教师自然应该用自身积极的人生态度对学生的情感及价值观施以积极的影响,用自己身体力行的行为使学生获得言传身教的教育,学生因此而受到的情感教育也表现得更加真实可行. 同时,教师还应积极创造有意义的实践活动使得学生从中建立自身价值观的认知. 另外,学生还可以对学科教学中所包含的情感资源进行学习和社科体会,学生个性化情感和态度形成必然会有这样的经历.
教师在面对学生的情感态度和价值观的教育时,教育方式主要有两个方面的要点:(1)言传身教. 教师注重言传身教的同时,还应为学生尽量创造出适合情感和价值观学习的环境与条件,使得学生在耳濡目染以及教师的教诲中形成自身的情感与价值观目标;(2)与情感教育相关的教育资源的挖掘.只要教师用心挖掘就能发现与情感教育相关的教育资源其实有很多,教师再特别注意一下自身的角色扮演,那么对于学生情感与价值观的教育也就意义重大了. 比如,高中数学思维能力培养的同时往往还会有情感态度与价值观的教育渗透其中. 结合数学知识、思想与方法的情感教育的主要来源是与实践相互联系的唯物主义教育. 因此,教师对于学生的情感教育首先必须建立在教授书本知识的基础之上,然后再结合情感态度及价值观对教学目标的达成进行渗透以及深层次的拓展.
总之,高中数学教学不可灌输,而应注重细节化、过程化,要让学生能够充分体验到数学知识的形成过程及所学知识之间的联系,感受数学存在的科学以及文化价值,在过程化的学习过程中丰富知识,提升解决数学问题的能力,升华数学学习的正情感.endprint

