结合贝叶斯近似变换的冲突证据合成方法*
孟蕾,许爱强,刘家祺
(海军航空工程学院a.飞行器工程系;b.科研部;c.兵器科学与技术系,山东 烟台 264001)
☞综合保障性技术
结合贝叶斯近似变换的冲突证据合成方法*
孟蕾a,许爱强b,刘家祺c
(海军航空工程学院a.飞行器工程系;b.科研部;c.兵器科学与技术系,山东 烟台 264001)
为了解决D-S证据理论在处理冲突证据合成问题中存在的不足,改进了证据合成规则,提出了用该规则和贝叶斯近似变换相结合的证据合成方法。首先分析了封闭世界和开放世界假定中识别框架上认知集合间的转换关系,然后根据证据理论和贝叶斯近似变换的基本知识分析冲突产生的影响,最后根据原证据焦元交集和并集的基数关系改进了合成规则,并进行了实例验证。改进的合成规则能更好的保留原来的信息,而且通过与贝叶斯近似变换的结合减少了焦元的数量,结果表明该方法是一种准确有效的冲突证据合成方法。
D-S证据理论;贝叶斯近似变换;焦元;冲突证据;证据合成;基本概率分布(BPA)
0 引言
证据理论最初由Dempster提出,后来由Shafer推广并且形成理论体系,所以通常称作D-S证据理论。该理论是Bayes理论的推广,由于该理论的先验知识比概率理论更容易获得,且能处理很多不确定性问题,目前在信息融合、故障诊断和专家系统等领域得到了广泛的应用。但证据合成规则尚没有坚固的理论支撑,而且随着证据和其元素个数的增加,计算上存在着潜在的指数爆炸问题,所以其合理性和有效性还存在较大争议。近年来,很多学者对证据理论进行了有益的探索和研究[1]。研究主要分3类:第1类是解释证据理论,主要有上下概率解释、广义Bayes理论解释和随机集理论解释[2-3];第2类是改进证据理论,主要从合成规则和融合模型2个方面进行[4-10];第3类是简化计算,各种近似算法推进了证据理论的实际应用[11]。
1 识别框架上的认知集合
如果关于某个领域问题的集合Θ中的元素是两两互斥,并且是完备的,一般为了降低问题复杂度,集合Θ是有限集,相关命题都是集合Θ的子集,称集合Θ为识别框架。例如关于集合Θ={a,b,c,d}的一个命题~a∧c∨d可以用集合{c,d}来表示。集合论中集合的包含关系和表示命题的逻辑关系存在着对应关系,因此关于集合Θ={a,b,c,d}所有命题的层次关系如图1所示。

图1 识别框架上命题的层次结构Fig.1 Proposition of discernment frame
在假设这样一个识别框架Θ的基础上可以建立一个推理模型,信任构建在Θ和它的子命题上,对Θ的部分子命题的信任可能要多于另外一些命题。Θ是参考领域,也是讨论的全部内容。只有Θ中的命题才会被考虑,任何Θ中没有的命题都被认为是不可能发生的。
事实上认知过程远非想象的那么简单。首先需要构建集合KP(known possible),KP是那些已经知道的可能为真的命题,但也要考虑那些没有想到的尚且不知道的命题集UP(unknown proposition),还有已经知道是不可能发生的命题集KI(known impossible)。在像贝叶斯这样的传统方法里,UP是假设为空的,真命题必须只存在KP里,这是人们普遍接受的高度理想化的封闭世界假定[12]。
这3个集合的内容不单是对问题进行详细分析就能得到的,还和已经出现的证据有关。随着新证据的出现,命题在这3个认知集合之间重新分布,它们之间的转换关系如图2所示。
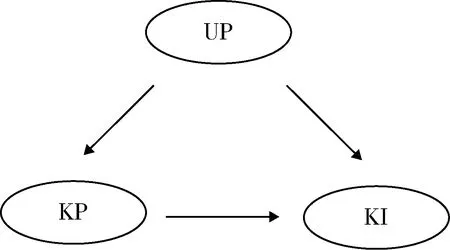
图2 认知集合之间的转换Fig.2 Transformation of cognitive sets
(1) 很容易理解,如果新出现的命题能充分证明A是不可能发生的,那么A从KP转移到集合KI。
(2) 如果新的证据提醒某些遗忘了的命题A是有可能为真时,那么A从集合UP转移到集合KP。
(3) 如果新的证据提醒某些遗忘了的命题A不可能发生时,那么A从集合UP转移到集合KI。但是这对已经建立在集合KP上的信任分布是没有实质影响的。
(4) 假设这3个集合事先对各个命题的划分都是正确的,真命题可能被分配到集合KP和UP中,而假命题也可能被正确的分配到KP,KI或者UP中。那么,命题A从KI到KP和从KP到UP的转移与这3个集合的定义是矛盾的。
真命题不可能分配到KI中,并且任何一个命题只要分配到KI中就只能呆在KI中不动,因此随着新证据的增加,KI中的命题的个数是单调增加的。KI中任何命题的信度都为0。随着新证据的增加,信度为0的命题KP转移到KI中。
封闭世界假定认为先验集合UP是空的,而开放世界假定承认存在着非空的集合UP,也承认真命题有可能存在于集合UP中。
按照前面的假设,真命题是永远不可能存在KI中的。但是考虑更一般化的假设,也可以接受真命题可能在KI中并且在所有的命题上构建一些变化信度函数来表示信度,这样每个命题都有可能属于这3个集合中的任何一个,在广义贝叶斯理论框架下发展出来的方法可以解决这样的问题。
2 重要概念梳理
2.1D-S证据理论
定义:集合Θ是一个识别框架,Θ上的一个基本概率分配(BPA)是一个函数m(·):2Θ→[0,1],其中2Θ是Θ的幂集,并且满足条件:

m(A)这个量叫做集合A的基本概率数,这个量只是集合A所代表的那个命题的信任度量,而一般情况下并不等于分配给集合A的所有信度,因为所有信度还包括集合A的子集所承担的那部分信度。下面这个定义很好的解释了这个问题。
定义:在识别框架Θ上由BPA函数m推导出来的信任函数Bel为

⊆Θ.
Bel(A)是分配给A的所有信度。每个信任函数Bel都是从一个特定的BPA函数m推导出来的,而BPA函数m又可以从信任函数Bel中恢复出来:
⊆Θ.
定义:函数m是信任函数Bel的基本概率分配。
(1) 如果m(A)>0,A叫做信任函数Bel的焦元;
(2)Bel的所有的焦元的集合叫做Bel的核;
(3) 如果Θ是唯一的焦元,称信任函数是空的;
(4) 如果所有的焦元都是单元素集合,Bel称为贝叶斯信任函数。
定义:识别框架Θ上2个基本概率分配函数m1和m2,分别导出信任函数Bel1和Bel2。如果
则称信任函数Bel1和Bel2是不可合成的,否则,通过Dempster合成规则就能合成BPA函数m1⊕m2,导出合成信任函数Bel1⊕Bel2。


能够运用上面合成规则的证据必须满足D-S独立的条件。D-S独立不同于概率论里面的独立,而是要求更为苛刻的一种独立条件。
2.2贝叶斯近似变换和广义信任函数
D-S证据理论在实际应用中往往受到指数爆炸问题的困扰,Voorbraak发现可以通过一种贝叶斯近似变换的方法减少焦元的个数,使其少于识别框架元素的个数[13]。
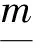
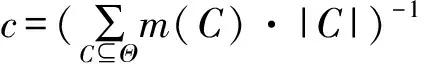
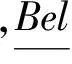
贝叶斯常数c被认为是对信任函数Bel给出信息的准确度和特殊性的度量,当c=|Θ|-1意味着最不精确的空信任函数,c=1说明信任函数最精确[13]。Dubois和Prade认为∑m(C)·|C|是可以用来衡量信任函数的不确定性的,因为∑m(C)·lb|C|代表不确定性。
贝叶斯近似变换和证据合成可以交换顺序:

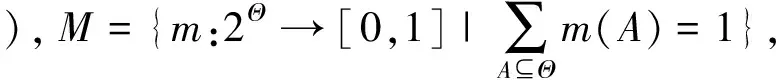
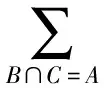
最早由Hummel和Landy提出空间(M,⊗),当时称其为“非正规化信任状态空间”,这在一定程度上平息了Zadeh对于Dempster合成规则处理高冲突证据合成的质疑。M中的元素m称为广义BPA函数。广义BPA函数导出的广义信任函数Bel:
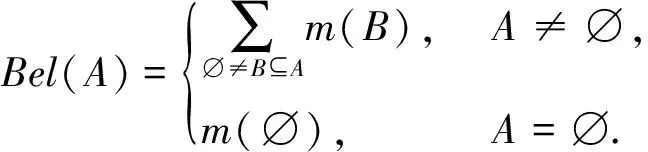
空间(M,⊗)是一个阿贝尔独异点。定义幺元:
m0(∅)=1;
m0(A)=0, ifA≠∅.
按照Dempster证据合成规则定义的正规化BPA函数空间(M,⊕),M中的元素m,g是(M,⊗)到(M,⊕)映射:
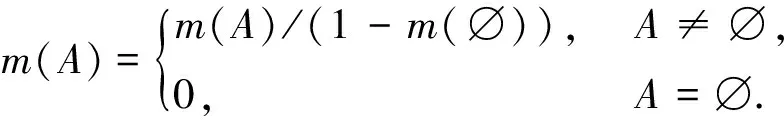


图3 3个空间之间的映射关系Fig.3 Map of three spaces
显然,g映射的作用是正规化,f映射的作用是进行贝叶斯近似变换。对证据合成后的结果正规化可能会使得贝叶斯常数减小,也就说信息的准确度有可能降低。因此,正规化因子的合理性一直存在着很大的争议。
3 新的冲突证据合成方法
3.1冲突证据的影响
在广义BPA函数空间(M,⊗)中处理有冲突的证据合成问题时,如果B∩C=∅,显然

也就是说2个证据中完全冲突的那部分信度被赋给了∅,Smets认为在开放世界假设中,∅的那部分信度代表集合UP中有真命题的可能性,即事实可能存在识别框架以外。
在正规化BPA函数空间(M,⊕)中,封闭世界假设认为识别框架肯定是完备的,无需考虑识别框架以外的情况,因此∅的信度被强制性的赋予零值[14]。也认为每一条证据都是完全可信的,因此只要有一条证据对命题A的基本概率分配为0,意味着命题A绝对不可能发生,那么命题A将被从认知集合KP中剔除到KI中,即使后来的证据完全支持A成立,也不可能再给命题A分配一点信度,这就是Dempster合成规则的一票否决问题[15]。
2种合成规则对Zadeh的经典冲突证据例子计算结果见表1。合成规则⊗将冲突信度0.999 9赋给了∅集,意思是真凶有极大可能性是A,B,C以外的第4人,并且排除了A,C的可能性。这样的结果有一定的合理性,但它打破了识别框架的完备性的限制,而且也没有解决一票否决的缺陷。
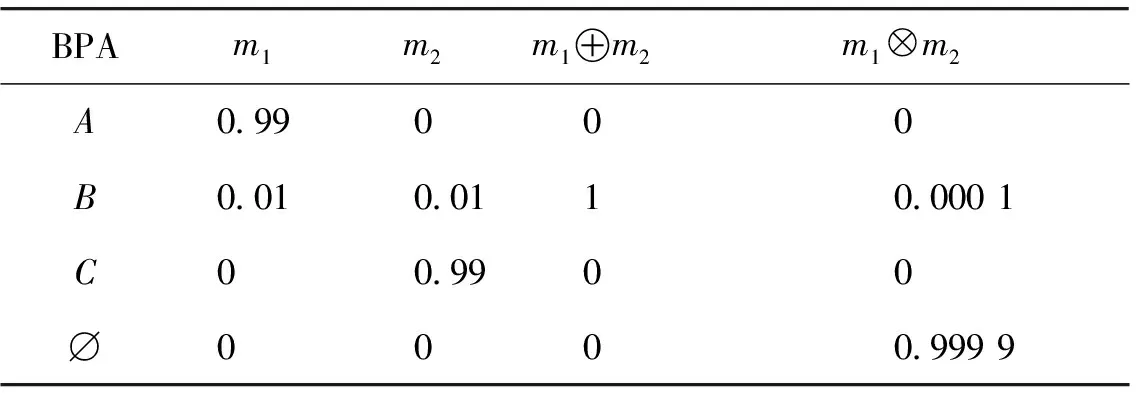
表1 证据合成规则⊕和⊗的结果Table 1 Combination results of ⊕ and ⊗
3.2新的冲突证据处理方法
Yager认为既然不知道冲突部分信度究竟该如何指派,就应该让它分布在所有的元素上,即赋予识别框架Θ:
m1⊥m2(∅)=0,
ifA≠∅,Θ,
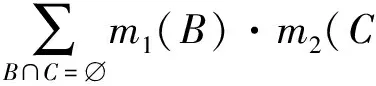
Yager的方法增加了证据合成结果的不确定性,Dubois和Prade提出了改进方法,如果2个证据源都是可靠的,信度应该赋给2个命题的交集;如果只有一个可靠,没有交集命题的信度该赋给并集:
∅)=0,



图4 B命题和C命题的关系Fig.4 Relationship of proposition B and C
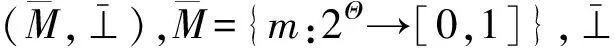
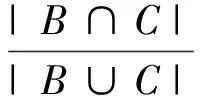
式中:|·|为集合的基数;k∩为一致因子,表示两个命题B和C的一致程度;k∪为冲突因子,表示命题B和C的冲突程度。

4 实例验证

表2 证据合成结果对比Table 2 Comparison of combination results
5 结束语
数值试验结果表明,在某些情况下对于证据源中非单点集BPA的变化,本文的合成规则克服了Dubois和Prade规则没有响应的缺点,因此能更好地保留合成之前证据源中的有用信息。
但是该方法继承了Dubois和Prade规则将冲突赋给并集的缺点,即合成后焦元个数可能会增加,从而使问题复杂化,而贝叶斯近似变换恰好能解决这个问题,并且能消除Dempster规则的一票否决缺陷,因此将这2种方法结合使用能达到理想的合成效果。
[1] 韩德强,杨艺,韩崇昭.DS证据理论研究进展及相关问题探讨[J].控制与决策,2014,29(1):1-11.
HAN De-qiang,YANG Yi,HAN Chong-zhao.Advances in DS Evidence Theory and Related Discussions[J].Control and Decision,2014,29(1):1-11.
[2] SHAFER G.Perspective on the Theory and Practice of Belief Functions[J].International Journal of Approximate Reasoning,1990(4):323-362.
[3] FIXSEN D,MAHLER P R S.The Modified Dempster Shafer Approach to Classification[J].IEEE Transactions on Systems,Man and Cybernetics,1997,27(1):27-41.
[4] ZADEH L A.Review of Shafer’s a Mathematical Theory of Evidence[J].AI Magazine,1984(5):81-83.
[5] YAGER R.On the Dempster-Shafer Framework and New Combination Rules[J].Information Sciences,1987,41(2):92-138.
[6] DUBOIS D,PRAD H.Consonant Approximations of Belief Functions[J].International Journal of Approximate Reasoning,1990(4):279-283.
[7] 孙全,叶秀清,顾伟康.一种新的基于证据理论的合成公式[J].电子学报,2000,28(8):117-119.
SUN Quan,YE Xiu-qing,GU Wei-kang.A New Combination Rules of Evidence Theory[J].Acta Electronica Sinica,2000,28(8):117-119.
[8] DENG Y,SHI W K,ZHU Z F,et al.Combining Belief Functions Based on Distance of Evidence[J].Decision Support Systems,2004,38(2):489- 493.
[9] 罗贺,尹艳平,胡笑旋.基于可信因子的证据源修正方法[J].系统工程与电子技术,2015,37(6):1459-1464.
LUO He,YIN Yan-ping,HU Xiao-xuan.Method to Modify Evidence Source Based on Trustworthy Factors[J].Systems Engineering and Electronics,2015,37(6):1459-1464.
[10] 刘哲席,阳建宏,杨德斌.基于信息总不确定度的冲突证据组合修正方法[J].电子与信息学报,2014,36(12):2909-2914.
LIU Zhe-xi,YANG Jian-hong,YANG De-bin.Combination of Conflicting Evidence by Using the Total Uncertainty Degree of Information[J].Journal of Electronics & Information Technology,2014,36(12):2909-2914.
[11] VOORBRAAK F.On the Justification of Dempster’s rule of Combination[J].Artificial Intelligence,1991,48(6):171-197.
[12] SMETS P,KENNES R.The Transferable Belief Model[J].Artificial Intelligence,1994,66(1):191-234.
[13] 徐凌宇,尹国成.基于不同信度的证据组合规则及应用[J].东北大学学报,2002,23(2):123-125.
XU Ling-yu,YIN Guo-cheng.Evidence Combination Rule Based on Different Reliability and Application[J].Journal of Northeastern University,2002,23(2):123-125.
[14] 罗志增,叶明.用证据理论实现相关信息的融合[J].电子与信息学报,2001,10(23):970-974.
LUO Zhi-zeng,YE Ming.Evidence Theory is Used to Implement the Information Fusion[J].Journal of Electronics and Information,2001,10(23):970-974.
[15] 戴冠中,潘泉,林辉.证据理论及其存在的问题[J].控制理论与应用,1999,16(4):465-469.
DAI Guan-zhong,PAN Quan,LIN Hui.Evidence Theory and Problems[J].Control Theory and Application,1999,16(4);465-469.
SyntheticMethodofConflictEvidenceCombinedwithBayesianApproximation
MENG Leia,XU Ai-qiangb,LIU Jia-qic
(Naval Aeronautical Engineering University,a.Airborne Vehicle Engineering Department; b.Scientific Research Department;c.Ordnance Science and Technology Department,Shandong Yantai 264001,China)
In order to solve the problems emerging in the situation trying to combine conflict evidences using Dempster-Shafer theory, a new combination rule based on Dubois and prade rule is put forward. A method of using the new rule together with Bayesian approximation is proposed to combine evidences from different bodies. Firstly the proposition transformation of discernment frame is discussed both in the open and closed world assumption. Secondly the effect of conflict is shown based on the Dempster-Shafer theory and Bayesian theorem. And finally the modified rule depending on the cardinal of set from different evidence bodies is proposed and is shown in the numerical example. Conclusion can be drawn from the example that the new combination rule reserves more information from the combined evidences and Bayesian Approximation reduces the number of focused elements, and using both of them is an effective and accurate method in evidence combination.
Dempster-Shafer theory; Bayesian approximation transformation; focal element; conflict evidence; evidence synthesis; basic probability assignment (BPA)
2016-09-21;
2016-11-21
中国博士后科学基金资助项目(2013M542535)
孟蕾(1987-),女,山东聊城人。讲师,博士,研究方向为装备保障预测和状态评估。
通信地址:264001 山东省烟台市芝罘区二马路188号航院504教研室E-mail:735546262@qq.com
10.3969/j.issn.1009-086x.2017.05.024
TJ760.7;O212.8
A
1009-086X(2017)-05-0149-06
——基于体育核心期刊论文(2010—2018年)的系统分析

