近程防空导弹发动机推力方案优化研究*

周梦琦，薛林，闫晓勇

(1.北京电子工程总体研究所，北京 100854；2.中国航天科工集团 第二研究院，北京 100854)

近程防空导弹发动机推力方案优化研究*

周梦琦1，薛林2，闫晓勇1

(1.北京电子工程总体研究所，北京 100854；2.中国航天科工集团 第二研究院，北京 100854)

以近程防空导弹为背景，探讨了双脉冲推进技术对导弹性能的提升效果。建立了飞行弹道的数学模型，给出了制导方法及推力模型，借用遗传优化算法，以扩大导弹近界至远界各典型弹道的末速度为优化目标，对各种推力方案下推力参数进行了优化。研究表明，相比于传统单级推力形式，双脉冲推力对近程导弹末速度提升明显；优化得到了使导弹末端机动性能最优的双脉冲推力方案，为近程防空导弹双脉冲发动机的设计提供了理论依据。

近程导弹；防空导弹；推力方案；双脉冲推力；末端速度；遗传算法

0 引言

在现代防御作战中，常根据杀伤距离的远近将防空导弹分为远程防空导弹、中程防空导弹和近程防空导弹。远程防空导弹负责在100～150 km的射程范围内拦截目标，中程防空导弹负责在20～100 km内拦截目标，近程防空导弹负责在20 km射程范围内拦截目标。

近年来，空袭作战的形式日趋复杂。为应对越来越多样化的空袭作战，有效保障地面目标的安全，中/远/近程防空导弹的射程界限日益模糊。近程防空导弹的射程从20 km扩展到30 km[1]，与中程防空导弹射程的重合区域扩大。

近程防空导弹为保障发射单元火力密集需限制弹径和发射质量；为保障拦截能力需具有较高的弹道末速；而增程需求进一步提升了设计难度。

本文认为，近程增程防空导弹总体设计的关键在于能否合理选择动力方案，在发动机总能量受限的情况下结合弹道的特点合理分配能量使其满足设计需求。因此，首先列出近程防空导弹的导引模型和发动机模型；然后给出多条典型弹道；接下来选取目标函数，应用遗传优化算法对采用单级推力方案、二级推力方案、双脉冲推力方案的中近程导弹分别进行优化；最后，通过对比说明双脉冲推力方案对增程近程防空导弹最为适用。

近程防空导弹在拓展射程的同时需要进行小型化设计，为了保障机动效能又要提高弹道末速，这就给总体设计带来一定难度。在总能量被限定的情况下，如何兼顾导弹小型化设计与总体性能，是总体设计需要解决的一个重要问题，本文从动力方案角度来考虑这一问题。

导弹动力方案主要分为以下几种：瑞士与美国共同研制的阿达茨、意大利的斯帕达等使用的单级推力方案；法国研制的麦卡、俄罗斯的根弗使用的双级推力方案；德国的LFK-NG等使用的双脉冲推力方案[2-3]。

由于双脉冲固体火箭发动机技术在提高导弹飞行性能方面的特点[4-5]，国外很早就对此展开了理论研究与地面试验[6-9]，也已经有比较成熟的武器成果。我国过去在这一领域的研究重点集中在远程及空空导弹[10-13]，在近程导弹方面的研究还很有限。为了进一步提高近程防空导弹的末端机动性，可使用具有能量可控特性的双脉冲固体火箭发动机替换传统单级推力发动机，来解决已有近程导弹型号潜力挖掘逐渐面临瓶颈的问题。

1 近程防空导弹的数学模型

本文研究工作的目标在于进行双脉冲发动机能量分配优化设计，考核发动机性能的指标为导弹末速度，由导弹飞行弹道模型计算得出[14]。

1.1导引模型

近程防空导弹的制导分为2个阶段：第1个阶段采用抛物线导引，通过速度追踪保证导弹速度矢量方向始终沿抛物线切向方向，最大限度的减小飞行攻角降低诱导阻力以保留能量；第2个阶段，在弹目相对距离≤8 km的情况下，采用比例导引，保证制导精度。

对于抛物线制导段，在飞行任意时刻可由导弹坐标(xm,ym)、期望的落点坐标(xA,yA)以及期望的落角εt决定唯一的一条抛物线，如图1所示。

图1 抛物线制导原理图Fig.1 Schematic diagram of parabolic guidance

可以得到弹-目运动方程组为

(1)

由此可推算得出，导弹所处位置的抛物线切线方向决定的期望弹道倾角为

(2)

式中：期望落点坐标(xA,yA)由导弹与目标的运动参数实时计算得出。导弹的升降舵偏转角δz为

δz=kθ(θ-θt)，

(3)

式中：kθ为放大系数；θ为导弹的瞬时弹道倾角。

弹道高度对导弹末速度影响突出，弹道高度越大，导弹受气动阻力影响所造成的速度衰减越小。在本文中，导弹弹道高度主要取决于抛物线制导段所设置的期望落角，期望落角越大，导弹的弹道高度越高。为避免影响交班及末制导，落角限制在20°～30°，仿真过程设置期望落角为限制内最大值30°。

比例导引段的控制由法向过载ay提供

(4)

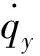
1.2发动机模型

发动机模型给出导弹动力参数，传统单级推力发动机模型给出的推力参数包括推力大小F及工作时间t。

双级推力及双脉冲模型参考图2，双脉冲推力模型参数包括发动机第1，2次工作推力F1，F2；发动机第1，2次工作时间t1，t2；发动机2次工作的时间间隔Δt；双级推力模型的时间间隔为0。

图2 两次点火发动机推力图谱Fig.2 Propulsion map of dual ignition engine

本文以某型号近程防空导弹为模型背景，在导弹总体对发动机尺寸和质量都进行限定的情况下，双脉冲发动机的总能量及推进剂质量也是确定的。在文中取双脉冲发动机总冲为275 kN·s，发动机总推进剂质量为100 kg。

1.3导弹打击目标

针对近程防空的特点，认为导弹的打击目标主要为有人驾驶飞机。基于此，本文设定打击目标为在空中1～12 km高处以匀速300 m/s直线接近的质点目标，射程从近界至远界为15～30 km(实际命中点根据导弹发动机推力、制导控制等方案影响有所浮动)。仿真5条典型弹道，分别打击30，25，20，15 km远，1 km高目标和30 km远，12 km高目标。

2 优化模型建立

2.1目标函数

防空导弹在击中目标前的瞬时速度称为末速度，它在很大程度上决定了导弹在打击目标时的机动性能，是衡量防空导弹性能的一项具有实战意义的重要参数，本文以导弹的末速度作为进行双脉冲发动机优化的目标函数。

在针对高空目标时，由于气动阻力对导弹速度的衰减影响小，末速度较低空目标相比高出很多，因此在做目标函数时只考虑低空目标。

(1) 单级推力

图3给出了导弹在相同单级推力下，针对4种典型低空机动目标的飞行速度。

图3 导弹在单级推力下的飞行速度Fig.3 Velocity of missile with single-stage propulsion

仿真结果表明，打击低远目标时，导弹末速度较低，从远界至近界末速度约为280～570 m/s。更多考虑远界弹道情况，则目标函数为

S=5v1+2.5v2+1.5v3+0.5v4，

(5)

式中：v1，v2，v3，v4分别表示射程为30，25，20，15 km远弹道末速度。

(2) 双级推力

图4给出了导弹在相同双级推力下，针对4种典型低空机动目标的飞行速度。

图4 导弹在双级推力下的飞行速度Fig.4 Velocity of missile with dual-stage propulsion

导弹在打击30 km远，1 km高和25 km远，1 km高目标时，末速度约为310 m/s和400 m/s；而在打击近界目标时，末速度则能达到600 m/s以上。更多考虑远界弹道情况，则目标函数为

S=3v1+v2.

(6)

(3) 双脉冲

图5给出了导弹在相同双脉冲推力参数下针对4种典型低空机动目标的飞行速度。

图5 导弹在双脉冲推力下的飞行速度Fig.5 Velocity of missile with dual pulse propulsion

导弹在打击30 km远，1 km高和25 km远，1 km高目标时，末速度约为350 m/s和500 m/s；而在打击近界目标时，末速度则能达到750 m/s以上。更多考虑远界弹道情况，则目标函数为

S=5.7v1+v2.

(7)

在优化过程中，适应度值S均为无量纲参数。

2.2优化变量及取值范围

对于单级推力模型，为确保优化结果具有实际工程意义，在发动机总冲及推进剂质量确定的条件下，对发动机参数提出以下限制条件：①导弹发动机燃料总质量mp不变；②发动机燃料的总冲I总不变，即

mp=100 kg，

(8)

I总=F(t)t=275 kN·s.

(9)

优化变量为发动机工作推力大小F(取值范围为30～40 kN)，工作时间t由公式(9)计算得出。

对于双级推力和双脉冲模型，增加以下发动机限制条件：①发动机工作总时间限定在一定范围内；②发动机2次工作推力大小之比小于4(为简化模型本文中取3.98)；③双脉冲时间间隔Δt变化范围在0～20 s之间，即

18≤t1+t2≤24，

(10)

F1/F2=3.98，

(11)

0≤Δt≤20.

(12)

优化变量为发动机第1次工作推力F1(取值范围为30～40 kN)，第1次工作时间t1(取值范围为2.5～5 s)及发动机2次工作的时间间隔Δt(取值范围为0～20 s，在双级推力模型优化中取值为0)。发动机第2次工作时间t2及推力F2由条件公式(9)和(11)计算得出。

2.3遗传优化算法

遗传算法是一种基于生物遗传和进化机制的自适应概率优化技术，它对优化问题的控制变量进行编码后，模仿生物基因在遗传过程中的复制、交叉、变异等行为，通过遗传变异得出最终优化结果，是当前解决复杂系统优化问题的一种较为实用的方法。本文在优化模型时采用Matlab应用程序中的遗传算法工具箱[15]，在工具箱中默认最优适应度值为最小值，所以在优化过程中取适应度函数为目标函数的负数值。

3 优化过程和结果分析

3.1发动机优化过程及结果

(1) 单级推力

单级推力发动机目标函数的进化过程如图6所示。

图6 单级推力目标函数进化过程Fig.6 Evolutionary process of objective function with single-stage propulsion

在单级推力优化过程中，经过遗传进化目标函数的平均值在第51代时收敛于当前子代的最佳值。此时，得到的最佳推力为30 kN，发动机工作时间为8.95 s。

(2) 双级推力

双级推力发动机目标函数的进化过程如图7所示。

图7 双级推力目标函数进化过程Fig.7 Evolutionary process of objective function with dual-stage propulsion

在双级推力优化过程中，目标函数的平均值在第51代时收敛于当前子代的最佳值。此时，得到的发动机推力参数如表1所示。

表1 双级推力优化方案Table 1 Optimization scheme of dual-stage propulsion

(3) 双脉冲

双脉冲发动机目标函数的进化过程如图8所示。

图8 双脉冲目标函数进化过程Fig.8 Evolutionary process of objective function with dual pulse propulsion

在双脉冲优化过程中，目标函数的平均值在第71代时收敛于当前子代的最佳值。此时，得到的双脉冲参数如表2所示。

3.2优化结果分析

通过优化，得到了使导弹在各推力方案下综合末速度达到最大的推力参数。使用各方案发动机推力优化结果，对各典型弹道进行仿真，并在双脉冲方案中优化间隔时间，结果如表3所示。

表2 双脉冲推力优化方案Table 2 Optimization scheme of dual pulse propulsion

表3 各推力方案优化下导弹末速度Table 3 Optimal terminal velocity with differentpropulsion schemes (m·s-1)

其中，使用双脉冲模型在打击15 km远，1 km高目标时的最优脉冲间隔Δt为5 s，一旦延长则导弹在击中目标时发动机内燃料没有完全消耗；其他典型弹道的最优脉冲间隔均为20 s。

由表3可以看出，采用双脉冲发动机后，导弹在打击目标前的末端速度得到了显著提升，从而使得导弹获得了更好的末端机动性能。

以上仿真结果验证了遗传算法对双脉冲导弹的推力优化的有效性，证实了双脉冲推进技术在提高近程防空导弹综合性能上的显著能力。

4 结论

本文结合近程防空导弹的特点，通过优化不同弹道及不同推力方案下的导弹性能，对比分析双脉冲推力模式对近程防空导弹弹道性能的影响。仿真结果表明：

(1) 双脉冲推力形式能够有效提高导弹在击中目标前的瞬时速度，进而提高导弹机动能力，从而增强对目标的打击能力。

(2) 针对本文采用的近程防空导弹模型，在结合工程实际给出的发动机模型条件下，得出了在各动力方案下的最优推力组合，并给出了在双脉冲模型下各弹道的最佳脉冲间隔，为近程防空导弹双脉冲发动机的设计提供了理论依据。

[1] 成楚之.近程防空中的国土防空与野战防空[J].现代防御技术,2007,35(6):1-6.

CHENG Chu-zhi.National Air Defense and Battlefield Air Defense in Short-Range Air Defense[J].Modern Defence Technology，2007,35(6):1-6.

[2] NAUMANN KW，STADLER L，TROUILLOT P，et al.Double-Pulse Solid Rocket Technology at Bayern-Chemie/Protac[R].AIAA 2006-4761.

[3] STADLER L J，TROUILLOT P，RIENACKER C，et al.The Dual Pulse Motor for LFK NG[R].AIAA 2006-4726.

[4] 龚世杰,戴耀松.多脉冲固体火箭发动机述评[J].飞航导弹,1993(1):32-39.

GONG Shi-jie，DAI Yao-song.Review of Multi-Pulse Solid Rocket Motors[J].Winged Missiles Journal，1993(1):32-39.

[5] 刘廷国,何洪庆.多脉冲能量控制在战术导弹中的作用[J].推进技术,1998,19(5):110-114.

LIU Ting-guo，HE Hong-qing.Investigation of Application of Multi-Pulse Energy Control Technology to Tactical Missiles[J].Journal of Propulsion Technology,1998,19(5):110-114.

[6] JONES R A，MABRY M W.Barrier System for Dual-Pulse Rocket Motor[P].United States Patent,4085584,1978.

[7] CARRIER J L C，CONSTANTINOU T，SHEA C J，et al.Solid Rocket Motor with Dual Interrupted Thrust：US，US4972673[P].1990.

[8] SCHILLING S，TROUILLOT P，WEIGAND A.On the Development and Testing of a 120 mm Calibre Double Pulse Motor (DPM)[R].AIAA 2004-3387.

[9] PHILIPS C.Energy Management for Multiple-Pulse Missiles[J].Journal of Spacecraft & Rockets，1990,27(6):623-629.

[10] 张弫,成楚之,于本水.多次点火固体火箭发动机在面空导弹上的应用研究[J].现代防御技术,2001,29(5):31-33.

ZHANG Zhen，CHENG Chu-zhi，YU Ben-shui.Research of the Application of Air Defense Missile with Multi-Pulse Solid Rocket Motor[J].Modern Defence Technology,2001,29(5):31-33.

[11] 张弫,郑时镜,于本水.遗传算法在远程防空导弹总体优化设计中的应用[J].系统工程与电子技术,2003,25(1):34-37,60.

ZHANG Zhen，ZHENG Shi-jing，YU Ben-shui.Application of the Genetic Algorithms in the Optimization Design of the Long-Range Air Defense Missile System[J].Systems Engineering and Electronics,2003,25(1):34-37,60.

[12] 程仙垒,彭双春,郑伟,等.多约束条件下非连续助推弹道方案设计与优化[J].系统工程与电子技术,2015,37(4):888-894.

CHENG Xian-lei，PENG Shuang-chun，ZHENG Wei，et al.Design and Optimization of Non-Continuous Boost Trajectory under Multi-Constrains[J].Systems Engineering and Electronics,2015,37(4):888-894.

[13] 王志健,何国强,魏祥庚,等.空空导弹多脉冲固体火箭发动机能量分配优化研究[J].弹箭与制导学报,2010,30(6):144-146.

WANG Zhi-jian，HE Guo-qiang，WEI Xiang-geng，et al.Energy Allocation Optimization of Multi-Pulse Solid Rocket Motor for Air-to-Air Missile[J].Journal of Projectiles，Rocket，Missiles and Guidance,2010,30(6):144-146.

[14] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京：北京理工大学出版社,2015:2-48.

QIAN Xing-fang，LIN Rui-xiong，ZHAO Yan-nan.Dynamics of Flight for Missiles[M].Beijing：Beijing Institute of Technology Press,2015:2-48.

[15] 雷英杰，张善文.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社,2014:1-2.

LEI Ying-jie，ZHANG Shan-wen.MATLAB Genetic Alorithem Toolbox and Its Application[M].Xi’an：Xidian University Press,2014:1-2.

OptimizingMotorPropulsionSchemeinShortRangeAntiaircraftMissiles

ZHOU Meng-qi1，XUE Lin2，YAN Xiao-yong1

(1.Beijing Institute of Electronic System Engineering，Beijing 100854，China；2.The Second Research Academy of CASIC，Beijing 100854，China)

Based on short range antiaircraft missiles, the enhancement effect of dual pulse propulsion technology for missile performance is studied. The mathematical model of flight trajectory, guidance and thrust are built. Aiming at promoting the terminal velocity, the performance parameters of the engine with different propulsion schemes are optimized by genetic algorithm for each typical trajectory from near edge to far edge. According to the optimization, the terminal velocity of short range missiles is promoted more markedly by dual pulse propulsion than by traditional single stage propulsion; the optimal dual pulse thrust scheme of terminal maneuvering performance has been acquired. These results offer theoretical evidence for the design of dual pulse motor in short range antiaircraft missiles.

short range missiles；antiaircraft missiles；thrust scheme；dual pulse thrust；terminal velocity；genetic algorithm

2016-12-03；

2017-02-06

有

周梦琦(1992-)，女，辽宁旅顺人。硕士生，主要研究方向为飞行器总体设计。

通信地址：100854 北京市142信箱30分箱E-mail：879533710@qq.com

10.3969/j.issn.1009-086x.2017.05.008

TJ761.1+3;TJ765.1

A

1009-086X(2017)-05-0042-06