通用的雷达目标RCS统计建模方法*

张晨新，林存坤，周成，宗彬锋，丁德文

(1.空军工程大学 防空反导学院，陕西 西安 710051；2.中国人民解放军95972部队，甘肃 酒泉 735018； 3.空军装备研究院通信所，北京 100085；4.中国人民解放军94710部队，江苏 无锡 214000； 5.中国人民解放军94259部队，山东 蓬莱 265600)

☞探测跟踪技术

通用的雷达目标RCS统计建模方法*

张晨新1，林存坤2，周成3，宗彬锋4，丁德文5

(1.空军工程大学 防空反导学院，陕西 西安 710051；2.中国人民解放军95972部队，甘肃 酒泉 735018； 3.空军装备研究院通信所，北京 100085；4.中国人民解放军94710部队，江苏 无锡 214000； 5.中国人民解放军94259部队，山东 蓬莱 265600)

针对传统的雷达目标RCS起伏统计模型都是基于厘米波频段RCS建立的问题，提出了一种更为通用的基于混合正态分布的RCS统计建模方法。对典型隐身飞机的仿真数据和某型教练机的实测数据进行统计分析，拟合优度检验结果表明：混合正态分布在米波频段和厘米波频段均能实现最佳的拟合优度。研究成果可用于拓展雷达检测理论，为雷达总体设计提供理论支撑。

雷达目标；雷达散射截面；RCS起伏模型；统计建模；混合正态分布；拟合优度检验

0 引言

雷达散射截面(radar cross section，RCS)作为回波信息的重要组成部分，反映雷达目标对照射电磁波的散射能力，在雷达检测领域有着广泛的应用。RCS与照射电磁波的频率、极化，目标相对于雷达的姿态和目标本身的特性有关，因此，RCS幅值总是随时间或者姿态角呈现无规律起伏，因此普遍采用统计建模方法来分析RCS的起伏特性[1]。雷达目标的RCS起伏特性可以预测雷达的检测性能和评估飞机的散射特性。

20世纪60年代，Swerling首先用Swerling起伏模型来描述回波起伏损耗对雷达检测性能的影响[2]，后来，他将Swerling模型发展成更为通用的卡方分布模型，这一结论由于高度的军事敏感性直到20世纪90年代才公布[3]。之后，学者们又相继提出了赖斯分布和对数正态分布等，这些模型至今仍然被广泛地应用[4-7]。与此同时，更精确的RCS起伏模型相继提出，黄培康等人提出了非参数法模型，采用勒让德多项式对概率密度函数曲线进行拟合，可以实现很好的拟合精度[4]。文献[7]针对隐形飞机RCS可能出现平均中值比小于1的情况，提出了对数正态分布的完备形式，与传统的对数正态分布相比表现出了优越性。文献[8]将常用于杂波统计描述的韦布尔分布与SwerlingⅠ，Ⅲ型分布和对数正态分布进行等效分析，韦布尔分布在锥体和飞机目标的RCS统计分析中均取得最优拟合效果。文献[9]采用3种分布模型系统地研究了不同航迹的动态RCS分布特性。文献[10]则是应用3种起伏模型对不同的典型隐身飞机静态RCS的起伏统计特性开展了系统研究。徐振海等人提出一套完整的选择隐身目标RCS最优分布模型的方法[11]。

当研究对象为隐身目标时，分析隐身目标的米波段RCS对反隐身作战应用具有重要意义。而公开文献中的研究都是针对厘米波频段的RCS进行统计分析，因此本文提出了适用于米波频段和厘米波频段的基于混合正态分布的通用统计建模方法，并用某型教练机实测RCS数据验证了混合正态分布的优越性。

1 RCS的起伏统计模型

1.1卡方分布

卡方统计模型是在Swerling模型的基础上提出来的[3]，它的概率密度函数(PDF)表示为

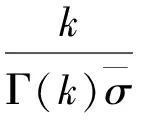
(1)

1.2对数正态分布

对数正态分布[6]常用来描述由不规则外形散射体组合的电大尺寸目标，其概率密度函数表示为

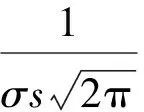
(2)

式中：σ为RCS值；μ和s分别为均值和标准差。正态分布和对数正态分布是紧密联系的，当变量σ满足参数为μ和s的对数正态分布时，则变量lnσ满足参数为μ和s的正态分布。需要说明一点，对数正态分布还有一种以平均中值比ρ和中值σ0为参数的表现形式，这两者的本质是等效的。

1.3混合正态分布

混合正态分布(Gaussian mixture distribution)已广泛地应用于图像处理和语音识别等领域，它的一个重要特性是，当模型中分量足够多时，它能够以任意精度逼近任意分布[12]。因此，本文考虑将该分布应用于RCS的统计分析以达到精确建模的目的。

混合正态分布的概率密度函数表达式为

(3)

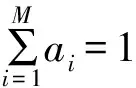
2 隐身飞机RCS 的分析

2.1研究对象

建立的隐身目标CAD模型和姿态角定义如图1所示。机体坐标系原点位于目标质心，xb轴平行于机身纵轴指向机头，zb轴位于机身对称平面内，垂直于xb轴向上，yb轴垂直于目标对称平面，指向由右手法则确定。方位角φ为雷达视线在Oxbyb平面的投影与Oxb轴的夹角，向yb轴方向为正，φ∈[-180°,180°]。俯仰角θ为雷达视线在Oxbzb平面的投影与Oxb轴的夹角,向上为正，θ∈[-90°,90°]。

图1 隐身目标模型和机体坐标定义Fig.1 Stealth target model and definition of target coordinate

2.2目标RCS的计算

将建立的目标CAD模型导入到电磁场仿真软件FEKO中，并选用多层快速多极子算法(multilevel fast multipole method，MLFMM)进行计算目标全空域的静态RCS特性[13]。MLFMM算法是精确求解电大尺寸问题最为有效的方法，FEKO作为世界上第一个把MLFMM推向市场的三维全波电磁仿真软件，在计算电大尺寸目标的RCS方面具有明显的优势。适用的雷达频段涵盖了常见的微波雷达工作频段，因此可用于计算雷达目标对应的雷达散射截面。

作战过程中，巡航和突防是最重要的2个过程，巡航时，飞机一般做侧站平飞运动；突防过程中，头向是威胁最大的方向[14]。因此，本文仿真了VHF频段垂直极化鼻锥方向(-15°≤φ≤15°,-15°≤θ≤15°)、机身侧向(75°≤φ≤105°,-15°≤θ≤15°)L频段垂直极化鼻锥方向(-15°≤φ≤15°,-15°≤θ≤15°)的局部区域RCS。

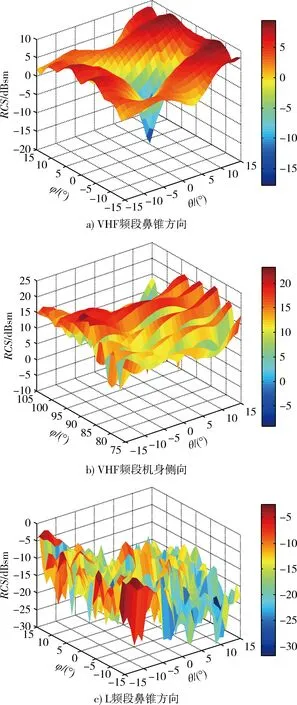
图2 隐身飞机局部区域的RCSFig.2 Static RCS of partial region of stealth aircraft

由图2可以看出，在鼻锥方向时，L频段的RCS均低于0 dBsm(1m2)，而VHF频段的大部分RCS 均处于0 dBsm上方，可见米波段的RCS明显高于厘米波段的RCS，因此米波雷达具有高效的反隐身效果。为定量比较频率和姿态角范围对RCS的影响，表1给出了图2中局部区域RCS的统计参数信息。由表可得，鼻锥方向L频段 的RCS均值约为0.06 m2，机身侧向的RCS明显高于鼻锥方向的RCS，符合实际情况。

为了验证所提混合正态分布建模方法的有效性，本文用某型教练机的实测动态RCS数据进行验证。测量参数为C频段垂直极化，飞行航迹为侧站平飞，动态RCS如图3所示。

表1 RCS的统计参数Table 1 Statistical parameters of RCS m2

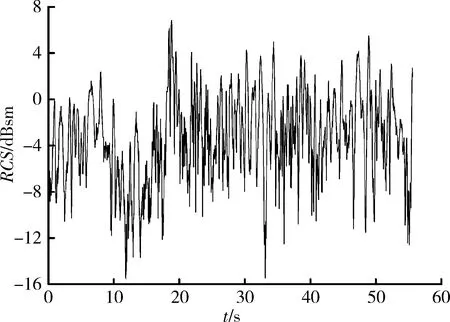
图3 某型教练机的实测动态RCSFig.3 Measured dynamic RCS of one training plane

2.3RCS的拟合与检验

本节对1.2节中的RCS数据的概率密度进行研究。基于非线性最小二乘原则，分别应用卡方分布、对数正态分布、二阶混合正态分布进行拟合。图4分别给出了4类RCS的拟合结果，并采用非参数检验方法对拟合结果进行了拟合优度检验。

可直观地从图4得出，混合正态分布在VHF频段的拟合效果明显优于传统的起伏统计模型，而在L频段和实测RCS的拟合效果与传统起伏模型相当。为了比较3种分布模型对概率密度函数的拟合效果，采用Kolmogorov-Smirnov (K-S)拟合优度检验方法对拟合效果进行分析比较[15]。

K-S检验公式为

D=max|F(x)-F′(x)|，

(4)

式中：F(x)为样本数据的累积概率函数；F′(x)为统计模型的累积概率函数。D值越小表示模型与样本分布拟合得越好，比较D值大小反映出模型对RCS数据的拟合精度。K-S检验结果见表2。

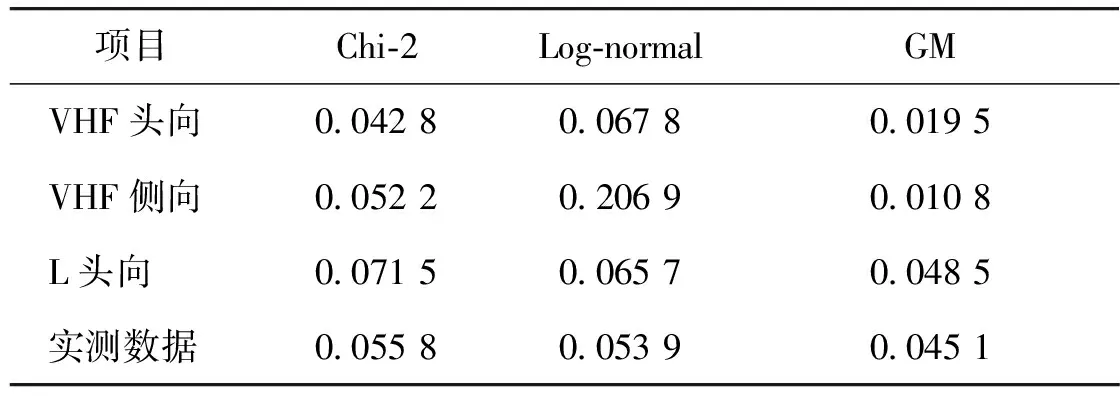
表2 K-S检验结果Table 2 K-S test result

图4 RCS概率密度函数的拟合结果Fig.4 Fitting result of RCS probability density funtion

由表2可知，在4类RCS的统计分析中，混合正态分布的D值均为最小，说明混合正态分布能够实现更高的拟合精度。尤其在VHF频段处表现出的优越性尤为明显，对于L频段和实测的RCS，混合正态分布的优势不大，这是因为传统的起伏模型都是基于实测数据建立，而实测数据亦是在微波频段测得，因此混合正态分布在微波频度的优势不明显。

3 结束语

无论隐身技术如何发展，雷达作为信息化作战条件下检测跟踪目标的主要手段不会改变。雷达工程师需根据反隐身技术发展的需要，对经典的雷达理论进行拓展修正便可继续应用。

本文提出了基于混合正态分布的RCS统计建模方法。通过对典型隐身目标的VHF频段RCS、L频段RCS以及某型教练机的实测RCS进行统计分析，该方法均能实现最佳的拟合优度。本文研究成果为反隐身技术发展和雷达系统仿真提供理论支持和仿真依据。

[1] 黄培康，殷红成，许小剑.雷达目标特性[M].北京：电子工业出版社，2005.

HUANG Pei-kang，YIN Hong-cheng，XU Xiao-jian.Radar Target Characteristic[M].Beijing：Publishing House of Electronics Industry，2005.

[2] SWERLING P.Probability of Detection for Fluctuating Target[J].IRE Transaction on Information，1960(6)：269-308.

[3] SWERLING P.Radar Probability of Detection for Some Additional Fluctuating Target Cases[J].IEEE Transactions on Aerospace and Electronic Systems，1997，33(2)：698-709.

[4] XU X J，HUANG P K.A New RCS Statistical Model of Radar Target[J].IEEE Transactions on Aerospace and Electronic Systems，1997，33(2)：710-714.

[5] 张伟，王国玉，曾勇虎.飞机目标动态RCS分布特性研究[J].电波科学学报，2010，25(1)：118-121.

ZHANG Wei，WANG Guo-yu，ZENG Yong-hu.Distribution Characteristic of Airplane Dynamic RCS[J].Chinese Journal of Radio Science，2010，25(1)：118-121.

[6] SHI W Q，SHI X W，XU L.RCS Characterization of Stealth Target Usingχ2Distribution and Lognormal Distribution[J].Progress in Electromagnetics Research M，2012，27，1-10.

[7] 史伟强，徐乐，史小卫，等.基于完备对数正态分布模型的隐形飞行器动态RCS统计特性研究[J].电子与信息学报，2013，35(9)：2121-2125.

SHI Wei-qiang，XU Le，SHI Xiao-wei，et al.Dynamic RCS Statistic Characterization of Stealth Aircraft Using Complete Lognormal Distribution[J].Journal of Electronics & Information Technology，2013，35(9)：2121-2125.

[8] SHI W Q，SHI X W，XU L.Radar Cross Section(RCS) Statistical Characterization Using Weibull Distribution[J].Microwave and Optical Technology Letters，2013，55(6):1355-1358.

[9] 庄亚强，张晨新，张小宽，等.典型隐身飞机动态RCS仿真及统计分析[J].微波学报，2014，30(5)：17-21.

ZHUANG Ya-qiang，ZHANG Chen-xin，ZHANG Xiao-kuan，et al.Statistical Analysis and Simulation of Typical Stealth Aircraft Dynamic RCS[J].Journal of Microwaves，2014，30(5)：17-21.

[10] 陈世春，黄沛霖，姬金祖，等.典型隐身飞机的RCS 起伏统计特性[J].航空学报，2014，35(12)：3304-3314.

CHEN Shi-chun，HUANG Pei-lin，JI Jin-zu.Radar Cross Section Fluctuation Characteristics of Typical Stealth Aircraft[J].Acta Aeronautica et Astronutica Sinica，2014，35(12)：3304-3314.

[11] 黄坦，徐振海，戴崇，等.隐身目标雷达散射截面最优分布模型选择[J].电波科学学报，2014，29(5)：899-904.

HUANG Tan，XU Zhen-hai，DAI Chong，et al.Optimal Distribution Model Selection of Stealth Target RCS[J].Chinese Journal of Radio Science，2014，29(5)：899-904.

[12] 袁礼海，李钊，宋建社.利用高斯混合模型实现概率密度函数逼近[J].无线电通信技术，2007，33(2)：20-22.

YUAN Li-hai，LI Zhao，SONG Jian-she.Probability Density Function Approximation Using Gaussian Mixture Model[J].Radio Communications Technology，2007，33(2)：20-22.

[13] OZGUR E，LEVENT G.Enhancing the Accuracy of the Interpolations and Anterpolations in MLFMA[J].IEEE Transaction on Antennas Propagation，2006，54(12)：3822-3826.

[14] 杨建军，王明宇，张晨新，等.飞机隐身特点与传感器特性剖析[J].空军工程大学学报：军事科学版，2013，13(4)：36-39.

YANG Jian-jun，WANG Ming-yu，ZHANG Chen-xin，et al.Analysis on Stealth Characteristic of Aircraft and Sensor Property[J].Journal of Air Force Engineering University：Military Science ed，2013，13(4)：36-39.

[15] 周品.Matlab概率与数理统计[M].北京：清华大学出版社，2012.

ZHOU Pin.Matlab Probability and Mathematical Statistics[M].Beijing：Tsinghua University Press，2012.

GeneralApproachforStatisticalModelingofRadarTargetRCS

ZHANG Chen-xin1，LIN Cun-kun2，ZHOU Cheng3，ZONG Bin-feng4，DING De-wen5

(1.AFEU,Air and Missile Defense College，Shaanxi Xi’an 710051，China; 2.PLA，No.95972 Troop，Gansu Jiuquan 735018，China；3.The Communication Navigation and Command Automation Institute of the Air Force Equipment Academy，Beijing 100085，China；4.PLA，No.94710 Troop，Jiangsu Wuxi 214000，China; 5.PLA，No.94259 Troop，Shandong Penglai 265600，China)

For the problem that conventional RCS(radar cross section) fluctuation models are built from RCS on centimeter wave frequency band, a general statistical modeling approach based on Gaussian mixture distribution is proposed. Statistical analysis on simulated data and measured data is investigated. The results of goodness-of-fit indicate that the Gaussian mixture distribution can acquire a better performance both on metrewave band and centimeter wave band. The fitting parameters can be estimated directly by curve fitting tools in Matlab. The research results may be used to develop radar detection theory and provide theoretic support for radar design.

radar target；radar cross section(RCS)；RCS fluctuation model；statistical modeling；Gaussian mixture distribution；goodness-of-fit test

2016-11-19；

2017-02-14

张晨新(1969-)，男，安徽宿州人。教授，博士，主要从事雷达目标特性建模研究。

通信地址：710051 陕西省西安市长乐东路甲字1号空军工程大学防空反导学院微波应用教研室E-mail：zyq_1990@126.com

10.3969/j.issn.1009-086x.2017.05.018

TN955

A

1009-086X(2017)-05-0114-06