振动激发对激波反射的影响

彭俊， 张子健， 周凯， 胡宗民,*， 姜宗林

1.中国科学院力学研究所 高温气体动力学国家重点实验室， 北京 100190 2.中国科学院大学 工程科学学院， 北京 100049

振动激发对激波反射的影响

彭俊1,2， 张子健1,2， 周凯1,2， 胡宗民1,2,*， 姜宗林1,2

1.中国科学院力学研究所 高温气体动力学国家重点实验室， 北京 100190 2.中国科学院大学 工程科学学院， 北京 100049

定常激波反射分为规则反射和马赫反射，在不同条件下2种反射结构之间会相互转变。高超声速流动中的激波反射问题常面临高温气体效应，随着温度逐渐升高，最先出现的是空气分子振动激发。通过理论分析和定量计算，研究了振动激发对激波反射及其转变规律的影响。首先给出考虑振动激发的空气热力学模型，并分析其与量热完全气体的差异以及对激波关系的影响；接着分析在规则反射和马赫反射中，振动激发对激波反射流场的影响规律；最后讨论振动激发对激波反射转变2个准则点的影响。研究结果表明，振动激发使激波极线的整体轮廓变大，且这种差异在经过一次激波反射之后被明显放大，会对激波反射的流场产生重大影响；对于激波反射的转变，振动激发使转变的2个准则点都变大，且对规则反射向马赫反射转变的脱体准则影响更大。

激波反射； 振动激发； 马赫反射； 转变准则； 高超声速流动

激波广泛存在于自然界和人类科技活动中，是气体动力学最具特色的基本物理现象之一，是能够在流动内部诱导旋涡的重要物理过程，表现出强间断与非线性的气动物理特征。在激波传播过程中，当传播条件发生改变时，包括壁面出现、流动介质属性改变、其他流场结构存在等，激波会与其产生相互作用而发生反射，形成激波反射流场结构。在不同条件下，会形成各种具有不同特征的激波反射结构，包括规则反射、马赫反射等，出现反射激波、马赫杆、滑移线、三波点等典型流场结构[1]。在某些条件下，甚至会形成双马赫反射、弱激波反射以及一些过渡或反转激波反射结构，出现双马赫杆、前向射流[2-3]、多超声速区[4-5]、拐点[1,6]等特殊流场结构。当产生激波反射的条件发生变化时，各种不同反射结构之间会发生相互转变，存在各种转变准则[1,7-8]。自von Neumann[9-10]于20世纪40年代对激波反射现象进行深入研究开始，经过70多年的努力，人们提出了各种分析理论、试验技术和计算方法，发现了各种激波反射结构，得到了各种波系结构产生的不同物理机制，对激波反射现象的认识越来越深入并日臻完善。

激波反射问题得到广泛深入的研究，除了由于其本身具有的重要流动物理意义之外，更重要的是由于其具有很强的工程应用背景，且在不同应用背景之下，激波反射现象具有不同的利弊。在超/高超声速飞行器机身外表面、翼面以及进气道内，激波在壁面上的反射，会与壁面附近的边界层发生相互作用，在激波反射点附近区域，流动现象很复杂，可能会发生流动分离、激波非定常运动、旋涡运动、压力波动、混合和湍流等问题[11-12]。一旦出现流动分离，产生了分离泡，激波波系会发生变化，进而引起压力载荷的变化，在流动再附点还会引起热流的增加。在超燃冲压发动机进气道和隔离段中，超声速气流进入进气道后形成的定常激波在上下壁面间不断反射，形成一系列激波串，完成来流压缩过程[13-14]。在发动机尾喷管的超声速射流中，斜激波在对称轴反射形成马赫盘以及一系列激波/膨胀波相关的多级反射的菱形结构，对发动机性能产生重要影响[13-15]。在预混可燃气体中的激波反射能形成局部高温高压区，可实现爆轰直接点火或爆燃向爆轰转变，是爆轰现象研究和爆轰发动机研制的关键技术[16-19]。工程上利用与控制激波反射，非常依赖于能否清晰地认识各种反射结构的特征及其产生机理，以及在产生条件发生改变时，各种激波反射结构之间的转变准则。

自21世纪以来，随着高超声速飞行器的深入研究，激波反射的研究范围逐渐拓宽到高超声速领域。高超声速气流通过激波甚至多道激波压缩，空气巨大的动能转变为内能，激波波后温度急剧升高。空气在如此高的温度下将会发生分子振动激发、解离和电离等热化学反应，表现出不同于量热完全气体的特性，使流动规律发生变化，这就是高温气体效应[20-21]。在高温气体效应影响下，激波反射会具有与量热完全气体流动不同的现象和特性，出现与量热完全气体理论预测不一样的激波反射结构和特征，同时各种反射之间的转变准则也会发生变化[22]。Tarnavskii[23]采用等效比热比方法研究了考虑大气真实物理特性时在高超声速飞行器发动机进气道内气流偏转角对不同激波反射结构形成的影响，以及计算了在反射结构中不同区域内的气流参数。高云亮等[24]通过化学反应流的数值模拟研究发现，强激波诱导的高温气体效应使马赫反射的三波点轨迹角变小、马赫杆高度变低、楔顶附体激波倾角变小，并进一步加剧了马赫杆的向前突出。李季[25]建立了化学非平衡流激波关系的理论计算方法，得到了考虑化学非平衡效应的激波极线图，并结合数值模拟研究了化学非平衡对定常激波规则反射和马赫反射迟滞效应的影响。因此，研究考虑高温气体效应下的激波反射问题，对进一步发展激波反射理论、认识新的激波反射物理规律和解决更为复杂的工程实际问题具有重要意义。

空气所处的温度区间不同，高温气体效应中占主导的热化学反应过程也不同，如表1(表中p为压力，且1 atm=1.01×105Pa)所示[11]，随着温度逐渐升高，最先出现的是空气分子振动激发；且在较大的温度范围内(800～2 500 K)，主要的热化学反应过程是分子振动激发，而分子解离、电离等化学反应过程基本没发生，此时可以只考虑振动激发对流动的影响。因此，研究振动激发对激波反射的影响是研究高温气体效应对激波反射影响的第1步。

在各种复杂激波反射结构中，定常激波反射是比较简单和典型的类型。如图1所示，定常激波反射分为规则反射和马赫反射，图中θ为入射气流偏转角，β为激波角，Ma1、Ma2和Ma3分别为来流、入射波后和反射波后的马赫数，Ma4为马赫杆后的马赫数。定常激波反射最早由Mach[26]通过试验研究首次发现，并由von Neumann[9-10]进行了深入研究。其中规则反射结构由2道激波组成：入射激波和反射激波。而马赫反射结构由3道激波(入射激波、反射激波以及马赫杆)和1条滑移线组成，这4个间断面相交于1个三波点。因此，以定常激波反射的2种反射结构为研究对象，对初步认识激波反射现象中的高温气体效应具有重要作用。

本文主要以定常激波反射的2种反射结构，即规则反射和马赫反射为研究对象，研究振动激发对激波反射流场特性和激波反射转变准则的影响。首先给出振动激发下空气的热力学模型，然后利用激波极线讨论振动激发对激波关系和激波反射流场特性的影响，最后讨论振动激发对激波反射转变准则的影响。

表1不同温度区间空气所发生的热化学反应(p=1atm)[11]

Table1Temperaturerangesofthermochemicalreactionprocessforair(p=1atm)[11]

Temperaturerange/KThermochemicalreactionprocess<800Caloricallyperfectgas800-2500Vibrationexcitation2500-4000O2beginstodissociate4000-9000N2beginstodissociate;O2almostcompletelydissociated>9000N2almostcompletelydissociated;ionizationbegins

图1 定常激波反射Fig.1 Steady shock reflections

1 振动激发下的空气热力学模型

假设空气是由79%的N2和21%的O2组成的，即

(1)

各组分的相对分子质量为

MN2=28,MO2=32

(2)

则各组分气体的质量分数分别为

(3)

(4)

各组分气体的气体常数分别为

(5)

(6)

式中：R0=8.314 J/mol为普适气体常数。空气的气体常数为

R=mN2RN2+mO2RO2=288.3 J/(kg·K)

(7)

常温下，空气一般按量热完全气体来处理，其比焓h、定压比热cp和比热比γ等热力学参数满足的关系为

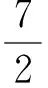
(8)

(9)

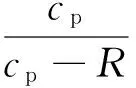
(10)

式中：T为温度。

考虑振动激发后，空气已不再是量热完全气体，比焓h中将会多出振动能项ev，即

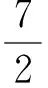
(11)

(12)

式中：Tve，N2和Tve，O2分别为N2和O2的振动特征温度，取值为Tve,N2=3 340 K,Tve,O2=2 230 K[27]。此时，定压比热和比热比则分别为

(13)

(14)

根据量热完全气体的热力学公式(式(8)～式(10))以及考虑振动激发的热力学公式(式(11)～式(14))，2种空气模型的差异随温度的变化如图2所示。可见，由于分子振动能激发，2种模型的差异主要体现在能量上，以及与能量相关的气体属性，如比热、比热比等，进而产生流动上的差异。当温度在300 K以下时，2种模型几乎一模一样，并没有表现出任何可观的差异。随着温度的上升，空气分子的振动自由度开始激发，2种模型的差异逐渐变得明显。当温度上升到800 K时，2种空气模型比焓的差异δh/h为2.50%，定压比热的差异δcp/cp为8.67%，考虑振动激发的比热比从量热完全气体的1.4降低到1.353，此时振动激发对空气热力学性质的影响已不可忽略[22]。当温度达到2 500 K时，2种空气模型比焓的差异为12.64%，定压比热的差异为25.11%，考虑振动激发的比热比从量热完全气体的1.4降低到1.296，此时空气分子振动自由度几乎完全激发，将极大地影响空气的热力学性质及以空气为介质的流动。

对于在温度范围为800～2 500 K内只考虑振动激发而不考虑化学反应所带来的误差，可以通过比较正激波波后参数在量热完全气体、振动激发和热化学反应(振动激发+化学反应)这3种空气模型下的差异得到。设定来流温度T1=226 K、压力p1=0.1 atm、马赫数Ma1=7，此时量热完全气体正激波波后温度T2=2 366 K，接近所给温度范围的上限。振动激发的计算方法将在2.1节中介绍，热化学反应的计算则采用Gaseq小程序，3种空气模型的计算结果如表2所示，表中p2与Ma2分别为正激波后的压力与马赫数，括号内的百分比代表振动激发或热化学反应的结果与量热完全气体相应结果的差异。从表中数据可见，即使温度已经比较接近所给温度范围的上限，振动激发的影响仍起主导作用，化学反应的影响较小。这说明，在2 500 K以下，只考虑振动激发对流动的影响是合理的。

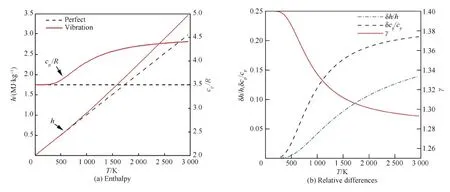
图2 2种空气模型的对比Fig.2 Comparison of two gas models

表2 量热完全气体、振动激发和化学反应3种空气模型下正激波波后参数对比(Ma1=7)

Table2Comparisonofparametersbehindnormalshockforthreegasmodelsofcaloricallyperfectgas,vibrationexcitationandthermochemicalreaction(Ma1=7)

GasmodelT2/Kp2/atmMa2Caloricallyperfectgas23665.700.397Vibrationexcitation2114(-10.7%)5.89(3.3%)0.379(-4.5%)Thermochemicalreaction2090(-11.7%)5.91(3.7%)0.375(-5.5%)

2 振动激发下的激波关系

在激波反射问题中，无论是入射激波、反射激波或者是马赫杆都要用到激波关系。因此，在研究振动激发对激波反射的影响之前，先来研究振动激发对激波关系的影响。在von Neumann提出的分析定常激波反射问题的双激波理论和三激波理论中[10]，限制激波反射求解的边界条件是气流偏转角和静压，因此Kawamura和Saito[28]提出用气流偏转角和静压组成的关系曲线——激波极线来表示和分析激波反射过程。同时，激波极线也是全面表示激波关系的一个有力手段。

2.1 理论计算方法与验证

激波极线可以通过斜激波关系得到。即已知一个气流偏转角θ，通过斜激波关系得到激波极线上的一个点。但注意到，由于最大气流偏转角θm未知，θ的取值范围需要进一步确定，给该方法带来一定困难。然而，激波角β的取值范围一直都是0°～90°。因此，另一个可行的途径是已知一个激波角β，通过正激波关系得到斜激波解和气流偏转角θ，从而对应激波极线上的一个点。量热完全气体的激波关系存在解析解，因此很容易得到量热完全气体的激波极线图。然而，考虑振动激发时，空气的比焓是温度的非线性函数，如式(11)～式(12)，正激波关系没有解析表达式。此时，可从基本方程出发推导得到适用于计算机求解的牛顿迭代公式，其表达式为

(15)

(16)

(17)

(18)

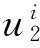
为对该理论计算方法进行验证，在考虑振动激发的激波极线上取气流偏转角θ分别为20°、30° 和40°，将所得理论解与数值模拟的结果进行对比，如表3所示。来流温度T1=226 K，马赫数Ma1=10。数值模拟求解的是考虑振动激发的二维Euler方程，空间上采用AUSMPW+格式[29-30]离散，时间上采用LUSGS隐式格式[31]推进，并采用MUSCL格式[32]对原始变量进行重构。

从表3中各个气流偏转角θ下跨斜激波温度比T21、压力比p21和波后马赫数Ma2等参数的理论解和数值模拟结果的对比发现，两者是非常一致的，说明以上提出的激波极线的理论计算方法是正确的。图3为考虑振动激发时30° 斜劈的压力云图。从图中清晰可见一道斜激波，通过与图上根据激波角的理论值37.36° 画出的一条直线对比发现，两者是平行的，即理论激波角与数值模拟得到的结果也是一致的。

表3考虑振动激发时斜激波关系的理论解和CFD结果对比(T1=226K,Ma1=10)

Table3ComparisonoftheoreticalandCFDsolutionsforobliqueshockrelationwithvibrationexcitation(T1=226K,Ma1=10)

MethodT21p21Ma2θ=20°θ=30°θ=40°θ=20°θ=30°θ=40°θ=20°θ=30°θ=40°Theory4.367.4111.0721.6943.8271.804.443.052.02CFD4.367.4111.0721.6943.8271.804.443.052.02

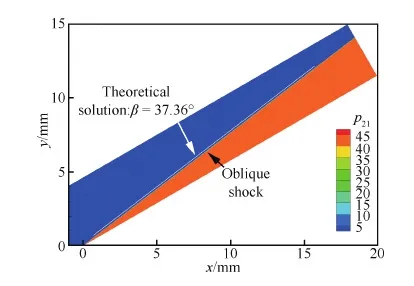
图3 T1=226 K, Ma1=10时30° 斜劈的压力云图(CFD)Fig.3 Pressure contours of a 30° wedge at T1=226 K, Ma1=10 (CFD)

2.2 对比分析

图4为量热完全气体和考虑振动激发的激波极线，激波前温度T1=226 K，马赫数Ma1=10。从图4可见，激波波前状态相同时，同一个气流偏转角对应2个静压比和激波角，即出现2个激波解，其中静圧比和激波角大的为强激波解，另一个为弱激波解。对比量热完全气体的结果，考虑振动激发后激波极线的整体轮廓变大了。对于强激波解，考虑振动激发的波后压力明显变大，激波角也变大。而对于弱激波解，考虑振动激发的波后压力变小，激波角也变小。在激波极线中，最明显的特征就是最大气流偏转角，它是斜激波与脱体激波的临界角，与规则反射向马赫反射的转变密切相关。图4的结果表明，考虑振动激发后最大气流偏转角与量热完全气体的相比明显增大。后面的讨论指出，这将对规则反射和马赫反射之间的转变产生重要影响。

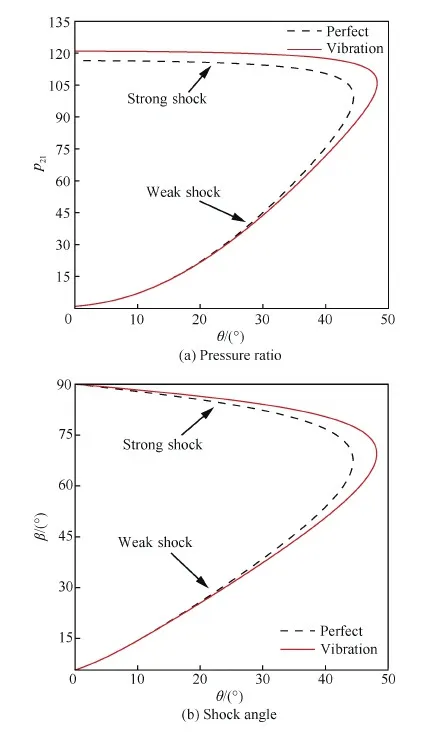
图4 激波极线对比Fig.4 Comparison of shock polars

考虑振动激发后，强激波解与弱激波解的波后压力变化方向不同。而强激波解所对应的波后流动一般为亚声速，弱激波解的波后一般为超声速流动。这说明，振动激发对强激波和弱激波后的高超声速飞行器的气动力将会产生不同方向的影响，尤其对周围存在跨声速流动的飞行器如航天飞机等的俯仰力矩影响更大。如图5所示，当钝头体以大攻角飞行时，背风面压力受振动激发的影响较迎风面的小得多。迎风面上，在头部产生弓形激波，波后存在一个声速面。声速面前是亚声速流动，对应强激波解，振动激发使波后压力变大；而声速面后是超声速流动，对应弱激波解，振动激发使波后压力变小，这就产生一个由振动激发导致的附加俯仰力矩。

取气流偏转角θ=30°，求出强激波解和弱激波解所对应的跨激波压力比、温度比、密度比(ρ21)、速度比(u21)等参数，如表4所示。可见，振动激发对激波后温度、密度和马赫数的影响较大，超过10%。其中，振动激发对强激波波后密度的影响超过20%，由于激波前后密度比与激波脱体距离直接相关，这说明振动激发对强激波的激波脱体距离也会产生重大影响。而振动激发对波后压力和激波角的影响较小，在5%以内。对于激波后的速度，振动激发对弱激波的影响较小，而对强激波的影响很大，达19.63%。另外，除激波后的温度和密度之外，振动激发对激波后的压力、速度、马赫数和激波角的影响，在强激波和弱激波中影响方向是相反的，具有不同的变化趋势。

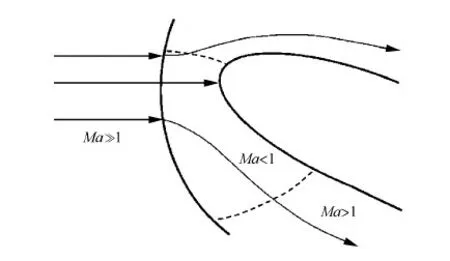
图5 大攻角飞行钝头体流场Fig.5 Flow field of blunt body with large angle of attack

表4 T1=226 K, Ma1=10时的斜激波关系Table 4 Oblique shock relations at T1=226 K, Ma1=10

Gasmodelp21T21ρ21β/(°)u21Ma2WeakshockwavePerfect45.098.485.3138.520.7912.72Vibration43.847.415.9137.360.8013.05Difference/%-2.77-12.6111.30-3.011.3012.13StrongshockwavePerfect114.3920.045.7182.290.2190.49Vibration119.6017.176.9784.060.1760.44Difference/%4.55-14.3222.062.15-19.63-10.20

3 振动激发下的激波反射

定常激波反射分为规则反射(RR)和马赫反射(MR)，可以借助激波极线进行分析，如图6所示，图中θa、θb、θc、θⅠ、θⅡ为与极线a、b、c、Ⅰ、Ⅱ对应的气流偏转角。当反射激波极线位于极线Ⅰ右侧时，即θ>θⅠ时，可以形成马赫反射，比如极线c。极线Ⅰ与纵轴以及入射激波极线共同交于一点，对应马赫反射向规则反射转变的von Neumann准则。当反射激波极线位于极线Ⅱ的左侧时，即θ<θⅡ时，可以形成规则反射，比如极线a。极线Ⅱ与纵轴相切，对应规则反射向马赫反射转变的脱体准则。当反射激波极线位于极线Ⅰ与极线Ⅱ之间时，即θⅠ<θ<θⅡ时，规则反射和马赫反射都可能形成，即出现双解区。

图6 规则反射和马赫反射的激波极线 Fig.6 Shock polars of regular reflection and Mach reflection

3.1 规则反射

当气流偏转角θ小于脱体准则点θⅡ时，可以形成如图1(a)所示的规则反射，此时反射激波极线与纵轴有2个交点，即反射激波也存在强解与弱解。在实际中一般都是出现弱激波解，即激波反射的解一般取压力激波极线中与纵轴相交压力较小的点，在速度激波极线中则是取速度较大的点。图7为量热完全气体与考虑振动激发的压力激波极线和速度激波极线。表5为反射激波后流场参数的对比，表中p31、T31、ρ31、u31分别对应图7 中③区和①区气流的压力比、温度比、密度比和速度比，β2-3为反射激波与②区气流的夹角。来流温度T1=226 K，马赫数Ma1=10，气流偏转角θ=30°。

从图7可见，无论是入射激波还是反射激波，考虑振动激发后，激波极线与量热完全气体的相比其整体轮廓都变大了。从反射激波极线的差异可见，振动激发带来的激波极线的差异经过一次激波反射后被放大了。即经过一次激波反射，振动激发对波后流场的影响变得更大。结合表4和表5可得，振动激发对激波后压力的影响，从入射激波的-2.77%被放大到反射激波的-2.92%，影响大小及其变化对压力而言不是很明显。然而对于激波后的速度，振动激发的影响从入射激波的1.30%被放大到反射激波的9.00%，变化及影响大小都非常明显。另外还可算出反射激波后的温度、密度、马赫数和反射激波角，以及振动激发的影响大小。结果表明，从入射激波到反射激波，振动激发对激波后的温度、密度、马赫数和激波角等流场参数的影响都被明显放大。

图7 规则反射的激波极线分析Fig.7 Shock polar analysis of regular reflection

表5 T1=226 K, Ma1=10, θ=30° 时规则反射的激波关系Table 5 Shock relations of regular reflection at T1=226 K, Ma1=10, θ=30°

Gasmodelp31T31ρ31β2-3/(°)u31Ma3Perfect261.3316.2116.1256.340.4891.22Vibration253.7012.7019.9748.500.5331.63Difference/%-2.92-21.6523.88-13.929.0033.61

3.2 马赫反射

当气流偏转角θ大于von Neumann准则点θⅠ时，可以形成如图1(b)所示的马赫反射。此时在压力激波极线图上，反射激波极线与入射激波极线的强解部分相交，交点对应的转角和压力就是马赫杆后在三波点附近以及反射激波后的气流偏转角和压力。而在速度激波极线图上，相应的气流偏转角对应反射激波极线上的2个点，其中速度较大的点3对应反射激波后的状态，速度较小的点4对应马赫杆后在三波点附近的状态。图8 为量热完全气体与考虑振动激发的压力激波极线和速度激波极线，表6为反射激波后滑移线两侧流场参数的对比，表中θ3为反射激波的气流偏转角；p31、u31、ρ31、T31对应图8中③区与①区的压力比、速度比、密度比和温度比，u41、ρ41、T41的含义与之类似；Δu34,1为u41和u31的差值，Δρ34,1和ΔT34,1的含义与之类似。来流温度T1=226 K，马赫数Ma1=10，气流偏转角θ=40°。

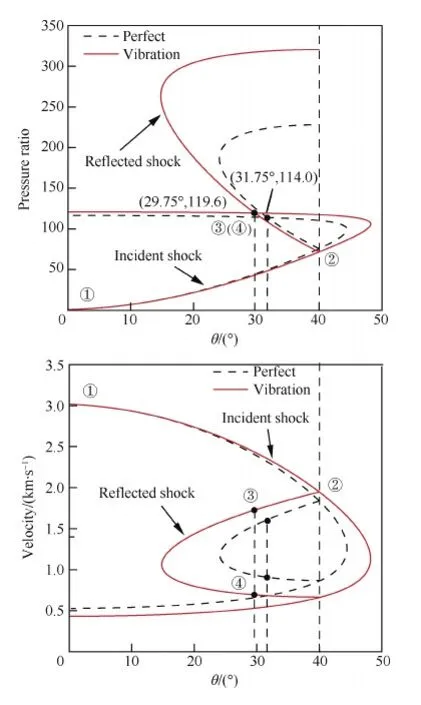
图8 马赫反射的激波极线分析Fig.8 Shock polar analysis of Mach reflection

可见，与规则反射一样，从入射激波到反射激波，振动激发对流场参数的影响被明显放大。然而马赫杆是单激波，振动激发对马赫杆后流场参数的影响并没有被放大。由此，振动激发会对滑移线两侧流场参数的差异产生较大影响。从表6可见，振动激发对滑移线两侧速度差异的影响为11.76%，而对滑移线两侧密度差异的影响达51.81%。滑移线两侧的速度差异与KH(Kelvin-Helmholtz)不稳定性直接相关，考虑振动激发后滑移线两侧的速度差异变得更大，这说明振动激发对流动稳定性也会产生一定影响。另外，振动激发对三波点后的气流偏转角产生了24.24%的影响。而对三波点后压力的影响，与规则反射不同，考虑振动激发后压力变大，影响大小为4.93%。

表6 T1=226 K, Ma1=10, θ=40°时马赫反射的激波关系Table 6 Shock relations of Mach reflection at T1=226 K, Ma1=10, θ=40°

4 振动激发对激波反射转变的影响

如前所述，可以通过控制气流偏转角θ来实现定常激波反射在2种反射结构之间转变，且这种转变存在迟滞现象。即理论上仅当气流偏转角θ大于脱体准则点θⅡ时，规则反射才向马赫反射转变；仅当气流偏转角θ小于von Neumann准则点θⅠ时，马赫反射才向规则反射转变，迟滞区为θⅠ<θ<θⅡ。

图4中指出，考虑振动激发后最大气流偏转角与量热完全气体的相比明显增大。而从图7和图8可见，振动激发引起的最大气流偏转角的差异在经过一次激波反射后被明显放大，这将对规则反射向马赫反射转变的脱体准则点的预测产生重大影响。图9为激波反射转变的2个准则点以及对应的激波角和气流偏转角随来流马赫数的变化。表7为2个激波反射转变准则点在2种气体模型下的具体差异。来流温度T1=226 K,马赫数Ma1=10。

可见，激波反射转变的迟滞现象在马赫数Ma1≈2.2时开始出现，且随着马赫数的增大，迟滞区逐渐变宽。考虑振动激发后，激波反射转变的2个准则点θⅠ、θⅡ都相应地变大。且脱体准则点变大较明显，而von Neumann准则点变化较小，这导致激波反射转变的迟滞区明显变宽。从表7的数据来看，在马赫数Ma1=10时，考虑振动激发后von Neumann准则点θⅠ的差异在0.5°以内，影响大小为2.20%；而对于脱体准则点θⅡ，振动激发的影响较大，角度差异约为3°，影响大小为9.59%。脱体准则点θⅡ约3°的差异，对于认识存在振动激发的高超声速流动中的激波反射转变现象，以及在试验中观察和在工程中控制马赫反射具有重大意义。

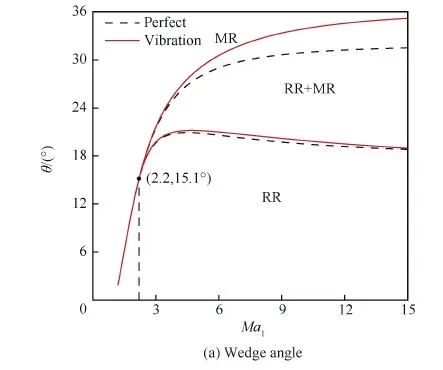
图9 规则反射和马赫反射之间的转变准则Fig.9 Transition criterion between regular reflection and Mach reflection

表7T1=226K,Ma1=10时规则反射和马赫反射之间的临界转变角

Table7CriticaltransitionanglesbetweenregularreflectionandMachreflectionatT1=226K,Ma1=10

GasmodelθⅠ/(°)θⅡ/(°)Perfect19.5230.91Vibration19.9533.87Difference/%2.209.59

5 结 论

1) 研究结果表明，振动激发使激波极线的整体轮廓变大，对强激波和弱激波具有不同的影响规律。振动激发使强激波波后压力变大，而使弱激波波后压力变小。振动激发对激波流场的影响在经过一次激波反射之后被明显放大，分别对规则反射和马赫反射的流场参数产生重大影响。

2) 对于激波反射类型的转变，振动激发使转变的2个准则点都变大，迟滞区变宽，且对规则反射向马赫反射转变的脱体准则影响更大。对认识存在振动激发的高超声速流动中的激波反射转变现象，以及在试验中观察和在工程中控制马赫反射具有重大意义。

[1] BEN-DOR G. Shock wave reflection phenomena[M]. 2nd ed. Berlin: Springer-Verlag Press, 2007.

[2] LI H, BEN-DOR G. Analysis of double-Mach-reflection wave configuration with convexly curved Mach stems[J]. Shock Waves, 1999, 9(5): 319-326.

[3] VASILEY E I, BEN-DOR G, ELPERIN T, et al. The wall-jetting effect in Mach reflection: Navier Stokes simulations[J]. Journal of Fluid Mechanics, 2004, 511: 363-379.

[4] TESDALL A M, HUNTER J K. Self-similar solutions for weak shock reflection[J]. SIAM Journal on Applied Mathematics, 2002, 63(1): 42-61.

[5] SKEWS B W, LI G, PATON R. Experiments on Guderley Mach reflection[J]. Shock Waves, 2009, 19(2): 95-102.

[6] MORIOKA T, SUZUKI Y, HONMA H. Radiation observation of strong shock wave reflection in air[C]//22th International Symposium on Shock Waves. London: Imperial College, 2000: 1201-1206.

[7] BEN-DOR G. A state-of-the-knowledge review on pseudo-steady shock-wave reflections and their transition criteria[J]. Shock Waves, 2006, 15(3): 277-294.

[8] VASILEY E I, ELPERIN T, BEN-DOR G. Analytical reconsideration of the von Neumann paradox in the reflection of a shock wave over a wedge[J]. Physics of Fluids, 2008, 20(4): 819-299.

[9] VON NEUMANN J. Oblique reflection of shocks: Explosion research report 12[R]. Washington, D.C.: Navy Department, 1943.

[10] VON NEUMANN J. Refraction, intersection and reflection of shock waves: NAVORD Report 203-45[R]. Washington, D.C.: Navy Department, 1943.

[11] ANDERSON J D. Hypersonic and high-temperature gas dynamics[M]. 2nd ed. Reston, VA: AIAA, 2006: 385-386.

[12] KIM H D, SETOGUCHI T. Shock induced boundary layer separation[C]//8th International Symposium on Experimental and Computational Aerothermodynamics of Internal Flows, 2007.

[13] HEISER W, PRATT D, DALEY D, et al. Hypersonic airbreathing propulsion[M]. Reston, VA: AIAA, 1994.

[14] GOONKO Y P, LATYPOV A F, MAZHUL I I, et al. Structure of flow over a hypersonic inlet with side compression wedges[J]. AIAA Journal, 2015, 41(3): 436-447.

[15] KLEINE H, SETTLES G S. The art of shock waves and their flowfields[J]. Shock Waves, 2008, 17(5): 291-307.

[16] JIANG Z L, TAKAYAMA K. Reflection and focusing of toroidal shock waves from coaxial annular shock tubes[J]. Computers and Fluids, 2013, 27(5-6): 553-562.

[17] JACKSON S, GRUNTHANER M, SHEPHERD J. Wave implosion as an initiation mechanism for pulse detonation engines: AIAA-2003-4820[R]. Reston, VA: AIAA, 2003.

[18] IZUMI K, ASO S, NISHIDA M. Experimental and computational studies focusing process of shock waves reflected from parabolic reflectors[J]. Shock Waves, 1994, 3(3): 213-222.

[19] 滕宏辉， 张德良， 李辉煌， 等. 用环形激波聚焦实现爆轰波直接起爆的数值模拟[J]. 爆炸与冲击， 2005, 25(6): 512-518.

TENG H H, ZHANG D L, LI H H, et al. Numerical investigation of detonation direct initiation induced by toroidal shock wave focusing[J]. Explosion and Shock Waves, 2005, 25(6): 512-518 (in Chinese).

[20] 姜宗林. 触摸高温气体动力学[J]. 力学与实践， 2006, 28(5): 1-7.

JIANG Z L. Feeling high temperature gas dynamics[J]. Mechanics in Engineering, 2006, 28(5): 1-7 (in Chinese).

[21] 樊菁. 高超声速高温气体效应判据[J]. 力学学报， 2010, 42(4): 591-596.

FAN J. Criteria on high-temperature gas effects around hypersonic vehicles[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(4): 591-596 (in Chinese).

[22] 杨旸， 姜宗林， 胡宗民. 激波反射现象的研究进展[J]. 力学进展， 2012, 42(2): 141-161.

YANG Y, JIANG Z L, HU Z M. Advances in shock wave reflection phenomena[J]. Advances in Mechanics, 2012, 42(2): 141-161 (in Chinese).

[23] TARNAVSKII G A. Influence of flow angularities in a hypersonic ramjet diffuser of the formation of the shock-wave structure of the real gas flow[J]. Journal of Engineering Physics and Thermophysics, 2004, 77(3): 651-662.

[24] 高云亮， 李进平， 胡宗民， 等. 准定常强激波马赫反射波形的数值模拟[J]. 空气动力学学报， 2008, 26(4): 456-461.

GAO Y L, LI J P, HU Z M, et al. A numerical investigation on the Mach reflection patterns of quasi-steady strong shock waves[J]. Acta Aerodynamica Sinica, 2008, 26(4): 456-461 (in Chinese).

[25] 李季. 高温非平衡效应下的激波干扰与激波反射[D]. 合肥： 中国科学技术大学， 2015.

LI J. On shock interactions and reflections with high temperature non-equilibrium effects[D]. Hefei: University of Science and Technology of China, 2015 (in Chinese).

[26] MACH E. Uber den verlauf von funkenwellen in der ebene und im raume[J]. Sitzugsbr Akad Wiss Wien, 1878, 78: 819-838.

[27] 汪志诚. 热力学·统计物理[M]. 第四版. 北京： 高等教育出版社， 2008: 208.

WANG Z C. Thermodynamics and statistical physics[M]. 4th ed. Beijing: Higher Education Press, 2008: 208 (in Chinese).

[28] KAWAMURA R, SAITO H. Reflection of shock waves-1: Pseudo-stationary case[J]. Journal of Physical Society Japan, 1956, 11(5): 584-592.

[29] KIM K H, KIM C, RHO O H. Methods for the accurate computations of hypersonic flows: I. AUSMPW+ scheme[J]. Journal of Computational Physics, 2001, 174(1): 81-119.

[30] KIM K H, LEE J H, RHO O H. An improvement of AUSM schemes by introducing the pressure-based weight functions[J]. Computers & Fluids, 1998, 27(3): 311-346.

[31] YOON S, JAMESON A. Lower-upper Symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations[J]. AIAA Journal, 2012, 26(9):1025-1026.

[32] LEER B V. Towards the ultimate conservative difference scheme: V. A second-order sequel to Godunov’s method[J]. Journal of Computational Physics, 1979, 32(1): 101-136.

(责任编辑： 王娇)

*Correspondingauthor.E-mail:huzm@imech.ac.cn

Effectsofvibrationexcitationonshockreflections

PENGJun1,2,ZHANGZijian1,2,ZHOUKai1,2,HUZongmin1,2,*,JIANGZonglin1,2

1.StateKeyLaboratoryofHigh-temperatureGasDynamics,InstituteofMechanics,ChineseAcademyofSciences,Beijing100190,China2.SchoolofEngineeringScience,UniversityofChineseAcademyofSciences,Beijing100049,China

SteadyshockreflectionsincluderegularreflectionandMachreflection,whichcantransittoeachotherundercriticalconditions.High-temperaturegaseffectisinevitableinhypersonicshockreflections.Astemperatureincreases,thevibrationexcitationofairmoleculescomesfirst.TheoreticalanalysisandquantitativecalculationareconductedtostudytheeffectsofvibrationexcitationonshockreflectionsandthetransitionsbetweenregularreflectionandMachrefection.Athermodynamicmodelforairwithvibrationexcitationispresentedandthencomparedwiththecaloricallyperfectgasmodel.Theinfluencesofvibrationexcitationonshockrelations,ontheflowfieldsinregularreflectionandMachreflection,andonthetransitioncriteriabetweenthemareanalyzed.Theresultsshowthatvibrationexcitationmayenlargetheoverallprofileoftheshockpolarascomparedwiththeshockpolarinthecaloricallyperfectgas.Inaddition,thedifferenceintheoverallpolarprofilesisamplifiedsignificantlyforthereflectedshock,andmayalterthereflectionconfiguration.Regardingtheshockreflectiontransitioncriteria,vibrationexcitationmaycauseincreasesofbothtransitionangles,i.e.,thedetachmentcriterionandvonNeumanncriterion,andtheincrementoftheformerismuchlargerthanthelatter.

shockreflection;vibrationexcitation;Machreflection;transitioncriterion;hypersonicflow

2016-12-15；Revised2017-01-04；Accepted2017-02-24；Publishedonline2017-03-231750

URL：www.cnki.net/kcms/detail/11.1929.V.20170323.1750.008.html

s：NationalNaturalScienceFoundationofChina(11672308,11532014)

2016-12-15；退修日期2017-01-04；录用日期2017-02-24； < class="emphasis_bold">网络出版时间

时间：2017-03-231750

www.cnki.net/kcms/detail/11.1929.V.20170323.1750.008.html

国家自然科学基金 (11672308，11532014)

.E-mailhuzm@imech.ac.cn

彭俊， 张子健， 周凯， 等． 振动激发对激波反射的影响J． 航空学报,2017,38(8):121055.PENGJ,ZHANGZJ,ZHOUK,etal.EffectsofvibrationexcitationonshockreflectionsJ.ActaAeronauticaetAstronauticaSinica,2017,38(8):121055.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121055

V211.22

A

1000-6893(2017)08-121055-11