基于高阶统计量和星座图的通信制式识别研究

可飞龙 卓智海 汪毓铎

（北京信息科技大学信息与通信工程学院，北京100101）

基于高阶统计量和星座图的通信制式识别研究

可飞龙 卓智海 汪毓铎

（北京信息科技大学信息与通信工程学院，北京100101）

针对实际工程中基于高阶累计量的调制方式识别方法对信噪比要求较高且对部分调制方式识别率低的问题，本文提出了基于双谱分析和星座图相结合的一种新的调制方式识别方法。基于高阶累积量提取特征值，进一步对取得的累积量特征值求傅里叶变换得到接收信号的双谱分析，对QPSK、OFDM和QAM调制信号进行分类识别，对于QAM调制中的16QAM、32QAM和64QAM调制方式再依据星座图结果进行识别。通过实验数据表明，此调制方式识别方法识别率较高，高阶谱分析对信噪比要求低。

高阶谱；高阶累计量；调制方式识别；星座图

1 引言

非协作通信是在通信双方正常通信的前提下接入到合作通信系统的通信方式，是一种非授权接入通信模式[1]。非协作通信中接收方不能提前获取发送方的信号调制方式等参数，因此要在非协作通信中识别出信号的调制方式和对应的参数较为复杂。因此本文研究非合作通信中的调制识别的问题。

目前的调制方式识别方法主要有两大类[1]：基于特征值参数的识别方法和基于决策论的假设检验识别方法。基于特征值分类的算法通过提取信号的特征值来进行分类接收信号。常用的特征值参数有瞬时幅度、相位、高阶统计量、频谱特征等。此类方法好处是运算复杂度低，时间成本小，适用于实际工程应用。在文献[2]中已提出相关方法，但对QAM调制方式识别率低。利用神经网络和支持向量机的识别方法也有较高的识别率[3]，但因算法迭代次数高，识别过程中耗时长而不适用于工程应用。基于决策论的识别算法主要通过降低识别错误率来探索一种最优的分类方法。虽然目前已经提出一些理论算法，但是由于决策论识别算法分析难度大，算法复杂度高，在工程中应用较少。本文通过分析基于高阶累积量识别方法的不足，提出了基于高阶谱和星座图相结合的调制方式识别方法。

2 接收信号模型

在一般通信系统中，接收端的信号模型为：

其中，n(t)为加性高斯白噪声，x(t)为已调信号，在考虑多径的情况下，接收端信号可进一步表示为：

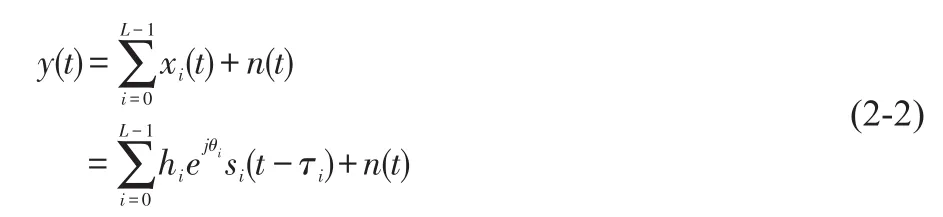
其中hi、τi和θi分别为不同路径的衰减系数，相对延迟和相位因子。s(t)为已调信号，根据不同的调制方式，已调信号的具体表示方式如下：

当调制模式为PSK调制时，已调信号为：

当调制模式为QAM调制时，已调信号为：

当调制模式为OFDM调制时，已调信号为：

上述式中，S为信号功率，u(t)为一个能量有限信号，Cn,k为基带发送的信号，Np为OFDM子载波数。

3 非协作通信中调制方式识别算法

首先计算接收信号的高阶累积量，通过提取基于高阶累积量的特征值对QPSK、16QAM、64QAM和OFDM进行分类。与此同时对计算得到的高阶累积量进行傅里叶变换得到信号高阶谱特征，通过分析高阶谱来分类QPSK和OFDM，最后利用星座图对不同进制的QAM调制方式进行分类识别。对比前后两种方法的识别效果。

3.1 多径信道下求信号的高阶累积量并提取特征值

根据高阶累积量的性质[5]可知，对高斯白噪声求高阶（大于二阶）累计量的结果为零，所以高阶累积量可很好地抑制高斯白噪声。假设一个具有零均值的平稳复随机过程s(k)，它的p+q阶矩可分别表示为[5]：

同样p+q阶累积量可表示为：

由于矩与其累积量的相对变元具有可加性的性质可知，统计独立变量先求和再求累积量等于对其先求累积量再求和。所以依据式（2-1）所描述的接收端信号模型特点，其部分累积量可表示如下：

而发送信号的累积量可表示为：

在识别过程中，通过分析高阶累积量的性质，文献[5]提取的特征值为：

因为接收信号的四阶累积量中高斯噪声为零，所以：

将上式代入式（3-5）得：

最终通过式（3-7）理论计算得出的五种调制方式的特征值为：

表1 Fy取值

对接收信号求取高阶累积量，并按照式（3-7）提取特征值，通过多次试验确定每种调制方式的特征值实际波动范围，依次定义识别门限F1和F2。实际对接收信号求取特征值时，当多次测量结果取平均后，对应的判别结果如下：

表2 特征值判别结果

由于QAM的基于高阶累计量的特征值分辨率较低，所以此方法对其分类效果较差。在低信噪比时，四种调制方式识别率较低。

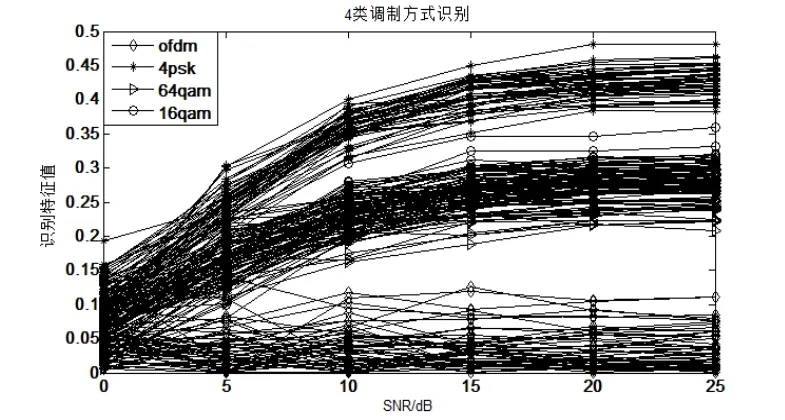
图1 四类调制方式识别结果

基于高阶累计量的特征值分类方法实验仿真结果如图1所示，在信噪比低于5dB时识别率较低，整个过程对于16QAM和64QAM基本无法识别。

3.2 通过高阶谱分析对信号进行分类

针对3.1节中对所述的调制方式识别的不足，本节对此进行了以下改进。在3.1节的基础上，对得到的三阶累积量进行二维傅里叶变换，求其高阶累积量谱。

高阶谱分析相对于功率谱分析来讲可抑制高斯噪声，而且分辨率较高，可以得到信号的幅度和相位等信息，通过将星座图与高阶谱结合起来可有效地对前五类信号进行识别分类。上节介绍了高阶累积量的定义，在上节的基础上可对求得的三阶累积量进行二维傅里叶变换，得到所求信号的双谱。因为此方法运算量相对于较低，识别时间短，故而有利于实际工程应用。

双谱估计可通过直接法和间接法这两种非参数化方法来得到。直接法先将数据分成K段后，对每段数据进行离散傅里叶变换，再对离散傅里叶变换的系数求三重相关，即可得到双谱估计；间接法同样先将数据分成K段后，求各段数据的三阶累积量，然后再对三阶累积量估计值进行二维傅里叶变换。本文在基于文献[5]的基础上，利用间接法对所得到的三阶累积量进行二维傅里叶变换。

利用间接法来进行双谱估计时，首先将长度为N的实验数据s(i)分成K段，每段有M个数据；然后对第j段数据sj(i)计算三阶累积量为：

将K段所有数据的三阶累积量的平均值作为要观测数据的三阶累积量估计，即：

对式（3-9）求二维傅里叶变换得：

上式中L＜M-1，ω(i,l)为二维滞后窗函数，仿真中用Parzen窗做滞后窗函数。

3.3 通过星座图对QAM信号进行分类

对于16QAM、32QAM、64QAM调制，因星座图对称分布，所以部分偶阶矩为零，累积量和双谱估计特征不明显，谱峰位置和幅度信息没有像QPSK调制一样规律，所以本文提出结合星座图的方法对QAM调制信号进行分类。分类前利用数字前端对接收信号进行载频估计和下变频处理，之后估计接收码元速率，对前端采样速率进行调整，同时利用码元定时来对接收数据再进行采样，最终得到码元同步序列。以上处理流程如下：

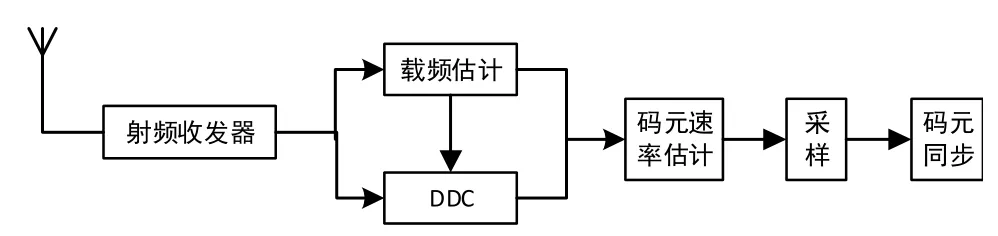
图2 接收信号码元同步预处理

通过射频收发器接收到QAM调制信号，先对其载波粗估计一个频率fc，经过下变频和滤波之后可得到估计载频和实际载频之间的频偏差Δfc，滤波之后得到的信号为：

上式中g(n-mTs)为码元间隔为Ts的脉冲函数，θc为误差相位，基带信号为Rneθm，因为MQAM调制信号星座图的对称性，则在一些对称点上星座图的值不为零，即：

其中k可取任意自然数使得相角θm时不为零，为了取得载波频差，对经过低通滤波器的信号做傅里叶变换，显然在Δfc处会出现峰值，因此可得到载频估计为：fc+Δfc。利用估计到的载波频率可对接收信号进行下变频，然后利用文献[8]提出的基于包络的定时算法实现码元同步序列的获取。利用估计得到的载频f根据公式[9]可得到相偏估计：

由式（3-11）经过傅里叶变换得到的载频估计和式（3-13）得到的相偏估计两个信号参数，利用同步序列和以上两个参数相乘可以消除信号对星座图中散点的影响，从而得到较好的星座图。

4 实验仿真结果

为验证本文提出的识别方法的有效性，利用Matlab2012仿真平台对算法进行仿真。仿真过程考虑多径对接收信号的影响，对QPSK、OFDM、16QAM、32QAM和64QAM五种调制方式的已调信号进行识别，仿真结果如下系列图。

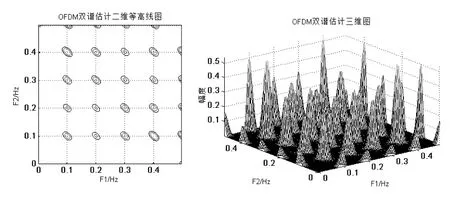
图3 OFDM调制下接收信号双谱估计

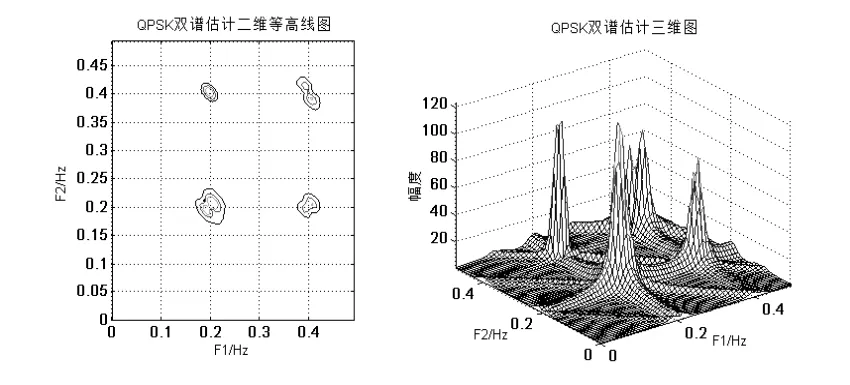
图4 QPSK调制下接收信号双谱估计

图5 M-QAM调制接收信号星座图

四类不同调制方式分类识别结果如图3至图5所示。OFDM模式下，选择6条多径信道，256个子载波，为了便于验证和分析，各子载波均采用QPSK调制；QAM模式下，选用16QAM和64QAM分别对基带发送信号进行调制，随机生成6000个二进制比特流作为基带信号，信号调制后加入加性高斯白噪声；QPSK模式下，对幅度为3的正弦信号取500个采样点做基带发送信号数据，经过调制后加入加性高斯白噪声作为待识别的接收信号。基于双谱特征分析时，由于高斯白噪声的二阶累积量以上均为零，所以经过三阶累积量的傅里叶变换得到的双谱对高斯噪声不敏感，抑制噪声能力较较强，图3和图4为信噪比在5dB时测到的结果，在仿真过程中对信噪比从0dB到20dB变化，但是双谱分析后结果基本相同。所以可以说明基于高阶谱的识别方法相对于文献[3]提出的识别方法在抗噪性能上有较大改善；因QAM调制特性，高阶谱特征不明显，在基于星座图识别时，matlab模拟信号预处理过程，在信噪比为20dB时仿真实现载频和相偏估计，最终对3种进制的QAM调制方式星座图结果较为清晰，相比文献[3]提出的对16QAM和64QAM识别效果不明显（分辨率要求高为0.01），基于星座图的识别方法对三种结果识别较为明显。

5 结束语

调制方式识别以往大多用于军事领域，在非协作通信前提下识别敌方通信制式以获取战略情报。但是随着民用无人机的普及，越来越多的“黑飞”事件发生。本文以防止无人机“黑飞”为出发点，研究无人机常用的通信调制方式，在基于高阶累积量基础上对接收到的信号进一步做傅里叶变换进行特征分析。从仿真结果可以看出，相对于高阶累计量对四类调制方式的识别情况，高阶谱分析结合星座图可以很好地区分QPSK、OFDM、16QAM、32QAM和64QAM的调制。相对于累积量的特征分析，本文提出的制式识别方法相对更适用于实际工程应用。

[1] 许小东．非协作数字通信系统盲解调关键技术研究[D]．合肥：中国科学技术大学，2007．

[2] 詹亚峰．通信信号自动制式识别及参数估计[D]．北京：清华大学，2004．

[3] 张孟伯，张岱，杨晓静．ZP-OFDM信号子载波调制样式的识别[J]．电子信息与对抗技术，2015，30(2)：21-25．

[4] A．E．Sherme，A novel method for automatic modulation recognition，Appl．Soft Compute，2012，12(1)：453-461．

[5] 张贤达．现代信号处理(第2版)[M]．北京：清华大学出版社，2002．

[6] Mahmoud M．Shakra，Ehab M．Shaheen．Automatic Digital Modulation Recognition of Satellite Communication Signals，32ndNational Radio Science Conference．24-26，March 2015．

[7] 孙洁娣，靳世久．基于小波包能量及高阶谱的特征提取方法[J].天津大学学报，20106(6)：562-566．

[8] 廖灿辉，涂世龙，万坚．一种抗频偏的卫星幅相调制信号识别算法[J]．电子与信息学报，2014，36(2)：332-346．

[9] Ciblat P，Ghogho M．Blind NLLS carrier frequency offset estimation for QAM，PSK，and PAM modulation：performance at low SNR[J]．IEEE Transactions on Communications，2006，54(10)：1725-1730．

[10] Ivan A．Hashim，Jafar W．Abdul Sadah，Thamir R．Saeed&Jawad K．Ali(2015)Recognition of QAM Signals with Low SNR Using a Combined ThresholdAlgorithm，IETE Journal of Research，61：1，65-71．

[11] Abdelaziz Bouzegzi，Philippe Ciblat，Pierre Jallon．New algorithms for blind recognition of OFDM based systems．Signal Processing 90(2010)：900-913．

[12] Wu Juan-ping，Han Ying-zheng，Zhang Jin-mei，Wang Hua-kui．Automatic Modulation Recognition of Digital Communication Signals[J]．Communications Technology，2008，334(2)：241-273．

Research on Communication Modulation Recognition Using Higher Order Statistics and Constellation

Ke FeilongZhuo ZhihaiWang Yuduo
(Beijing Information Science&Technology University,Beijing 100101)

In order to decrease the effects involved in SNR and improve the recognition rate when we get the information of modulation in practical engineering.This paper proposes a new method of modulation recognition based on bispectrum analysis and constellation.Based on the eigenvalues extracted from higher order cumulant,the FFT of the cumulative value is obtained by bispectrum analysis of the

signal and then QPSK,OFDM and QAM modulation signals are classified and identified.Then 16QAM,32QAM and 64QAM modulations are identified based on the results of constellation.The experimental data shows that the result of recognition method is better than the other way based on higher order cumulant.

higher order spectrum;high order cumulant;modulation recognition;constellation

TN91

A

1008-6609(2017)09-0001-04

可飞龙（1992-），男，山西忻州人，硕士，研究方向为非协作通信下调制方式识别研究。

北京市教委科研计划项目，项目编号：KM201711232009。