迈克耳孙-莫雷实验的预期与实际模拟

潘尹凡 瞿 霞 冯 杰 郭长江

(上海师范大学数理学院 上海 200234)

迈克耳孙-莫雷实验的预期与实际模拟

潘尹凡 瞿 霞 冯 杰 郭长江*

(上海师范大学数理学院 上海 200234)

通过对迈克耳孙-莫雷实验的预期与实际计算机模拟对比，凸显经典时空观的问题.同时补充了普遍仅对中心位置分析计算的遗憾，给出了完整的模拟图样，以帮助理解该实验的思想原理.

迈克耳孙-莫雷实验 预期模拟 Matlab GUI

1900年4月27日，开尔文男爵在他的演讲中道出了物理学历史中经久不衰的比喻——19世纪笼罩在热和光动力理论上空的乌云.那两朵乌云如同是日后物理学书籍中必不可少的一种定式化修辞，一次次重现着狂风暴雨前夜物理学界自满又不安的空气[1].其中的一朵乌云是1887年由迈克耳孙与莫雷教授重做的“以太漂移”实验，即著名的迈克耳孙-莫雷实验，该实验动摇了绝对静止参考系的时空观，对日后相对论的产生有着不可忽视的作用.

1 对条纹变化分析的不足

目前部分物理书籍在论述迈克耳孙-莫雷实验时，为得出0.37个条纹移动的预期结果，多采用如下方式得出结论.

如图1(a)所示,光经分光板后，透射光先“追光”，后经反射“迎光”，整个过程耗时

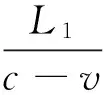
(1)

其中v为地球相对“以太系”的运行速度，c为光速，L1为透射光到反射镜M1的距离.对于反射光，如图1(b)所示，当时认为在以太系中光速为c，故在竖直方向上有分量，应有

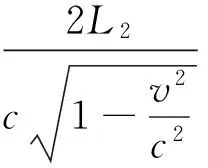
(2)

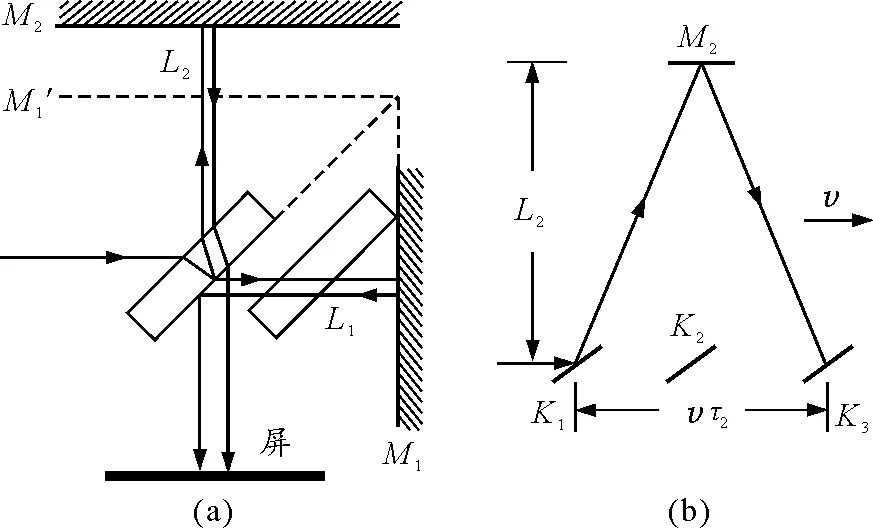
图1 实验光路图

考虑到补偿板已插入，两路光的光程差即为Δδ=c(τ1-τ2).装置旋转90°后光路情况交换，故光程差变化为2Δδ，实验中L1与L2取为11 m，若v大小取30 000 m/s，代入算式，旋转前后光程变化对应约0.37个波长，故应有0.37个条纹移动[2].

上述方法仅选择了中心位置进行分析，并未对其他近轴点进行一般分析，如此就可能产生疑问：“也许只有这中心点会有亮度改变，而旋转90°对中心附近点的亮度分布几乎没有影响，导致我们肉眼观察不到中心点的变化，所以才得出了零结果的结论？”或是：“是否因为旋转前装置与以太风恰成45°角，导致旋转90°后图样确实不会有变化？”诚然，从简单定量角度来看，该方法可最快给出结论，然而在未严格给出总体变化规律前，将零维特殊点的变化直接上升到二维难免有失严谨.

2 基于当时时空观的计算

我们可通过镜像法将整个光路化为两个点光源在观察屏上方成干涉图样的问题，如图2所示.

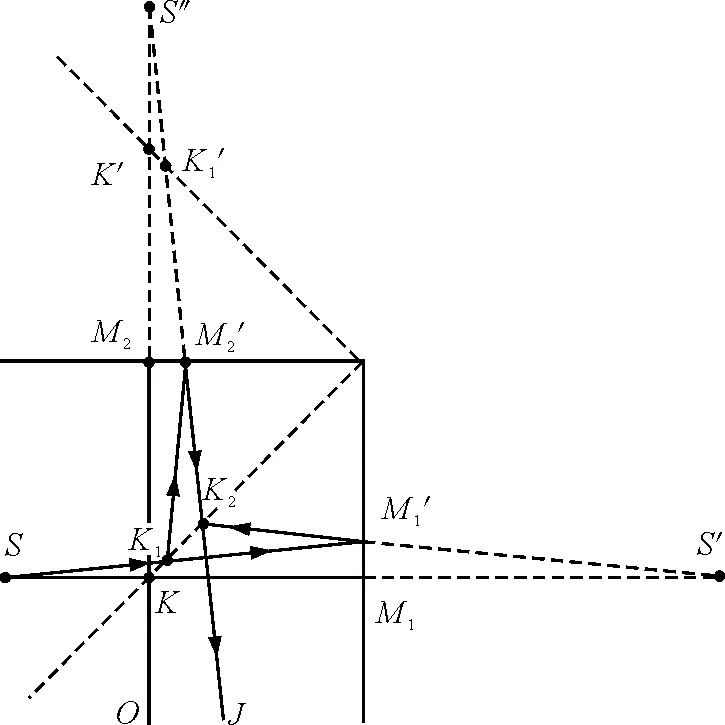
图2 迈克耳孙-莫雷实验的细化光路图

需要注意的是，由于经过了镜像处理，部分光路等效的v方向会发生改变，同时在装置旋转90°时，其变化方向也不相同，具体规律如表1所示(为不至于混乱，暂以两点光源重合于S″分析).

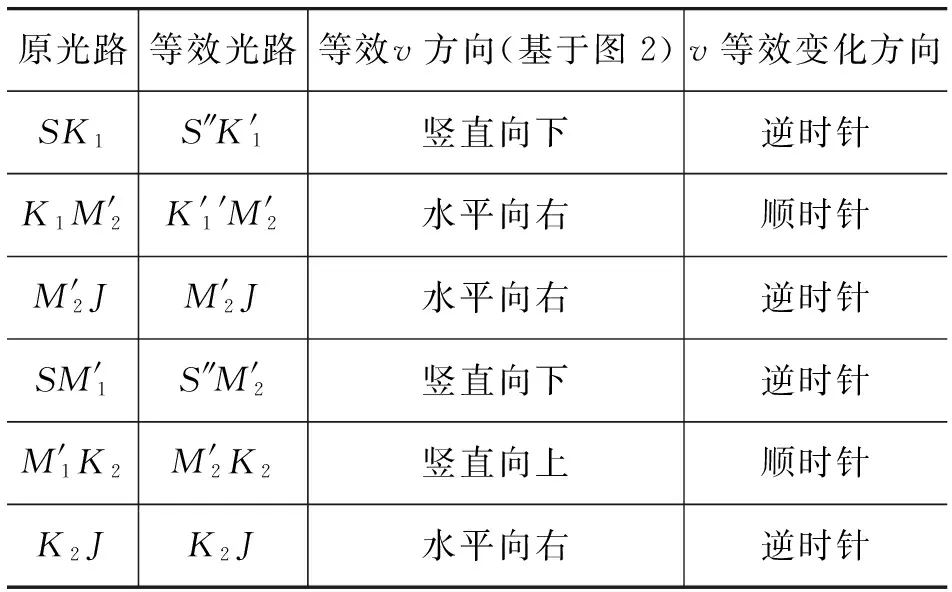
表1 等效光路理论变化情况

现不妨设L1与v所成夹角为α，此时由图3可知：光在“以太系”中的走向为K→M1→K2，只需使用余弦定理即可求出KM1的长度，即对应的实际光程.

由图3得

则其实际光程

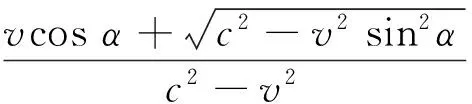
(3)

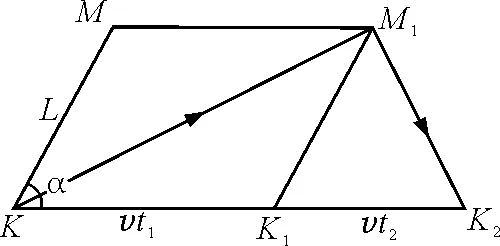
图3 实际光程理论示意图

由式(3)，只要知道某等效光线在“地球系”走过的长度L，及L与相对运动速度v所成的夹角α，便可得出在“以太系”下传播的实际光程.

继续计算各段的L与α.先来分析各段等效光路在“地球系”的传播长度L.对观察屏建立如图4所示的三维直角坐标系：定E点为坐标原点，x轴正方向与v同向，K→M2方向为z轴正方向.为方便计算，设

h=KEH=S″E=SK+2KM2+KE

(4)

图4 地球系下近轴光线的理论长度

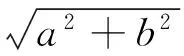
(5)

则各段长为

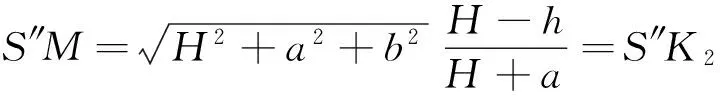
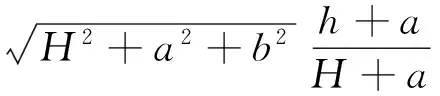
(6)

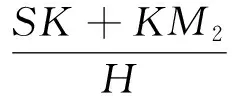
则

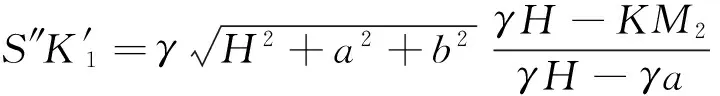
(7)

式中h*=K′E,至此各段长度均可表示.继续分析L与相对运动速度v所成夹角α的情况.如图5所示，假设等效v沿HC方向(可以证明v恒在xOz平面内)，HJ为地球系下观察到的光传播方向，故α=∠CHJ，应用两次余弦定理便可求出.先对△COJ分析

CJ2=H2tan2θ+a2+b2+2aHtanθ

(8)

在△CHJ中

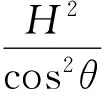
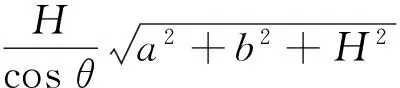
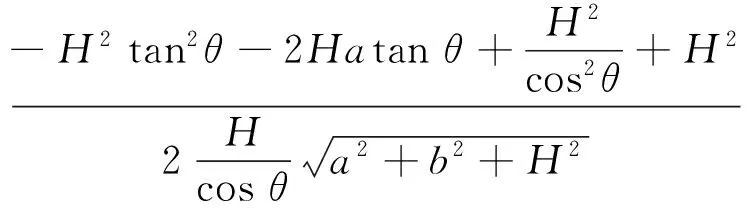
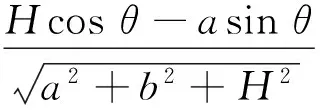
(9)

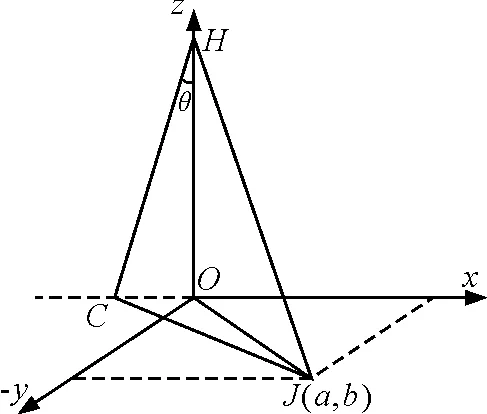
图5 夹角计算

同理，v指向x正半轴时

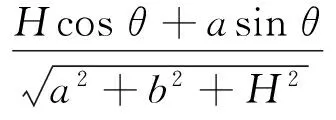
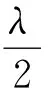
3 基于Matlab的模拟

理论计算完备后，便可进行模拟，本文使用Matlab2011b版本运算，并为保证运算速度，采样点选为28+1即257个.当实验光波长选择为590 nm,臂长取为11 m与11.001 m,观察屏半宽度0.8 m,分光板距观察屏15 m,相对速度v取地球公转速度30 000 m/s时，预期的不同角度下模拟图样应如图6所示.

图6 在上述条件下，转过不同角度时的预期图样

可以看出，干涉图样应有明显的变化，变化表现在条纹不断被“吞入”.外围的条纹逐渐向中心靠拢，越外圈的条纹移动程度越不明显.有了该变化规律，才能说用中心点来计算预期变化是可行的，同时上述一系列的疑问自然也就解开了.

4 结论补充

上文虽已给出了迈克耳孙-莫雷实验的预期模拟，但在实际中还存在着几个值得注意的问题，接下来从3个问题切入，并结合模拟来逐一分析.

(1)表述问题.在上文中已得出了理论上变化的规律，应是条纹“吞吐”的变化，而目前部分文章中表述为条纹的“移动”，移动是一个很模糊的描述，是需要避免的误区.

(2)臂长问题.在通过公式得出条纹变化条数时，我们常将L1与L2直接取为11 m,并得出0.37个条纹的结论.该步骤从物理意义角度来看并不妥当，假若两臂均取11 m,代入模拟并不能形成干涉条纹，因为两个等效光源重合为了一点.因此,本实验中臂长不等是产生现象的关键前提，当L1为11 m时,L2必须为11 m±δ，δ是不可消除误差，若不考虑该误差，列出的计算式没有对应的实际意义.从这一角度来看，实验中旋转的操作也不是为了“消除”臂长误差，主要是为交换两光路的传播方式.

图7 v取750 m/s时，转过角度后也几乎没有变化

(3)“零结果”问题.迈克耳孙-莫雷实验的结果在当时并没有完全否定以太的存在，迈克耳孙本是为了测量地球相对以太的运动速度，但最后不成想只观测到了极小的条纹变化，或才有了零结果这一说法.若我们在模拟中保持其他参数不变，将v修改

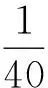
5 GUI模拟界面

利用Matlab软件自带的GUI功能生成一个模拟窗口(图8)，可快速调整各个参数的数值并观察其对图样的影响.本界面将旋转角度、相对以太速度、两臂长、屏宽这5个主要参数以滑块方式集合.

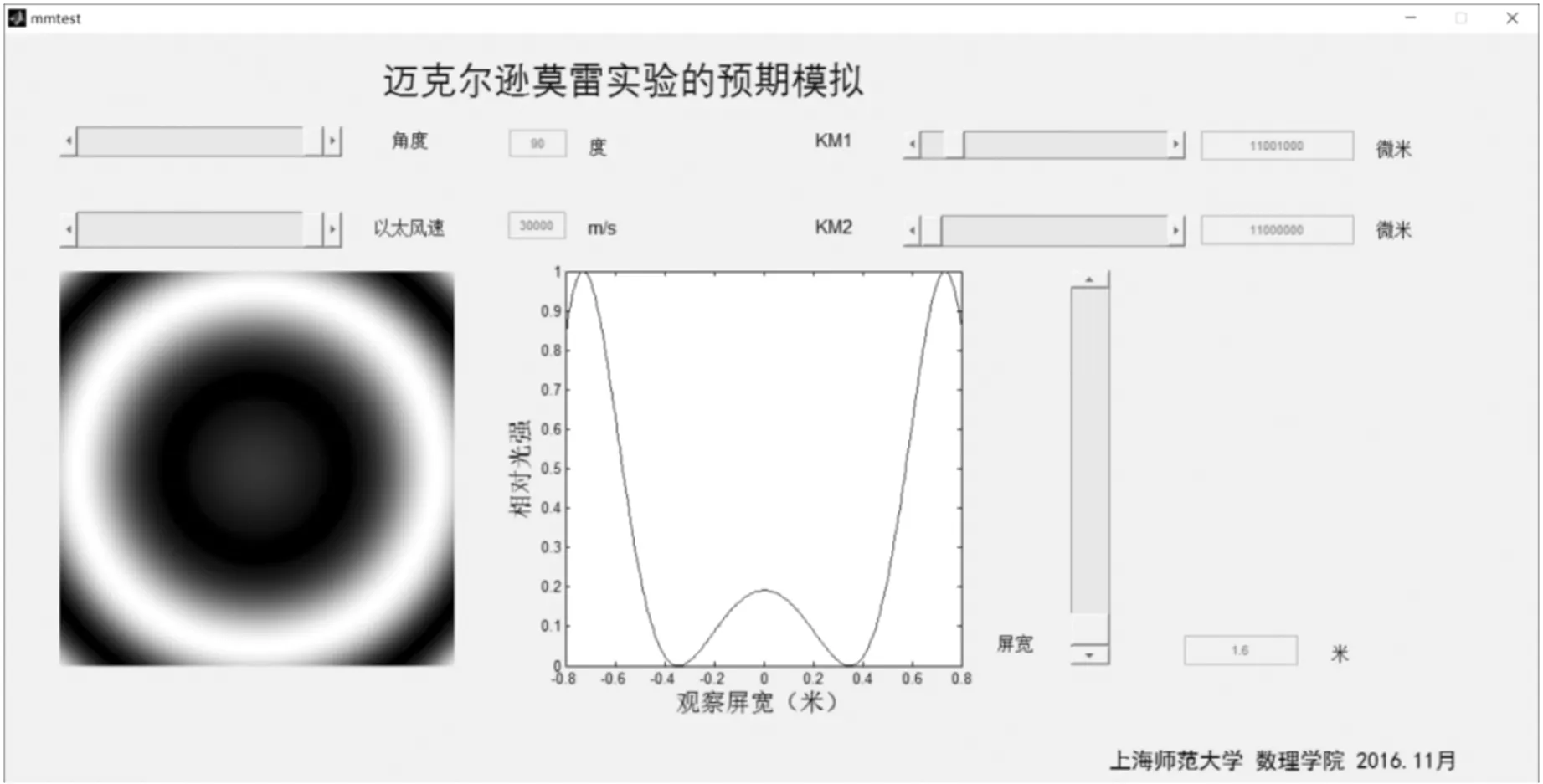
图8 迈克耳孙-莫雷实验的预期模拟GUI界面

1 曹天元.量子物理史话 上帝掷骰子吗.沈阳：辽宁教育出版社，2008.28～32

2 冯杰.大学物理专题硏究.北京：北京大学出版社，2011.291～297

3 漆安慎，杜婵英.力学(第2版).北京：高等教育出版社，2005.422～425

4 姚启钧.光学教程(第4版).北京：高等教育出版社，2008.42～44

2017-02-25)

潘尹凡(1994- )，男，在读硕士研究生，研究方向为物理学科教学.

指导教师：冯杰(1961- )，男，教授，硕士生导师,研究方向为理论物理、非线性光学、物理课程与教学论.