沟槽面湍流减阻数值评估方法

周健， 欧平,*， 刘沛清， 郭昊

1.中国航天空气动力技术研究院， 北京 100074

2.北京航空航天大学 航空科学与工程学院， 北京 100083

沟槽面湍流减阻数值评估方法

周健1， 欧平1,*， 刘沛清2， 郭昊2

1.中国航天空气动力技术研究院， 北京 100074

2.北京航空航天大学 航空科学与工程学院， 北京 100083

为解决雷诺平均Navier-Stokes (RANS)方法模拟沟槽面减阻的实际应用问题，受Wilcox对粗糙度模化方法的启发，通过深入分析k-ω剪切应力输运(SST)湍流模型近壁区ω值的作用效果，发现在黏性底层内增加壁面ω值可使对应近壁区的湍动能、湍流黏度、雷诺应力均减小，这种对近壁区流动特性的作用效果与真实沟槽面一致。以经典的对称V型沟槽面(高度=间距)减阻实验数据为基础，通过引入减阻效果影响因子——压力梯度与偏航角，建立复杂流动条件下沟槽面几何尺寸到壁面ω值的模化函数方程，将数值模拟结果与实验结果对比，验证了模化沟槽面可以达到与真实沟槽面相同的减阻效果，并依此给出沟槽面减阻在工程实践中的应用方法，以C919翼身组合体巡航构型为例，完成其沟槽面减阻的总体设计与评估。

沟槽面； 湍流减阻；k-ω剪切应力输运； 模化函数； 数值模拟

自从20世纪70年代NASA兰利研究中心发现具有顺流向微小沟槽的表面能有效地降低壁面摩阻，突破了表面越光滑阻力越小的传统思维方式以后，沟槽面减阻一直是湍流减阻技术中的研究焦点。Walsh等最先开展了平板沟槽面湍流减阻的研究[1-4]，天平测力结果表明最佳的减阻构型是一种对称V型沟槽面，当其高度h和间距s的无量纲尺寸为h+≤25和s+≤30时具有减阻特性，减阻效果最佳时沟槽面的尺寸为h+=s+=15。对于压力梯度影响的研究，Debisschop和Nieuwstadt[5]研究了逆压梯度对平板沟槽面的影响，得到了13%的减阻效果，比相应的零压梯度情形多减阻7%；Sundaram等[6]对0°～6° 迎角NACA0012翼型的沟槽面减阻研究表明，减阻效果随迎角的增加而增加，最大减阻值达到13%。对于亚声速流动，Viswanath和Mukund[7]对ADA-S1超临界翼型在马赫数0.70～0.76进行沟槽面减阻实验研究，得到了最大12%的减阻效果，且主要体现在翼型背风面。空中客车公司在A320试验机70%的表面贴上沟槽面薄膜，获得了节油1%～2%的效果[8]。国内对沟槽面减阻的研究相对较晚[9]，北京航空航天大学的兰世隆和王晋军[10]通过LDV技术对比了沟槽面及光滑面湍流边界层流速和湍流度分布，结果表明：与光滑面相比，沟槽面湍流边界层时均流速分布对数律公式中具有较大的常数C值，且近壁区沟槽面湍流度最大值较小，出现的位置距壁面较远。华南理工大学的黄德斌等[11]通过数值方法对比了V型沟槽面和T型沟槽面的减阻性能，最高达到9%的减阻效果，与Walsh等[1-4]早期对平板沟槽面的减阻效果相一致。

沟槽面减阻作为最热的减阻技术之一，虽被国内外学者广泛研究，但在这项技术的工程应用进展上，仍存在一些关键性问题。首先，目前能对湍流结构做出精确预测的数值方法只有直接数值模拟(DNS)和大涡模拟(LES)，这两种方法多用于沟槽面减阻机理的探讨，并且都是在小尺度、低雷诺数和简单流动下进行的，对于高雷诺数和复杂几何外形的实际应用问题，两种方法都无能为力；其次，由于数值模拟的局限性，使得实验研究带有一定的盲目性，且沟槽面减阻的效果表现在数值上是一个很小的量级，只有高精度的实验仪器才能测得较为准确的数据，这使得实验成本大大增加。1970年，Saffman[12]通过对k-ω系列湍流模型研究发现，壁面边界上的ω值在一定范围内可任意取，并且不会影响流场计算的合理性，而壁面阻力特性也随ω值的不同而改变。Wilcox[13]根据这一发现通过总结Nikuradse[14]实验数据，将粗糙度ks通过参数ω模化到壁面边界条件中，实现了不同粗糙表面阻力计算的数值模拟。受粗糙度模化思想启发，Benedetto和Renato[15]通过对k-ω剪切应力输运(SST)湍流模型的研究，首次提出将对称V型沟槽面(h=s)模化到壁面ω值的思路，但对很多细节未作详尽解释； Aupoix[16]以现有实验数据为基础，完成了对称V型和U型沟槽面基于S -A湍流模型和k-ω湍流模型壁面方程的模化，上述两种沟槽面模化方法都为简单的理论探讨，对于较复杂几何外形的应用问题则难以实现。

本文针对沟槽面减阻在工程上的应用问题，采用Wilcox粗糙度模化思想，将沟槽面视为一种特殊的粗糙度表面，从探索沟槽面减阻机理入手，通过深入分析k-ωSST湍流模型近壁区ω值对湍流结构的作用效果，结合现有实验数据建立不同流动条件下沟槽面物理构型尺寸到壁面ω值(即贴壁节点的ω值，ωw)的模化，消除对沟槽面物理构型直接建模进行数值模拟的困难，使得对沟槽面减阻在高雷诺数、复杂边界条件下的减阻效果评估变的可行。

1 沟槽面模化

1.1 k-ω SST湍流模型中壁面ω值的作用效果

在两方程涡黏湍流模型中，k-ε模型能够很好地模拟远离壁面充分发展的湍流流动，而k-ω模型则能很好地模拟各种压力梯度下的边界层流动问题。Menter[17]根据两种模型的特点，提出了k-ωSST两方程模型，它是一种在工程上得到广泛运用的混合模型，近壁区保留了原始的k-ω模型，远离壁面区则采用k-ε模型。

为完成沟槽面到壁面ωw的模化，首先研究k-ω模型中ω项对壁面阻力特性的作用机理。以不可压缩槽道湍流流动为例，k-ω模型封闭方程简化如下：

1) 湍流黏度

(1)

2)k方程

(2)

3)ω方程

(3)

式中：U为速度;y距离;α、α*、β*、β0、σ和σd均为常数；ν为黏度。k方程与ω方程等号右侧依次为产生项、耗散项、黏性扩散项、对流项，ω方程最后一项为修正项。内区从壁面开始依次为黏性底层(y+<5～10)、过渡区(5～1030)，外区就是主流区也称为尾迹区。在黏性底层内，两方程中耗散项和扩散项平衡，进一步简化为

1)k方程

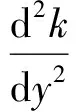
(4)

2)ω方程

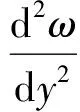
(5)

由湍流黏度定义-〈u′v′〉=νT·dU/dy可知，雷诺应力-〈u′v′〉也随νT的减小而减小，如图2所示，在等切应力层内，总切应力近似等于壁面切应力，而在对数层(y+>30)中，忽略分子黏性力小量，总切应力近似等于雷诺切应力-ρ〈u′v′〉，雷诺切应力的减小会导致壁面切应力的减小。即通过增大黏性底层内ωw值可以达到壁面摩阻减小的效果，并且这与真实沟槽面对近壁区的作用效果相一致[18]。另外，大量实验和DNS数据表明[19-21]，沟槽面减阻体现在近壁区平均流动特性上为对数区上移，这也将在下面算例验证里体现。

图1 ω增大对近壁区湍动能k和湍流黏度ν的影响
Fig.1 Influence of increase of ω on k and ν near wall

图2 近壁区雷诺切应力分布
Fig.2 Distribution of Reynolds shear stress near wall

1.2 沟槽面模化思路

采用雷诺平均Navier-Stokes (RANS)方法对沟槽面减阻进行复杂流动状态下的数值模拟，存在2个关键性问题。第一，由于沟槽面的减阻机理是改变了近壁处的湍流结构，而RANS方法将流场中的湍流脉动进行了平均化，这样很难模拟出沟槽面对近壁湍流结构的影响；第二就是建模与网格问题，由于沟槽面的尺寸非常小，对于高雷诺数复杂边界的计算构型，要想模拟出沟槽面对流动的影响，网格需要非常细密，建模和计算的成本太大。为避开上述2个问题本文采用Wilcox在数值模拟中对粗糙度的模化思路。

Wilcox[13]通过Nikuradse实验数据给出了k-ω系列湍流模型，粗糙度到壁面ω值的模化形式为

(6)

首先，根据现有实验数据，以研究最为广泛的V型对称沟槽面(h=s)为例，建立减阻百分比ΔCD%关于沟槽面无量纲尺寸h+和s+的函数关系：

(7)

其次，用光滑平板代替沟槽面数值模拟上述实验，通过改变壁面ωw值得到相应减阻百分比ΔCD%，获得函数关系：ωw=f2(ΔCD%)。将f1代入f2，便得到沟槽面无量纲尺寸的最终模化函数形式为

(8)

1.3 沟槽面模化形式

1) 零压力梯度平板

沟槽面无量纲尺寸到壁面ωw值的模化就是完成函数式(8)中f1与f2的确定。首先，以V型沟槽面(h=s)构型为研究对象，对经典的Walsh[22]平板沟槽面减阻实验数据进行二次多项式拟合，如图3所示。选择此类构型沟槽面主要考虑原因如下：沟槽面模化方法模化前依赖于现有可参考的实验数据，模化后需要更多实验数据进行算例验证，对称V型沟槽面(h=s)被研究最广泛，减阻效果较为明显，实验数据较为全面。

可以看出，在较优减阻范围内，拟合曲线与实验数据误差很小，得到f1的函数关系式为

ΔCD%=0.048 2(h+)2-1.216 7h++1.162 9

(9)

图3 Walsh沟槽面减阻实验数据拟合曲线
Fig.3 Fitting curve of experimental data by Walsh drag reduction with riblets

(10)

综合上述结果，得出零压力梯度平板模化参数ωw的最终函数形式为

lg(ωw/ω0)=(-ΔCD/a)1/b

(11)

2) 压力梯度β的引入

大量研究发现，逆压梯度对沟槽面减阻效果有较大的影响，并已证实逆压梯度下沟槽面的减阻效果比零压梯度更优，但由于其作用机理不清楚，不同学者研究结果存在差异，没有充足的实验数据可供研究分析，本文参考经典文献[5]的实验数据，给出减阻效果随压力梯度变化的大致规律。针对平板构型，实验分别研究零压与逆压梯度β=2.2时沟槽面的减阻效果，β=(δ*/τw)(dp/dx)，δ*为位移厚度，τw为壁面切应力，p为压力，如图6 所示。实验结果发现两种压力梯度下，不同无量纲尺寸沟槽面的减阻效果都存在相一致的2.65倍的系数关系。

图4 不同壁面下壁面ωw值与减阻效果的关系Fig.4 Relation between ωw and drag reduction effection in different of wall

图5 参数a和b随壁面变化Fig.5 Variation of parameters a and b with

图6 压力梯度对沟槽面减阻的影响
Fig.6 Influence of pressure gradient on drag reduction with riblet

对于V型对称沟槽面(h=s)，假设存在一个简单的线性关系f(β)，使得逆压梯度β下沟槽面的减阻效果ΔCDβ与相应尺寸零压力梯度的减阻效果ΔCD存在如下关系：

ΔCDβ=f(β)·ΔCD

(12)

满足

得到f(β)的函数表达式为

f(β)=0.75β+1

(13)

3) 偏航角φ的引入

实验中沟槽面槽道的分布方向可分为3种：顺流向、横向以及与流向呈一定角度方向。大部分实验都是顺流向分布，这种分布减阻也被认为效果最佳。Gaudet[23]发现沟槽面在流向呈一定角度时仍具有减阻效果，当该角度超过30° 时减阻效果消失；Coustols[24]通过实验验证了当沟槽面的偏航角φ≤20°时仍有较好的减阻效果。由于没有更多的实验数据，本文假设减阻效果与偏航角的正弦值存在简单的线性关系：

ΔCDφ=(aφsinφ+bφ)ΔCD

(14)

式中:ΔCDφ为偏航角φ下的减阻效果，满足

解得ΔCDφ的表达式为

ΔCDφ=(-2sinφ+1)ΔCD

(15)

1.4 沟槽面模化最终表达式

对于平板沟槽面减阻构型，考虑压力梯度与偏航角的影响，总体减阻百分比表达式为

ΔCDφβ=f(β)(aφsinφ+bφ)ΔCD

(16)

代替式(11)中的ΔCD便得到压力梯度下模化沟槽面的最终表达式为

ωw=ω0pow(10,(-ΔCDφβ/A)1/B)

(17)

式中：pow(A,B)为A的B次方。

对于存在曲率非零的减阻构型，如翼型和机翼等，不但有逆压梯度的存在，同时还有表面曲率的变化。Sundaram等[6]对NACA0012翼型0°～6° 迎角下沟槽面的减阻效果进行分析研究，实验结果发现6° 迎角下，上翼面的平均压力梯度β=1.06，达到13%的减阻效果，所以，曲率对沟槽面减阻效果也有较大的影响。由于本文沟槽面模化依赖于现有实验数据，而对于逆压梯度与偏航角对沟槽面减阻效果的影响尚无充足的实验数据提供全面支持，因此本文在现有数据基础上，通过分析两者对减阻效果的影响规律，提出合理的假设，获得模化沟槽面的最终函数表达式。

1.5 沟槽面模化的应用方法

从1.4节最终函数表达式中可以看出，它是沟槽面无量纲尺寸h+与壁面ωw值的关系，而对于沟槽面减阻的实际应用，在数值计算之前，由于无法通过沟槽面的绝对尺寸h获得其无量纲尺寸h+，必须利用参考模型(光滑)的计算结果进行无量纲化，同时，压力梯度β以及最终的减阻效果评估都需要参考模型的计算结果。数值模拟沟槽面减阻实际应用的具体步骤如下：

2) 以最优减阻尺寸h+=10～15为目标，通过参考模型计算结果，根据关系式h=h+μ/ρuτ确定最优沟槽面尺寸h分布，无量纲化后结合参考模型计算所得的各个参数，得到对应的沟槽面分布区壁面ωw分布。

3) 数值计算模化沟槽面下减阻构型的阻力特性，与参考构型进行对比分析，评估其减阻效果。

2 数值验证与分析

2.1 槽道流动

由减阻机理可知，沟槽面通过改变近壁区的湍流结构，达到减阻的效果，为进一步研究模化沟槽面对近壁区湍流结构的影响，分析了槽道流动下模化沟槽面的作用效果，并与DNS结果和实验结果对比分析。

Choi等[21]的DNS流场计算域如图7所示，Lx1为槽道长度，基于槽道对称轴速度Ul与半槽宽δ的雷诺数Re=4 200，基于平板面摩擦速度uτ的雷诺数Reτ=180，沟槽面尺寸h=s=0.113 5δ。

采用本文模化沟槽面代替沟槽面物理构型，计算得到沟槽面无量纲尺寸h+=20.43(文献[21]为20)。减阻效果如表1所示。模化沟槽面的减阻百分比与Walsh[3]实验数据基本一致(压力梯度β=0)，但与DNS结果有所差异，可能的原因是文献[21]引入了压力梯度因素。

为进一步研究模化沟槽面对近壁流动结构的影响，对比近壁区平均速度U+剖面，如图8所示。可以看出k-ωSST与DNS的平板面计算结果在黏性底层到对数层的过渡区存在差异，但在对阻力值影响较大的对数区，两者基本一致，满足对数律关系。大量槽道流动实验已表明，不同阻力特性壁面近壁区无量纲速度剖面有相同的斜率1/κ和不同的截距C，C值越大，摩阻相对越小。由表1可知，本文模化沟槽面的减阻效果不及DNS，所以沟槽面的C值小于DNS计算结果，但大于平板C值。

图7 DNS槽道计算域
Fig.7 DNS channel computational domain

表1 减阻效果对比Table 1 Comparison of drag reduction effection

图8 近壁区平均速度剖面对比
Fig.8 Comparison of average velocity profiles near wall

图9为模化沟槽面与平板近壁区雷诺切应力变化对比。可以看出，模化沟槽面近壁区雷诺应力减小，在h+=20处，相对减小值为6.4%。这一变化规律与DNS结果基本一致，说明本文沟槽面模化方法在对近壁湍流流动作用效果上与真实沟槽面相符，可以用于后续的数值研究。

图9 雷诺切应力分布对比
Fig.9 Comparison of Reynolds shear stress distribution

2.2 翼型绕流

翼型既存在压力梯度又存在曲率变化，通过对NACA0012翼型与GAW(2)翼型的沟槽面减阻进行数值模拟，并与实验结果对比，确定翼型曲率情况下，模化沟槽面的表达形式，并对计算结果进行对比分析。

2.2.1 NACA0012翼型

弦长c=0.6 m，来流速度U=30 m/s，雷诺数Re=106。在其上下表面0.12c～0.96c间布置h=0.152 mm的对称V型沟槽面(h=s)，翼型与沟槽面分布如图10所示。

采用结构网格O型划分，第一层网格绝对高度设为0.01 mm，对光滑表面翼型进行计算得到贴壁节点y+<1，处于黏性底层内。对各迎角下光滑翼型进行数值模拟，通过壁面摩擦速度uτ分布得到沟槽面无量纲尺寸h+沿翼型上表面分布，如图11所示。与实验值对比，在翼型前缘计算结果偏大，分析可能的原因为实验中转捩带的存在使得前缘壁面边界层厚度增加，从而表面摩阻相应减小，但是两者都处于沟槽面最优减阻尺寸范围内，阻力计算结果可信度较高。图12为不同迎角下翼型上表面逆压梯度沿弦向的变化与弦长0.4c～0.9c逆压梯度平均值和实验结果对比。

图10 NACA0012翼型与沟槽面分布
Fig.10 Distribution of riblets on NACA0012 airfoil

图11 上翼面沟槽面无量纲尺寸h分布
Fig.11 Distribution of riblets h on airfoil upper surface

图12 翼型上表面压力梯度的平均值
Fig.12 Mean value of pressure gradient on airfoil upper surface

为确定翼型曲率对沟槽面减阻效果的影响与模化沟槽面的函数表达式，仍假设f(β)=aβ+1，a为待定参数。首先，为取消压力梯度因子的介入，数值模拟f(β)=1时各迎角下模化沟槽面的减阻效果ΔCD；结合实验数据，根据式(12)，得到f(β)的表达式为

f(β)=ΔCDβ/ΔCD=2.15β+1

(18)

如图13所示，f(β)线性表达式斜率由平板时的0.75变为2.15，可见翼型表面曲率对沟槽面减阻效果的影响很大。将上述f(β)代入模化沟槽面最终形式对NACA0012翼型进行数值模拟，计算结果与实验结果对比如图14所示，表达式斜率为2.15时与实验结果吻合度较高，对翼型或者机翼这样曲率变化较大的表面，国内外几乎没有专门的研究工作，对沟槽面减阻效果的预测更加困难。

图13 f(β)线性拟合曲线
Fig.13 Linear fitting curve of f(β)

图15为不同迎角不同参考位置处翼型表面近壁区法向速度u剖面。首先，模化沟槽面下对数区上移，与真实沟槽面作用效果一致；其次，通过对比可见逆压梯度对沟槽面减阻效果影响明显，在没有流动分离情况下，正迎角翼型上表面后缘逆压梯度较大，减阻效果较为明显(图15(a)～图15(c))；而翼型下表面为顺压梯度，减阻效果不明显(图15(d))。

图14 逆压梯度与表面曲率对减阻效果的影响
Fig.14 Influence of pressure gradient and surface curvature on drag reduction effection

图15 翼型表面法向速度剖面
Fig.15 Normal velocity profiles on airfoil surface

2.2.2 GAW(2)翼型

GAW(2)翼型是一种常见的通用航空翼型，最大厚度为13%，与NACA0012翼型相差不大，曲率分布差异主要体现在下表面后缘。在上下表面0.12c～0.96c处布置尺寸h=0.076 mm和h=0.152 mm 两种V型沟槽面(h=s)，如图16所示。

由NACA0012翼型计算结果可知，表面曲率对减阻效果影响较大，鉴于两翼型厚度和上表面曲率分布差异不大，对压力梯度进行模化时仍采用表达式f(β)=2.15β+1。减阻效果计算结果与实验对比如图17所示[25]。可见，该表达式对两种翼型都能达到较理想的减阻预测效果。

图16 GAW(2)翼型与沟槽面分布
Fig.16 Distribution of riblets on GAW(2) airfoil

图17 减阻效果与实验结果对比
Fig.17 Comparison of drag reduction effection with experimental data

3 C919翼身组合体沟槽面减阻设计与评估

参照空客A320沟槽面减阻布局设计[8]，对C919无发动机短舱干净翼身组合体构型在机身等直段与主翼的上下表面进行沟槽面分布设计与减阻评估。

3.1 数值计算模型

C919翼身组合体半模的三维几何构型与结构网格划分如图18所示，网格总数约为550万。巡航高度为10 km，当地标准大气压为2.642×104Pa，温度为223.15 K，计算来流马赫数Ma=0.785，基于来流速度和机翼平均气动弦长的雷诺数Re=2.68×107，迎角为0°、1°、1.5°。

图18 翼身组合体结构网格
Fig.18 Mesh on wing-body combination structure

3.2 沟槽面设计

以无量纲沟槽面最优减阻尺寸h+=12为基准，由关系式h+=uτh/ν可知，每一个uτ/ν值都对应一个沟槽面的绝对尺寸h，这样一个变尺寸的沟槽面在工程应用中显然是不可能做到的。图19 为0° 迎角翼身组合体表面沟槽面最优减阻尺寸分布，可见，最优尺寸在机身等直段表面分布变化不大，在沟槽面分布区域可用其平均值作为最优减阻尺寸；而机翼表面沟槽面最优尺寸分布变化较大，由前缘到后缘最优尺寸逐渐增大。

图19 翼身组合体表面沟槽面理论最优减阻尺寸h分布云图
Fig.19 Cloud of optimal riblets drag reduction h on wing-body combination surface

对于翼身组合体表面压力梯度影响因子f(β)的处理，由于机翼截面翼型与GAW(2)曲率分布相似，取f(β)=2.15β+1作为机翼外表面沟槽面模化压力梯度方程；机身等直段表面曲率变化不大，可按无曲率平板情况对待，取f(β)=0.75β+1作为机身沟槽面模化压力梯度方程。

对于沟槽面最优尺寸在机翼表面分布，做以下两种设计方案：① 从简易性考虑，用机翼上下表面沟槽面分布区最优尺寸理论平均值作为各自最优设计尺寸；② 观察图19理论最优尺寸在机翼表面分布，可沿流向分两个区域设计沟槽面最优尺寸，如图20所示，每个区域理论平均值作为沟槽面最优设计尺寸。

图20 机翼表面最优沟槽面尺寸设计分布
Fig.20 Distributions of optimal riblets size on wing surface

3.3 计算结果

对0°、1°、1.5° 迎角下2种沟槽面设计方案进行数值模拟，对比阻力系数变化如表2所示。可见，两种方案沟槽面均能达到2%～3%左右的减阻效果，方案2略优于方案1；总的减阻效果都随迎角的增加而减弱。

表2 两种分布方案的减阻效果Table 2 Drag reduction effection of two distribution plans

4 结 论

本文通过深入分析k-ωSST湍流模型近壁湍流参数ω对壁面阻力特性的影响，结合现有实验数据，完成了沟槽面物理构型到壁面ωw值的模化方法与具体模化形式，并给出工程实践中沟槽面减阻的设计与评估方法。

1) 通过研究分析壁面k方程与ω方程的作用效果发现，在黏性底层内，壁面ωw值的增加使得近壁区湍流结构重新分布，从而导致壁面切应力的减小。且这种对近壁湍流结构的作用效果与真实沟槽面有很好的一致性。

2) 通过沟槽面翼型绕流算例，验证了本文沟槽面模化方法能够预测减阻效果随逆压梯度的变化规律，可对沟槽面在高雷诺数、复杂几何边界构型的减阻效果作出初步评估。

本文给出的沟槽面数值模化结果依赖于现有可靠的实验数据，由于实验数据的不充分，对逆压梯度、偏航角、表面曲率的模化尚处于合理假设阶段，这也是本文研究存在的不足之处。

[1] HEFNER J N, BUSHNEL D M, WALSH M J. Research on non-planar wall geometries for turbulence control and skin-friction reduction[C]//8th U.S.-FRGDEA-Meeting, 1983： 1-10.

[2] WALSH M J. Riblets as a viscous drag reduction technique[J]. AIAA Journal, 1983, 21(4): 485-486.

[3] WALSH M J. Turbulent boundary layer drag reduction using riblets： AIAA-1982-0169[R]. Reston: AIAA, 1982.

[4] WALSH M J, LINDEMANN A M. Optimization and application of riblets for turbulent drag reduction： AIAA-1984-0347[R]. Reston: AIAA, 1984.

[5] DEBISSCHOP J R, NIEUWSTADT T M. Turbulent boundary layer in an adverse pressure gradient-effectiveness of riblets[J]. AIAA Journal, 1996, 34(5): 932-937.

[6] SUNDARAM S, VISWANATH P R, RUDRAKUMAR S. Viscous drag reduction using riblets on NACA0012 airfoil to moderate incidence[J]. AIAA Journal, 1996, 34(4): 676-682.

[7] VISWANATH P R, MUKUND R. Turbulent drag reduction using riblets on a supercritical airfoil at transonic speeds[J]. AIAA Journal, 1995, 33(5): 945-948.

[8] COUSTOLS E, SCHMITT V. Synthesis of experimental riblet studies in transonic conditions[C]//Turbulence Control by Passive Means. Netherlands: Springer, 1990: 123-140.

[9] 王晋军． 沟槽面湍流减阻研究综述[J]． 北京航空航天大学学报， 1998， 24(1)： 31-34.

WANG J J. Reviews and prospects in turbulent drag reduction over riblets surface[J]. Journal of Beijing University of Aeronautics and Astronautics， 1988, 24(1): 31-34 (in Chinese).

[10] 兰世隆， 王晋军． 沟槽面与光滑面湍流边界层特性比较[J]． 实验力学， 1998， 13(1)： 28-33.

LAN S L, WANG J J. Experimental comparison between the turbulent boundary layers for corrugated and flat surfaces[J]. Journal of Experimental Mechanics， 1998, 13(1): 28-33 (in Chinese).

[11] 黄德斌， 邓先和， 王杨君． 沟槽面管道湍流减阻的数值模拟研究[J]． 水动力学研究与进展， 2005， 20(1)： 101-105.

HUANG D B, DENG X H, WANG Y J. Numerical simulation study of turbulent drag reduction over riblet surfaces of tubes[J]. Journal of Hydrodynamics, 2005, 20(1): 101-105 (in Chinese).

[12] SAFFMAN P G. A model for inhomogeneous turbulent flow[J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 1970, 317(1530): 417-433.

[13] WILCOX D C. Turbulence modeling for CFD[M]. 2nd ed. California: DCW Industries, 1998: 180-195.

[14] NIKURADSE J. Laws of flow in rough pipes: NACA-TM-1292[R]. Washington, D.C.: NASA, 1950.

[15] BENEDETTO M, RENATO T. Numerical simulation of riblets on airfoils and wings: AIAA-2012-0861[R]. Reston: AIAA, 2012.

[16] AUPOIX B, PAIHAS G, HOUDEVILLE R. Towards a general strategy to model riblet effects[J]. AIAA Journal, 2012, 50(3): 708-716.

[17] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 269-289.

[18] 胡海豹， 宋保维， 刘占一, 等． 沟槽面表面边界层湍动能分布规律[J]． 航空学报， 2009， 30(10)： 1823-1828.

HU H B, SONG B W, LIU Z Y, et al. Research on characteristics of turbulence kinetic energy in boundary layer over riblet surfaces[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1823-1828 (in Chinese).

[19] 李山， 杨绍琼， 姜楠． 沟槽面湍流边界层减阻的TRPIV测量[J]． 力学学报， 2013， 45(2)： 183-192.

LI S, YANG S Q, JIANG N. TRPIV measurement of Drag-reduction in the turbulent Boundary layer over riblets plate[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 183-192 (in Chinese).

[20] GOLDSTEIN D, HANDLER R, SIROVICH L. Direct numerical simulation of turbulent flow over a modelled riblet covered surface[J]. Journal of Fluid Mechanics, 1995, 302: 333-376.

[21] CHOI H, MOIN P, KIM J. Direct numerical simulation of turbulent flow over riblets[J]. Journal of Fluid Mechanics, 1993, 255: 503-539.

[22] WALSH M J. Riblets[C]//Viscous Drag Reduction in Boundary Layers, 1990: 203-261.

[23] GAUDET L. An assessment of the drag-reduction properties of riblets and the penalties of off design conditions[R]. 1987.

[24] COUSTOLS E. Behavior of internal manipulators: ‘riblet’ models in subsonic and transonic flows: AIAA-1989-0963[R]. Reston: AIAA, 1989.

[25] SUBASCHANDAR N, KUMAR R, SUNDARAM S. Drag reduction due to riblets on a GAW(2) airfoil[J]. Journal of Aircraft, 2012, 36(5): 890-892.

Numericalevaluationmethodofturbulencedragreductionwithriblets

ZHOUJian1,OUPing1,*,LIUPeiqing2,GUOHao2

1.ChinaAcademyofAerospaceAerodynamics,Beijing100074,China2.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China

InordertoapplynumericalsimulationmethodbasedonReynolds-averagedNavier-Stokes(RANS)equationstodragreductionwithriblets,inspiredbytheroughnessmodel-Wilcoxandafteradeeperstudyontheeffectofthevalueofωnearwallink-ωshearstresstransport(SST)turbulencemodel,itturnsoutthatanincreasingofwallωinviscoussublayerleadstoadecreasingofturbulentkineticenergy,turbulentviscosityandReynoldsshearstress,whichshowsthesamechangeasrealisticriblets.BasedontheclassicalexperimentaldataofribletswithsymmetricVgrooves(height=width),byintroducingtheeffectfactorspressuregradientsandyawangle,amodelingfunctionbetweenribletsgeometrysizeandthevalueofwallωisestablishedincomplexflowconditions.Comparingwiththeexperimentaldataconfirmsthatthemodelingribletscanpredictthedragreductionasrealisticriblets.Besides,adetailedapplicationmethodofmodelingribletsisproposed.Atlast,anoveralldesignandevaluationofthedragreductionbyribletsisgiveninthecaseoftheC919wing-bodycombination.

riblet;turbulencedragreduction;k-ωshearstresstransport;modelingfunction;numericalsimulation

2016-03-25；Revised2016-09-20；Accepted2016-09-26；Publishedonline2016-09-280927

URL：www.cnki.net/kcms/detail/11.1929.V.20160928.0927.004.html

.E-mailcaaaop@163.com

2016-03-25；退修日期2016-09-20；录用日期2016-09-26； < class="emphasis_bold">网络出版时间

时间：2016-09-280927

www.cnki.net/kcms/detail/11.1929.V.20160928.0927.004.html

＊

.E-mailcaaaop@163.com

周健， 欧平， 刘沛清， 等． 沟槽面湍流减阻数值评估方法J． 航空学报,2017,38(4):120263.ZHOUJ,OUP,LIUPQ,etal.NumericalevaluationmethodofturbulencedragreductionwithribletsJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):120263.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0263

V211； O357.5； TK89

A

1000-6893(2017)04-120263-12

(责任编辑： 李明敏)