小型无人机气动参数辨识的新型HGAPSO算法
邵干, 张曙光,2,3,*, 唐鹏
1.北京航空航天大学 交通科学与工程学院, 北京 100083
2.飞机/发动机综合系统安全性北京市重点实验室, 北京 100083
3.先进航空发动机协同创新中心, 北京 100083
4.北京航空航天大学 能源与动力工程学院, 北京 100083
小型无人机气动参数辨识的新型HGAPSO算法
邵干1, 张曙光1,2,3,*, 唐鹏2,3,4
1.北京航空航天大学 交通科学与工程学院, 北京 100083
2.飞机/发动机综合系统安全性北京市重点实验室, 北京 100083
3.先进航空发动机协同创新中心, 北京 100083
4.北京航空航天大学 能源与动力工程学院, 北京 100083
针对小型无人机(UAVs)研制中操稳特性和飞行控制律设计评估对气动参数辨识的需求,提出了一种混合遗传粒子群优化算法(HGAPSO)。该算法以粒子群优化算法(PSO)为主体,在粒子优化路径中,引入遗传算法(GA)的交叉变异操作,增强粒子群跳出局部最优的能力;同时采用Kent映射改进粒子种群的初始化,使初始种群在可行解空间内分布更加均匀,增强全局优化能力。基于仿真结果,依据辨识准度及辨识成功率,对比了HGAPSO、常规PSO和GA优化算法气动参数辨识的结果,然后用蒙特卡洛仿真测试随机观测噪声的影响,结果表明该算法兼备PSO算法高的搜索效率和GA算法的全局优化能力,对随机观测噪声不敏感。最后,通过设计小型UAV试飞示例进行综合应用评价,结果表明:HGAPSO算法基于真实试飞数据进行气动参数辨识取得了满意结果,具有良好的实用性。
小型无人机; 气动参数; 参数辨识; 混合遗传粒子群优化算法(HGAPSO); 搜索效率; 全局优化
近年来小型无人机(UAV)技术正快速发展。与有人驾驶飞机相比,UAV具有不受载人限制、尺寸小、成本低等一系列优点,在航拍、地图测量、植保、军事侦察等军用和民用领域市场需求越来越大。飞行控制系统是UAV实现上述任务的核心部件,而设计的基础是获得可预测UAV运动特性的描述模型及其气动参数。
一般获得气动参数的方法主要有风洞试验、计算流体力学(CFD)计算和飞行辨识试验等。多年来,风洞试验数据一直是新研飞行器气动参数的最主要来源,然而风洞试验本身有其固有的局限性,例如缩比相似性、支架和洞壁干扰等问题,无法完全模拟真实飞行环境,且风洞试验需经过多次修正,周期长,费用昂贵[1]。CFD计算具有相对高效、低成本等优势,但其计算结果的精准度往往需要试验校验[2]。直接基于飞行试验辨识气动参数和动力学特性,更加接近真实物理系统[3-4],也是对风洞试验和CFD结果进行校验的重要手段。对于小型UAV,其具有制作和试验成本低的优势,直接利用飞行辨识得到气动参数从精度、适用性和成本等各个方面都能很好地满足小型UAV的需求[5-7]。
气动参数辨识目前已发展了多种辨识方法,包含广义卡尔曼滤波、极大似然法、分割算法等,其中应用最为广泛的就是基于极大似然法发展的一系列辨识算法[8],如方程误差法(EEM)、输出误差法(OEM)以及滤波误差法(FEM)等[9-10]。基于极大似然法的这些辨识方法取得了很多成功经验,但一般都需要求解雅克比矩阵或海森矩阵,要求搜索空间内连续可微。由于需要计算导数,算法对于系统噪声和野值比较敏感,在强噪声和野值存在的情况下可能会导致算法失效。另外,多极值时的局部性、矩阵奇异时的求解、对初值依赖等问题,也需要克服。对于小型UAV可能面临更大的测量噪声环境,原因在于其较小的重量和尺寸导致更快的响应动态(运动频率更高),对突风等各类飞行干扰相对于大型飞机更加敏感,而且传感器成本控制等实际因素也易引入附加测量噪声。因此,需要发展一类不依赖于导数求取、对初值不敏感的辨识方法。
遗传算法(GA)、粒子群优化算法(PSO)等群体进化算法则提供了克服以上缺点的一条途径。进化算法一般通过适用度同时比对全局多个点,对初值依赖较小,具有高效的全局优化能力。另外,由于寻优是在整个数据段上,而不是利用梯度信息修正的方法,不要求计算导数,所以对噪声和野值的敏感小,在强噪声下仍然能够获得很好的收敛特性。Burchett[11]对比了基于梯度的算法和以GA为代表的进化算法进行气动参数辨识的效果,表明进化算法的辨识效果更好。钱炜祺[12]、张天姣[13]等先后利用GA、PSO完成了飞机和导弹的气动参数辨识,表明GA、PSO可以有效解决梯度类优化算法依赖初值、局部最优解以及对噪声敏感的问题。
GA和PSO作为进化算法,存在许多相似之处,但是其算法思想和具体实现方式的不同,使得它们各具特点[14]。GA通过交叉和变异跳出局部,具有良好的全局搜索能力,但其局部搜索能力较差,导致单纯GA比较费时,在进化后期搜索效率低。PSO具有全局信息共享机制,所有粒子都向整个种群的最优值移动,能够迅速找到全局最优,但也导致粒子群算法进行到后期容易陷入局部极小。因此,将二者相结合并充分发挥二者优点,提升全局搜索能力和快速收敛能力是当前研究热点,主要方法是在种群更新时,先用GA和PSO中的一种对粒子进行优化,接着用另一种方法优化粒子路径。Ibrahim和Selamat[15]先对一部分粒子用PSO更新,更新后的粒子与未变化的粒子一起进行交叉变异;Huang[16]提出对种群全体位置进行交叉变异之后,直接应用PSO对全体粒子更新;Shama和Singhal[17]对一半的种群进行交叉变异操纵,然后采用PSO算法更新种群全体。这些算法基本上是天然的将GA与PSO进行融合,且GA占据较大的参与度,虽然保留GA较强粒子跳出局部最优的能力,但同时也降低了优化效率,且面对不同的问题,GA和PSO各自的权重保持不变,不利于算法更广的实用性。
本文基于上述考虑,寻求具备较高的搜索效率和全局优化能力方法,提出了一种新的GA和PSO融合方式,同时对进化算法所共有的种群初始化问题进行改进,并将其应用到小型无人机的气动参数辨识中。
1 改进的混合遗传粒子群优化算法
1.1 遗传算法(GA)和粒子群算法(PSO)基础
GA是一种模拟生物进化论的优化算法[18]。基本的GA包括4个基本的元素:编码、选择、交叉和变异,其数学模型可以表述为
GA=(C,F,P,N,S,E,M,T)
(1)
式中:C为个体基因编码方法;F为个体适应度函数值;P为初始化的种群;N为种群的大小;S为选择算子;E为交叉算子;M为变异算子;T为GA终止的条件。
基本GA的一般流程如下:
步骤1初始化种群P,生成N个问题的初始解集,对种群个体进行二进制编码,形成种群基因。
步骤2计算个体适应度F,如果满足优化准则T,则跳到步骤6。
步骤3将个体适应度转换为被选中的概率,按照轮盘赌或者其它选择策略S选择个体,使得适应度越高的个体被选中概率越高,适应度较差的个体将被淘汰,种群往更优位置进化。
步骤4对步骤3被选中个体,按照一定概率进行基因编码交叉E,模拟生物杂交,生成新的个体,完成种群个体之间的信息共享,使GA种群往最优位置进化。
步骤5对步骤4交叉后得到的个体按照一定概率进行基因变异M,模拟生物进化过程的变异,产生新的个体,获得新的种群并回到步骤2,该步骤保证GA在后期仍然具备较强的跳出局部最优的能力。
步骤6终止运算。
从上述步骤可以看出,GA通过交叉和变异的方式可以使个体跳出局部最优,其全局搜索能力较强。但信息是在小范围共享的,在横向上通过一对一基因编码交叉共享信息,在纵向上通过优胜劣汰对比保留最优个体比,其搜索效率低,而且后期变异操纵使种群仍然活跃,导致算法收敛速度较慢。
PSO源于对鸟群捕食行为的研究[19]。优化问题的每个可能解都是PSO搜索空间中一个粒子,每个粒子都有两个属性:D维矢量位置xi(k)和D维矢量速度vi(k)。通过适用度函数F可以对每个粒子优劣进行衡量,得到单个粒子寻优路径中最优位置Li(k)和种群寻优路径中最优的位置G(k),分别作为粒子本身和种群的飞行经验,并据此调整飞行速度方向和大小,获取新的位置,从而不断靠近全局最优解。
粒子速度和位置更新关系为
(2)
式中:w为惯性权重;C1和C2为学习因子;r1和r2为0到1之间均匀分布的随机数;i为粒子序号,k为迭代步数。式(2)是PSO的核心,表明了PSO寻优的路径。
PSO数学模型可以表述为
PSO=(F,N,C1,C2,w,D)
(3)
式中:N为粒子总数。
基本PSO的一般流程如下:
步骤1初始化粒子群位置和速度,生成问题的初始解集。
步骤2计算个体适应度F,如果满足优化准则,则跳到步骤5。
步骤3根据个体适应度确定当前个体优化进程和群体优化进程中的最优位置Li(k)和G(k),该步骤使PSO在寻优过程中每个个体的信息全局共享。
步骤4按照式(3)更新粒子位置和速度,生成新的粒子群,并返回步骤2,该步骤是PSO的核心,式(3)中(Li(k)-xi(k))和(G(k)-xi(k))使每个粒子在纵向上根据自身飞行经验调整自身飞行方向,同时在横向上根据群体飞行经验来向着群体最优值移动。
步骤5终止运算。
与GA不同,PSO在寻优过程中每个个体的信息是全局共享的,使得粒子群优化算法得以快速收敛。然而在算法后期(Li(k)-xi(k))和(G(k)-xi(k))以及速度vi(k))都比较小,粒子较难跳出局部极小,导致PSO易早熟收敛到局部最优。
1.2 混合遗传粒子群优化算法
针对PSO和GA各自的特点,本文提出了混合遗传和粒子群优化算法(Hybrid Genetic Algorithm and Particle Swarm Optimization,HGAPSO),主要改进以下两点:
1) 以PSO为主体,保留算法快速收敛能力;在对粒子位置更新过程中引入GA,按照所设定的比例对部分粒子进行交叉变异操作,使粒子跳出局部最优,避免早熟。
2) 针对初始种群位置可能影响搜索效果问题,采用Kent映射[20]的方法对种群位置初始化方法进行了改进,使初始种群位置在搜索空间中尽量均匀分布,以进一步提高搜索效率和全局优化能力。如图1所示,图1(b)所示初始种群位置在整个搜索空间内分布更加均匀,而图1(a)中初始种群集中在空间某个位置,相比于图1(b)其可能无法搜索到全局最优位置。
图1 初始种群分布影响示意图
Fig.1 Influence of initial population distribution diagram
HGAPSO流程具体如下:
步骤1确定粒子种群大小N和问题维度D及可行解的上下边界,粒子速度采用常用的随机方法初始化。粒子位置根据Kent映射初始化如下:
(4)
xi,j(0)=xmin(j)+ri,j(xmax(j)-xmin(j))
(5)
式中:xi和ri维数与问题维数D相同;xmin为最小边界;xmax为最大边界;ri,j由Kent映射式(4)计算可得,其值在0~1之间均匀分布;i=1,2,…,N为粒子编号;j=1,2,…,D为维数。
步骤2根据适应度函数,评价每个粒子的适应度,确定个体最优Li(k)和群体最优G(k)(定义与粒子群算法相同),判断是否满足优化准则,满足则跳到步骤5,不满足继续步骤3。
步骤3根据PSO的式(2)更新位置和速度,使粒子群不断向着最优化位置进化。该步骤保留了PSO全局共享信息的机制,使HGAPSO具备较高的搜索效率。
步骤4引入GA的杂交和变异概念,使HGAPSO在运算后期仍具备跳出局部最优的能力,而不会早熟。具体地,以一定的概率pc选取指定比例pr的粒子放入杂交池中,作为父代粒子,两两杂交产生子代粒子,再以一定的概率pm对子代粒子位置进行变异,未交叉变异的粒子保留原位置,从而产生新一代粒子群,返回步骤2。
交叉公式为
xchild(k)=prandxparent1(k)+(1-prand)xparent2(k)
(6)
变异公式为
xnewchild(k)=xchild(k)+prand[Δ(xmin-xchild(k))+
(1-Δ)(xmax-xchild(k))]
(7)
式中:xchild为交叉子代位置;xparent为父代位置;xnewchild为变异子代的位置;prand为0~1的随机数;Δ以一定的概率p取1,以1-p的概率取0。
步骤5终止运算。
根据HGAPSO流程,其数学模型可以表达为
HGAPSO=
(F,N,C1,C2,w,M,D,pc,pm,pr,xmin,xmax)
(8)
2 气动参数模型
对于小型无人机,忽略其弹性运动,取刚体6自由度动力学微分方程组作为主控方程,并忽略动力系统的惯性力矩。针对低速小型UAV的正常飞行范围内气动辨识,主控方程中升力系数CL、阻力系数CD、侧力系数CQ、滚转力矩系数Cl、俯仰力矩系数Cm、偏航力矩系数Cn的气动数学模型分别表示为
(9)

气动辨识中所用的观测方程为
(10)
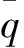
根据观测量Ζ和动力学数值积分结果Y,设计适应度函数为
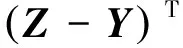
(11)
式中:Q为权重矩阵。利用优化算法,对气动模型中待辨识的参数进行优化,使适应度函数值最小,则完成气动参数的辨识。
3 基于仿真数据的HGAPSO气动参数辨识
下面基于HGAPSO进行气动参数辨识,并从辨识准度及辨识的成功率的角度,将HGAPSO与PSO和GA进行对比,然后用蒙特卡罗仿真测试随机噪声的影响。为此,取气动参数已知的某小型UAV,通过数值仿真给出其动力学特性参数,对其纵向气动参数进行辨识。
3.1 仿真试验设计
所用仿真UAV为某平直翼双尾撑布局的低速UAV,仿真初始条件为定直平飞状态,配平参数:V0=35 m/s,α0=5.88°,h0=200 m,δe0=-1.7°,T0=220.87 N。
对于纵向气动参数辨识,需要激发UAV纵向短周期和长周期运动模态,为此设计了幅值为11.46°,阶跃时间间隔为0.3 s的 “3211”周期信号[10]和时长为3 s的长脉冲信号组合作为6自由度模型的仿真输入信号,如图2所示,并预留出大约半个长周期振荡时间以得到更全面的UAV长周期模态特性。图3为6自由度模型输出的速度、迎角、俯仰角速率和俯仰角的响应曲线,从图中可以看出采用“3211”信号和长脉冲信号组合成功激励了明显的短周期和长周期运动模态。
图2 升降舵输入激励信号
Fig.2 Excitation input signal of elevator defection
图3 纵向响应曲线
Fig.3 Longitudinal response curves
3.2 3种算法的气动辨识结果
分别采用GA、PSO和HGAPSO 3种优化算法进行气动参数辨识。仿真试验按照最大迭代步数500、1 000、1 500和2 000分成4组,每组试验各进行50次辨识测试,作为初步分析,试验暂不加入观察噪声,而噪声影响在3.3节讨论。为了尽量客观对比评价3种算法,其参数设置均保持一致,采用相同的适应度函数、种群大小和上下界,GA和HGASPO算法的交叉和变异概率相同,PSO和HGAPSO粒子权重系数也相同。具体HGAPSO参数设置如下:
HGAPSO=(F,40,2,2,0.7,M,10,0.8,
0.04,0.3,xmin,xmax)
(12)
式中:
xmax=[0.2 1.5 1.4 7.8 16 1.2 1.2
0.9 -38 0.2];
xmin=[0 -0.1 -0.1 3 7 -0.3
-0.4 -4 -53 -2]。
图4显示了3种优化算法在500、1 000、1 500、2 000迭代步数下辨识成功率(辨识数值经验表明,可取适应度函数值小于300作为成功的判断标准)。结果表明在相同的迭代步数下,GA成功率较低,随着迭代步数的增加成功率缓慢增加,搜索效率较低;PSO成功率较高,搜索效率明显提高,随着迭代步数增加到一定值后成功率趋于稳定;结合了GA和PSO特点的HGAPSO,其成功率相较于GA和PSO基本算法提高很多。
表1对3种优化算法成功辨识部分的参数和代价函数的平均值进行了对比。从辨识参数真值和辨识结果来看,3种算法均有出色的寻优能力,但从适应度函数来看GA和HGAPSO显示了更好的全局优化能力,PSO则全局优化能力较弱。再分析原因,主要是因为GA采用轮盘赌和交叉变异的操作,使得群体有一定的概率往偏离最优位置方向发展,变异操作使得后期种群仍然活跃,收敛能力弱,在一定迭代步骤下其成功率下降明显,同时也正因为交叉变异使得种群可以跳出局部最优,而具有较强的全局优化能力;PSO原理简单,其全局共享信息的机制使得算法效率大大提高,但是在算法后期由于种群位置较为集中,而没有跳出局部最优的机制,使得其很难跳出局部最优。HGAPSO综合了GA和PSO的优点,具有优秀的全局优化能力和辨识效率,少量未成功辨识,是因为该算法以PSO为主体,仍有一定概率进入局部最优中,但该部分的代价函数值也都很接近300。
图4 给定迭代步数的成功率
Fig.4 Success ratios for given iterative steps
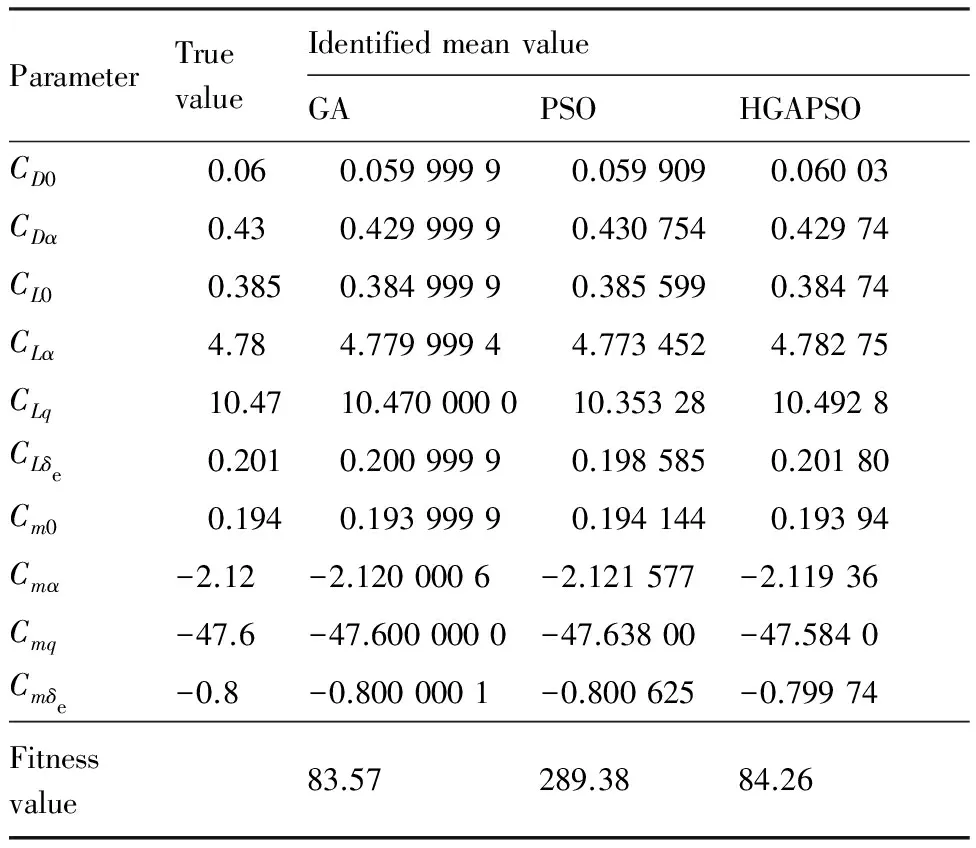
表1 辨识结果对比Table 1 Comparison of identified results
3.3 噪声影响分析
表1中之所以显示较完美的辨识效果,是因为辨识基础数据基于仿真结果,并且没有引入观测噪声,飞行参数是完全动力学协调的。为了适应在实际飞行试验中广泛存在的测量信号噪声,需进一步分析噪声对于算法辨识效果的影响。
对速度、迎角、俯仰角速率、俯仰角、法向加速度和纵向加速度观测值同时加入最大15 dB信噪比水平(相对噪声水平为17%左右)的白噪声,进行1 000次的蒙特卡罗仿真分析,并给出了气动参数辨识结果与真值相对误差的统计箱体图,如图5所示。从统计结果可以看出HGAPSO能够滤除观测信号的随机噪声影响,辨识效果好。噪声对CL0、CLα、CLq、Cm0、Cmq和Cmδe等小型UAV动态特性关键气动参数的辨识影响较小,而对CD0、CDα特别是Clδe影响较大。分析其原因,主要是因为大噪声会淹没长周期运动参数,造成相关导数可辨识性降低,从而影响阻力气动参数辨识CD0和CDα,而Clδe对于升力的贡献相对于其他升力气动导数较小,其可辨识性较差,存在噪声淹没的情况。换言之,在所加的较大噪声水平下,对操稳特性影响大的气动参数依然保持较好的辨识准度。
图5 辨识结果与真值相对误差
Fig.5 Relative errors between identified results and true values
4 基于飞行数据的HGAPSO气动参数辨识
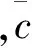
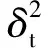
0.000 67δtV-0.003 88V2
(13)
图6 试验无人机照片
Fig.6 Photo of test UAV
式中:δt为油门大小,取值范围为0~100,代表油门从关闭到全开状态;V为空速;推力T单位为N。
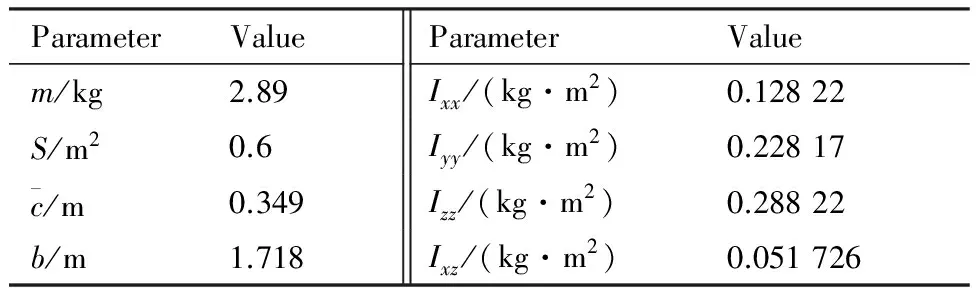
表2 试验UAV物理和几何参数Table 2 Physical and geometric parameters of test UAV
飞行参数记录系统采用开源PHIXHAWK无人机飞行控制系统[21],具有空速计、气压计、GPS模块、MEMS惯导等传感器,可采集并记录除气动角之外辨识所需的飞行数据。对于迎角和侧滑角,在风扰较小的情况下,可以通过速度投影来获取。试验当天阴天微风,近似平静大气环境,气象条件较为有利。辨识激励试验由操纵手以第3人称视角手动操纵完成。试验UAV初始平飞高度在60 m左右,速度在20 m/s左右。考虑纵向短周期运动模态基本包含了全部纵向气动参数,且噪声对长周期运动参数记录值影响较大,纵向辨识激励试验,仅对升降舵进行“3211”周期信号操纵,并留出一定时间使试验UAV纵向运动模态充分激发,油门保持不变,如图7所示。图7中:δe为升降舵偏角;δT为油门大小。横航向辨识试验,由于滚转模态收敛较快,因此先对副翼进行倍脉冲操纵激励滚转模态,然后对方向舵进行倍脉冲操纵激励荷兰滚模态,如图8所示。图8中:δa为副翼偏角;δr为方向舵偏角。
图7 纵向输入激励信号
Fig.7 Longitudinal excitation input signal
图8 横侧向输入激励信号
Fig.8 Lateral excitation input signal
辨识采用40个粒子,迭代1 000步,具体参数设置为
HGAPSO=(F,40,2,2,0.7,1 000,33,0.8,
0.04,0.3,xmin,xmax)
(14)
式中:可行解的上下界一般依据风洞试验结果、CFD或工程计算结果给出,这里参考同类小型无人机气动参数辨识的结果[4,22],利用参数预估计方法[8]得到,具体为
xmax=[0.2,0.5,2,0.15,0.15,6,20,1,0.6,0.5,
-0.05,-0.1,0.5,-0.1,0.1,-0.1,
-0.01,0.2,0,0.6,0.01,0,0,0.2,0,0.2,
0.01,0.1,0,0.5,0.1,0]
xmin=[0,0.05,0.2,-0.1,-0.1,0,0,-0.1,
0,-0.5,-0.8,-10,-0.5,-1,0,-1,
-0.2,0,-0.2,0,-0.01,-0.2,-0.5,0,
-0.2,0,-0.01,0,-0.2,0,-0.1,-0.5]
试验UAV气动参数辨识结果如表3、表4所示。通过辨识得到模型输出和飞行试验数据的对比如图9、图10所示。纵向试验为310~315 s,横侧向试验为两段数据,451~453 s为副翼激励试验段,513~517 s为方向舵激励试验段。

表3 纵向气动参数辨识结果Table 3 Identified values of longitudinal parameters
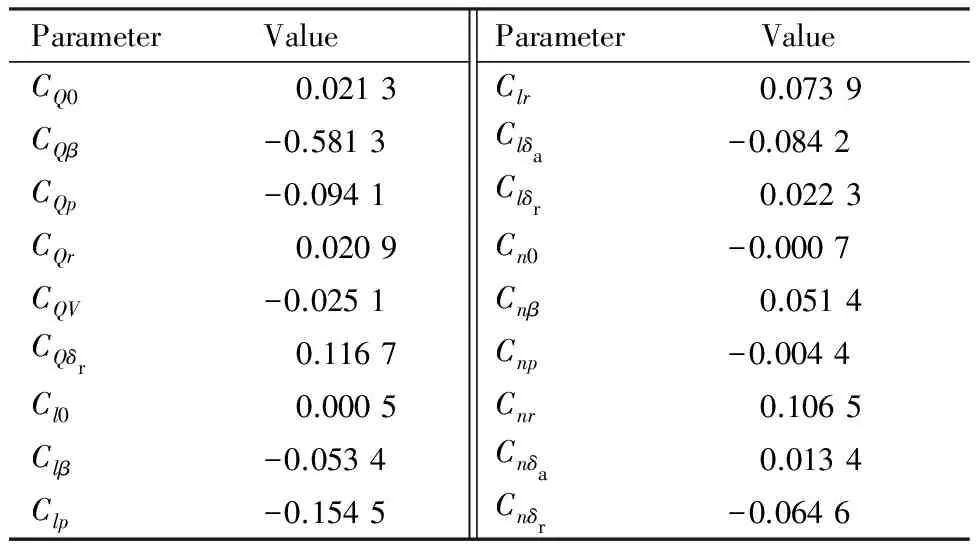
表4 横侧向气动参数辨识结果Table 4 Identified values of lateral parameters
图9 纵向飞行数据时序图
Fig.9 Time histories of longitudinal flight data
图10 横侧向飞行数据时序图
Fig.10 Time histories of lateral flight data
可以看出,辨识模型预测输出的数据和原始飞行数据吻合很好,表明了HGAPSO有效性,同时也表明该算法具有较强的高维空间优化能力,适于处理实际工程问题。
5 结 论
本文融合了遗传算法(GA)和粒子群算法(PSO)的优点,提出了新型的混合遗传粒子群优化算法(HGAPSO)用于气动参数辨识,辨识精度好,辨识成功率高,对随机观测噪声不敏感。
1) HGAPSO以PSO为主体,在进行粒子位置更新时引入GA的交叉变异操作,同时采用Kent映射改进了种群初始化的方法,能够兼备PSO高的搜索效率和GA的全局优化能力。
2) HGAPSO可以解决高维度空间的气动参数辨识问题,精准辨识出气动参数,在存在随机观测噪声的情况下仍然具备较高的辨识精度。
3) 基于飞行试验的辨识结果表明,本文建立的气动参数模型结构能够反映小型UAV正常包线飞行中的气动特性,可以确保获得良好的气动辨识结果。
本文的气动参数辨识方法,可以推广到其他类型飞行器,并结合其气动模型结构特征进行参数辨识。
[1] MELANSON M, CHANG M, BAKER W II. Wind tunnel testing’s future: A vision of the next generation of wind tunnel test requirements and facilities[C]//48th AIAA Aerospace Sciences Meeting. Reston: AIAA, 2010.
[2] SIMSEK O, TEKINALP O. System identification and handling quality analysis of a UAV from flight test data[C]//AIAA Atmospheric Flight Mechanics Conference. Reston: AIAA, 2015.
[3] 丁娣, 钱炜祺, 汪清. 飞机操稳特性大导数辨识及随机噪声影响分析[J]. 航空学报, 2015, 36(7): 2177-2185.
DING D, QIAN W Q, WANG Q. Identification of aircraft stability and control characteristics derivatives and analysis of random noises[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2177-2185 (in Chinese).
[4] JIANG T Y, LI J, HUANG K. Longitudinal parameter identification of a small unmanned aerial vehicle based on modified particle swarm optimization[J]. Chinese Journal of Aeronautics, 2015, 28(3): 865-873.
[5] CHASE A, ROBERT A. Flight testing small UAVs for aerodynamic parameter estimation[C]//AIAA Atmospheric Flight Mechanics Conference. Reston: AIAA, 2014.
[6] 吴伟, 陈仁良. 直升机悬停状态全耦合飞行动力学模型辨识方法[J]. 航空学报, 2011, 32(2): 202-211.
WU W, CHEN R L. Identification method for helicopter fully coupled flight dynamics model in hover condition[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(2): 202-211 (in Chinese).
[7] 雷宇. 基于STA34的无人机模型辨识与自主飞行控制律设计[D]. 北京: 北京航空航天大学, 2013: 26-56.
LEI Y. Model identification and autonomous flight control law design based on STA34 autopilot[D]. Beijing: Beihang University, 2013: 26-56 (in Chinese).
[8] 蔡金狮, 汪清, 王文正. 飞行器系统辨识学[M]. 北京: 国防工业出版社, 2003: 125-216.
CAI J S, WANG Q, WANG W Z. Flight vehicle system identification [M]. Beijing: National Defence Industry Press, 2003: 125-216 (in Chinese).
[9] KLEIN V, EUGENE A. Aircraft system identification-theory and practice[M]. Reston: AIAA, 2006: 27-221.
[10] RAVINDRA V. Flight vehicle system identification: A time domain methodology[M]. Reston: AIAA, 2006: 59-261.
[11] BURCHETT A. Aerodynamic parameter identification for symmetric projectiles: Comparing gradient based and evolutionary algorithms[C]//AIAA Atmospheric Flight Mechanics Conference. Reston: AIAA, 2011.
[12] 钱炜祺, 汪清, 王文正. 遗传算法在气动力参数辨识中的应用[J]. 空气动力学报, 2003, 21(2): 196-201.
QIAN W Q, WANG Q, WANG W Z. Aerodynamic parameter identification using GA[J]. Journal of Aerodynamic, 2003, 21(2): 196-201 (in Chinese).
[13] 张天姣, 汪清, 何开锋. 粒子群算法在气动力参数辨识中的应用[J]. 空气动力学报, 2010, 28(6): 633-635.
ZHANG T J, WANG Q, HE K F. Aerodynamic parameter identification using PSO[J]. Journal of Aerodynamic, 2010, 28(6): 633-635 (in Chinese).
[14] 刘国平, 徐钦龙. 粒子群算法及其与遗传算法的比较[J]. 中南工业大学学报, 2003, 34(2): 328-330.
LIU G P, XU Q L. Comparing PSO and GA[J]. Journal of Central South University of Technology, 2003, 34(2): 328-330 (in Chinese).
[15] IBRAHIM A S N, SELAMAT. A query optimization in relevance feedback using hybrid GA-PSO for effective web information retrieval[C]//2009 Third Asia International Conference on Modelling & Simulation. Piscataway, NJ: IEEE Press, 2009.
[16] HUANG H. Global path planning for autonomous robot navigation using hybrid metaheuristic GA-PSO algorithm[C]//2011 Proceedings of SICE Annual Conference (SICE). Piscataway, NJ: IEEE Press, 2011: 1338-1343.
[17] SHAMA J, SINGHAL R S. Comparative research on genetic algorithm, particle swarm optimization and hybrid GA-PSO[C]//Computing for Sustainable Global Development. 2015: 110-114.
[18] HOLLAND J H. Genetic algorithms[J]. Scientific American, 1992, 267(1): 66-72.
[19] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Piscataway, NJ: IEEE Press, 1995: 1942-1948.
[20] 杨迪雄. 非线性函数的混沌优化方法比较研究[J]. 计算力学学报, 2004, 21(3): 257-262.
YANG D X. Comparative study on chaos optimization algorithm for nonlinear function[J]. Chinese Journal of Computational, 2004, 21(3): 257-262 (in Chinese).
[21] PIXHAWK. Pixhawk autopilot introduction[EB/OL]. [2016-04-15]. http://www.pixhawk.com/modules/pixhawk.
[22] GÖTTLICHER C. System identification of an unmanned aerial vehicle using maximum likelihood methods[D]. München: Technische Universität München, 2013: 92-108.
HGAPSO:Anewaerodynamicparametersidentificationalgorithmforsmallunmannedaerialvehicles
SHAOGan1,ZHANGShuguang1,2,3,*,TANGPeng2,3,4
1.SchoolofTransportationsScienceandEngineering,BeihangUniversity,Beijing100083,China2.BeijingKeyLaboratoryforAircraft/EngineIntegratedSystemSafety,Beijing100083,China3.CollaborativeInnovationCenterforAdvancedAero-Engine,Beijing100083,China4.SchoolofEnergyandPowerEngineering,BeihangUniversity,Beijing100083,China
Inthedevelopmentofsmallunmannedaerialvehicles(UAVs),aerodynamicparameteridentificationisneededforstabilityandcontrolanalysisandflightcontrollawassessment.Animprovedhybridgeneticandparticleswarmoptimizationalgorithm(HGAPSO)isproposedforaerodynamicparameteridentification.Inthisalgorithm,theparticleswarmoptimizationalgorithm(PSO)isusedasthemainbody,andthecross-overandmutationoperationofgeneticalgorithm(GA)isincludedintotheoptimizationofparticlepathtoenhancetheabilitytojumpoutofthelocaloptimalpath.Kentmappingisalsousedtoimprovetheinitialdistributionoftheparticlepopulation,andtomakethedistributionmoreuniformandthentheoptimizationmoreglobal.Basedonthesimulationresults,theHGAPSO,PSOandGAalgorithmsarecomparedintermsofaccuracyofidentifiedaerodynamicparametersandsuccessrateofidentification.MonteCarlosimulationsarefurtherconductedtoevaluatetheeffectofrandomnoisesinthemeasuredsignals.TheresultsshowthatHGAPSOcanprovidebothhighefficiencyandglobalizationinoptimization,andhasgoodresistanceagainstmeasurednoises.FlighttestingdataacquiredfromasmallUAVareusedtocomprehensivelyevaluatetheHGAPSOalgorithm,andtheHGAPSOshowssatisfactoryabilitytoidentifyaerodynamicparametersbasedontheflightdata.
smallunmannedaerialvehicle;aerodynamicparameter;parameteridentification;hybridgeneticandparticleswarmoptimizationalgorithm(HGAPSO);searchingefficiency;globaloptimization
2016-04-25;Revised2016-06-02;Accepted2016-06-15;Publishedonline2016-06-271534
URL:www.cnki.net/kcms/detail/11.1929.V.20160627.1534.010.html
NationalHigh-techResearchandDevelopmentProgramofChina(2014AA2157)
2016-04-25;退修日期2016-06-02;录用日期2016-06-15; < class="emphasis_bold">网络出版时间
时间:2016-06-271534
www.cnki.net/kcms/detail/11.1929.V.20160627.1534.010.html
国家“863”计划 (2014AA2157)
*
.E-mailgnahz@buaa.edu.cn
邵干, 张曙光, 唐鹏. 小型无人机气动参数辨识的新型HGAPSO算法J. 航空学报,2017,38(4):120365.SHAOG,ZHANGSG,TANGP.HGAPSOAnewaerodynamicparametersidentificationalgorithmforsmallunmannedaerialvehiclesJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):120365.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0196
V212.11
A
1000-6893(2017)04-120365-11
(责任编辑: 鲍亚平, 蔡斐)
*Correspondingauthor.E-mailgnahz@buaa.edu.cn

