一种改进的果蝇优化算法及其在气动优化设计中的应用
田旭, 李杰
西北工业大学 航空学院, 西安 710072
一种改进的果蝇优化算法及其在气动优化设计中的应用
田旭, 李杰*
西北工业大学 航空学院, 西安 710072
果蝇优化算法(FOA)是一种新的群体智能优化算法,具有良好的全局收敛特性。为进一步提高FOA的寻优性能,将其引入到气动优化设计中,发展形成了改进的果蝇优化算法(IFOA)。IFOA通过引入惯性权重函数动态调整搜索步长,有效实现了算法全局搜索和局部搜索之间的动态平衡,提高了算法整体搜索效率和寻优精度;对于多维优化问题,IFOA每次搜索仅随机扰动其中一个决策变量,并在每个迭代步内将所有优秀果蝇个体(可行解)结合产生一个全新的果蝇个体进行一次搜索,大大加快了算法的收敛速度。函数测试结果表明,IFOA显著提高了FOA的寻优性能。将IFOA 应用到气动优化设计中,翼型反设计和单/多目标优化设计的算例表明,IFOA是一种简单高效的优化方法,可广泛应用于气动优化设计。
果蝇优化算法; 味道浓度; 搜索步长; 翼型; 气动优化设计
飞行器气动外形优化设计是现代航空工程实践中的关键问题之一。传统的气动优化设计方法不但严重依赖于设计人员的设计经验,而且需要消耗大量的人力、物力和财力。近年来,随着最优化理论和CFD技术的快速发展,采用最优化方法进行飞行器气动优化设计成为主要手段之一。最优化方法分为局部最优化方法和全局最优化方法,局部最优化方法诸如最速下降法、共轭梯度法等优化效率较高,但由于算法的局部搜索特性,优化过程容易陷入局部最优而得不到全局最优解;全局最优理论与算法远没有局部最优算法成熟,但其良好的全局寻优特性弥补了局部最优算法在解决多峰问题中的不足,受到人们的广泛关注。以遗传算法为代表的启发式智能优化算法采用适当的状态转移规则和概率性状态接受规则,能够避免过早地陷入局部最优解,具有良好的全局收敛特性。典型的启发式智能优化算法主要有:遗传算法、蚁群算法、粒子群算法、模拟退火算法、禁忌搜索算法和差分进化算法等,已经逐渐应用于气动外形的优化设计中,取得了显著的效果[1-4]。
果蝇优化算法(Fruit fly Optimization Algorithm,FOA)[5-6]是一种基于果蝇觅食行为的启发式智能优化算法,由潘文超2011年提出,用于金融预警模型的研究[7]。FOA具有很好的群体智能性,和其他智能优化算法相比,FOA具有算法简单、程序代码易于实现、调节参数较少、计算量小、全局寻优能力强且寻优精度高等优点[8],现已成功应用于求解数学函数极值、求解投资组合模型、广义回归神经网络参数优化与支持向量机参数优化等诸多科学和工程领域[9-14]。因此,发展改进FOA并将其引入气动优化设计领域非常有必要。
本文在搜索步长、寻优策略2方面对原始的FOA进行改进,并结合参考文献,提出了改进的果蝇优化算法(Improved Fruit fly Optimization Algorithm,IFOA),使得改进后的算法寻优性能大大提高。将IFOA成功应用于翼型反设计和单/多目标优化设计中,取得了良好的结果。
1 果蝇优化算法
FOA是将果蝇寻找食物的过程进行仿真模拟,从而形成具有全局搜索能力的优化算法。果蝇具有敏锐的嗅觉和视觉系统,对食物的味道具有超强的感知能力,食物的味道越浓,果蝇的感知能力越强。果蝇个体利用其良好的嗅觉器官能迅速在空气中捕捉到食物的味道,然后飞近食物,其他同伴利用敏锐的视觉系统迅速聚集到食物味道最浓的果蝇位置,果蝇搜索食物的过程就是不断从味道浓度小的地方转移到味道浓度大的地方,直到找到食物源,整个搜寻食物的过程如图1所示。图中,Fly group代表果蝇群体聚集位置,Fly则表示果蝇个体的搜寻方向,Dist为果蝇个体与原点之间的距离,S为距离的倒数,表示果蝇个体的味道浓度判定值,Smell为其对应的味道浓度值,是味道浓度判定值的函数。
FOA引入了味道浓度判定值和味道浓度判定函数,其功能类似于其他演化算法中的适应度函数。在寻优过程中,果蝇群体根据个体的位置和味道浓度(由味道浓度判定值和味道浓度判定函数决定)来改变自己的位置,不断接近味道浓度最大的位置,也就是最优解所在的位置。FOA的流程图如图2所示。算法具体步骤详见文献[5]。
图1 果蝇群体搜索食物过程
Fig.1 Food finding process of fruit fly swarm
FOA利用果蝇群体的协作机制和信息共享机制搜寻种群最优解,全局寻优能力强,收敛精度高;FOA的优化方程是一阶微分方程,且算法采用实数编码,因而算法较为简单,程序代码易于实现,计算量较小;FOA的调节参数只有4个,显然比其他智能优化算法要少得多,大大减小了因参数取值不当而对算法性能产生影响的机会。尽管FOA已经在工程应用领域表现出很大的研究价值,但也存在一些缺陷需要改进。
原始的FOA采用固定搜索步长,在寻优过程中很难同时兼顾全局搜索能力和局部搜索能力,影响了算法的收敛速度和收敛精度。因此,如何改进FOA使之具有良好的全局/局部搜索平衡能力是一个值得探讨的问题。
图2 果蝇优化算法流程图
Fig.2 Flow chart of fruit fly optimization algorithm
FOA的另一个局限性关于味道浓度判定值。在潘文超的著作[5]中,味道浓度判定值Si定义为果蝇个体与原点之间距离的倒数,如此定义的Si存在3个缺陷:① 由于Si>0,故FOA不能求解定义域包含负数的优化问题,当然也不能直接应用于气动优化设计中;②Si容易导致算法早熟,陷入局部最优解;③Si不服从均匀分布,减弱了算法的全局搜索能力。对此,已有部分文献给出了一些解决方案[15-16]。
2 改进的果蝇优化算法
现有文献中对于FOA的改进主要从两方面进行研究:一是算法自身的完善和改进[17-18],二是将FOA与其他智能算法相结合[19-20]。本文主要针对算法自身进行完善和改进,使其能够更好地应用于气动优化设计。
2.1 算法描述
在FOA以及各类改进算法中,搜索步长一般分为固定搜索步长和自适应搜索步长。自适应搜索步长通过引入果蝇因子(权重系数)修改步长公式,根据果蝇个体与最优解之间的距离动态地调整搜索步长,从而有效地实现了算法全局搜索能力和局部搜索能力之间的动态平衡。本文发展的IFOA通过引入惯性权重函数w[21]动态调整算法的搜索步长,将其分为3段:首先保持较大的搜索步长,使算法在较大区域内进行搜索,保证算法的全局搜索能力;接着由较大搜索步长逐渐过渡到较小搜索步长;最后保持较小的搜索步长直到算法运行结束,使算法在较小的区域内进行精细化搜索,保证算法的局部搜索能力。惯性权重函数w和果蝇个体随机搜索的表达式为
(1)
图3 函数w的曲线
Fig.3 Curves of function w
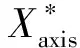
从函数w的曲线图可以看出,k2固定,k1越大则算法在较小搜索步长下搜索时间越长,局部搜索能力变强;反之,当k1固定,k2越大则算法在较大搜索步长下搜索时间越长,全局搜索能力变强。图3中的函数曲线为k1和k2的取值提供了基本的参考,可在此基础上根据实际问题的需求和特点做相应的调整。
对于多维优化问题(比如n维),每个迭代步内果蝇群体聚集的位置(当前最优变量)是一个n维向量,赋予果蝇个体随机方向和距离也就是对该向量进行随机扰动,形成新的搜索方向。为进一步提高算法的搜索效率,IFOA在每次搜索时只针对该向量的其中一个分量进行扰动(每次仅随机改动一个决策变量),随后果蝇个体沿该方向搜寻食物[22];若该果蝇个体的搜索方向更接近食物源,则记录该方向,反之则舍弃;在每一个迭代步内,用这些记录的分量更新原果蝇群体聚集位置对应的分量,组成一个新的搜索方向,也就是产生一个新的果蝇个体,并沿该方向进行一次搜索;最后比较该新果蝇个体与其余果蝇个体所在位置的味道浓度与上一代最佳味道浓度的大小,记录并转入下一步骤。
另外,若想将FOA引入到气动优化设计中,则必须解决算法不能处理负数定义域优化问题的缺陷,为此,IFOA采用文献[16]中提到的方法,将果蝇个体直接作为味道浓度判定值代入味道浓度判定函数进行计算。
基于以上分析, IFOA相比于FOA存在3点不同:① 采用自适应搜索步长,使得算法具有良好的全局/局部搜索平衡能力,提高了算法的搜索效率和寻优精度;② 对于多维优化问题,每次搜索只随机改动其中一个决策变量,并且在每一个迭代步内将所有优秀果蝇个体结合产生一个新果蝇个体进行一次搜索,加快了算法的收敛速度;③ 将果蝇个体直接作为味道浓度判定值代入味道浓度判定函数进行计算,既保证算法在整个定义域内均匀搜索,又解决了FOA不能处理负数定义域优化问题的缺陷。
2.2 算法步骤
多维(n维)优化问题的表达式为
minf(x1,x2,…,xn)
s.t.xj∈[LBj,UBj]j=1,2,…,n
(2)
式中:LBj和UBj分别为自变量xj的左右边界。
求解该问题的IFOA具体步骤如下:
步骤1参数初始化。给定果蝇种群规模sizepop,最大迭代次数maxgen,惯性权重函数的参数k1和k2。
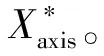
(3)
步骤3随机搜索。赋予果蝇个体利用嗅觉搜寻食物的随机方向和距离。设ci=d为[1,n]之间的一个随机整数,Xi=(xi,1,xi,2,…,xi,n)是第i个果蝇个体对应的决策变量,则
(4)
式中:j=1,2,…,n;w和step的表达式为
(5)
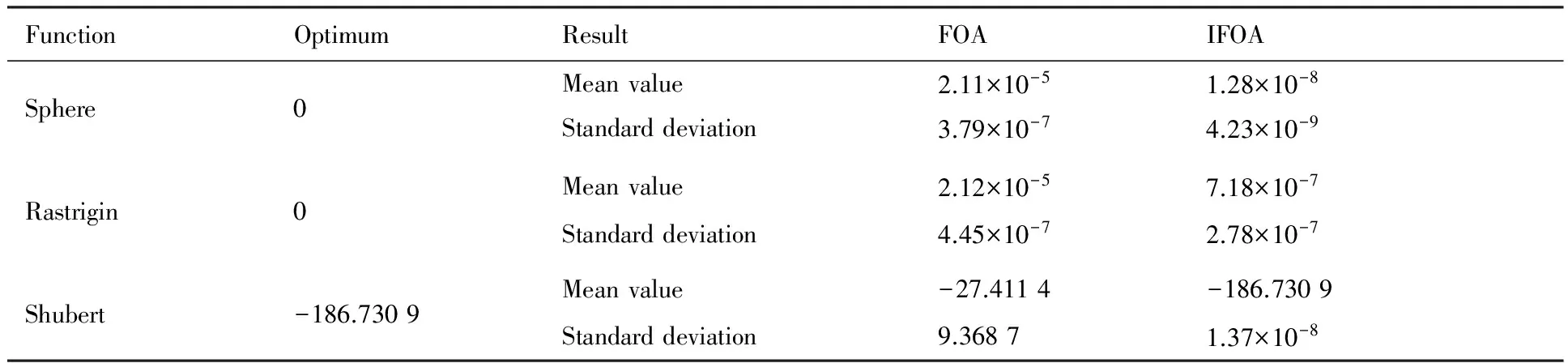
若xi,j>UBj或xi,j 步骤4将味道浓度判定值Xi代入味道浓度判定函数,计算果蝇个体位置所对应的味道浓度值Smelli,并记录所有味道浓度优于上代最佳味道浓度的果蝇个体所对应的扰动变量。 Smelli=Function(Xi) (6) 步骤5根据味道浓度值,找出当前果蝇群体中味道浓度最优的果蝇个体(最优个体)。 [bestSmell*bestIndex*]=min(Smelli) (7) 式(7)是MATLAB求最小值的代码形式,右边表示求最小值,左边表示记录最大值bestSmell*以及所对应的序号bestIndex*。 (8) smellNew=Function(Xnew) (9) smellBest*=bestSmell* (10) smellBest*=smellNew (11) 步骤9果蝇群体利用敏锐的视觉向最佳味道浓度所在位置聚集,进入迭代寻优直到满足终止条件,结束算法。 在IFOA以及FOA中,参数的选取对算法的寻优性能有重要的影响。一般而言,迭代次数越大,寻优结果越精确,但耗时更长;增加果蝇种群规模可以在一定程度上提高算法的收敛速度,但同时计算量会相应增加,且收敛速度的提高也有限,文献[14]中提到,对于大部分问题而言,20~50个果蝇个体就可以取得不错的效果,但对于一些大规模复杂问题,果蝇个体的数量有时需要取到100甚至更多。 2.3 函数测试 为了测试并分析算法的寻优性能,选用如下3个典型的测试函数对IFOA进行函数测试。 1) Sphere函数 (12) 式中:-10≤xi≤10,i=1,2,…,n。 Sphere函数是一个较为简单的非线性对称单峰函数,在xi=0(i=1,2,…,n)处取得全局最小值0,这里取n=30。 2) Rastrigin函数 (13) 式中:-5.12≤xi≤5.12,i=1,2,…,n。 Rastrigin函数是一个多峰函数,具有大量按正弦拐点排列的局部最优点,优化算法在求解过程中很容易陷入某一个局部最优点。该函数在xi=0(i=1,2,…,n)处达到全局最小值,最小值为0,这里取n=30。 3) Shubert函数 (14) 式中:-10≤x1,x2≤10。 Shubert函数是一个多峰函数,具有大量的局部最小值点,全局最优值为-186.730 9。 所有测试函数中,果蝇种群规模取为50,最大迭代次数为500,FOA中果蝇群体的位置区间和随机搜索区间均取为[-10,10],IFOA中惯性权重函数的参数取为:k1=10,k2=3。对每个测试函数均独立进行100次优化观察其结果。如果最终的寻优结果在最优值的2.2×10-5范围内,则称本次寻优成功且将迭代的次数保留下来。定义两个衡量指标分别为成功率(PS)和平均有效迭代次数( AVIN )[16]: (15) (16) 式中:m为100次实验中成功的次数;ni为第i次成功实验的迭代次数。 表1列出了3个测试函数分别采用FOA和IFOA进行100次优化所得结果的均值和标准差,表2是100次优化的成功率和平均有效迭代次数。 表1 函数测试的均值和标准差Table 1 Mean value and standard deviation of function test 表2 函数测试的成功率和平均有效迭代次数Table 2 PS and AVIN of function test 从表1和表2的测试结果可以看出:FOA和IFOA均具有较强的全局寻优能力,但FOA在求解一些特定的优化问题(如Shubert函数等)时表现较差。一方面,在调用目标函数次数相同的条件下,无论平均值还是标准差,IFOA的优化结果均要优于FOA,表明IFOA相比于FOA具有更高的收敛精度;另一方面,在相同的收敛精度条件下,IFOA的平均有效迭代次数小于FOA,表明IFOA的收敛速度更快。因此,本文对FOA的改进是有效的,与FOA相比,IFOA在求解优化问题时具有更快的收敛速度和更高的收敛精度,且适用性更为广泛。 翼型优化设计是飞行器气动外形优化设计的重要组成部分之一,快速有效地设计出满足工程需要的翼型一直是科研工作者努力的目标。本节将IFOA引入到气动优化设计中,完成了跨声速翼型的反设计以及单/多点减阻优化设计。 3.1 翼型参数化 翼型的参数化描述对翼型的优化设计效率和优化结果有重要影响。解析函数线性叠加法简单实用,通过基准翼型和型函数的线性叠加来表示翼型函数,其上下翼面的表达式为 (17) 式中:ybasic为基准翼型坐标;ck为设计变量;M为型函数的个数;fk(x)为所选型函数。 常用的型函数有多项式型函数、Hicks-Henne型函数和Wagner型函数等。本文采用改进的Hicks-Henne型函数[23]对翼型进行参数化描述,即在原Hicks-Henne型函数[24]后缘处增加一个函数项fM(x)=αx(1-x)e-β(1-x),用以解决Hicks-Henne型函数不能改变翼型后缘夹角的缺陷,具体表达式为 (18) 本文选取16个设计变量来确定翼型,其中上下翼面各8个设计变量。 3.2 流场数值求解方法 本文的流场求解采用雷诺平均Navier-Stokes方程作为流动控制方程,湍流模型选用B-L湍流模型。对于Navier-Stokes方程的求解,空间离散选用格心格式的中心有限体积法,时间推进采用五步龙格-库塔格式,采用无限插值代数网格生成方法生成C型结构化网格。为加快收敛速度,计算中采用了当地时间步长、隐式残值光顺和多重网格等加速收敛措施。 为了验证流场数值求解方法的可靠性,选取了RAE2822跨声速翼型进行数值验证,计算状态为Ma=0.729,α=2.31°,Re=6.5×106,分别采用网格Ⅰ(257×65)、网格Ⅱ(321×85)、网格Ⅲ(369×101)这3套不同密度的网格对其进行计算。图4给出了网格密度为321×85的网格示意图,图5给出了3套网格计算压力系数Cp分布和实验结果[25]的对比。从图中可以看出,网格Ⅱ和网格Ⅲ的计算结果都能够很好地反映流动规律,考虑到计算效率和准确度问题,本文后续的算例均采用321×85的网格密度分布进行流场计算。 图4 RAE2822翼型计算网格(321×85)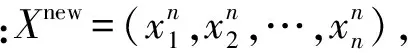
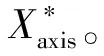

3 翼型优化设计
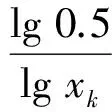
Fig.4 Computational grids around RAE2822 airfoil (321×85)
图5 不同网格密度的计算压力系数分布
Fig.5 Pressure coefficients distribution for different grid density
3.3 翼型反设计
对于给定目标压力分布的反设计问题,其目标函数的定义为
(19)
式中:CpT为给定的目标压力系数,积分区域为整个翼型表面s。以NACA0012翼型为基准翼型,在Ma=0.73,α=2.0°,Re=6.5×106状态下进行翼型反设计,目标压力系数分布取为RAE2822在该设计状态下的计算压力系数分布。
翼型反设计中取果蝇种群规模为25,最大迭代次数为50,惯性权重函数的参数分别取为:k1=10,k2=3。
图6和图7分别给出了初始翼型、目标翼型和最终设计翼型的形状以及表面压力系数分布,从图中可以看出,设计翼型与目标翼型RAE2822的几何外形以及表面压力系数分布均吻合良好,仅在局部区域有很小的误差,表明了本文建立的流场数值模拟方法和基于IFOA的气动优化设计方法的可靠性。
图6 翼型几何形状对比
Fig.6 Comparison of airfoil shapes
图7 翼型压力系数分布对比
Fig.7 Comparison of pressure coefficients distribution of airfoil
3.4 单目标优化设计
考虑超临界翼型RAE2822在Ma=0.73,α=2.79°,Re=6.5×106设计状态下对该翼型进行单点减阻优化设计。
优化目标为最小化翼型阻力系数CD,优化过程加入升力系数CL、力矩系数Cm以及翼型面积A等约束条件。优化目标和约束条件的数学描述为
minCD
(20)
式中:下标“0”指初始状态。
翼型单点减阻优化设计中取果蝇种群规模为25,最大迭代次数为50,惯性权重函数的参数分别取为:k1=10,k2=3。
图8和图9分别给出了优化前后翼型的形状以及相应的表面压力系数分布对比,表3为优化前后的几何特性以及气动特性,表中K为升阻比。
从翼型优化前后的对比结果可以看出,IFOA的减阻效果是明显的,且满足规定的约束条件。从几何形状上看,优化翼型上下表面均发生不同程度的改变,其中上表面变化较大,最大厚度位置后移,而下表面变化则较小;从表面压力系数分布上看,优化翼型的前缘吸力峰值增大,上表面压力过渡更为和缓,激波强度显著减弱;从气动力上看,优化翼型的阻力系数从初始的0.018 69减小到0.014 45,减小了22.69%,升力系数略有增加,翼型面积基本保持不变,升阻比从42.53增加到55.04,增加了29.41%,气动性能得到较大改善。综合来看,翼型上表面形状的变化对压力系数分布的影响较大,这也反映了跨声速流动的特点。
图8 单目标优化翼型几何形状对比
Fig.8 Comparison of airfoil shapes with single-objective optimization
图9 单目标优化翼型压力系数分布对比
Fig.9 Comparison of pressure coefficient distribution with single-objective optimization

表3 翼型单目标优化前后性能对比
3.5 多目标优化设计
对于多目标优化问题,通常采用加权法将多目标优化问题转化为单目标优化问题。本节考虑两点优化问题,仍以RAE2822作为基本翼型, 设计状态如下:
1)Ma=0.72,α=2.7°,Re=5.5×106。
2)Ma=0.74,α=2.2°,Re=5.5×106。
在翼型面积和升力系数不减小的约束条件下,使翼型在2个设计状态的阻力系数均减小。目标函数和约束条件的数学表达式为
minw1CD1+w2CD2
(21)
式中:CD1、CD2和CL1、CL2分别为2个设计状态的阻力、升力系数;下标init表示翼型初始气动参数;w1和w2分别为2个设计状态下的加权因子,反映了不同设计目标的权重,这里取w1=w2=0.5。多目标优化设计中取果蝇种群规模为20,最大迭代次数为30,惯性权重函数的参数分别取为:k1=10,k2=3。
表4给出了优化前后翼型的几何特性以及气动特性,在状态1,翼型的阻力系数从0.015 00减小到0.014 19,减小了5.4%,状态2的阻力系数也从0.016 87减小到0.015 10,减小了10.49%,2个设计状态下的升力系数都略有增加,升阻比分别增加了5.75%和11.97%,翼型面积也有所增加。
图10和图11分别给出了2个设计状态下的表面压力系数分布,从图中可以看出设计状态1的激波强度减弱,前缘吸力峰值有所增大,设计状态2的压力系数分布也有所改善。图12给出了优化前后的翼型形状对比。由于目标函数中加权因子取值的关系,2个设计状态下的翼型气动特性得到不同程度的改善,可以通过调整各设计状态加权因子的大小来确定对应设计状态在优化过程中所占的权重,从而改变最终的优化结果。
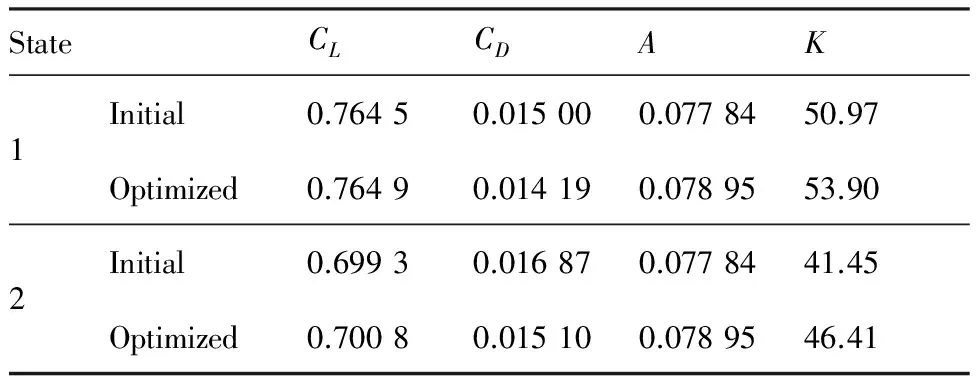
表4 翼型多目标优化前后性能对比
图10 设计状态1压力系数分布
Fig.10 Pressure coefficient distribution at design state 1
图11 设计状态2压力系数分布
Fig.11 Pressure coefficient distribution at design state 2
图12 多目标优化翼型几何形状对比
Fig.12 Comparison of airfoil shapes with multi-objectives optimization
4 结 论
1) IFOA在搜索步长、寻优策略两方面对FOA的改进,使得算法具有良好的全局/局部搜索平衡能力以及更快的收敛速度。函数测试结果表明,FOA和IFOA均具有较强的全局寻优能力,但IFOA在收敛速度和收敛精度等方面优于FOA,且适用性更为广泛。
2) 将IFOA引入到气动优化设计中,翼型反设计以及单/多目标优化设计的算例结果表明,IFOA只需调用较少次数的流场计算就可以得到较为满意的优化结果,表现出非常好的寻优性能,是一种简单高效的优化方法,能够满足气动优化设计的需求。
3) 本文给出的几个气动优化设计算例相对较为简单,对于更复杂的气动优化问题,比如全机复杂构型体的外形优化,同时兼顾起飞、巡航以及着陆状态的多目标优化等,优化算法本身并不会有本质区别,完全可以通用,只需考虑优化系统中的流场求解以及参数化等问题,也就是说,IFOA很容易推广到复杂气动优化问题。
FOA是一个较新的研究领域,目前国内外的相关文献还较少,相比遗传算法等较为成熟的智能优化算法来说,FOA的理论和应用研究还远远不够。但不可否认,随着人们对其研究的不断深入,FOA的潜能正在不断被挖掘出来,进而将其应用于解决更广泛和复杂的实际问题。
[1] RAY T, TSAI H M. Swarm algorithm for single- and multi-objective airfoil design optimization[J]. AIAA Journal, 2004, 42(2): 366-373.
[2] 李丁, 夏露. 改进的粒子群优化算法在气动设计中的应用[J]. 航空学报, 2012, 33(10): 1809-1816.
LI D, XIA L. Application of improved particle swarm optimization algorithm to aerodynamic design[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(10): 1809-1816 (in Chinese).
[3] 余刚. 基于混合遗传算法和复合形法的翼型优化设计[D]. 西安: 西北工业大学, 2007.
YU G. Optimization design of airfoil based on hybrid genetic algorithm and compound form method[D]. Xi’an: Northwestern Polytechnical University, 2007 (in Chinese).
[4] DUAN Y H, CAI J S, LI Y Z. Gappy proper orthogonal decomposition-based two-step optimization for airfoil design[J]. AIAA Journal, 2012, 50(4): 968-971.
[5] 潘文超. 果蝇最佳化演算法[M]. 台北: 沧海书局, 2011.
PAN W C. Fruit fly optimization algorithm[M]. Taipei: Tsang Hai Publishing, 2011 (in Chinese).
[6] PAN W C. A new evolutionary computation approach: Fruit fly optimization algorithm[C]//2011 Conference of Digital Technology and Innovation Management, 2011.
[7] PAN W C. A new fruit fly optimization algorithm: Taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69-74.
[8] 吴小文, 李擎. 果蝇算法和5种群智能算法的寻优性能研究[J]. 火力与指挥控制, 2013, 38(4): 17-25.
WU X W, LI Q. Research of optimizing performance of fruit fly optimization algorithm and five kinds of intelligent algorithm[J]. Fire Control & Command Control, 2013, 38(4): 17-25 (in Chinese).
[9] 张勇, 夏树发, 唐冬生. 果蝇优化算法对多峰函数求解性能的仿真研究[J]. 暨南大学学报(自然科学与医学版), 2014, 35(1): 82-87.
ZHANG Y, XIA S F, TANG D S. Simulation of multi-peak function based on the fly optimization algorithm[J]. Journal of Jinan University (Natural Science & Medicine Edition), 2014, 35(1): 82-87 (in Chinese).
[10] 单单. 止损策略对双随机安全第一投资组合模型的影响研究[D]. 重庆: 重庆大学, 2014.
SHAN D. A study of the effect of exit strategy on birandom safety-first portfolio model[D]. Chongqing: Chong-qing University, 2014 (in Chinese).
[11] 潘文超. 应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J]. 太原理工大学学报(社会科学版), 2011, 29(4): 1-5.
PAN W C. Using fruit fly optimization algorithm optimized general regression neural network to construct the operating performance of enterprises model[J]. Journal of Taiyuan University of Technology(Social Sciences Edition), 2011, 29(4): 1-5 (in Chinese).
[12] 霍慧慧. 果蝇优化算法及其应用研究[D]. 太原: 太原理工大学, 2015.
HUO H H. Research on fruit fly optimization algorithm and its applications[D]. Taiyuan: Taiyuan University of Technology, 2015 (in Chinese).
[13] 周平, 白广忱. 基于神经网络与果蝇优化算法的涡轮叶片低循环疲劳寿命健壮性设计[J]. 航空动力学报, 2013, 28(5): 1013-1018.
ZHOU P, BAI G C. Robust design of turbine-blade low cycle fatigue life based on neural networks and fruit fly optimization algorithm[J]. Journal of Aerospace Power, 2013, 28(5): 1013-1018 (in Chinese).
[14] 杜晓东. 果蝇优化算法在配电网规划中的应用[D]. 北京: 华北电力大学, 2014.
DU X D. The application of fruit fly optimization algorithm in distribution network planning[D]. Beijing: North China Electric Power University, 2014 (in Chinese).
[15] 毛正阳, 方群, 李克行,等. 应用改进果蝇优化算法的月面巡视器路径规划[J]. 中国空间科学技术, 2014, 5: 87-93.
MAO Z Y, FANG Q, LI K X, et al. Path planning for lunar rover based on modified fruit fly optimization algorithm[J]. Chinese Space Science and Technology, 2014, 5: 87-93 (in Chinese).
[16] SHAN D, CAO G H, DONG H J. LGMS_FOA: An improved fruit fly optimization algorithm for solving optimization problems[J]. Mathematical Problems in Engineering, 2013(7): 1256-1271.
[17] 韩俊英, 刘成忠. 反向认知的高效果蝇优化算法[J]. 计算机工程, 2013, 39(11): 223-225.
HAN J Y, LIU C Z. Efficient fruit fly optimization algorithm with reverse cognition[J]. Computer Engineering, 2013, 39(11): 223-225 (in Chinese).
[18] YUAN X F, DAI X S, ZHAO J Y, et al. On a novel multi-swarm fruit fly optimization algorithm and its application[J]. Applied Mathematics and Computation, 2014, 233: 260-271.
[19] 韩俊英, 刘成忠. 自适应混沌果蝇优化算法[J]. 计算机应用, 2013, 33(5): 1313-1316.
HAN J Y, LIU C Z. Adaptive chaos fruit fly optimization algorithm[J]. Journal of Computer Application, 2013, 33(5): 1313-1316 (in Chinese).
[20] 郑晓龙, 王玲, 王圣尧. 求解置换流水线调度问题的混和离散果蝇算法[J]. 控制理论与应用, 2014, 31(2): 159-164.
ZHENG X L, WANG L, WANG S Y. A hybrid discrete fruit fly optimization algorithm for solving permutation flow-shop scheduling problem[J]. Control Theory & Applications, 2014, 31(2): 159-164 (in Chinese).
[21] 雷开友, 邱玉辉, 贺一. 一种优化高维复杂函数的PSO算法[J]. 计算机科学, 2006, 33(8): 202-205.
LEI K Y, QIU Y H, HE Y. An effective particle swarm optimizer for solving complex functions with high dimensions[J]. Computer Science, 2006, 33(8): 202-205 (in Chinese).
[22] PAN Q K, SANG H Y, DUAN J H, et al. An improved fruit fly optimization algorithm for continuous function optimization problems[J]. Knowledge-Based Systems, 2014, 62(5): 69-83.
[23] 王建军, 高正红. Hicks-Henne翼型参数化方法分析及改进[J]. 航空计算技术, 2010, 40(4): 46-49.
WANG J J, GAO Z H. Analysis and improvement of Hicks-Henne airfoil parameterization method [J]. Aeronautical Computing Technique, 2010, 40(4): 46-49 (in Chinese).
[24] HICKS R M, HENNE P A. Wing design by numerical optimization[J]. Journal of Aircraft, 1978, 15(7): 407-413.
[25] COOK P H, MCDONALD M A, FIRMIN M C P. Aerofoil RAE 2822-Pressure distributions, and boundary layer and wake measurements: AGARD Report AR 138[R]. Paris: AGARD, 1979.
Animprovedfruitflyoptimizationalgorithmanditsapplicationinaerodynamicoptimizationdesign
TIANXu,LIJie*
SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China
Asanewswarmintelligenceoptimizationalgorithm,fruitflyoptimizationalgorithm(FOA)hasagoodpropertyofglobalconvergence.InordertofurtherimprovethesearchingperformanceofFOAanduseitforaerodynamicoptimizationdesign,anewalgorithmnamedimprovedfruitflyoptimizationalgorithm(IFOA)ispresented.ThesearchstepismodifiedbyintroducinganinertiaweightfunctiontoIFOA,andthedynamicalbalancebetweentheglobalandthelocalsearchissatisfied.Thesearchingefficiencyandaccuracyofalgorithmisintegrallyimproved.Formulti-dimensionalproblems,onlyonedecisionvariantisrandomlychangedforproducinganewsolutionineachsearch,andthenanewindividualfruitflyisproducedtogiveasearchbycombiningallexcellentindividualsintheiteration.Theconvergencespeedcanthusbegreatlyaccelerated.FunctiontestresultsshowthatIFOAhasobviouslyimprovedthesearchingperformanceofFOA.IFOAisappliedtoaerodynamicoptimizationdesign,andtheexamplesofairfoilinversedesignandsingle/multi-objectiveoptimizationdesigndemonstratethatIFOAisasimpleandefficientoptimizationmethod,andcanbewidelyusedinaerodynamicoptimizationdesign.
fruitflyoptimizationalgorithm;smellconcentration;searchstep;airfoil;aerodynamicoptimizationdesign
2016-04-27;Revised2016-05-26;Accepted2016-06-16;Publishedonline2016-06-231545
URL:www.cnki.net/kcms/detail/11.1929.V.20160623.1545.002.html
s:NationalNaturalScienceFoundationofChina(11172240);AeronauticalScienceFoundationofChina(2014ZA53002);NationalBasicResearchProgramofChina(2015CB755800)
2016-04-27;退修日期2016-05-26;录用日期2016-06-16; < class="emphasis_bold">网络出版时间
时间:2016-06-231545
www.cnki.net/kcms/detail/11.1929.V.20160623.1545.002.html
国家自然科学基金 (11172240); 航空科学基金 (2014ZA53002); 国家“973”计划 (2015CB755800)
*
.E-maillijieruihao@163.com
田旭, 李杰. 一种改进的果蝇优化算法及其在气动优化设计中的应用J. 航空学报,2017,38(4):120370.TIANX,LIJ.AnimprovedfruitflyoptimizationalgorithmanditsapplicationinaerodynamicoptimizationdesignJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):120370.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0198
V211.4
A
1000-6893(2017)04-120370-11
(责任编辑: 李明敏)
*Correspondingauthor.E-maillijieruihao@163.com

