板式无砟轨道系统对不同抗震体系铁路桥梁纵向地震响应的影响

张永亮，于伟栋，马华军，陈兴冲，刘尊稳



板式无砟轨道系统对不同抗震体系铁路桥梁纵向地震响应的影响

张永亮，于伟栋，马华军，陈兴冲，刘尊稳

(兰州交通大学土木工程学院，甘肃兰州，730070)

以某高速铁路大跨度连续梁桥及32 m简支梁桥为研究对象，针对CRTSⅡ型板式无砟轨道体系的结构特点，建立考虑轨道体系纵向约束及摩擦效应的线桥一体化计算模型，对2种不同的抗震体系(延性抗震体系及减隔震体系)进行非线性地震响应分析。研究结果表明：在剪力齿槽弹性工作状态下，轨道体系纵向刚度约束效应对桥梁下部结构地震反应的影响显著，但摩擦效应影响较小，可忽略。桥梁采用的抗震体系不同，在地震作用下轨道系统及剪力齿槽的受力及分布规律也不同。建议强震作用下板式无砟轨道体系的受力分析应合理考虑桥梁不同抗震体系的受力特征。最邻近连续梁的一跨简支梁的剪力齿槽水平剪力远大于其他跨简支梁的剪力，建议该跨的剪力齿槽应加强设计，以避免在地震作用下由于该处剪力齿槽的受力失效导致其他各剪力齿槽的连锁破坏。

铁路桥梁；地震反应；线桥一体化模型；板式无砟轨道；减隔震体系；延性体系

对于铺设有砟轨道的普通铁路桥梁，因道砟为散粒体，刚度较小且离散性大，对桥梁纵向地震反应的影响相对较小，故早期铁路桥梁抗震设计较少考虑线路对桥梁的约束作用[1]。但目前高速铁路桥梁广泛采用纵连板式无砟轨道体系及无缝线路，由于轨道系统纵向刚度较大，在一定程度上对桥梁起到纵向约束的作用，将各联桥梁联系成为一个弱耦合的连续结构，加强了桥梁的整体性，可能对桥梁的地震反应会产生一定的影响[2]。现行GB50111—2006“铁路工程抗震设计规范”[3]在桥梁地震反应分析模型方面，对板式无砟轨道体系是否考虑、如何考虑，尚无规定。自2000年以来，国内许多研究人员基于“梁轨相互作用理论”建立了地震下线桥一体化动力分析模型[4]。文献[5−6]的研究表明：轨道约束对桥梁纵向动力特性的影响不可忽略。文献[7]分析了有砟轨道系统对客运专线32 m减隔震体系简支梁桥地震反应的影响，结果表明轨道对主梁纵向地震位移、减隔震支座的位移及其累计耗能有一定影响。文献[8]研究了有砟轨道系统对普通铁路32 m延性体系简支梁桥纵向地震反应的影响，结果表明当桥墩刚度相差较大时，轨道约束影响较显著。文献[9]的研究表明，地震作用下大跨桥梁梁缝处钢轨最大纵向力比按规范伸缩工况计算值大很多，铁路桥梁抗震设计时需考虑轨道的约束作用。文献[10−11]采用反应谱法研究了多遇地震下CRTSⅡ型板式无砟轨道对多跨简支梁桥地震反应的影响。目前我国高速铁路桥梁主要采用2种抗震体系：延性抗震体系及减隔震体系。本文作者以某高速铁路大跨度连续梁桥及32 m简支梁桥为研究对象，针对CRTSⅡ型板式无砟轨道体系的结造特点，建立线桥一体化分析模型。采用非线性时程反应分析方法研究了罕遇地震作用下轨道约束体系对不同抗震体系桥梁下部结构地震反应的影响，并分析不同的抗震体系对桥上轨道系统纵向地震响应的影响。

1 罕遇地震下CRTSⅡ型无砟轨道体系建模

桥上CRTS II型板式无砟轨道由钢轨、弹性扣件、轨道板、砂浆调整层、连续底座板、滑动层等部分组成[12]。底座板在每孔梁固定支座上方设置剪力齿槽，通过锚固钢筋将底座板与主梁锚固在一起，以保证将线路系统纵向力直接传递给桥墩，其余部位设两布一膜滑动层。桥台后路基上设置摩擦板、端刺及过渡板，将底座板传递过来的纵向力锚定在路基上。分析CRTS II型板式无砟轨道的结构特点可知，罕遇地震作用下该轨道体系对桥梁结构的影响主要有2种效应：纵向刚度约束效应及摩擦效应。在线桥一体化模型中，应合理考虑这2部分效应。罕遇地震下CRTSⅡ型无砟轨道体系建模要点如下。

1) 钢轨、轨道板与底座板的模拟。以双线高速铁路桥梁为例，因仅考虑轨道约束对桥梁纵向地震反应的影响，根据几何特性等效原则可分别将4根钢轨、2块轨道板与底座板分别集成为2个整体截面，采用二维梁单元模拟。

2) 弹性扣件及两布一膜滑动层的模拟。线路纵向阻力是无缝线路的1个关键设计参数。长轨线路纵向阻力通常取扣件阻力，采用非线性阻力模型中的理想弹塑性模型。两布一膜滑动层根据库仑摩擦原理，也采用理想弹塑性模型。

3) 剪力齿槽的模拟。剪力齿槽采用纵向线性弹簧模拟，刚度取值为1.0×1010N/m[11]。

4) 端刺的模拟。主端刺纵向刚度取1.0×1010N/m[13]，桥台与端刺之间铺设的摩擦板长度按100 m考虑，则主端刺与摩擦板串联后刚度为7.6×108N/m，采用纵向线性弹簧模拟。

根据CRTS II型板式无砟轨道的结构特点，本文提出了罕遇地震作用下的线桥一体化分析模型，见图1。该模型主要用于计算沿桥梁纵向输入地震动时结构的地震响应。图2所示为忽略轨道约束影响的传统计算模型。

图1 线桥一体化计算模型

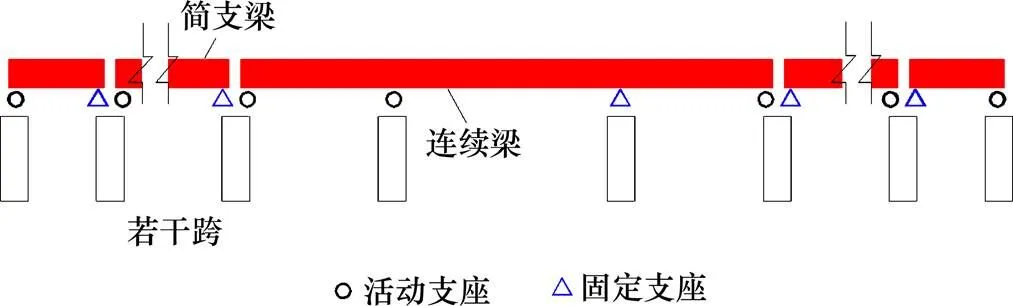
图2 传统计算模型

2 工程概况

某高速铁路大桥主桥为(80+128+80) m双线连续箱梁桥，立面布置见图3。主梁采用单箱单室截面，箱梁顶板宽为13.4 m，底板宽为7.0 m，跨中梁高为5.6 m，中墩处梁高为9.6 m，梁底按二次抛物线型渐变。下部结构为圆端形实体桥墩(纵、横向尺寸分别为4.5 m和11.6 m)，基础为24根直径1.5 m、桩长73 m的钻孔灌注桩。12号墩为制动墩。桥上二期恒载为210 kN/m。

单位：m

主桥两侧引桥为10跨32 m混凝土简支箱梁桥，主梁采用单箱单室截面，梁高3.08 m。墩身为矩形重力式桥墩(纵向×横向尺寸为2.5 m×6.0 m)，墩高为15.5 m，基础为8根直径1.25 m、桩长40 m的钻孔灌注桩。桥上二期恒载为120 kN/m。为叙述方便，各墩从左向右依次编号为：简支梁桥墩(1~9号)、连续梁桥墩(10~13号，其中10和13号为交界墩，12号为制动墩)、简支梁桥墩(14~22号)。

桥上轨道板及底座板混凝土强度等级分别为C60和C30, 单线截面长×宽分别为2.55 m×0.23 m和2.95 m×0.19 m, 钢轨采用60 kg/m钢轨，双线轴向等效刚度为8.28×1010N/m，等效质量为 5.8 t/m。

场地类别为Ⅱ类，特征周期分区二区，场地特征周期为0.4s。罕遇地震水平地震加速度=0.38。1条典型的罕遇地震安评波见图4。按传统计算模型计算得到简支梁与连续梁的纵向一阶自振周期分别为0.747 s和0.653 s。

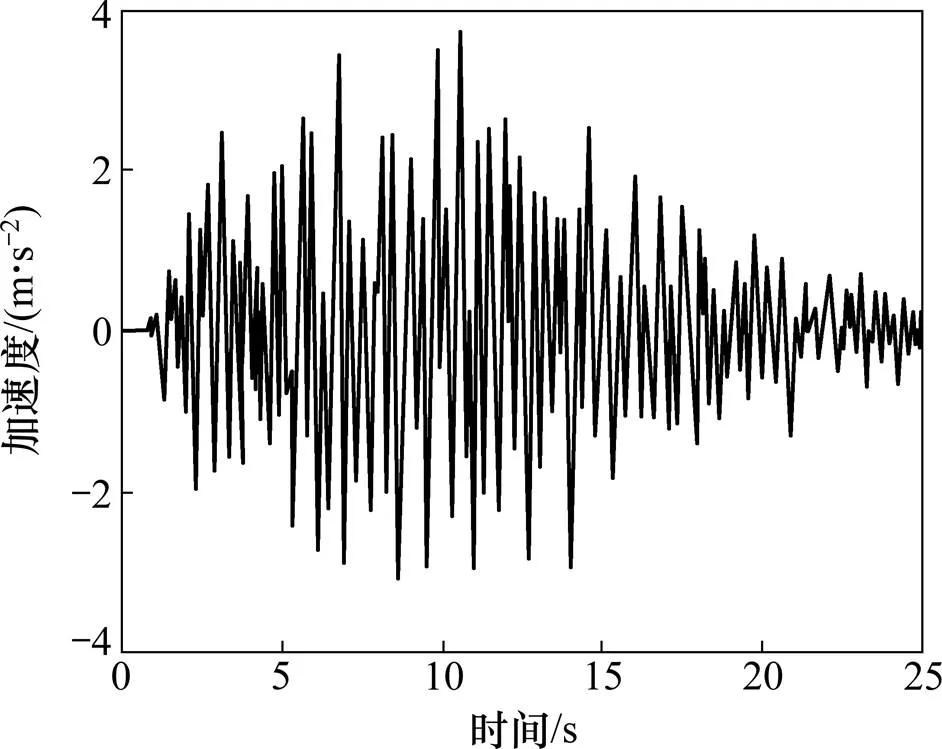
图4 典型的罕遇地震加速度时程曲线

3 轨道约束对减隔震体系桥梁地震反应的影响

桥梁减隔震体系指在地震作用下，桥梁上、下部连接构件发生塑性变形，延长结构周期，从而减小结构地震反应[14]。近年来双曲面球形减隔震支座在公路、铁路桥梁中应用较多，该类型支座利用钟摆原理实现减隔震功能，通过滑动界面摩擦消耗地震能量实现减震功能，通过球面摆动延长梁体运动周期实现隔震功能。在固定支座设置抗剪栓提高支座初始刚度以满足铁路桥梁行车安全性的要求。本文拟在连续箱梁桥上设置双曲面球形减隔震支座，在简支梁桥上设置普通盆式橡胶支座。

相关研究结果表明：双曲面球形减隔震支座的耗能能力稳定，滞回曲线饱满。一般可采用双线性模型模拟，见图5。影响该支座减隔震性能的主要参数为球面曲率半径、滑动面摩擦因数。本文双曲面球形支座的主要力学参数取值见表1。

图5 双曲面球型支座滞回曲线

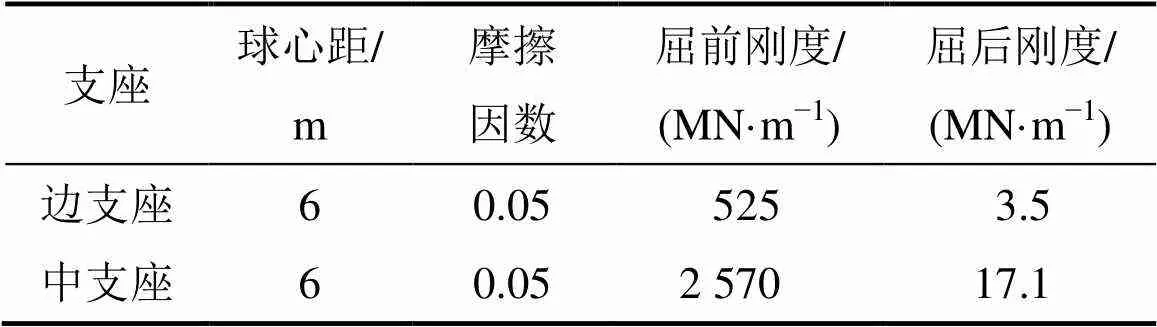
表1 双曲面球型支座的力学参数力学参数

轨道扣件主要考虑WJ7和WJ8型小阻力及常阻力扣件，轨道扣件以及两布一膜滑动层的力学参数取值见表2[15−16]。对桥梁减隔震体系共分析5种工况，其中，工况1~4为线桥一体化减隔震桥梁计算模型，这些工况假定轨道纵向约束刚度不变，仅改变轨道扣件及滑动层的摩擦参数；工况4相当于仅考虑轨道约束的纵向刚度，忽略摩擦；工况5为不考虑轨道体系的传统减隔震桥梁计算模型。

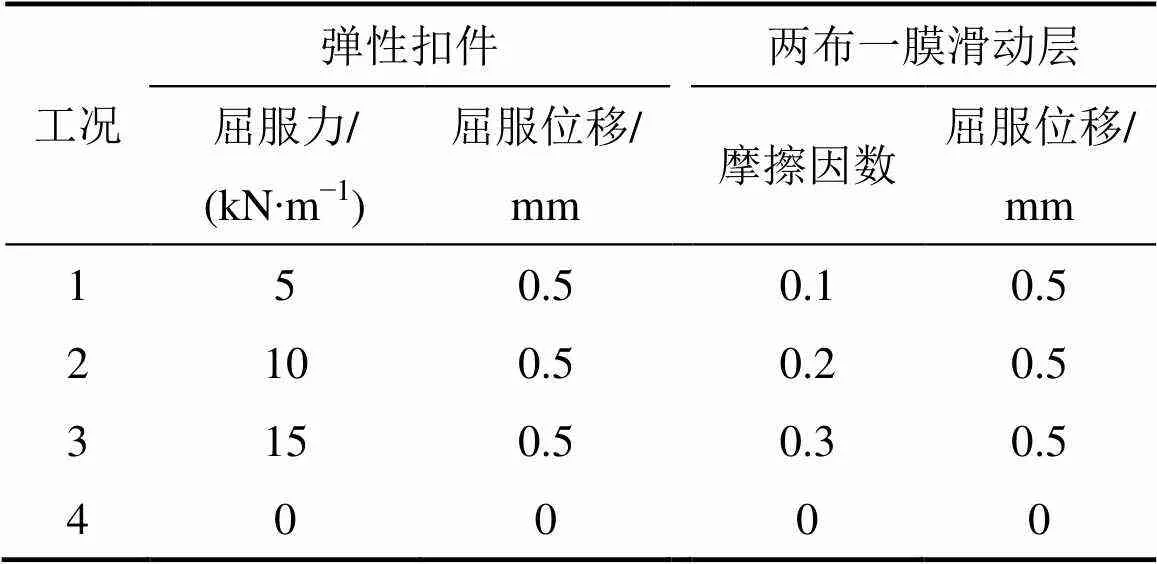
表2 扣件及滑动层力学参数

采用Midas civil软件对连续梁及简支梁桥建立全桥有限元计算模型。主梁及桥墩根据实际桥梁的尺寸建模，采用二维梁单元模拟。考虑地基的柔性作用效应，在承台底施加3个线性弹簧模拟地基刚度，其中弹簧参数采用法计算。假定桥墩均处于弹性工作状态。有限元计算模型见图6。进行非线性时程反应分析时，结构的阻尼采用Rayleigh阻尼矩阵，应用Newmark-β法逐步积分求解，分析时间步长为0.02 s。沿桥纵向输入3条罕遇地震下的安评地震波，结构地震响应选取3条波计算结果的平均值。

在上述工况下，各墩底截面弯矩分析结果见图7。轨道板轴力、钢轨轴力以及剪力齿槽水平剪力沿桥长方向的分布规律分别见图8~10。

1) 对比工况1~工况5计算结果，在剪力齿槽弹性工作状态下，轨道体系纵向刚度约束效应对桥墩墩底弯矩的影响显著，而摩擦效应影响相对较小。随着轨道体系摩擦因数的增大，桥墩地震内力有所降低。

2) 相对于工况5(传统减隔震计算模型)，在工况1~4下简支梁桥各墩墩底弯矩降低较多，约为工况5的53%~70%。而连续梁桥交界墩(10号和13号)的墩底弯矩增幅较大，约增大至工况5的1.8倍，12号制动墩的减震效果非常显著。简支梁桥地震反应降低原因为：由于连续梁桥跨度较大，上部一联梁体的质量较大，而制动墩相对较矮，采用双曲面球形减隔震支座后连续梁桥由隔震前0.89 s延长至4.86 s，连续梁桥动力特性的改变延长了整个桥梁体系的自振周期。

3) 轨道板轴力在各剪力齿槽处发生突变，在连续梁制动墩顶处达到最大值，而后向两端简支梁侧逐渐递减。钢轨轴力从简支梁侧开始逐渐增大，至连续梁交界墩(10号和13号)处达到最大值，而后向连续梁制动墩处逐渐减小至最小值。

4) 轨道体系摩擦因数对轨道板最大轴力的影响相对较小，但对钢轨轴力的最大值及其分布规律影响较大。随着摩擦因数的增加，钢轨轴力最大值降低较显著，由工况1的2 658 kN降低至工况3的2 069 kN，减小了23%，说明采用小阻力扣件可有效降低钢轨的地震反应，减小了地震作用下断轨或胀轨跑道的可 能性。

图6 有限元计算模型

1—工况1；2—工况2；3—工况3；4—工况4；5—工况5。

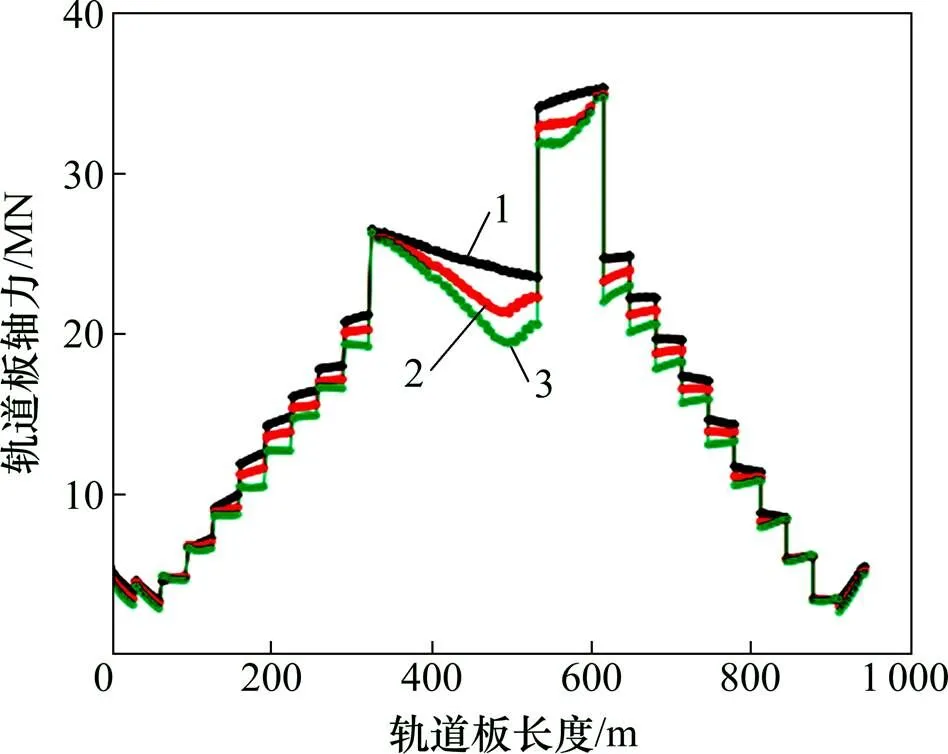
1—工况1；2—工况2；3—工况3。

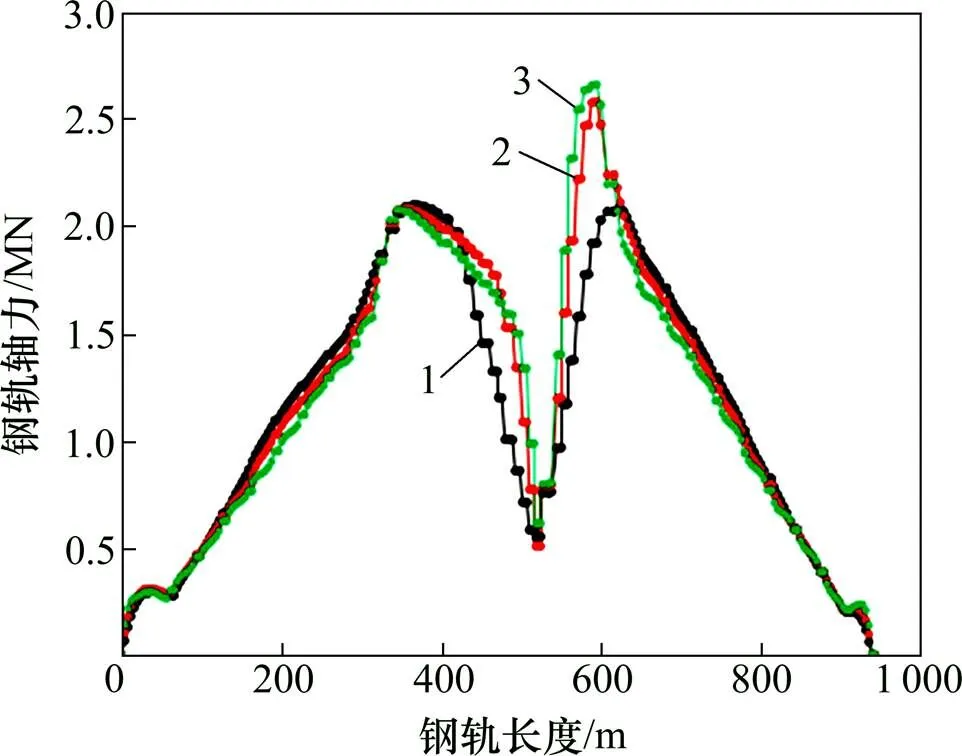
1—工况1；2—工况2；3—工况3。

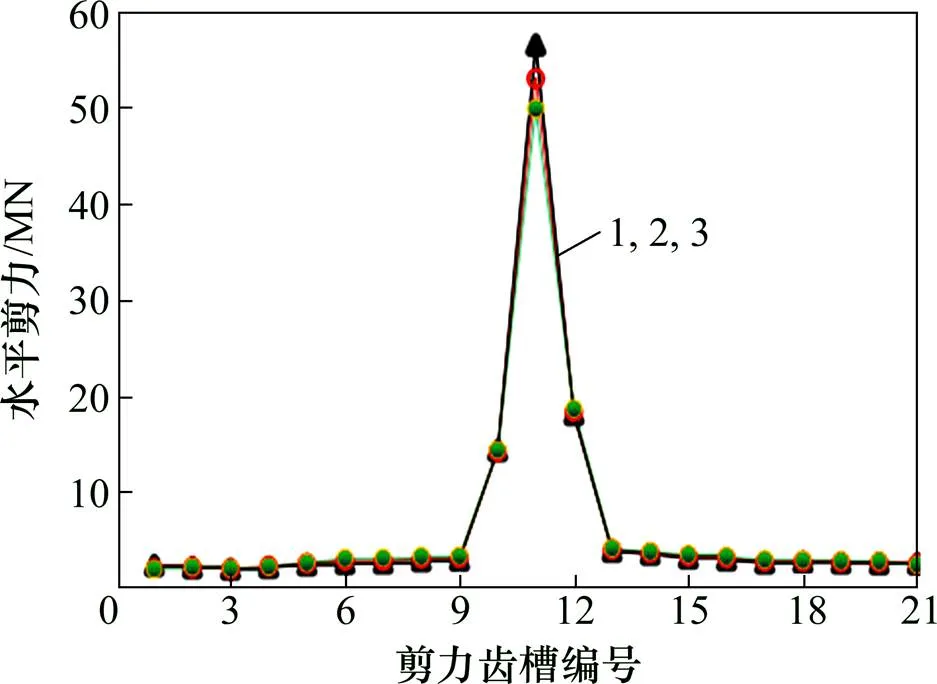
图10 各工况下剪力齿槽水平剪力分布

5) 轨道体系摩擦因数对剪力齿槽水平剪力量值的影响相对较小。但在与连续梁最近的一跨简支梁桥的剪力齿槽水平剪力(如13号墩18.0 MN)远大于其他简支梁桥的剪力(如14号墩4.1 MN)，这一点在设计中应引起注意。

4 轨道约束对延性体系桥梁地震反应的影响

桥梁延性抗震体系指在地震下利用桥梁墩柱发生塑性变形，延长结构周期，耗散地震能量[17]。本文拟在连续箱梁桥上设置普通球形钢支座，仅设一个制动墩(12号)，在简支梁桥上设置普通盆式橡胶支座。支座的传力关系根据支座的活动类型采用耦合不同自由度的方式实现。假定连续梁制动墩、简支梁桥墩的纵筋配筋率分别为0.65%和0.55%，配箍率按现行规范规定设置，钢筋采用HRB335。在各墩底设置塑性铰，塑性铰的滞回规则采用Clough 模型。其弯矩−曲率关系曲线采用Ucfyber软件计算，钢筋应力−应变关系应用曲线强化模型，保护层及约束混凝土应力−应变关系采用Mander模型。弯矩−曲率关系曲线控制点坐标见表3。

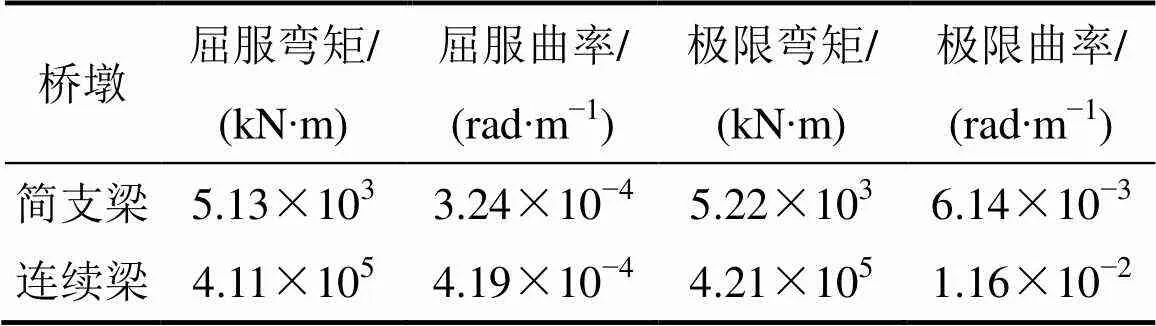
表3 墩底截面弯矩−曲率关系

对桥梁延性抗震体系共分析了4种工况：工况1~3为线桥一体化延性体系桥梁计算模型(轨道参数取值见表2)；工况4为不考虑轨道体系的传统抗震桥梁计算模型。在上述工况下，各墩底截面曲率分析结果见图11。轨道板轴力、钢轨轴力以及剪力齿槽水平剪力沿桥长方向的分布规律分别见图12~14。根据图11~14的计算结果可知：

1) 对比工况1~4计算结果可知：在剪力齿槽弹性工作状态下轨道体系纵向刚度约束效应对桥墩墩底曲率影响显著，而摩擦效应影响相对较小。考虑轨道约束简支梁桥墩底曲率降低明显。

2) 轨道板及钢轨轴力的分布规律与桥梁减隔震体系基本相同，但最大数值均较桥梁减隔震体系有较大幅度降低，轨道板及钢轨轴力分别降低了50%以上。表明桥梁抗震体系不同，对轨道系统的地震反应影响较大。

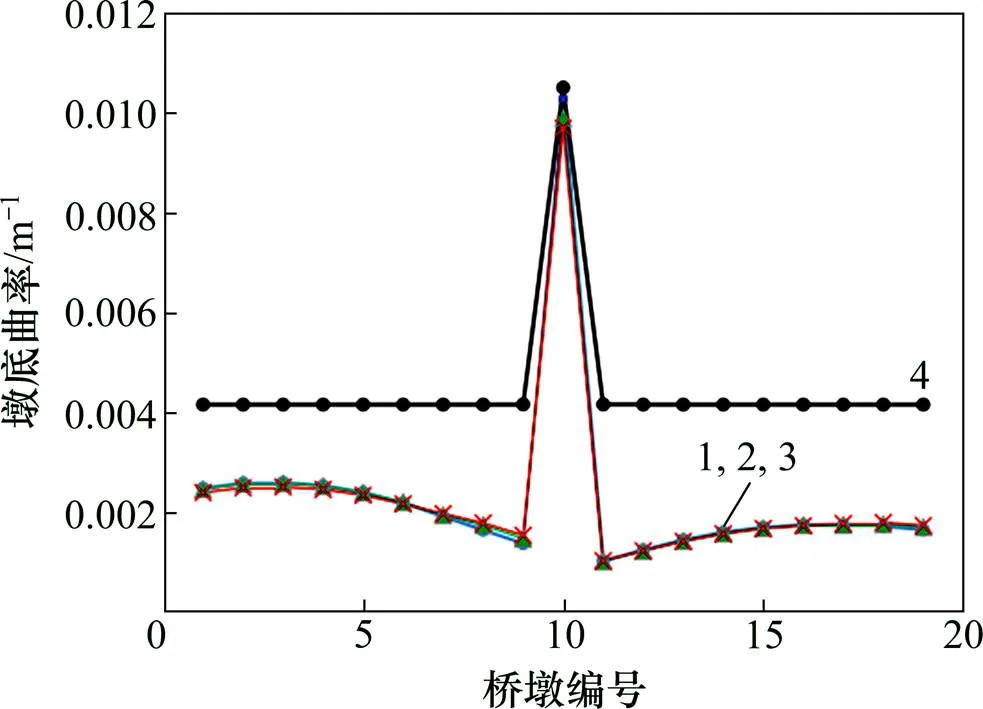
1—工况1；2—工况2；3—工况3；4—工况4。

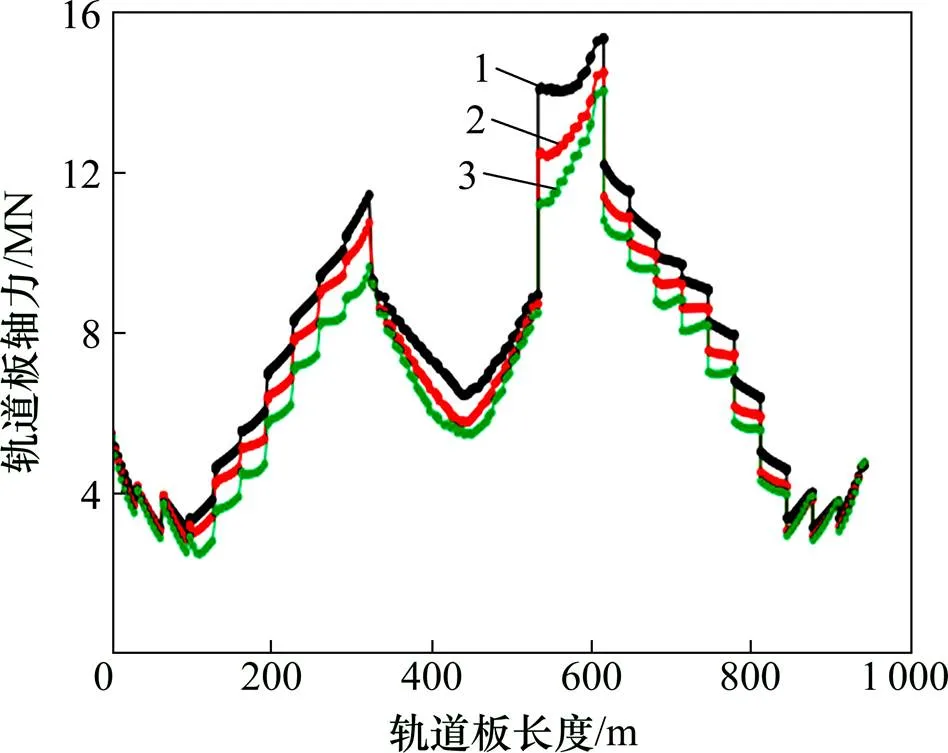
1—工况1；2—工况2；3—工况3。

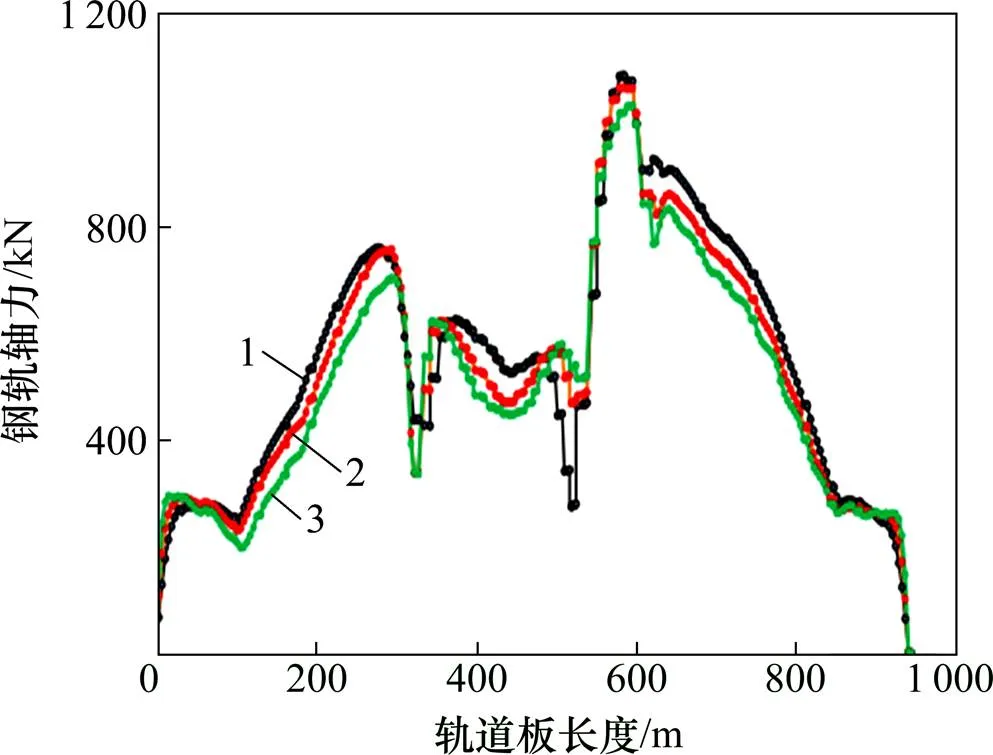
1—工况1；2—工况2；3—工况3。

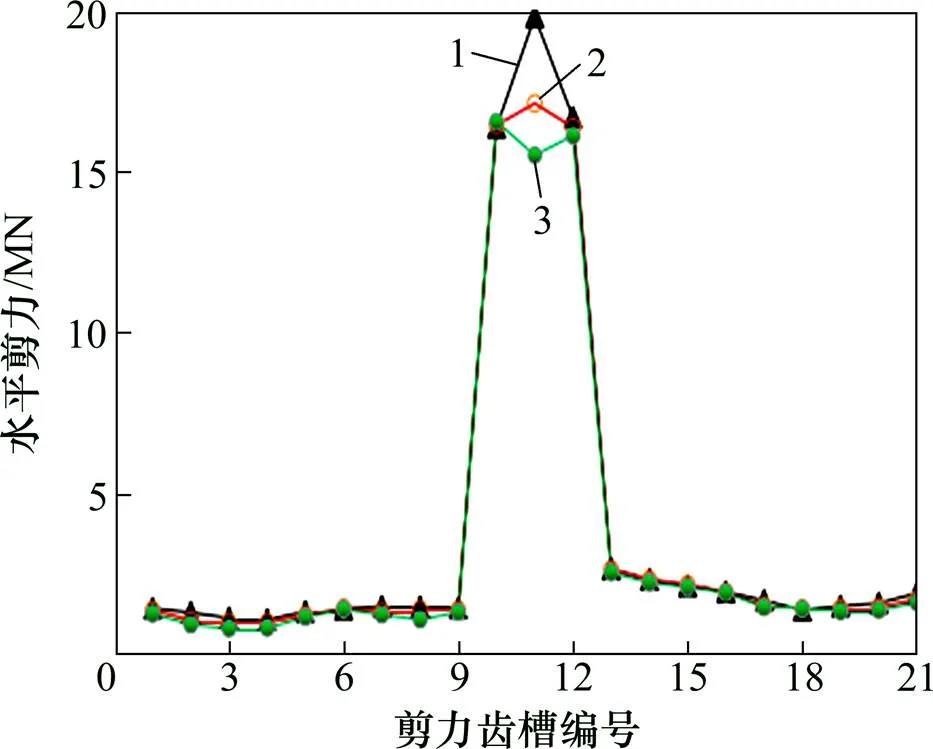
1—工况1；2—工况2；3—工况3。

3) 轨道体系摩擦因数对连续梁制动墩剪力齿槽水平剪力有一定的影响。采用延性抗震体系时的连续梁制动墩处的剪力齿槽水平剪力为19 810 kN，约为减隔震体系的35%(56 360 kN)。但在与连续梁最近的一跨简支梁桥的剪力齿槽水平剪力(如13号墩16 100 kN)仍远大于其他简支梁桥的剪力(如14号墩2 500 kN)。

5 结论

1) 对于CRTSⅡ型无砟轨道体系，在剪力齿槽弹性工作状态下，轨道体系纵向刚度约束效应对桥梁下部结构地震反应的影响显著。轨道扣件及两布一膜滑动层的摩擦效应对桥梁下部结构的影响相对较小，但对轨道体系的受力影响较大。当仅考虑轨道体系对桥梁下部结构的影响时，可忽略其摩擦效应。

2) 对于CRTSⅡ型无砟轨道体系，桥梁采用的抗震体系不同，在地震作用下轨道系统及剪力齿槽的受力大小及分布规律不同。对于本文算例，延性抗震体系时的轨道系统受力明显比减隔震体系的低。因此，建议地震作用下轨道体系受力分析应合理考虑桥梁不同抗震体系的受力特征。

3) 采用小阻力扣件可有效降低钢轨的地震反应，减小了地震作用下断轨或胀轨跑道的危险性。

4) 不管采用何种抗震体系，邻近连续梁最近的那一跨简支梁的剪力齿槽水平剪力远大于其他跨简支梁的剪力。建议此跨简支梁的剪力齿槽应加强设计，以避免在地震作用下由于该处剪力齿槽的受力失效导致其他各剪力齿槽的连锁破坏。

[1] 黄宇辰, 王军文, 王少君. 无砟轨道约束对高铁FPS隔震简支梁桥纵向地震反应的影响[J]. 铁道建筑, 2015(9): 24−28. HUANG Yuchen, WANG Junwen, WANG Shaojun. Influence of ballastless track constraints on the longitudinal seismic response of high-speed FPS isolated bridges[J]. Railway Engineering, 2015(9): 24−28.

[2] 刘朝, 成诚. 长轨高速铁路桥梁地震响应研究[J]. 中国水运, 2015, 15(7): 225−227. LIU Zhao, CHENG Cheng. Study on seismic response of long rail high-speed railway bridges[J]. China Water Transport, 2015, 15(7): 225−227.

[3] GB 50111—2006, 铁路工程抗震设计规范[S]GB 50111—2006, Code for seismic design railway engineering[S].

[4] YAN Bin, DAI Gonglian, ZHANG Huaping. Beam-track interaction of high-speed railway bridge with ballast track[J]. Journal of Central South University, 2012, 19(5): 1447−1453.

[5] 黄勇, 王君杰. 轨道约束对城市轨道交通高架桥地震反应的影响[J]. 地震工程与工程振动, 2014, 34(4): 228−234. HUANG Yong, WANG Junjie. Effects of rail system restraints on seismic responses of mass transit viaducts[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(4): 228−234.

[6] TOYOOKA A, IKEDA M, YANAGAWA H, et al. Effects of track structure on seismic behavior of isolation system bridges[J]. Quarterly Report of RTRI, 2005, 46(4): 228−243.

[7] 黄艳, 阎贵平, 刘林. 轨道约束对铁路桥梁纵向地震反应特性的影响[J]. 铁道学报, 2002, 24(5): 124−128. HUANG Yan, YAN Guiping, LIU Lin. Effects of rail restraints on longitudinal seismic response of railway bridges[J]. Journal of the China Railway Society, 2002, 24(5): 124−128.

[8] 谢旭, 王炎, 陈列. 轨道约束对铁路减隔震桥梁地震响应的影响[J]. 铁道学报, 2012, 34(6): 75−82.XIE Xu, WANG Yan, CHEN Lie. Effect of rail restraints on seismic responses of cushioning railway brides[J]. Journal of the China Railway Society, 2012, 34(6): 75−82.

[9] 严猛, 魏贤奎, 王平, 等. 大跨桥上无缝线路纵向地震响应研究[J]. 铁道学报, 2014, 36(5): 96−102. YAN Meng, WEI Xiankui, WANG Ping, et al. Research on longitudinal seismic responses of continuous welded rails on large-span bridges[J]. Journal of the China Railway Society, 2014, 36(5): 96−102.

[10] 张永亮, 陈兴冲, 李子奇. 轨道约束系统对高速铁路多跨简支梁桥地震反应的影响[J]. 世界地震工程, 2010, 26(4): 6−12. ZHANG Yongliang, CHEN Xingchong, LI Ziqi. Effects of rail system restrains on seismic response of multi-span simply supported girder bride on high-peed railway[J]. World Earthquake Engineering, 2010, 26(4): 6−12.

[11] 张永亮, 赵继栋, 陈兴冲, 等. 轨道约束对高铁大跨连续梁桥地震反应的影响[J]. 铁道工程学报, 2015(7): 47−50. ZHANG Yongliang, ZHAO Jidong, CHEN Xingchong, et al. Influence of track system restraint on seismic response of the high-speed railway long-span continuous girder bridge[J]. Journal of Railway Engineering Society, 2015(7): 47−50.

[12] 郑健.中国高速铁路桥梁[M]. 北京: 高等教育出版社, 2008: 505−513. ZHENG Jian. Chinese high-speed railway bridge[M]. Beijing, Higher Education Press, 2008: 505−513.

[13] 魏强, 赵国堂，蔡小培. CRTSⅡ型板式轨道台后锚固结构研究[J]. 铁道学报, 2013, 35(7): 90−95. WEI Qiang, ZHAO Guotang, CAI Xiaopei. Study on Anchor Structure behind the Abutment for Slab Track CRTSⅡ[J]. Journal of the China Railway Society, 2013, 35(7): 90−95.

[14] JT/T 927—2014, 桥梁双曲面球型减隔震支座[S].JT/T 927—2014, Double spherical seismic isolation bearing for bridges[S].

[15] 杨艳丽. WJ-7、WJ-8型扣件纵向阻力现场试验与研究[J]. 铁道标准设计, 2010(2): 51−52. YANG Yanli. Filed test and research of fastener longitudinal resistance on the WJ-7, WJ-8[J]. Railway Standard Design, 2010(2): 51−52.

[16] 贾梦雪. 桥上CRTSⅡ型板式无砟轨道纵向力影响因素分析[D]. 成都: 西南交通大学土木工程学院, 2010: 24−36. JIA Mengxue. Influential factors analysis of longitudinal force on bridges with CRTSⅡ-type slab ballastless track[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2010: 24−36.

[17] 范立础, 胡世德, 叶爱君. 大跨度桥梁抗震设计[M]. 北京: 人民交通出版社, 2001: 107−115. FAN Lichu, HU Shide, YE Aijun. Seismic design of long-span bridges[M]. BeiJing: China Communications Press, 2001: 107−115.

(编辑 杨幼平)

Influence of slab ballastless track on longitudinal seismic response of railway bridge with different seismic systems

ZHANG Yongliang, YU Weidong, MA Huajun, CHEN Xingchong, LIU Zhunwen

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Taking a long-span continuous girder and 32 m simply-supported beam bridge of the high speed railway as the research object, the rail-bridge integrated model was established considering longitudinal restraints and friction effects of track system according to structural characteristics of the CRTSⅡslab ballastless track system. Nonlinear seismic response analysis was carried out on two different seismic systems including ductility seismic system and seismic isolation system. The results show that when shear cogging is in elastic working state，longitudinal stiffness constraint effect of track system has significant effects on seismic response of bridge substructure. But friction effect can be ignored. Different seismic systems used in bridge substructure, the magnitude and distribution law of the force from track system and shear cogging are also different under earthquake. So it is recommended that track system force analysis should consider reasonably seismic systems of the bridge under intense earthquake. Horizontal shear of shear cogging in the simply-supported beam which is nearest to the continuous girder is much greater than that of other spans. So it is recommended that shear cogging design of this span should be strengthened in order to avoid chain failure of the other shear coggings resulting from failure of the one.

railwaybridge; seismic response; rail-bridge integrated model; slab ballastless track; seismic isolation system; ductility system

10.11817/j.issn.1672−7207.2017.10.025

U442.5

A

1672−7207(2017)10−2738−07

2016−11−03；

修回日期：2017−01−10

国家自然科学基金资助项目(51468031，51368034)；甘肃省科技计划项目(17JR5RA103)(Projects(51468031, 51368034) supported by the National Natural Science Foundation of China; Project(17JR5RA103) supported by the Science and Technology Plan of Gansu Province)

张永亮，博士，教授，从事桥梁抗震研究；E-mail：zhangyong_L@126.com