让学生经历“植树问题”反建模的过程
郜舒竹
【摘 要】将“植树问题”变为线段上点与间隔的关系问题,这样的过程称为建模的过程;反过来将线段上点与间隔的关系问题应用于更加广泛的实际情境中的过程,称为反建模的过程。在植树问题的学习活动设计中,学生不仅应当经历建模的过程,还应经历反建模的过程。
【关键词】数学学习活动 植树问题 栅栏柱问题 建模 反建模
“植树问题”在人教版教材《数学广角》的栏目中出现。利用植树的情境,区分“两端”以及道路“两侧”植树的不同情况,探讨植树棵数与植树间隔之间的关系问题。事实上,植树问题中的“植树”并不是这一问题的核心,在国外此类问题也称为“栅栏柱问题(Fencepost Problem)”,其核心是用数学中“点”与“间隔”的关系,澄清一些对于实际情境中经常出现的“误解(Misconception)”,修正由于误解而产生的错误。这样的过程也体现了建模(Modeling)与反建模(Inverse Modeling)的过程。
一、植树问题与反建模
小学数学课程中的“植树问题”通常表述为:在一条长度为8米的路上植树,每隔2米植树1棵。那么一共可以植树多少棵?这一问题极易产生误解,学生认为8除以2等于4为本题答案,而事实上4这一结果是树之间的间隔数,并不是植树棵数,间隔数比植树棵数少1。(见图1)
这种误解与错误实际上是将树的“棵”数与相邻树之间的“间隔(Span)”数混淆,出现“少1(Off-by-One)”的错误。
因此,学生学习植树问题的一个重要目的,应当是澄清误解、消除错误。将植树问题或栅栏柱问题转化为一条线段上“点”数与相邻两点之间的“间隔”数的关系问题,进而通过对这种关系的研究,澄清对植树问题的误解。如果把这样从实际情境到数学模型的过程叫作建模(Modeling)的过程,那么引导学生进一步经历将数学模型应用于更加广泛的实际情境的过程,就可以称之为“反建模”的过程。
二、计算时间的问题
在日常工作、生活中,类似于“植树问题”数量关系的情境经常出现,比如对于计算年龄的问题,如果要计算2017年国庆节是建国多少周年,采用的计算方法应当是,用今年的公元年数2017直接与建国公元年数1949相减,得到答案为68周年,即2017-1949=68(周年)。
与此类似的是计算天数的问题。比如,某人从2017年10月1日到10月7日外出旅游,那么本次旅游一共多少天?这样的情况,就不能用大数直接减去小数的方法计算,也就是不能用“7-1=6(天)”计算。
造成这种差异的根本原因在于“年龄”是“经过多少年”的含义,相当于植树问题中的“间隔”。而旅游天数中的“天”是“当天”的含义,相当于植树问题中的“点”。需要注意,计算天数的问题,也经常出现“经过”的含义,比如宾馆住宿的天数计算,如果10月1日午夜12点前入住,10月7日中午12点前离开,那么住宿费用的计算就是按照“7-1=6(天)”计算,而不是按照7天计算。
因此,在“植树问题”数量关系的问题中,区分“点数”与“间隔数”需要根据实际情境进行判断。一个基本方法是看“起点”是“0”还是“1”,比如前面“多少周年”的问题,起点“1949”相当于年龄为“0年”,到1950年才视为经过1年,因此是“间隔”的问题。而旅游天数问题中起点10月1日已经算作“1天”,因此是“点数”的问题。而宾馆住宿天数计算时,10月1日入住当天视为“0天”,到10月2日第二天才视为住宿“1天”,因此也是“间隔”的含义。
三、计算楼层的问题
这种“点”与“间隔”关系的误解问题,在楼层表述时也经常出现。比如,2014年中央电视台春节联欢晚会上有一个由冯巩主演的、名为《我就这么个人》的小品节目,意在讽刺给领导送礼的社会现象。其中有一段冯巩与饰演搬运工人的曹随风的对话片段。
冯巩:就这个门,501。
曹随风:电梯了?
冯巩:没电梯,享受低碳生活。
曹随风:那你得给钱。
冯巩:给什么钱?
曹随风:爬楼钱。
冯巩:爬楼还要钱?
曹随风:一层20。
冯巩:瞎说,去年还15呢。
曹随风:涨价了,跟出租车一块涨的,你这是地上五层,你得给俺100。
提炼出这段对话中的算术过程应当是:现在每爬一层给“我”20元钱,要爬到五层,一共需要给“我”“20×5=100(元)”。这里显然混淆了“几层”与“爬几层”的概念,也即混淆了植树问题中“点”与“间隔”的概念。事实上,从1层楼爬到5层楼,经过的是“爬4层”的过程。(见图2)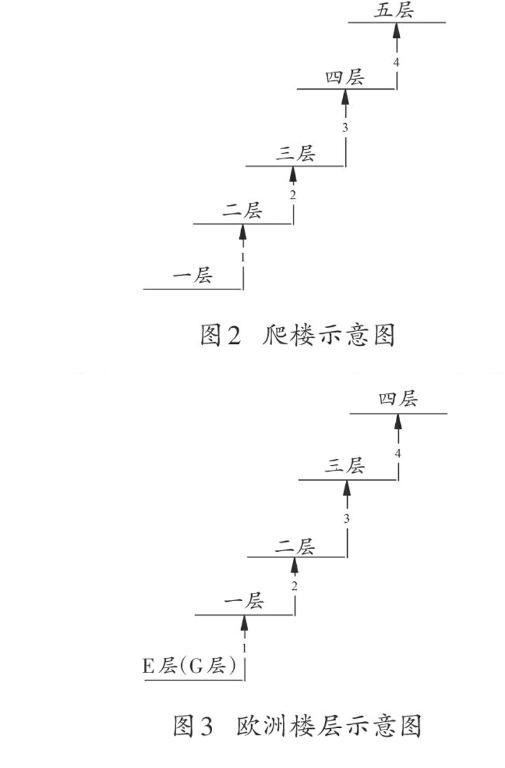
在欧洲一些国家,通常会把我们所说的“一层”叫作“E”或者“G”,其含义是“地面”,用英文单词“earth”或者“ground”的第一个字母代表。把我们所说的“二层”叫作“一层”,以此类推。这样的做法实质上是将起点视为“0层”,其优越性在于将“几层”与“爬几层”统一起来了。(见图3)
综上可以看出,在这种反建模的探究活动中,通过线段上点数与间隔数关系这一模型,可以进一步澄清并消除实际情境中更加广泛的误解和错误。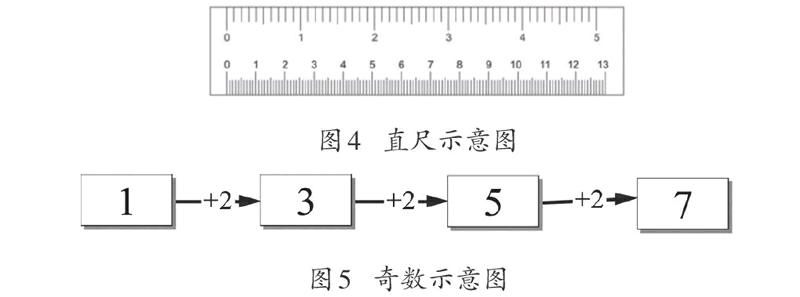
四、植树问题中的思想与方法
植树问题数量关系中蕴含着的思想方法,对于其他数学知识的思考与理解也是有益的。比如在中学数学中关于数轴的认识,按照通常的理解,数轴有“三要素”,分别是原点、单位和方向。其中的原点用数字“0”标记,而后自左向右依次标记数字1、2、3等。这类似于小学生所熟悉的直尺。(见图4)
一个自然的问题是,为什么数轴或者直尺的起点规定为“0”,而不是“1”?其原因之一就在于能够实現“点的标记”与“间隔”数量的统一。数轴上标记为5的点,同时也意味着这一点到起点的距离包含着5个单位。在直尺上标记为5厘米的点,也意味着这一点到起点“0”的距离是5厘米。其原理与图3所示欧洲楼层的标记是一致的。
这里实际上蕴含着“对立统一”的方法,直尺上的点的标记与这个点到起点的距离,原本是两个不同的概念,将起点标记为“0”,就实现了“变不同为相同”,也就是创造了将对立的双方相互转化的条件,实现了对立双方的统一。
这种线段上点数与段数的关系,还可以应用于高中数学课程中等差数列通项公式的学习。比如,如果把1视为第一个奇数,求第100个奇数是多少。这一问题实际上是寻找第100个奇数与第1个奇数之间的关系。先从简单情况入手看,在一条线段上标记出四个奇数1、3、5、7。(见图5)
图5中四个奇数相当于4个点,相邻2个奇数的线段是3条,每一条线段表示“加2”的意思,那么奇数从1变化到7,相当于加了3次2。因此奇数7与奇数1的关系可以表示为:
7=1+2×3
按照同样的思路,如果把从1开始的100个奇数标记在一条线段上,相当于有100个点,其中相邻两点的线段表示“加2”,一共99条这样的线段,相当于第100个奇数就是在1上加了99次2,因此这个奇数应当是:
1+2×99=199
如果把线段上“点”与“间隔”的关系视为植树问题的本质性内容,把人类日常活动中针对此类问题出现的误解视为文化性内容,让表面看与植树问题毫无关系的内容建立起联系,那这样的数学学习活动设计就做到了“突出本质、渗透文化、实现关联”。
(首都师范大学初等教育学院 100048)endprint

