在“立”与“破”中绽放精彩
孔忠伟
【摘 要】“梯形面积计算练习课”是人教版五年级上册第六单元的内容,教师可以让学生在不断的“立”与“破”中加深对梯形面积公式的理解,促进学生空间观念的发展。通过不断“立”新规、“破”新规,不断拓展梯形面积公式的运用范围,沟通不同公式之间、数与形之间的联系,有效提升学生对于梯形面积公式的理解与熟练程度,促进学生理解知识的本质,提升空间观念的发展。
【关键词】梯形面积公式 组合图形 等积变形
依據建构主义理论,知识的学习就是一个不断同化与顺化的过程。奥苏贝尔也讲过:“最有效的学习就是建立在学生原有经验基础之上。”因此,在课堂教学中,教师就需要深入了解学生已有基础,并在此基础上,不断去丰富与拓展知识,促进学生数学水平的发展。本文从梯形面积公式出发,不断让学生感受到梯形面积公式不仅可以计算梯形的面积,同时还可以计算其他平面图形的面积。不仅如此,它还可以解决组合图形,甚至计算数的问题等,从而帮助学生提升对于梯形面积公式的理解,沟通各图形之间的联系,促进学生几何直观与空间观念的发展。像这样的教学,其实就是在原有的基础上不断打破规则,建立新的规则,让学生在不断的“立”与“破”中感受乐趣,促进发展。
一“立”——梯形面积公式可以计算其他平面图形的面积
这里的“立”就是让学生了解梯形的面积公式除了可以计算梯形的面积,也可以计算其他平面图形的面积,如平行四边形、三角形、长方形等都可以看成是特殊的梯形,所以也可以用梯形面积来计算。这样的设计可以让学生打破原先的思路,促进学生对于梯形面积公式的深入理解,并沟通各平面图形面积计算之间的联系,促进学生几何直观能力的发展,所以我们设计了如下教学。
【教学片段】
师:同学们,请观察这些梯形,你发现了什么?
生:它们的高都一样,底也一样,所以面积也相等。
生:它们的形状不同,但面积都一样。
小结:虽然形状不同,但梯形面积都相等。
师:请你们再仔细观察,又发现了什么?
生:它们的形状不同,而且上底与下底的和都是10。
师:那它们的面积都相等吗?为什么?
生:都相等,只要上底与下底的和相等,高相等,它们的面积都相等。
小结:只要上底与下底的和相等,高相等,它们的面积也就相等。
师:哦!那么你们还能画出高相等,面积相等的梯形吗?(学生画一画)
展示一:
师:非常好!像这样的梯形,画得完吗?
生:画不完,因为上底与下底的和是10,但上底和下底可以随便变。
小结:只要上底与下底的和不变,就可以画出无数个不同形状面积相等的梯形。
师:嗯。有道理,那么除了梯形,你还能画出其他图形吗?(能)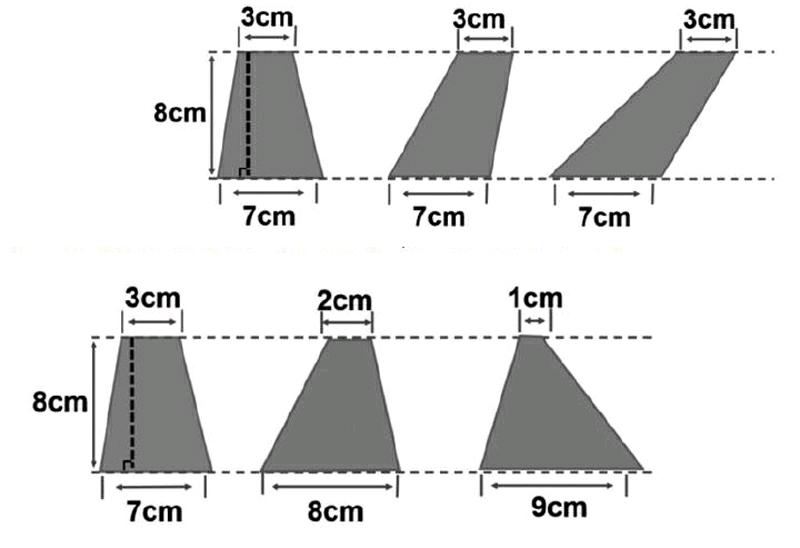
展示二:
师:你是怎么想的?
生:我把上底看成0厘米,下底看成10厘米,这样它们上底与下底的和还是10厘米,它们的面积也是不变的,所以面积也等于(0+10)×8÷2=40(平方厘米)。
生:我把上底看成5厘米,下底也看成5厘米,所以上底与下底的和还是10厘米,和也是不变的,所以面积也等于(5+5)×8÷2=40(平方厘米)
小结:是的。同学们,其实三角形、平行四边形和长方形等都可以看成是一种特殊的梯形,只要上底与下底的和相同,它们的面积也就相等。
通过两次对比与两次操作,让学生慢慢感受梯形面积的等积变形,让学生知道只要上底与下底的和不变,高不变,虽然形状会发现变化,但梯形的面积都不会发生变化,然后让学生在不断的讨论交流与操作中,逐渐联想到其他不同的图形,沟通梯形与其他平面图形之间的联系。在教学过程中,让笔者欣喜的是,学生不仅能够画出不同的图形,而且还能把三角形与平行四边形看成是一种特殊的梯形,这是一种多好的发现啊。相信通过这样不断的练习,学生的空间观念一定能够获得较大的提升。
二“立”——梯形面积公式可以计算组合图形面积
二“立”主要是指让学生了解梯形面积公式除了可以计算不同的图形面积,它还可以求组合图形的面积。通过让学生逆向从公式去找图形,使学生发现原来多个图形组合在一起也可以用梯形公式来解决,从而再次打破学生刚刚建立的规则,再一次使梯形的面积公式扩大到了计算组合图形的面积,这样不仅为后面组合图形面积的学习打下一定的基础,同时也有效促进学生空间观念的发展。
【教学片段】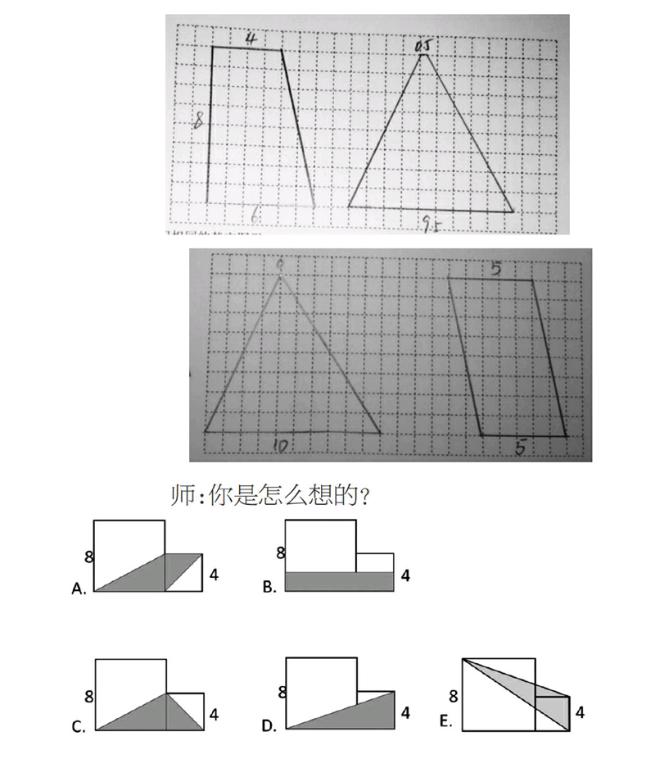
师:想一想,这会是怎样一个梯形?
师板书:S=(8+4)×4÷2
生:上底是4厘米,下底是8厘米,高是4厘米的梯形。
师:现在把这个图形放到了两个正方形中,仔细观察,你们觉得哪幅图也可以用这个算式表示?同桌间交流一下。
生:我觉得A可以表示。因为它就是一个梯形,它的上底是4厘米,下底是8厘米,高也是4厘米。
生:我觉得C和D也可以的,因为8+4=12厘米,而它们的底也是12厘米。
生:B也是可以的,因为它的长是12厘米,宽是4厘米的一半,也就是2厘米。
师:非常好!找到了很多不同情况,那么E可以吗?
生:不可以的,它的高不对。
生:应该可以的。
师:哦。那你能上来指一指吗?
生:好的。这个点可以移动,把它移到这里后,它的高也就是4+8=12厘米。所以也是可以的。endprint
小结:看来,梯形的面积公式除了可以解决其他图形的面积外,还可以解决类似的组合图形面积。
从上面教学中,我们发现有了前面环节的设计,大部分学生对于梯形面积的认识有了较大的提升。在一些组合图形中,学生会把一些长方形、三角形等看成特殊的梯形。同时,也有部分学生会从整体上去看待组合图形,并通过点或边的移动来进行想象与理解,从而再次促进了学生对于梯形面积公式的理解,同时也让学生感受到一些组合图形的面积只要符合梯形公式的要求,当然也可以用梯形面积公式来计算。
三“立”——梯形面积公式可以计算数的大小
三“立”主要指把梯形面积公式与以前数的计算联系起来,学生在四年级下册学习简便计算时,就有利用梯形面积公式计算数的经验。通过让学生观察回忆这些方法,帮助学生回顾旧知,可以有效地让计算数的方法与梯形面积公式建立联系,从而更好地建构知识,促进学生思维的发展。
【教学片段】
师:刚才利用梯形的面积公式,我们解决了很多图形的问题。那么想一想,以前我们学过的知识中,有没有也是利用梯形面积公式计算的?(学生思考)
师:老师收集了一些,我们一起来看一下。
课件出示:
(1+10)×10÷2=55(根) (1+20)×20÷2=210
师:从这里,你们发现了什么?
生:其实这木棒的上面就像是梯形的上底,下面就是梯形的下底,上底与下底之间就是高。利用梯形公式就可以算出木棒数量。
生:我发现第一个数与最后一个数相加,就像是上底加上下底,然后去乘高除以2。
小结:对!在我们的数学学习中,梯形面积公式不仅可以解决图形计算的问题,同时也可以用来解决一些数的问题。
在上面的教学中,通过先让学生回忆旧知,大部分学生还是无法把梯形面积公式与已有知识建立联系,因此需要教师进行有效的引导。通过让学生观察四下的求木棒图,巧算求和等问题,学生很快就发现它们其实与梯形面积的公式非常相似,通过把数与形建立有效的联系,有效提升了学生数形结合的能力以及几何直观的能力。
在数学知识的学习过程中,我们不仅要让学生不断把知识从薄学到厚,同时也要让他们把知识从厚学到薄,通过不斷沟通前后知识之间的联系,挖掘知识的本质,有效帮助学生更好地整合知识,促进其数学水平的真正有效发展。
(浙江省杭州市滨文小学 310000)endprint

