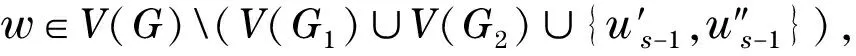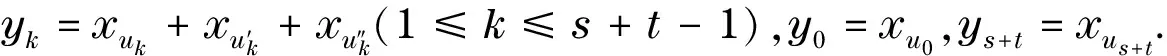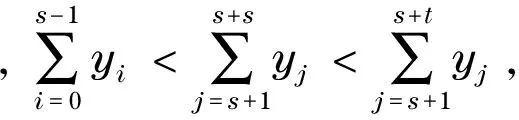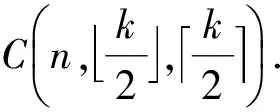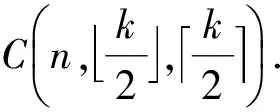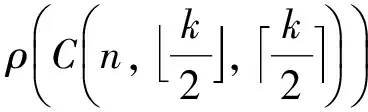4度点数固定的树的距离谱半径
,
(上海理工大学 理学院,上海 200093)
4度点数固定的树的距离谱半径
汪云,吴宝丰
(上海理工大学 理学院,上海200093)
引入了一种图的变换,得到了距离谱半径的变化规律.进一步研究了四度点数固定的树集,刻画了该图类中距离谱半径最大的极图.最后,讨论了更一般的图类,即度至少为4的点数固定的树集,并确定了极图.
距离矩阵; 距离谱半径; 距离Perron向量; 树
1 基本概念
研究的图均为连通的简单无向图.设G是n阶连通图,V(G)和E(G)分别是顶点集和边集.对于任意顶点v∈V(G),用NG(v)表示它的邻集,并根据其度数的奇偶性,称它为奇度点或偶度点.对于图G的任意2点u,v,用dG(u,v)表示它们的距离,D(G)=(dG(u,v))u,v∈V(G)表示图G的距离矩阵.显然,D(G)是实对称的,所以,它的特征值全为实数.图G的距离谱半径用ρ(G)表示,代表D(G)的最大特征值.连通图对应的距离矩阵是不可约的,由Perron-Frobenius定理可知,ρ(G)是单根,且有相应的正单位特征向量,记为X(G),称为G的距离Perron向量.
任取向量X=(x1,…,xn)T∈n(这里X可能是G的距离Perron向量,也可能不是),可将它的分量与G中的点一一对应,即分量xi对应顶点vi,则
若X是D(G)的相应于λ的特征向量,则对每一点u∈V(G),有
(1)
称式(1)为G在u点处的(λ,X)-特征方程.对于任意单位向量X∈n,由Rayleigh-Ritz定理[1],有
ρ(G)≥XTD(G)X
当X是G的距离Perron向量时,上式等号成立.对于G的子图H,记σG(H)为G的距离Perron向量中对应于V(H)的所有分量之和.
Pn表示n阶路,它是n阶连通图中距离谱半径最大的图[2].若一棵树,将其所有悬挂点删去后所得图是一条路,则称该树为毛毛虫图.显然,Pn自身也是毛毛虫图.
设V1⊂V(G),则G-V1表示将图G删去V1中的点以及相关联的所有边后所得到的图.若V1={u},则用G-u来代替G-{u}.对于E1⊂E(G),G-E1表示将图G删去E1中的边后所得到的图.相应地,用G-uv来代替G-{uv}.若E′是G的补图的一些边的集合,类似地,可以定义G+E′和G+uv.
距离矩阵的定义可以追溯到1841年Cayley 的论文[3],后来Graham[4]于1971年在距离矩阵的负特征值个数与数据通信系统中的寻址问题之间建立了一种关系,自此,距离谱的研究引起了众多图论学者的兴趣.与邻接矩阵相比,距离矩阵包含了图的更多信息,但同时也更加复杂,任意一条边的移动或者删除,都会给距离矩阵带来很大的变化,所以,研究难度较大.关于距离谱的综述见文献[5].
文献[6]研究了奇度点数固定的树集,刻画了距离谱半径最大的极图.受此启发,本文研究4度点数固定的树集,以及度至少为4的点数固定的树集,刻画了距离谱半径最大的极图.
2 关于图C(n,a,b)
现引入一类图C(n,a,b),并得到了一些性质.在考虑4度点数固定的树集时,距离谱半径最大的图就是此类图.
定义1设b≥a≥0,3(a+b)≤n-2,r=n-3a-3b-2,记图1所示的图为C(n,a,b).特别地,C(n,0,0)是路Pn.
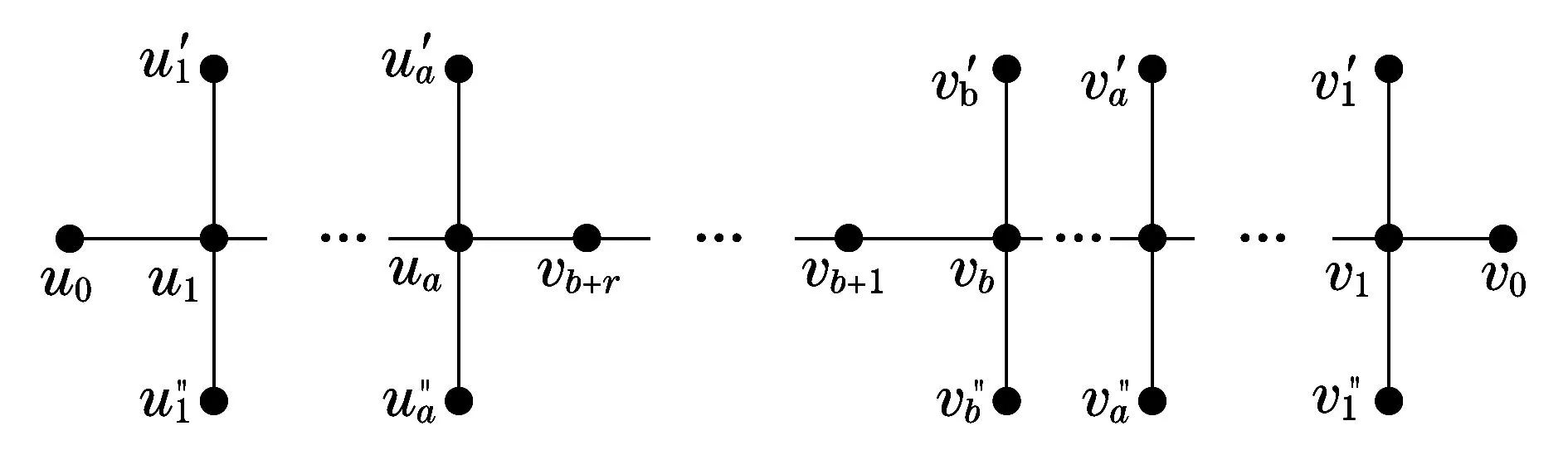
图1 C(n,a,b)Fig.1 C(n,a,b)
定义2设2≤Δ≤n-1,路Pn-Δ+1的1个端点连接Δ-1个悬挂点所得到的图记为Bn,Δ,如图2所示.
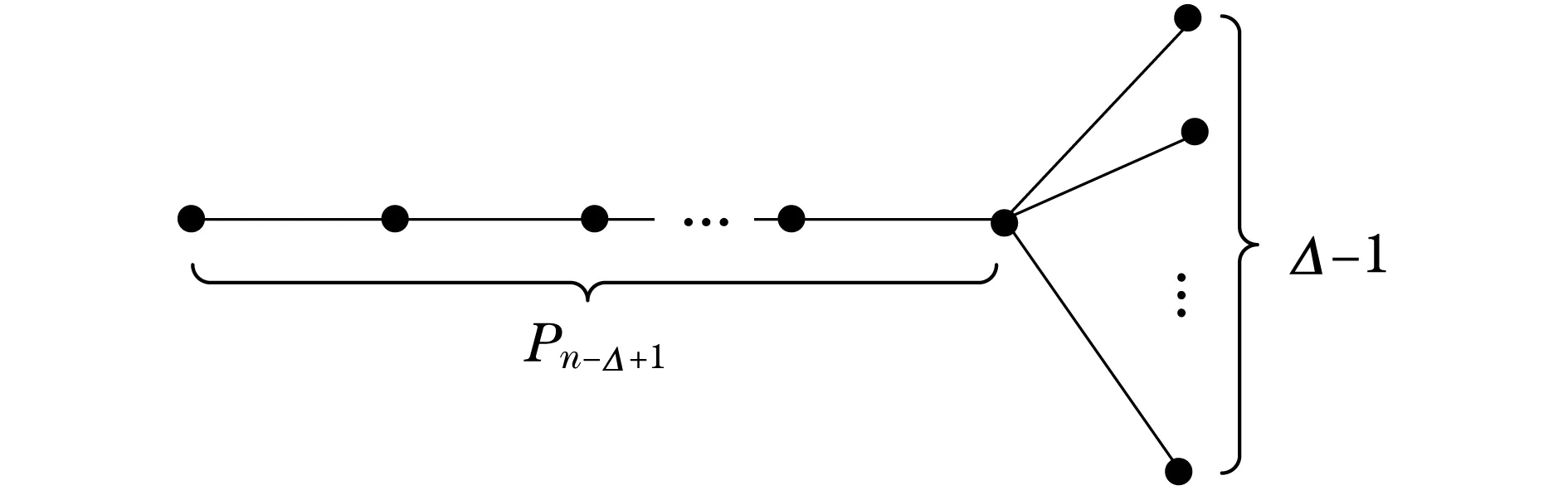
图2 Bn,ΔFig.2 Bn,Δ
引理1[7]设T是n(n≥4)阶树,Δ为最大度,则ρ(T)≤ρ(Bn,Δ),等式成立当且仅当T≅Bn,Δ.进一步,若Δ1>Δ2,则ρ(Bn,Δ1)<ρ(Bn,Δ2).
推论1设T是n(n≥5)阶树,最大度Δ≥4,则ρ(T)≤ρ(C(n,0,1)),等式成立当且仅当T≅C(n,0,1).
证明因为,Δ≥4,由引理1可知,ρ(T)≤ρ(Bn,Δ)≤ρ(Bn,4)=ρ(C(n,0,1)),等号成立当且仅当T=C(n,0,1),证毕.
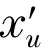
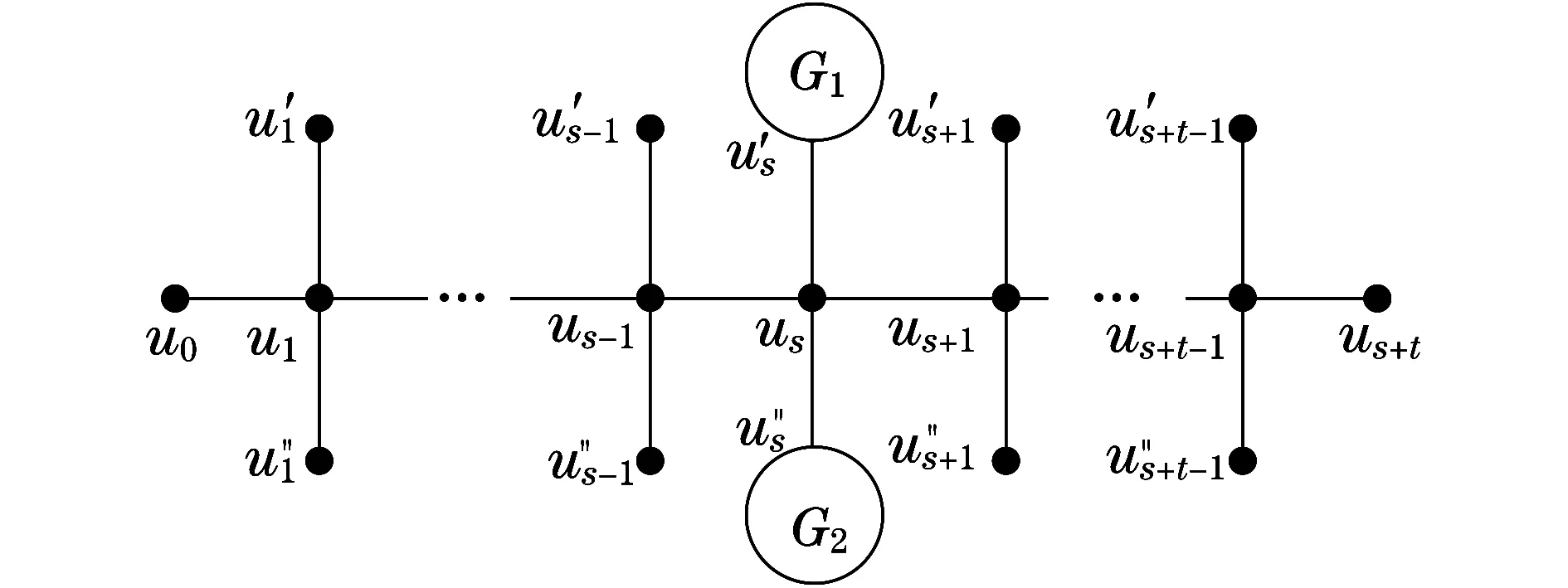
引理3[6]设T是树,u∈V(T),NT(u)={u1,…,uk},其中,k≥3,Ti为T-u的包含ui(1≤i≤k)的分支,w∈V(Tk),对于任意t=2,3,…,k-1,令T′=T-{uui:2≤i≤t}+{wui:2≤i≤t}.若σT(Tk)≤σT(T1),则ρ(T′)>ρ(T).
引理4[8]设G是n阶连通图,X=(x1,x2,…,xn)T是G的距离Perron向量,其分量xi与顶点vi对应.令vi-1vi,vivi+1是G的2条边,且vi-1vi,vivi+1中至少有1条是割边,若xi-1 引理5设图C(n,a,b)如图1所示,b≥a+2≥2, 3(a+b) a. 0 c. 0 d.xa+1-xa+r+1>xa+2-xa+r>…>xa+s-xa+t+1>0,其中,a+r+1=d-b,a+t+1=a+r+2-s. 图3 重新编号的C(n,a,b)Fig.3 Renumbered C(n,a,b) 现证明结论c. 断言1xp>xq+1. 当i=0时,由式(1)可知, (2) 在假设条件下,有xp≤xq+1成立. 于是,有yp-j≤yq+1+j(0≤j≤i-1)成立.因此, 即xp-i-xq+1+i≤xp-(i-1)-xq+i≤0,亦即xp-i≤xq+1+i也成立. 由数学归纳法可知,对于所有0≤i≤p,均有xp-i≤xq+1+i成立,从而有yp-i≤yq+1+i成立. 断言2x0>xd. 假设x0≤xd,现利用数学归纳法证xi≤xd-i(0≤i≤p). 当i≥1时,设xj≤xd-j(0≤j≤i-1)已成立.由引理2可知,yj≤yd-j(0≤j≤i-1),因此, ρ(T)(xi-xd-i)-ρ(T)(xi-1-xd-(i-1))= 于是,xi-xd-i≤xi-1-xd-(i-1)≤0,因此,xi≤xd-i(0≤i≤p).特别地,xp≤xq+1,矛盾,所以,x0>xd,断言2成立. 在断言2成立的基础上,类似地,可用数学归纳法得,0 现证明结论d. 现证明xa+s-i>xa+t+1+i(0≤i≤s-1). 当i=0时, ρ(T)(xa+s-xa+t+1)= 故xa+s>xa+t+1成立. 当1≤i≤s-1时,设xa+s-j>xa+t+1+j(0≤j≤i-1)已成立,即ya+s-j>ya+t+1+j(0≤j≤i-1),则 ρ(T)(xa+s-i-xa+t+1+i)-ρ(T)(xa+s-(i-1)-xa+t+i)= 于是, xa+s-i-xa+t+1+i>xa+s-(i-1)-xa+t+i>0 (3) 从而xa+s-i>xa+t+1+i成立.由数学归纳法可知,对于所有0≤i≤s-1,均有xa+s-i>xa+t+1+i成立.再由式(3)得结论d成立. 综上,引理5成立. 定理1设图C(n,a,b)如图1所示,b≥a+2≥2,3(a+b) ρ(C(n,a+1,b-1))>ρ(C(n,a,b)) 设T1,T2分别是T删去vb所得的含有点u0,v0的分支,当σT(T1)≤σT(T2)时,由引理3可知,结论显然成立.当σT(T1)>σT(T2)时,ρ(T)·(xvb-xvb-1)=σ(T2)-(σ(T1)+zb)<0,所以,xvb xvb (4) 由引理2可知, 所以 从而 (5) ρ(T′)-ρ(T)≥XT(D(T′)-D(T))X= 其中 现分两部分来证明w>0. a. 要证ρ(T′)>ρ(T),只需证w>0.由引理2和引理5的a可得 (6) 于是,由引理5的b及式(4)~(6)可得 r(3a+1)(xvb+r-xva+1)<2w+ 因此 (3a+1)r)(xvb+r-xvb) b. 由引理5的b可知,xvb+r-xvb>0,由Perron-Frobenius定理可知,不可约非负矩阵的谱半径大于等于最小行和,故要证w>0,只需证下面的命题. 对于任意0≤j≤a,有 若a≥1,则对于任意1≤j≤a,有 对于任意v∈R,有 对于任意0≤j≤b,有 对于任意1≤j≤b,有 综上,命题成立,从而ρ(T′)>ρ(T),定理1得证. 引入一种图的变换,得到距离谱半径的变化规律(引理6).进一步,研究4度点数固定的树集,以及度至少为4的点数固定的树集,刻画距离谱半径最大的极图(定理2和定理3). 图 因为,G1,G2中至少有1个非平凡分支,不妨设G1是非平凡分支.选1点v∈V(G1),满足 于是, 因此,断言3成立. 断言4σG(G4)≥σG(G3). 当i=1时 所以,xus-1-xus+1<0成立. 当2≤i≤s时,设xus-j-xus+j<0 (1≤j≤i-1)已成立,由引理2可知,ys-j-ys+j<0 (1≤j≤i-1),从而 所以,xus-i-xus+i 由数学归纳法可知,对于所有1≤i≤s,均有xus-i-xus+i<0成立. 证明设T*为满足引理7所给条件的距离谱半径最大的毛毛虫图,令t为T*中2度点的个数,按下面2种情形讨论. 情形1t≤1. 情形2t≥2. 综上,引理7成立. 证明当k=1时,由推论1可知结论成立.现考虑k≥2的情况,设T*为T(n,k)中距离谱半径最大的树. 断言5T*的最大偶度等于4. 否则,T*的最大偶度大于或等于6,不妨设dT*(u)=2t且t≥3.令NT*(u)={u1,…,u2t},Ti为T*-u的含有点ui(1≤i≤2t)的分支.不失一般性,设σT*(T2t)≤σT*(T1),令v为V(T2t)中的1个悬挂点,T=T*-uu2+vu2,T中4度点的个数仍为k,即T∈T(n,k),但由引理3可知,ρ(T)>ρ(T*),矛盾. 断言6T*的奇度点均为悬挂点. 现通过2种假设反正断言6. a. 假设T*的最大奇度大于或等于5,不妨设dT*(u)=2t+1且t≥2.令NT*(u)={u1,…,u2t+1},Ti为T*-u的含有点ui(1≤i≤2t+1)的分支.不失一般性,设σT*(T2t+1)≤σT*(T1),令v为V(T2t+1)中的1个悬挂点,T=T*-{uu2,uu3}+{vu2,vu3},注意到T∈T(n,k),但由引理3可知,ρ(T)>ρ(T*),矛盾. b. 假设T*的最大奇度等于3,不妨设dT*(u)=3.令NT*(u)={u1,u2,u3},Ti为T-u的含有点ui(i=1,2,3)的分支.不失一般性,设σT*(T3)≤σT*(T1),令v为V(T3)中的1个悬挂点,T=T*-uu2+vu2,T中4度点的个数仍为k,由引理3可知,ρ(T)>ρ(T*),矛盾. 综合a和b,断言6成立,从而T*中点的度只有3种情况:1,2或4. 断言7T*是毛毛虫图. 否则,设T×是将T*中所有悬挂点删去后所得的图,则至少存在1个点,在图T×中的度为3或4,将这些点构成的集合记为U.对于任意u∈U,仍有dT*(u)=4,令NT*(u)={u1,u2,u3,u4},dT*(ui)≥2,i=1,2,3.再令Ti为T*-u的含有点ui(i=1,2,3,4)的分支,则T*的2度点必全属于某个V(Ti),i∈{1,2,3,4}.若不然,存在度为2的2个点,1个在V(Ti)中,1个在V(Tj)中,i≠j,不妨设dT*(v1)=dT*(v3)=2,v1∈V(T1),v3∈V(T3),不失一般性,再设σT*(T3)≤σT*(T1).令T=T*-{uu2,uu4}+{v3u2,v3u4},则T∈T(n,k),但由引理3可知,ρ(T)>ρ(T*),矛盾.故不妨设T*的2度点全属于V(T1). 现分2种情形讨论. 情形1|UV(T1)|=1. 情形2|UV(T1)|>1. 设u′为UV(T1)中距离u最远的点,此时u′可看作情形1中的u,类似地,可推出矛盾. 综合情形1和2,断言7成立. 证明当k=1时,由推论1可知结论成立,以下考虑k≥2情况. 设T*是满足定理3条件的距离谱半径最大的树.假设Δ(T*)≥5,不妨设NT*(u)={u1,…,uΔ},令Ti为T*-u的含有点ui(i=1,…,Δ)的分支.不失一般性,设σT*(TΔ)≤σT*(T1),令T=T*-{uui:2≤i≤Δ-1}+{wui:2≤i≤Δ-1},其中,w为T*的属于V(TΔ)的悬挂点.易知T仍满足题设条件,由引理3可知,ρ(T)>ρ(T*),矛盾.所以,T*∈T(n,k),结合定理2,定理3得证. [1] HORN R A,JOHNSON C R. Matrix analysis[M].Cambridge:Cambridge University Press,1985. [3] CAYLEY A.A theorem in the geometry of position[J].The Cambridge Mathematical Journal,1841,2:267-271. [4] GRAHAM R L, POLLAK H O.On the addressing problem for loop switching[J].Bell System Technical Journal,1971,50(8):2495-2519. [5] AOUCHICHE M,HANSEN P.Distance spectra of graphs:a survey[J].Linear Algebra and its Applications,2014,458(2):301-386. [6] LIN H Y,ZHOU B.The distance spectral radius of graphs with given number of odd vertices[J].Electronic Journal of Linear Algebra,2016,31(1):286-305. [7] WANG Y N,ZHOU B.On distance spectral radius of graphs[J].Linear Algebra and its Applications,2013,438(8):3490-3503. [8] RUZIEH S N,POWERS D L.The distance spectrum of the pathPnand the first distance eigenvector of connected graphs[J].Linear Multilinear Algebra,1990,28(1/2):75-81. DistanceSpectralRadiusofTreeswithGivenNumberofVerticesofDegree4 WANG Yun,WUBaofeng (CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China) A graph transformation was introduced to show the effect of the distance spectral radius.Further,the set of trees with given number of vertices of degree 4 was studied,characterizing the extremal graph with the largest distance spectral radius.Finally,the more general class of graphs,namely,the set of trees with given number of vertices of degree at least 4 was discussed,and also its extremal graph was characterized. distancematrix;distancespectralradius;distancePerronvector;tree 1007-6735(2017)05-0409-07 10.13255/j.cnki.jusst.2017.05.001 2017-06-03 国家自然科学基金资助项目(11301340);上海自然科学基金资助项目(12ZR1420300);沪江基金资助项目(B14005) 汪云(1993-),女,硕士研究生.研究方向:代数图论.E-mail:751488437@qq.com 吴宝丰(1978-),男,讲师.研究方向:代数图论.E-mail:baufern@usst.edu.cn O157.5 A (编辑:石 瑛)


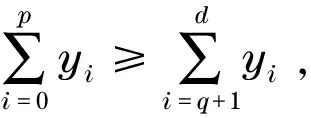




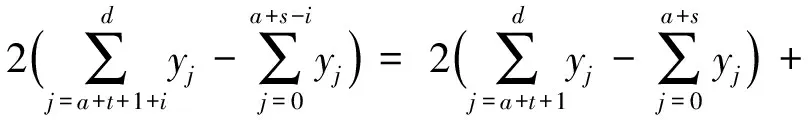
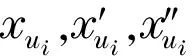





3 4度点数固定的树