三跨连续斜交T梁桥的动力特性研究

王荣霞，任腾腾，宋娃丽，张宇明

（1.河北工业大学 土木与交通学院，天津 300401；2.廊坊市交通勘察设计院，河北 廊坊 065000）

三跨连续斜交T梁桥的动力特性研究

王荣霞1，任腾腾1，宋娃丽1，张宇明2

（1.河北工业大学 土木与交通学院，天津 300401；2.廊坊市交通勘察设计院，河北 廊坊 065000）

为深入了解连续斜交梁桥的动力特性，以一座三跨连续斜交T梁桥为工程实例，建立了不同斜交角度的三跨连续斜交T梁桥的Midas Civil空间梁格模型，分析了斜交角的变化对结构的振型分布和自振频率的影响变化规律，并以斜交角作为影响因素，对现行《公路桥涵设计通用规范》中连续梁桥冲击系数计算采用的基频通用公式进行了修正.研究表明：三跨连续斜交T梁桥的竖弯振型分布在自然振型的不同阶数中，随着连续斜交梁桥斜交角度的增大，结构的弯扭效应变得更加明显，使得竖弯振型的分布也产生了变化；竖弯振型对应的自振频率均随斜交角的增加而增大，当斜交角度大于30°时，基频计算应计入斜交角影响；现场实桥动载试验表明本文提出的基频修正公式是比较合理的，对于此类结构的工程设计具有重要的参考价值.

三跨连续斜交T梁桥；斜交角；振型；自振频率

0 引言

近年来，随着我国桥梁建设的发展，为满足结构安全及线形的要求，修建了大量的斜桥.斜桥由于有斜交角的存在，其动力特性与正交桥会有明显的不同.对于连续斜交梁桥，在计算结构内力时，需要考虑冲击作用的影响而计算冲击系数.现行我国《公路桥涵设计通用规范》（JTG D60-2015）（以下简称“桥规”）在计算冲击系数时其公式中主要取决于结构的基频这一重要的动力特性参数.但是《桥规》中的基频计算公式并未对正桥和斜桥做出区分，这必然会对斜交角较大的连续梁桥的频率计算产生较大的影响，甚至导致与实际情况严重不符.因此很有必要对不同斜交角度的连续斜梁桥的动力特性进行深入研究.

目前学者们对斜桥动力特性的研究多集中于简支斜梁桥[1-7]，而对连续斜梁桥的动力特性的研究比较少[8-11].文献 [12]对于均匀的简单三跨连续梁的前三阶竖弯振型和相应的自振频率计算公式进行了详细的论述，但是，其计算公式却不适合于斜交连续梁桥，未考虑斜交角度的影响，这是与实际情况不符的.文献 [9-10]针对各跨的长度及截面完全相同的三跨均匀连续斜梁的自振频率推导出了超越方程，但是该方程公式计算复杂，且局限于单梁，不能完全符合真实桥梁的多梁式及不同横向联结方式等实际情况，因此对连续斜梁桥的动力特性需要更加深入系统的研究.

本文以某高速公路上的一座已建的三跨连续斜交T梁为依托工程，通过建立不同斜交角度该类结构的Midas空间梁格模型，计算出各模型的振型与相应的自振频率，分析其动力特性的变化规律，并根据这一规律将斜交角度作为变量，对现行《桥规》中所给出的连续梁桥冲击作用计算依据的基频公式进行修正，提出适合三跨连续斜交T梁桥的修正的基频计算公式.最后通过实桥动载试验验证了所提出公式的合理性.本文的研究结论可以为三跨连续斜梁桥的设计提供指导，具有很重要的理论和实用价值.

1 工程概况

该桥为标准跨径13 m的普通钢筋混凝土三等跨连续斜交T梁桥，设计荷载为公路Ⅰ级，斜交角为40°，行车道宽为15.75 m，上部主梁由11片T梁联结而成，其跨中横断面见图1所示.

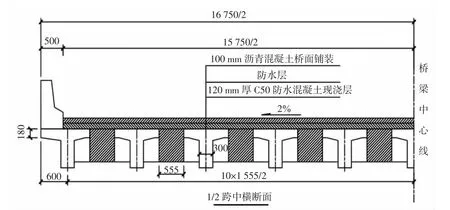
图1 主梁跨中横断面图Fig.1 Cross section drawing in the mid-span of main girder

2 Midas有限元梁格模型的建立

本文以实际工程为背景，应用Midas Civil软件中的梁格法建立了13种不同斜交角度的三跨连续斜梁桥的空间梁格模型，其斜交角度为0°～60°（间隔相差5°）.在模型中，纵梁的横向联结一部分为实际的横梁结构，另一部分为虚拟的横梁.虚拟横梁的布置方式有2种方法：第1种是当斜交角度小于15°时横梁平行于横隔板的方向，第2种是当斜交角度大于15°时横梁垂直于主梁的方向.全桥上部结构梁格模型如图2所示.

图2 斜桥的梁格模型Fig.2 Grillage models of skew bridge

3 有限元计算结果与分析

由文献 [11]，对于《桥规》中计算连续梁桥的冲击系数时所需的频率值应该是与竖弯振型相对应的自振频率值，因此竖弯振型及其相应的自振频率是设计者更加关注的.在结构设计时，计算主梁跨中正弯矩及剪力效应时的冲击系数按第1阶竖弯自振频率（基频）计算，而计算负弯矩效应时冲击系数应按第3阶竖弯自振频率计算.表1列出了不同斜交角度的三跨连续斜交T梁桥有限元模型所计算的前7阶自然振型图，其中包含了前3阶竖弯振型.

表1 不同斜交角度下桥梁模型的前7阶自然振型图Tab.1 The first seven natural mode shapes of skew bridge models with different skew angles

表1中，当斜交角为0°时，三跨连续梁桥模型的前3阶竖弯振型图与文献 [12]的理论振型基本一致.且从表1中可看出，当斜交角度为0°（即正桥）时竖弯振型的前3阶分布在自然振型的1、3、5阶；当斜交角度为5°～10°时，竖弯振型的前3阶分布在自然振型的1、3、6阶；当斜交角度为15°～60°时，竖弯振型的前3阶分布在自然振型的1、3、7阶.由此可见，随着连续斜交梁桥的斜交角度的增大，结构的弯扭效应更加明显，使得竖弯振型的分布也产生了变化，为保证结构设计的安全，需要在计算时考虑斜交角的影响.

针对不同斜交角度的三跨连续斜交T梁桥结构系列模型，分别进行了前3阶竖弯自振频率fs1、fs2、fs3的计算，并与正桥模型的前3阶自振频率进行了对比，结果见表2.

综合表1和表2结果可以看出，三跨连续正交梁桥模型的前3阶竖弯振型及其自振频率值分别与文献[12]中连续梁弯曲固有振动的竖弯振型及频率的理论解非常接近，两者自振频率的相对误差不大于5%，在允许的范围内.由于各模型除了斜交角度不同并无其他区别，因此可认为本文建立的所有模型是基本合理的，计算结果是真实可靠的，可用来进行更深入的分析.

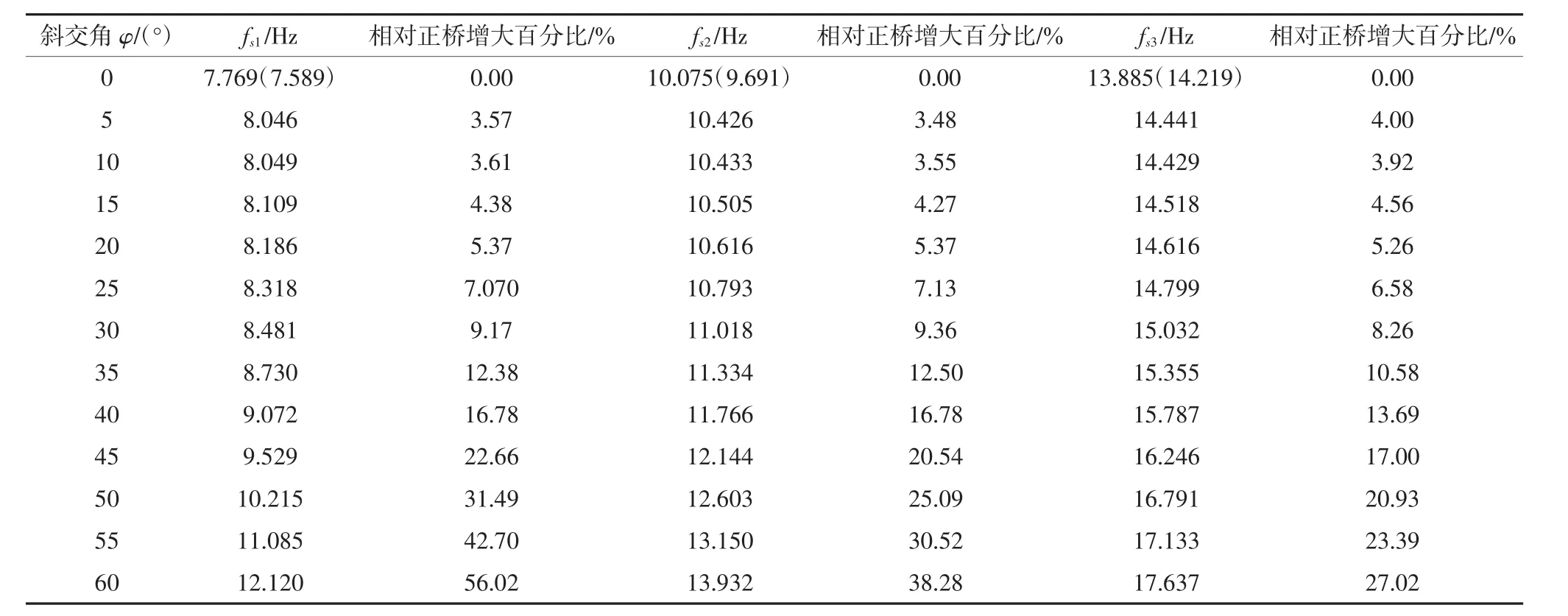
表2 前三阶竖弯振型相应的自振频率计算结果Tab.2 The natural vibration frequencies of the first three order vertical bending modes

应用最小二乘法对表2第1阶竖弯自振频率fs1和第3阶竖弯自振频率fs3进行拟合，得到自振频率fs1和fs3随着斜交角变化的拟合曲线，分別如图3和图4所示.

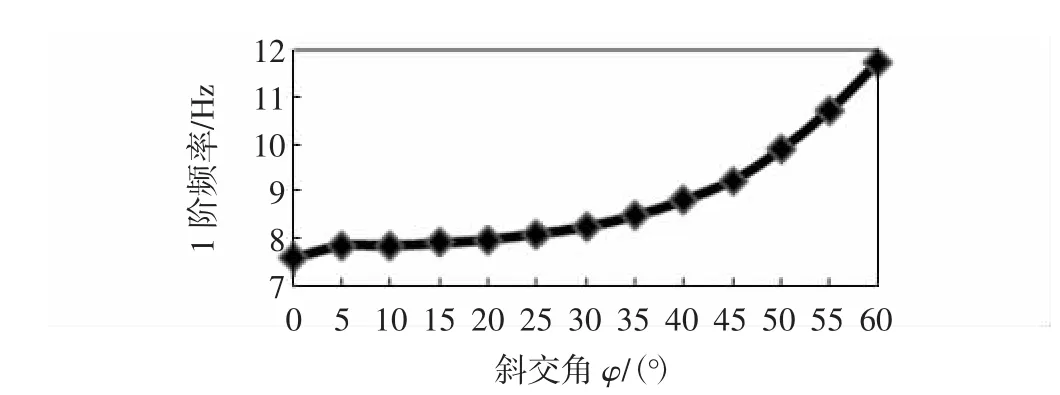
图3 基频fs1拟合曲线Fig.3 Fitting curve of the fundamental frequency fs1

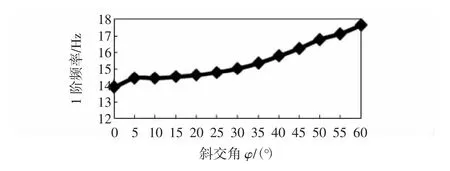
图4 基频fs3拟合曲线Fig.4 Fitting curve of the fundamental frequency fs3

由图3和图4中的曲线可知，结构的各阶自振频率数值均会随着斜交角度的增加而增大，在斜交角小于30°时，斜桥的基频值与正桥基本相近，设计时可以按正桥公式计算；但当斜交角大于30°时，则应按斜桥进行基频的计算，否则在设计中将会产生较大的误差.如斜交角为45°的斜桥基频比正桥增大22.66%，若按《桥规》公式计算冲击系数将比正桥增大10.42%，需要引起设计者的注意.

4 三跨连续斜交T梁桥的基频修正

为科学指导三跨斜交连续T梁桥的工程设计，考虑斜交角的影响，并根据表2中数据对《桥规》中冲击系数所采用的基频计算公式进行以下修正：

1）计算三跨连续梁桥冲击力引起的正弯矩效应及剪力效应时，基频fx1的计算公式

式中，f（φ）1为考虑斜交角φ影响的正弯矩及剪力效应计算采用的基频修正系数.

2）计算三跨连续梁桥冲击力引起的负弯矩效应时，基频fx2的计算公式

式中，f（φ）2为考虑斜交角φ影响的负弯矩效应计算采用的基频修正系数.

由此，当三跨连续梁桥斜交角小于30°时，式（2）、式（3）和式（6）、式（7）可作为基频计算的参考；但当三跨连续梁桥斜交角大于30°时，工程设计应按式（4）和式（8）进行斜桥基频的精确计算.

5 实桥现场动载试验

对某高速公路一座三跨连续斜交T梁桥（斜交角为40°）进行现场动载实验.现场采用TST5926E无线环境激励实验模态采集分析系统.试验测点选取边跨跨中和中跨跨中位置，本次试验只测得该桥的基频fx1.

本次试验工况包括：工况1：试验车以60 km/h车速匀速跑过该桥；工况2：试验车以70 km/h车速匀速跑过该桥；工况3：2辆试验车分别在中跨跨中进行跳车试验.

限于篇幅，文中只给出工况1在中跨跨中采集器得到的时域信号波形图和对应的频谱分析图，如图5和图6所示.最终各工况的基频实测结果如下：

工况1：中跨跨中为9.86 Hz，边跨跨中为9.77 Hz，代入《桥规》公式计算冲击系数分别为0.389和0.387.

工况2：中跨跨中为9.42 Hz，边跨跨中为9.96 Hz，代入《桥规》公式计算冲击系数分别为0.381和0.390.

工况3：中跨跨中为9.84 Hz，代入《桥规》公式计算冲击系数为0.388.

由修正公式（1）和公式（4）计算的基频值为9.03 Hz，带入《桥规》公式计算冲击系数为0.373.

经计算比较，由以上各工况实测基频计算的冲击系数，与由拟合公式得到基频值计算的冲击系数相差最大为4.47%，说明本文提出的公式结果较为合理，可以作为斜交三跨连续梁桥基频理论计算的参考依据.

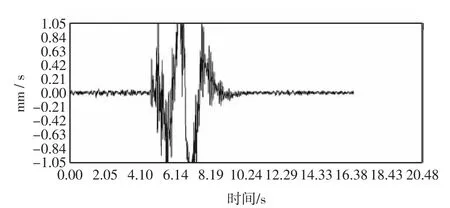
图5 中跨跨中的时域信号波形图Fig.5 Time domain signal waveform chart in mid-span of central span

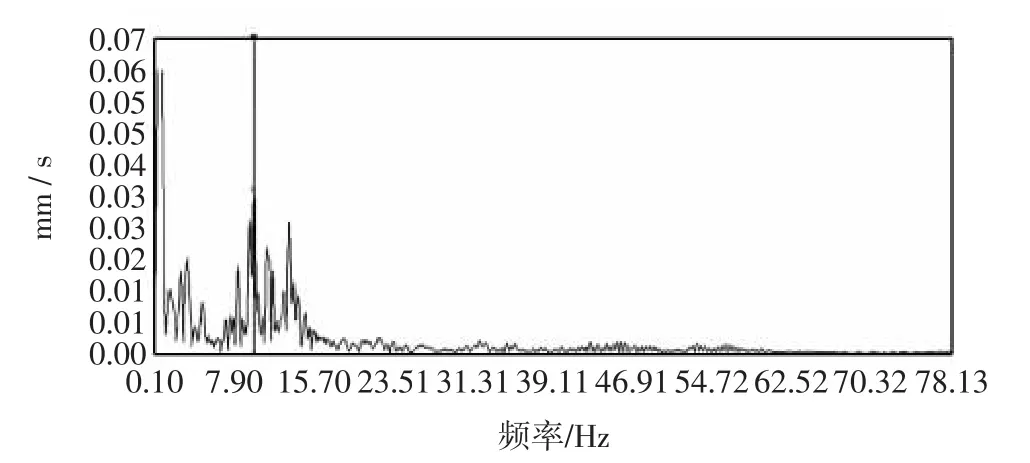
图6 中跨跨中的信号频谱分析图Fig.6 Signal frequency spectrum analysis in mid-span of central span

6 结论

1）由三跨连续斜交T梁桥模型的前7阶振型图可以看出，当连续斜交梁桥的斜交角度较大时，结构的弯扭效应更加明显，使得竖弯振型的分布也产生了变化.

2）三跨连续斜交T梁桥各阶自振频率值均随着斜交度的增加而增大，当斜交角从0°变化到5°时，由于斜交角的存在，频率值有一个小突变，在5°～30°区间，增加的幅度缓慢，斜交角度大于30°以后频率随斜交角增大的幅度逐渐加大.

3）在斜交角小于30°时，斜桥的基频值与正桥相近，基频计算可以按正桥考虑；当斜交角大于30°时，应按斜桥进行具体计算，否则将会产生较大的误差.

4）通过一座三跨连续斜交T梁桥的现场动载试验，验证了本文提出的计算连续梁冲击系数采用的基频修正公式是比较合理的，可以用于指导此类结构的工程设计.

[1] 张等.不同斜交角度简支T形梁桥基频计算与试验[J].湖南交通科技，2016，42（1）：74-77.

[2] 刘小燕，袁龙文，何志军.斜交空心板桥基频计算与实验[J].中外公路，2012，32（3）：189-191.

[3] 夏樟华，宗周红.三跨斜交T梁动力特性分析[J].振动与冲击，2007，26（4）：147-150.

[4] 夏桂云，俞茂宏，李传习，等.斜桥动力特性[J].交通运输工程学报，2009，9（4）：15-21.

[5] Maleki S.Free vibration of skewed bridge[J].Journal of Vibration and Control，2001，7：935-952.

[6] Afshin Kalantari，Mohsen Amjadian.An approximate method for dynamic analysis of skewed highway bridges with continuous rigid deck[J].Engineering Structures，2010，32（9）：2850-2860.

[7] Mohseni Iman，Abdul Khalim Abdul Rashid，Junsunk Kang.A simplified method to estimate the fundation frequency of skew continuous multicell boxgirder bridge[J].Latin American Journal of Solids and Structures，2014，11：649-658.

[8] 何旭辉，盛兴旺，陈政清.高速铁路PC斜交箱梁桥振动特性模型试验研究[J].铁道学报，2002，24（5）：89-92.

[9] 夏桂云，李传习，张建仁.多跨连续斜桥动力特性分析[J].重庆大学学报，2011，34（8）：121-127.

[10]何朝晖，廖林清.多跨连续梁的振动[J].重庆工业管理学院学报，1995，9（4）：68-76.

[11]袁向荣.基于连续梁振动分析的桥梁冲击系数研究[J].四川建筑科学研究，2013，39（4）：190-194.

[12]宋一凡.公路桥梁动力学[M].北京：人民交通出版社，2000.

[13]王光远.建筑结构的振动[M].北京：科学出版社，1978.

A study on dynamic characteristics of continuous T-beam bridge

WANG Rongxia1,REN Tengteng1,SONG Wali1,ZHANG Yuming2

（1.School of Civil Engineering and Transportation,Hebei University of Technology,Tianjin 300401,China;2.Langfang Designing Institute of Traffic Investigation,Hebei Langfang 065000,China）

Spatial beam lattice model of a three-span continuous skew T-beam bridge is built in Midas Civil to provide a deep understanding toward the dynamic characteristics of such structure,and the changing regulation of natural vibration frequency and vibration mode with different skew angles is analyzed.Based on current codes,a modified calculation formula of fundamental frequency is put forward to consider the effect of skew angle structure.The study shows that for threespan continuous skew bridge,the vertical bending vibration modes are distributed in different orders of natural vibration modes.With the increase of the skew angle of the continuous skew girder bridge,the affection of bending and torsion on the structure is more obvious,and the distribution of the vertical bending modes in the natural vibration modes is also changed.The vertical bending vibration frequency increases with the skew angle.When skew angle is greater than 30 degrees,the effect of skew angle on the calculation value of frequency should be considered.The rationality of the formula proved by this paper is verified by the field bridge dynamic loading test,and it will provide important references for the engineering design of such structure.

three span skew continuous T-beam bridge;skew angle;vibration mode;natural frequency

U441.3

A

1007-2373（2017） 05-0068-06

10.14081/j.cnki.hgdxb.2017.05.012

2017-02-23

天津市交通运输委员会科技发展计划（2016A-07）；廊坊市科技支撑计划（2016013073，2017013003）

王荣霞（1971-），女，副教授，博士，wangrongxia2000@126.com.

[责任编辑 杨 屹]