正整数积性子半群中的计数问题
朱晓杰,姚维利
正整数积性子半群中的计数问题
朱晓杰,姚维利
(上海大学理学院,上海200444)
设S和S′为正整数集N满足特定条件的乘子半群的最小生成元系,记〈A〉为由A生和NS∪S′(x)联系的计算公式.利用该公式以及多变量的数学归纳法推出了由有限递增素数列{pi}生成的子半群中元素个数的渐近估计式.
M¨obius函数;整数子半群;素数;数论函数;渐近估计
令µ:N → {−1,0,1}表示M¨obius函数.当n=p1p2...pk时µ(n)=(−1)k,其中各pi为互不相同的素数;而当n=1时µ(1)=1;其他情况下µ(n)=0.另外,用符号[x]表示不超过x的最大整数.关于M¨obius函数的经典结果中有如下两个等式[1]:

和

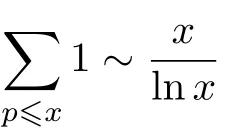
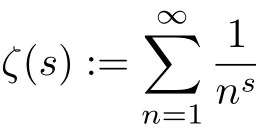
在直线Re(s)=1上只有s=1一个极点等价.与之相关的另一个估计式

则与Riemann猜想等价[3-4].Beurling[5]使用初等方法将式(2)推广到由素数生成的N乘子半群上:

式中,P为由一些素数构成的集合.如果A⊆N,则<A>表示由A生成的乘子半群(含有1).
本工作将得到一个使用M¨obius函数表述的一般的子半群上的计数公式,而式(3)则为该公式的特例.这里所说的子半群是指正整数集N的含有单位元1的乘子半群,称S⊆N为子半群D⊆N的生成元系,

在此基础上如果对任意的s∈S有〈S{s}〉/=〈S〉,则称S为D的最小生成元系.另外,使用记号
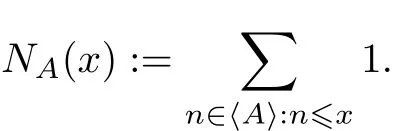
定理1 设S为N的一个乘子半群的一个最小生成元系,S′为一个素数组成的集合,S中任一元素均和S′中元素互素,x为实数,x>1,则
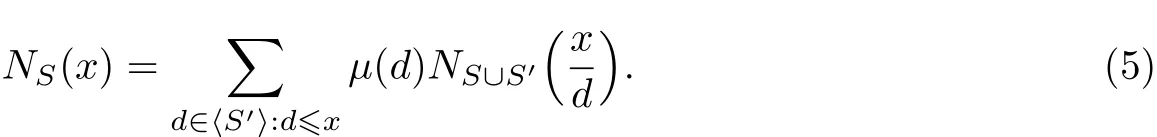
在定理1中选取S=∅,则得到

再进一步选取 S′={2,3,5,7,···} 为全体素数集,此时 〈S′〉=N 以及 NS′(x/d)=就得到式(1).如果选取S为某些素数构成的集合,而S′为与S互补的素数集,即S∪S′为全体素数集 {2,3,5,7,···},得到

由此可以推出式(3),而这在文献[5]中是直接证明的.
利用定理1,可得到如下两个推论.
推论1在定理1的符号下,若S′={p},p/∈S为一个素数,则下式成立:
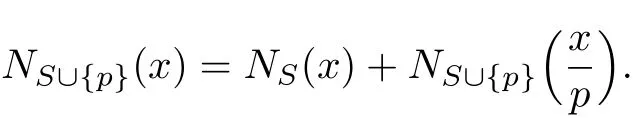
推论2在定理1的符号下,设s≥0为自然数.如果S′={p1,p2,···,ps},诸pi/∈S为互异素数,则下式成立:
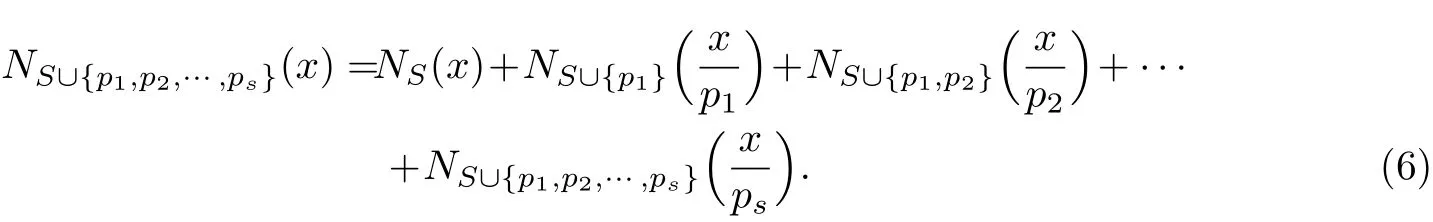
这些公式给出了一种估计NS(x)阶的递归方法.为了叙述定理2,需引入一些记号.设{pi}为无限递增素数列,数列{cn|n≥1}为

当n≥2时定义数列为


数列{dn|n≥1}由递推公式

给出.数列{en|n≥1}则由递推公式

给出.
定理2 设正整数x≥3,{pi}为无限递增素数列,t为任意正整数,数列{cn},{dn},{en}分别按式(7),(9)以及(10)定义,有

式中,et(lnx)t−1≤ ft(x)≤ dt(lnx)t−1.
目前,对于NS(x)阶的研究主要集中在当S是素数构成的集合时[6-7].
1 定理1的证明
定理1的证明使用符号δ来表示特征函数,当x∈A时δA(x)=1,而当x/∈A时δA(x)=0.证明当n ∈ 〈S ∪S′〉时

分两种情况讨论:n∈〈S〉以及n/∈〈S〉.当n∈〈S〉时δ〈S〉(n)=1.由于S及S′中元素互素,因此 〈S〉∩ 〈S′〉={1}. 故而对于d∈ N,d∈ 〈S′〉且 d|n当且仅当 d=1,因此式(12)成立.当n/∈〈S〉时由生成半群的定义(4)可以得到分解式

式中,k≥0,m≥0,αi≥1,βi≥1均为自然数,si∈S,pi∈S′,诸si各不相同,诸pi也各不相同.因为S及S′为相互间元素互素的最简生成元系,所以S∪S′也是最小生成元系,进一步分解式(13)中pi部分在不计次序的意义下唯一.另外,由于n∈/〈S〉故而m≥1.在这种情况下,对于d∈N有d∈〈S′〉且d|n当且仅当d|,故

上式中第2步的推导可参考任何一本初等数论教材[8].另外,当n/∈〈S〉时δ〈S〉(n)=0,这就证明了式(12)成立.
在式(12)两边对所有n∈〈S∪S′〉:n≤x求和得到
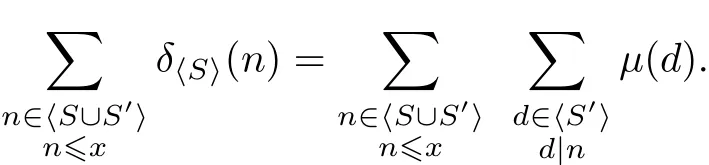
上式左边即为NS(x),计算上式右边得到

为了在式(14)右边第2个求和号内使用变量替换n=dn′,注意到若d∈〈S′〉,n′∈N,则dn′∈ 〈S ∪ S′〉当且仅当 n′∈ 〈S ∪S′〉. 于是

推论1的证明 推论1可立即由定理1推出,只要注意到此时

并利用M¨obius函数的定义即可.
推论2的证明 推论2可通过推论1以及数学归纳法证明.
2 定理2的证明
在定理2之前数列{an}的定义中涉及一个解析函数的最大值,此最大值的存在性由如下引理保证.
引理1 设t≥2为正整数,以及

引理1的证明 对于t=2结论显然成立,故下面设t≥3.对g(z)中2个二项式展开得
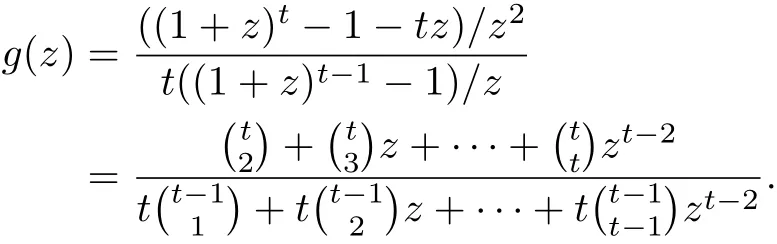
g(z)为有理函数,故g(z)的所有极点即为其分母的所有零点.而

的全体零点是方程(1+z)t−1=1的非零解,即

复平面上的点z=0到这些零点距离的最小值为

利用不等式

并且注意到t≥3就得到
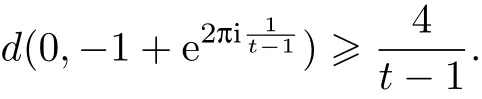
在定理2的证明中需要使用关于变量t及x的二元数学归纳法[9].
引理2 设t0及x0为整数,P(t,x)是关于整数变量t≥t0及x≥x0的命题,如果
(1)对于t=t0且x≥x0,命题P(t,x)成立,
(2)对于t≥t0且x=x0,命题P(t,x)成立,
(3)对一切满足 t0≤ t′≤ t,x0≤ x′≤ x 以及 t′+x′< t+x 的 t′,x′,命题 P(t′,x′)成立,则命题P(t,x)成立,那么对于一切t≥t0及x≥x0,命题P(t,x)成立.
定理2的证明 证明关于正整数变量t和x的不等式

使用关于变量t及x的二元数学归纳法(引理2)来证明.

所以有

步骤2 在条件t≥1,x=3下证明,即需证明

观察到

就能得到

容易验证,在每种情况下ft(3)均为正数,而et≤0,就得出了式(19)左边的不等式.对t使用归纳法来证明式(19)右边的不等式.当t=1时已在步骤1中证明.假设命题变量为t−1,t≥2时式(19)成立,由此来证明当命题变量取为t时式(19)成立.对于t≥3的情况,如果p1≥5,则由数列{dn}定义,归纳假设以及显然的不等式
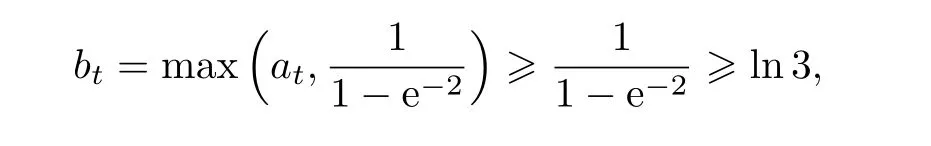
可以得到

如果p1=3或p1=2且p2≥5,则有类似的推导:

而如果p1=2且p2=3,推导类似.对于t=2的情况,若p1≥5,则仍可使用式(20)中的方法推导;若p1=3或p1=2且p2≥5,则仍可使用式(21)中的方法推导;若p1=2且p2=3,则有

这就完成了对t的归纳法,从而完成了步骤2的证明.
步骤3 假设对一切满足 1≤ t′≤ t,3≤ x′≤ x以及t′+x′< t+x的t′,x′,式 (16)成立,证明对于t和x也成立.t=1的情况前面已经证明过,因此设t≥2.在推论1中令S={p1,p2,···,pt−1} 以及 p=pt,然后两边除以 (lnx)t可以得到
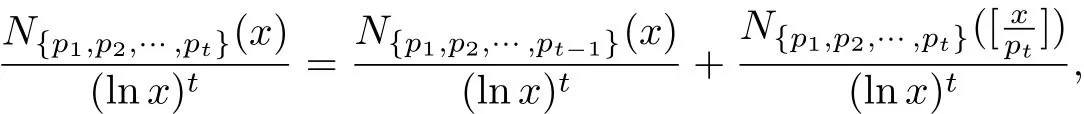
上式右边第2项使用了公式



证明
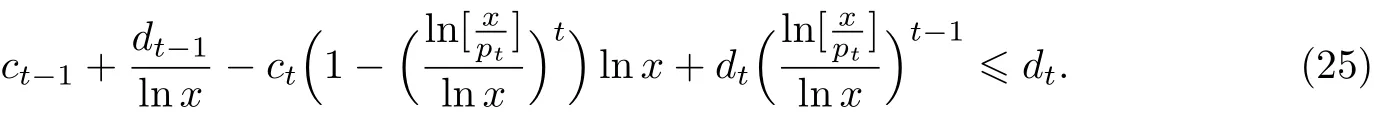
由式(24)及(25)就能证明式(16)右边的不等式对t和x成立.观察到式(25)等价于

分x≥有
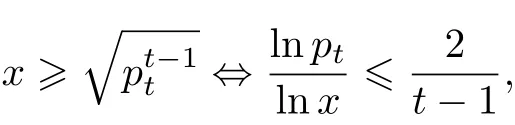
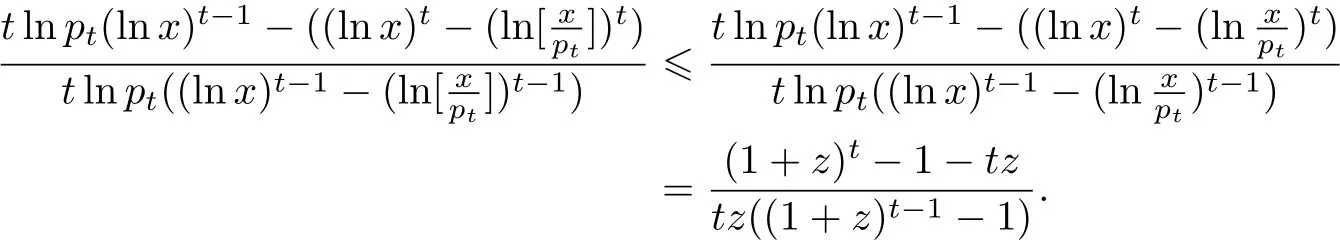
由上式以及引理1知

式(26)中dt−1的系数为


这就在x≥的差别.由式(22)知

由此可推出此时t≥3.证明和式(26)等价的如下不等式:
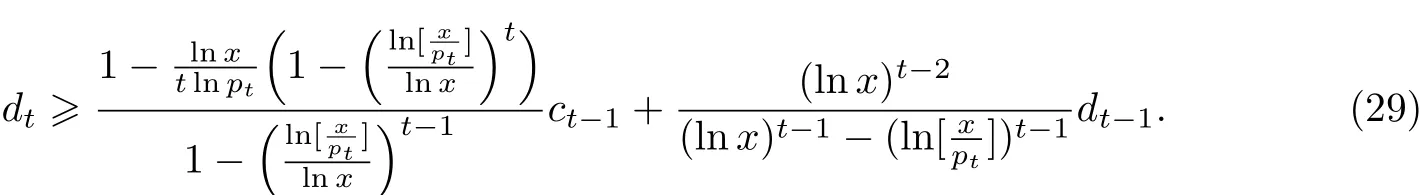

结合推出

从而
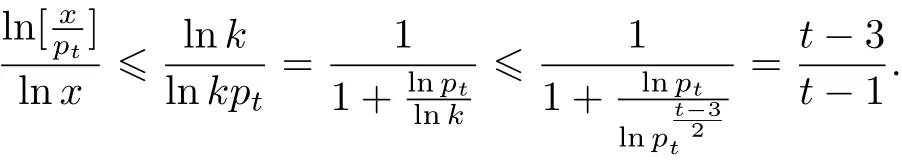

注意到式(28)中的推导对于情况也成立.结合式(28),(30)以及{dn}的定义(式(9))就能推出式(29).这样就证明了式(16)右边的不等式对t和x成立.下面证明式(16)左边的不等式对t和x成立.由式(23)以及归纳假设知
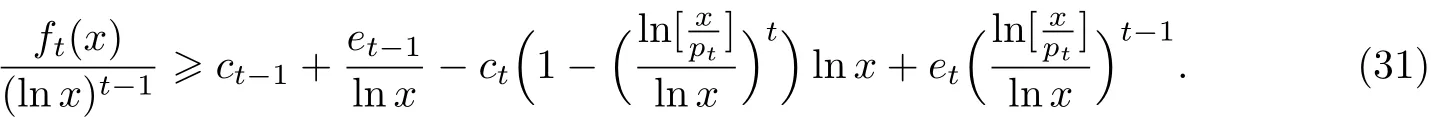
下面证明
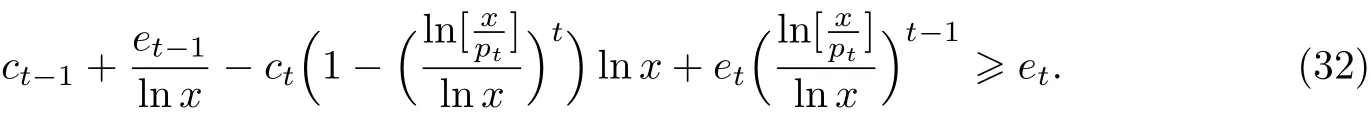
由式(31)以及(32)就能证明式(16)左边的不等式对t和x成立.可以看到,这和式(25)的证明是类似的,即首先写出式(32)的等价形式
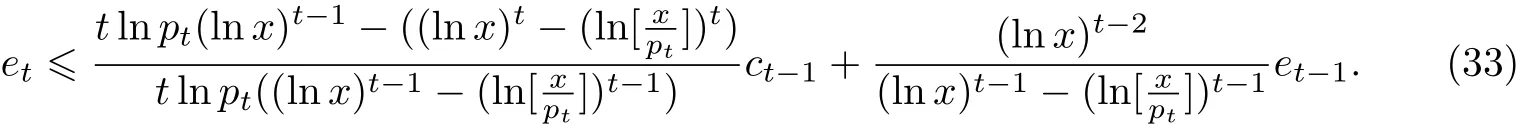

其中c=0,1或2.故

因为x<3pt≤,所以式(34)中(lnx)t−1的系数

另外,当x≥5时容易验证(注意t≥2以及c≤2)

当x=4时c=1,故上式也成立.由于已经就4≤x<3pt证明了式(16),而x=3的情况已经在步骤2中证明,因而对于x<3pt,式(16)均成立.这就完成了归纳法的步骤3,从而完成了整个证明.
[1]ApOSTOL T M.Introduction to analytic number theory[M].Berlin:Springer-Verlag,1976.
[2]LANDAU E.¨Uber den zusammenhang einiger neuer s¨atze der analytischen zahlentheorie[C]//Wiener Sitzungsberichte,Math Klasse.1906:115.
[3]ALkAN E,G¨ORAL H.On sums over the M¨obius function and discrepancy of fractions[J].Journal of Number Theory,2013,133:2217-2239.
[4]DAvENpORT H.Multiplicative number theory[M].3rd ed.Berlin:Springer-Verlag,2000.
[5]BEURLING A.Analyse de la loi asymptotique de la distribution des nombres premiers g´en´eralis´es.Ⅰ[J].Acta Mathematica,1937,68(1):255-291.
[6]TAO T.A remark on partial sums involving the M¨obius function[J].Bulletin of the Australian Mathematical Society,2010,81:343-349.
[7]ZHANG W B.A generalization of Hal´asz theorem to Beurling’s generalized integers and its application[J].Illinois Journal of Mathematics,1987,31:645-664.
[8]潘承洞,潘承彪.初等数论[M].3版.北京:北京大学出版社,2013.
[9]柯斯特利金.代数学引论(第一卷)[M].2版.北京:高等教育出版社,2006.
Counting problem in multiplicative subsemigroups of positive integers
ZHU Xiaojie, YAO Weili
(College of Sciences,Shanghai University,Shanghai 200444,China)
Let S and S′be minimal systems of generators of specif i c subsemigroups of positive integers N.If,then〈A〉is the subsemigroup generated by A.Let NA(x):=tained via elementary methods of changing summation order.With this formula and induction on several variables,an asymptotic estimation of the number of element in a subsemigroup generated by a f i nite set of primes is obtained.
M¨obius function;subsemigroups of integers;primes;arithmetical function;asymptotic estimation
O 156.4
A
1007-2861(2017)05-0722-10
10.12066/j.issn.1007-2861.1749
2015-11-13
国家自然科学基金资助项目(11301325)
姚维利(1977—),女,副教授,博士,研究方向为解析数论.E-mail:yaoweili@shu.edu.cn

