预应力配束对连续箱梁内力影响分析

姜 磊

（北京国道通公路设计研究院股份有限公司，北京100053）

1 概述

预应力连续箱梁结构形式在市政及公路桥梁建设中屡见不鲜，影响其结构设计的因素有很多，但设计的最终是结构抗力大于结构内力。从抗力和内力两个方向追溯，影响内力的因素主要有作用效应、跨径布置等，影响抗力的因素主要有配筋、配束、截面尺寸和材料特性等，其中两项同时影响的因素有配束、截面尺寸和材料特性等。但在工程设计中一些参数受到限制已经固定，例如活载类型、二期恒载、材料特性、结构高度以及跨径，为了满足结构要求，只能从配束方式得以解决，因此有效的预应力配束对工程设计有着重要的影响。

在实际工程中，考虑到预应力损失、温度与收缩徐变的影响，连续箱梁结构一般控制在一联150 m以下，跨径一般为2跨、3跨、4跨、5跨，本次分析便从这4种跨径形式出发，分别对其进行计算比较分析，得出结论以指导设计。

2 计算分析主要内容

本次计算分析内容主要有两项：

a）不同分跨对结构内力的影响，主要对比结构各跨跨中及支点弯矩，因为连续梁内的预应力束筋的布置通常以实际荷载作用下的弯矩图形的线型变化为参考，即吻合束线型。

b）各跨跨中预应力束重心位置对结构内力的影响，主要对比结构各跨跨中及支点弯矩。

3 计算模型及计算程序的选取

为了分析结果具有可比性，拟定结构的跨径统一为30 m，分别为：

a）结构一2×30 m；

b）结构二3×30 m；

c）结构三4×30 m；

d）结构四5×30 m。

模型采用平面杆系单元，支承为铰接，截面抗弯刚度EI=1.26×1011m2,自重G=95 kN/m，计算程序采用结构力学求解器（SM Solver）。计算模型图见图1。

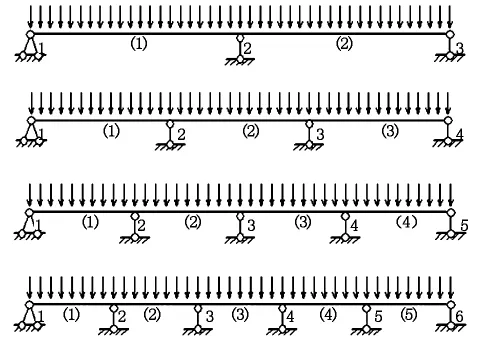
图1 2～5跨计算模型图

各跨跨中梁底预应力钢束重心位置变化采用等代作用效应，即通过配重调整模拟。当预应力钢束重心下移，相当于自重卸荷；预应力钢束重心上移动，相当于自重加荷。

4 计算结果分析

4.1 恒载作用下内力（弯矩）结果对比

通过计算得出4种分跨结构自重下（不考虑预应力）的内力结果，对其进行汇总，比较每种分跨结构对箱梁内力的影响。结果见图2和表1。

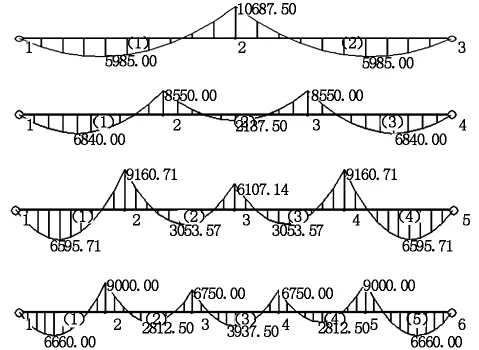
图2 2～5跨自重内力结果

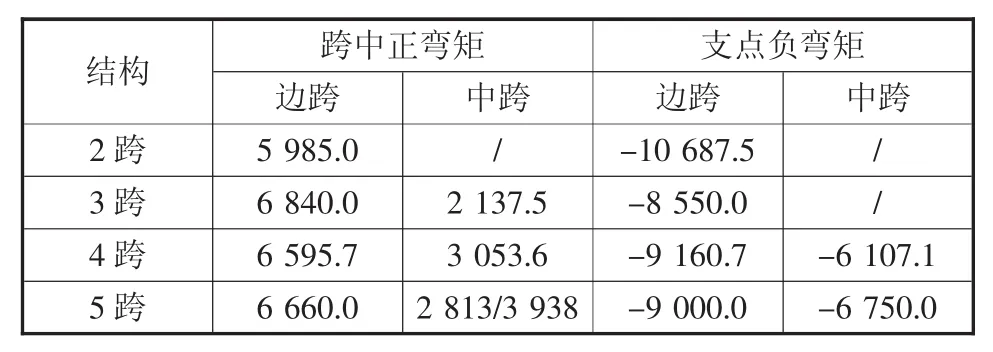
表1 2～5跨自重内力汇总表kN·m

从表1可以看出，各分跨结构支点负弯矩绝对值和跨中正弯矩值绝对值均为边跨大于中跨，且全桥负弯矩绝对值大于正弯矩值绝对值,即全桥由支点负弯矩控制设计。3跨结构支点负弯矩绝对值小于相邻偶数跨结构支点负弯矩绝对值，即奇数分跨较偶数分跨合理。

4.2 跨中梁底预应力重心位置调整内力结果对比

通过分别对各分跨结构边跨、中跨（对称调整自重20%）配重的调整模拟预应力重心位置的变化来研究结构正负弯矩的变化规律。梁底钢束重心下移，自重减轻20%，梁底钢束重心上移，自重增加20%。

4.2.1 2跨结构

计算结果见表2。

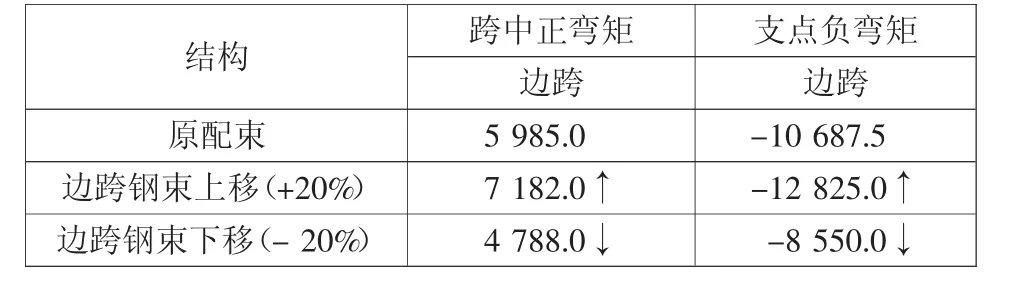
表2 2跨结构调束内力汇总表kN·m

从表2可以看出，边跨跨中梁底钢束上移，正、负弯矩均增大；梁底钢束下移，正、负弯矩均减小。

合理配束方式应为跨中梁底钢束重心尽量压低。

4.2.2 3跨结构

计算结果见表3。

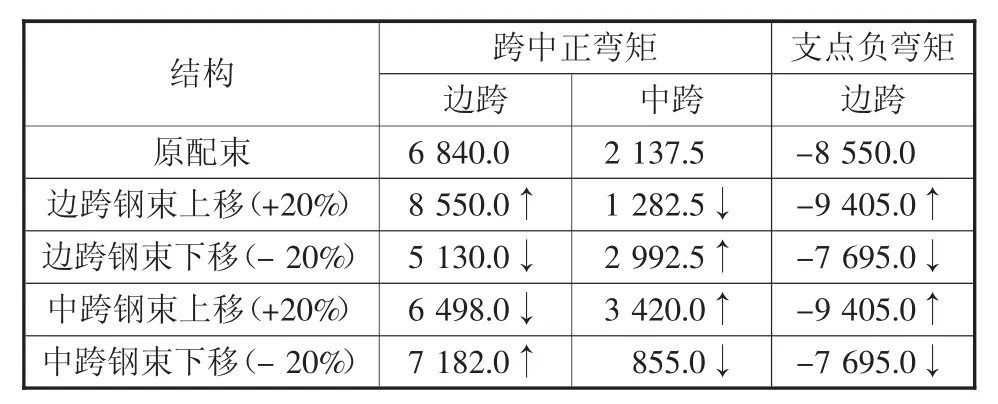
表3 3跨结构调束内力汇总表kN·m

从表3可以看出：

a）对于跨中正弯矩 钢束上移，本跨跨中正弯矩增大，邻跨正弯矩减小，下移作用相反。

b）对于支点负弯矩 边跨跨中、中跨跨中梁底钢束上移，负弯矩均增大；梁底钢束下移，负弯矩均减小。

因此，配束方式应为3跨跨中钢束尽量压低，当中跨跨中梁顶出现拉应力时，可将中跨跨中梁底钢束适当上移以加大中跨跨中正弯矩。

4.2.3 4跨结构

计算结果见表4。

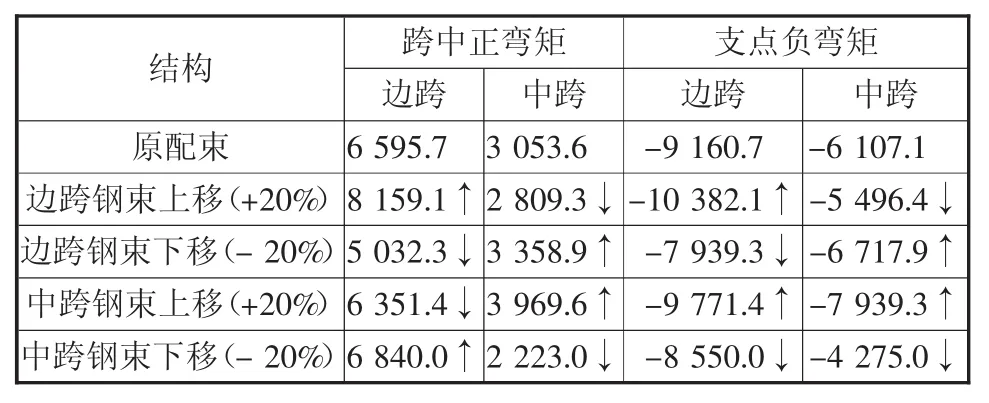
表4 4跨结构调束内力汇总表kN·m

从表4可以看出：

a）对于跨中正弯矩 边跨钢束上移，边跨跨中正弯矩增大，中跨跨中正弯矩减小，下移作用相反；中跨钢束上移，中跨跨中正弯矩增大，边跨跨中正弯矩减小，下移作用相反。

b）对于支点负弯矩 边跨钢束上移，边跨支点负弯矩增大，中跨支点负弯矩减小，下移作用相反；中跨钢束上移，边跨、中跨支点负弯矩均增大，下移作用相反。

因此，调束方式分为两组，一组是边跨钢束上移与中跨钢束下移同时进行（初次布束），以减小中跨支点负弯矩；另一组是边跨钢束下移与中跨钢束上移同时进行，加大中跨支点负弯矩。

一般情况下，有时边跨支点负弯矩大，有时中跨支点负弯矩大，此时可通过上述两组方法进行两处负弯矩平衡分配。

4.2.4 5跨结构

计算结果见表5。

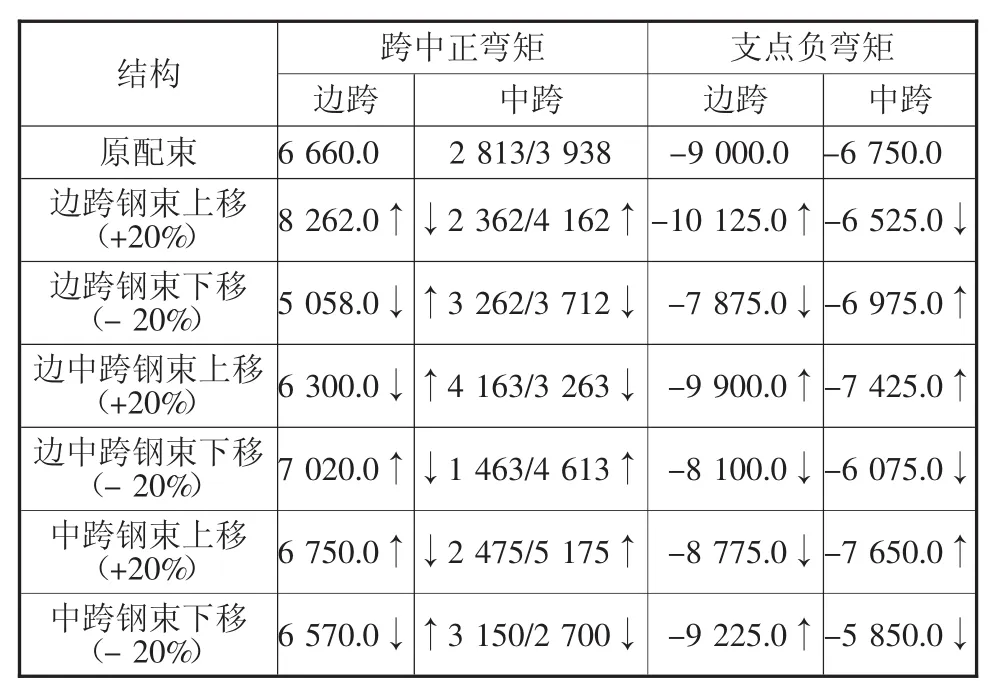
表5 5跨结构调束内力汇总表kN·m

从表5中可以看出，6种调束结果引起两种跨中正弯矩趋势，4种支点负弯矩趋势。

a）对于跨中正弯矩 边跨钢束上移、中跨钢束上移和边中跨钢束下移均引起边跨跨中、中跨跨中正弯矩增大，边中跨跨中正弯矩减小；边跨钢束下移、中跨钢束下移和边中跨钢束上移均引起边跨跨中、中跨跨中正弯矩减小，边中跨跨中正弯矩增大。

b）对于支点负弯矩 边跨钢束上移、中跨钢束下移引起边跨支点负弯矩增大，中跨支点负弯矩减小；边跨钢束下移、中跨钢束上移引起边跨支点负弯矩减小，中跨支点负弯矩增大；边中跨钢束上移，引起所有支点负弯矩增大；边中跨钢束下移，引起所有支点负弯矩减小。

由于5跨结构复杂，合理布束需根据初算确定最不利位置后用上述方法进行调束，以改善结构受力使之满足要求。

5 结论

通过对以上4种分跨形式的计算分析，总结出了预应力的配束线型对结构内力的影响趋势。综合来讲：

a）奇数跨较偶数跨合理；

b）2跨负弯矩值最大，3跨负弯矩值最小；

c）跨数越少受力越明确，跨数越多受力越复杂，故实际工程中3跨、4跨结构应用较多，2跨、5跨结构应用较少；

d）2跨、3跨结构边跨跨中预应力钢束重心尽量压低；

e）4跨、5跨结构应根据计算结果采用上述调束方法进行调试。

以上方法均针对各分跨跨中钢束重心位置进行的分析，支点处钢束重心的位置主要影响该支点处结构的抗力及应力，且受力模型及调整趋势较明确，此处不再进行分析。