基于改进LMI的鲁棒H∞动态输出反馈控制综合*
郝 峰,叶思隽,车晓涛
(1 西北工业大学航天学院,西安 710072; 2 中国兵器工业第203研究所,西安 710065)
基于改进LMI的鲁棒H∞动态输出反馈控制综合*
郝 峰1,2,叶思隽2,车晓涛2
(1 西北工业大学航天学院,西安 710072; 2 中国兵器工业第203研究所,西安 710065)
研究动态输出反馈(DOF)下连续时间系统的鲁棒H∞控制综合问题。借助于线性矩阵不等式(LMI)技术,给出了闭环系统鲁棒H∞DOF控制器存在的充要条件。该条件依赖于引入的松弛变量,消除了Lyapunov变量与系统矩阵之间的耦合,能够减小控制器设计的保守性。利用变量替换方法,将上述条件中的非线性矩阵不等式转化为关于替换变量的LMI,并给出了相应的DOF控制器求解方法。数值算例结果验证了新方法的有效性。
控制理论;鲁棒控制;动态输出反馈;线性矩阵不等式;H∞控制
0 引言
20世纪90年代以来,随着内点法的应用和MATLAB LMI工具箱的推出,LMI方法被广泛应用于控制领域[1-2],成为控制分析与综合最有效的工具之一。H∞控制是鲁棒控制理论中最为重要的设计框架之一。传统的H∞范数计算问题都可以通过有界实引理转化为标准的LMI表达式。但是,在多目标或多通道控制分析与综合时,矩阵表达式中的系统矩阵和Lyapunov变量之间的耦合导致问题非凸,难以求解。常见的解决办法是针对所有的约束条件使用相同的Lyapunov函数[2],这使得控制器的保守性大大增加。近年来,通过在矩阵表达式中引入松弛变量,能够实现系统矩阵和Lyapunov变量之间的解耦,减小设计保守性。M.C.Oliveira和J.Geromel在这方面做出了开创性的研究工作[3],获得了基于参数依赖Lyapunov函数的不确定离散时间系统的鲁棒稳定条件。其后,众多的控制学者[4-8]继续对这一问题进行了深入研究,并进一步将相关结果扩展至鲁棒H2、H∞控制问题以及D-稳定问题。但是,上述文献主要考虑了离散时间系统的参数依赖Lyapunov稳定性,而连续时间系统由于其稳定性条件所对应的LMI表达式自身的特点,难以实现Lyapunov变量与系统参数的解耦。如何将连续时间系统稳定性条件表述为依赖于松弛变量的LMI表达式,依然是鲁棒控制领域的难题。P.Apkarian[9]利用投影引理(projection lemma)和双边投影引理(reciprocal projection lemma)将文献[3]的结果推广到连续时间系统,并应用于特征结构配置和H2控制。P.J.de Oliveira[10]得到了适用于连续和离散时间系统的H∞鲁棒稳定条件。值得注意的是,以上这些方法的发展是与LMI松弛(LMI relaxations)技术的发展息息相关的,其应用于控制综合问题中的重要前提是能够消除Lyapunov变量与系统矩阵、控制增益的耦合。
同时,实际系统中的状态量往往不能全部获得,而测量输出获得部分信息是可行的。因此,输出反馈的研究更具有实际意义,已经成为控制领域一个重要的开放问题。输出反馈一般分为静态输出反馈(SOF)和动态输出反馈(DOF)。与SOF忽略控制器状态不同,DOF建立了完整的控制器状态空间描述,获得的控制效果更为出色。文献[2,11]总结了DOF控制综合中的两种方法:消元法和变量替换法。随后,文献[12-15]将借助不同LMI松弛方法得到的稳定性条件应用于DOF控制综合中。
文中针对连续时间系统,采用LMI松弛的方法,在稳定性条件对应的矩阵表达式中引入松弛变量,实现状态矩阵和Lyapunov变量的解耦,获得了保证系统鲁棒稳定的新的充要条件。该充要条件可以使用不同的Lyapunov变量处理多目标或多状态控制综合问题,能够降低设计保守性。同时,利用变量替换的方法,给出了满足上述稳定性条件的H∞鲁棒DOF控制器设计方法。该方法可以与参数依赖Lyapunov函数结合,应用于多目标/多通道控制综合问题中。
1 鲁棒H∞稳定的改进LMI条件
考虑以下的连续时间系统:
(1)
式中:x(t)∈Rn是状态变量;w(t)∈Rh是外部输入变量;z(t)∈Rp是可调输出变量;Tzw(s)=C(sI-A)-1B+D表示z(t)到w(t)的传递函数;A、B、C、D为给定的适当维数常值矩阵。
定义1[2](H∞控制问题)针对系统(1),给定H∞范数上界γ,寻找一个控制器K能够保证系统渐进稳定的同时满足以下的优化问题:

(2)
其中的H∞范数对应系统频率响应的最大奇异值的峰值,则称该控制器为系统(1)的鲁棒H∞控制器。
通过著名的有界实引理就可以将定义1中的H∞控制问题表示为一个标准的LMI表达式。
引理1[2](有界实引理) 对系统(1),设γ>0是一个给定的常数,则以下条件是等价的:
1)系统渐进稳定,且‖Tzw‖∞<γ;
2)存在一个对称矩阵P,使得:
(3)
可以看到式(3)中系统矩阵A和B与Lyapunov变量P之间存在乘积项。这导致在控制系统综合时只能使用同一个Lyapunov变量。下面将借助于LMI松弛的方法,通过在矩阵表达式中引入松弛变量实现系统矩阵与Lyapunov变量的解耦。在给出结论之前,首先介绍一个LMI松弛方法中的重要引理。
引理2[4](Finsler引理) 假设x∈Rn,Q∈Rm,A∈Rm×n,且A的秩满足rank(A) 1)xTQx<0,∀Ax=0,x≠0; 2)(A⊥)TQA⊥<0; 3)∃μ∈R:Q-μATA<0; 4)∃P∈Rn×m:Q+PA+ATPT<0。 Finsler引理已经成为LMI松弛过程中最重要的方法之一。接下来文中将利用引理2中的第二个和第四个表达式的等价关系,获得一个新的连续时间系统的鲁棒稳定条件。 定理1考虑连续时间系统(1),对于给定的H∞范数上界γ,如果存在对称正定矩阵P和矩阵V满足: (4) 则系统稳定且满足H∞性能指标。 证明: 充分性证明:令V=P,并将其代入式(4)中,得: (5) 根据Schur补引理[2],上式等价于: (6) 因为P>0,显而易见PAP-1ATP>0成立。将式(6)改写为: (7) 注意到式(7)左边的第一项与式(3)相同,因此式(7)成立则式(3)一定成立。根据引理2,可知满足式(4)则系统渐近稳定且‖Tzw‖∞<γ。 必要性证明:已知系统稳定且满足H∞性能指标,则根据引理2,系统满足式(3)。式(3)可以改写为以下形式: (8) 式中: (9) 根据引理2,式(8)等价于: (10) 显而易见,式(10)等价于式(4),定理1得证。 可以看到,在定理1中由于松弛变量T的引入,为H∞性能指标约束下的控制分析与综合问题提供了额外的自由度。并且,定理1可以方便的扩展到H2控制和D-稳定问题。但是,也应该注意到松弛变量T选择为一个较为特殊的形式:[V0000]T,可能会带来一定的设计保守性,在今后需要进一步研究。 2.1 问题描述 考虑以下的连续时间系统: z(t)=Czx(t)+Dzu(t) y(t)=Cx(t) (11) 式中:x(t)∈Rn是状态变量;u(t)∈Rm是控制输入;w(t)∈Rh是干扰输入;z(t)∈Rp是可调输出;y(t)∈Rp是输出变量;A、B、G、C、Cz、Dz为给定的适当维数常值矩阵。 本节的目的就是利用第二节中的改进LMI稳定条件,为系统(11)设计一个DOF控制器,使闭环系统稳定并满足H∞鲁棒性能指标。 对于系统(11),设其DOF控制器为: u(t)=CKxK(t)+DKy(t) (12) 式中:xK(t)∈Rk是控制器状态变量;AK、BK、CK、DK为需要求解的未知控制器增益矩阵。由式(11)和式(12)构成的闭环系统为: z(t)=Cclxcl(t) (13) (14) 2.2 控制综合 引理3考虑闭环系统(13),对于给定的H∞范数上界γ,如果存在对称正定矩阵Pcl和矩阵Vcl满足: (15) 则系统稳定且满足H∞性能指标。 引理3的证明过程与定理1类似,不再叙述。可以看到,将闭环系统状态变量Acl、Bcl、Ccl代入式(4)后,式(15)中的Lyapunov变量Pcl与控制器增益矩阵AK、BK、CK、DK以非线性的形式出现,难以直接求解。因此,下面借助文献[2,11]中的变量替换法,以新的变量代替原来的非线性项,将非线性矩阵不等式转化为LMI处理。 定理2考虑闭环系统(13),对于给定的H∞范数上界γ,如果存在对称正定矩阵P1、P3,矩阵X、X2、Y、Y2、U、P2满足: (16) (17) 式中: (18) 则闭环系统稳定且满足H∞性能指标。 证明: 令: (19) 易知: (20) 令: (21) 则式(20)可以简写成: VclF1=F2 (22) 根据式(14),式(19)~式(22)的表述,可知 (23) (24) 充分性证明:根据式(24)的表述,可将式(16)整理为: (25) AK= (26) 定理2实现了Lyapunov变量Pcl与系统矩阵和控制器增益矩阵之间的解耦。针对多目标或多状态优化问题,只需要对附加的松弛变量Vcl进行约束,就可以采用不同的Lyapunov变量Pcl处理不同的优化目标或系统状态,有效减小保守性。 考虑连续时间系统(11),令: 设DOF控制器为严格真,即DK=0。取H∞范数上界γ=10,根据定理2,利用MATLAB YALMIP工具箱[16]求得DOF控制器为: 为验证上述方法的有效性,利用文献[7]中的方法获得了类似定理1的状态反馈控制器: 并将两种方法进行比较。 分别采用上述两种控制器得到闭环系统的极点分布和H∞指标,如表1所示。从表1中可以看出,无论在DOF或状态反馈的情况下,闭环系统的极点均位于复平面的左半平面,即闭环系统是渐近稳定的。并且,在系统信息不完全的情况下,文中方法得到的DOF控制器依然能够保证系统的H∞性能与状态反馈基本一致,说明了文中方法能够有效减小控制器设计的保守性。 表1 闭环系统的极点分布和H∞性能 文中研究了连续时间系统鲁棒H∞动态输出反馈控制器设计问题。基于有界实引理和Finsler引理给出了满足H∞性能指标约束的鲁棒稳定的充要条件。通过在该条件中引入松弛变量,实现了对Lyapunov变量和系统矩阵的解耦。应用变量替换的方法,将输出反馈鲁棒控制器的可解条件化为标准的LMI,并给出了求解方法。数值算例的结果进一步说明了文中方法的可行性和有效性。 [1] BOYD S,CHAOUI L,FERRON E,et al.Balakrihnan V.Linear Matrix Inequalities in System and Control Theory [M].Philadelphia:SIAM,1994:85. [2] 俞立.鲁棒控制:线性矩阵不等式处理方法[M].北京:清华大学出版社,2002:102-108. [3] OLIVERIRA de M C,BERNUSSOU J,GEROMEL J C.A new discrete-time robust stability condition [J].Systems & Control Letters,1999,37(4):261-26. [4] OLIVERIRA de M C,SKELTON R E.Stability tests for constrained linear systems [C]//MOHEIMNI S O R.Perspectivesin Robust Control.London:Springer,2001,268:241-257. [5] SHAKED U.Improved LMI representations for the analysis and the design of continuous-time systems with polytopic type uncertainty [J].IEEE Transactions on Automatic Control,2001,46(4):652-656. [6] OLIVERIRA de M C,GEROMEL J C,BERNUSSOU J.Extendedandcharacterizations and controller parameterizations for discrete-time systems [J].International Journal of Control,2002,75(9):666-679. [7] 杨志红,马广富,李传江.基于扩展LMI的多目标状态反馈控制综合[J].电机与控制学报,2004,8(4):333-337. [8] PIPELEERS G,DEMEULENAERE B,SWEVERS J,et al.Extended LMI characterizations for stability and performance of linear systems [J].System & Control Letters,2009,58(7):510-518. [9] APKARIAN P,THAN H D,BERNUSSON J.Continuous-time analysis,eigen-structure assignment and synthesis with enhanced linear matrix inequalities (LMI) characterizations [J].IEEE Transactions on Automatic Control,2001,46(12):1941-1946. [10] OLIVERIRA de P J,OLIVERIRA R C L F,LEITE V J,et al.guaranteed cost computation by means of parameter-dependent Lyapunov functions [J].Automatica,2004,40(6):1053-1061. [11] SCHERER C W,GAHIENT P,CHILALI M.Multiobjective output-feedback control via LMI optimization [J].IEEE Transactions on Automatic Control,1997,42(7):896-911. [12] EBIHARA Y,HAGIWARA T.New dilated LMI characterizations for continuous-time multiobjective controller synthesis [J].Automatica,2004,40(11):2003-2009. [13] YANG R,LU L,XIE L H.Robust and control of discrete-time systems with polytopic uncertainties via dynamic output feedback [J].International Journal of Control,2005,16(10):1285-1294. [14] LEE K H,LEE J H,KWON W H.Sufficient LMI conditions for output feedback stabilization of linear discrete-time systems [J].IEEE Transactions on Automatic Control,2006,51(4):675-680. [15] GEROMEL J C,KOROGUI R H,BERNUSSON J.and robust output feedback control for continuous time polytopic systems [J].IET Control Theory Application,2007,1(5):1541-1549. ImprovedLMI-basedRobustH∞DynamicOutput-feedbackControlSynthesis HAO Feng1,2,YE Sijun2,CHE Xiaotao2 (1 School of Astronautics,Northwestern Polytechnical University,Xi’an 710072,China; 2 No.203 Research Institute of China Ordnance Industries,Xi’an 710065,China) The problem of robust H∞control synthesis based on dynamic output-feedback (DOF) for continuous-time systems is investigated.By using of Linear Matrix Inequality (LMI) technique,new sufficient and necessary condition for the existence of robust H∞DOF controller is derived.The condition eliminates the coupling of Lyapunov variable and system matrices by introducing slack variable to reduce the conservatism of controller design.The nonlinear matrix inequality in the proposed condition is converted into LMI about new variables based on variable substitution method.A numerical simulation example is given to demonstrate the effectiveness of the approach. control theory; robust control; dynamic output-feedback; linear matrix inequality; H∞control 10.15892/j.cnki.djzdxb.2017.02.002 2016-01-11 总装预先研究项目(1020702)资助 郝峰(1975-),男,陕西西乡人,高级工程师,博士研究生,研究方向:飞行器总体设计、飞行动力学与控制。 TP13 A

2 动态输出反馈控制综合
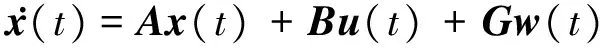





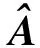
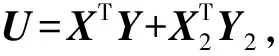
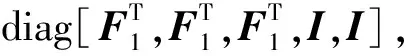
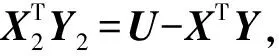
3 数值算例

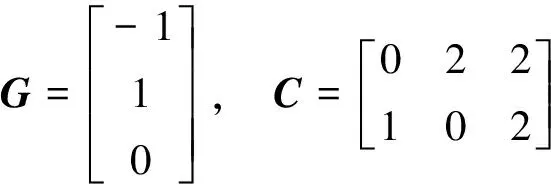

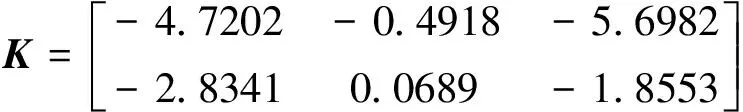

4 结论

