基于双外推法的污泥锯末共热解动力学分析
杨 凯,丁志江,肖立春,李 强
1.燕山大学国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛 066004;
2.燕山大学机械工程学院,河北 秦皇岛 066004;
3.燕山大学环境与化学工程学院,河北 秦皇岛 066004
基于双外推法的污泥锯末共热解动力学分析
杨 凯1,2,丁志江3,肖立春3,李 强1
1.燕山大学国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛 066004;
2.燕山大学机械工程学院,河北 秦皇岛 066004;
3.燕山大学环境与化学工程学院,河北 秦皇岛 066004
利用热重分析仪对污泥、锯末及其混合物进行了热重分析实验。基于双外推法,结合几种常规固体热解机理函数确定了污泥与锯末共热解过程最概然机理函数。结果表明:污泥与锯末按质量比9∶1混合共热解热重(DTG)曲线存在两个失重峰,主要热分解温度区间为 230~500 ℃,失重量约 47.1%;锯末的加入使混合物的表观活化能(E)降低,波峰出现右移;DTG波峰前后E值随升温速率增大有微小变化,且E与指前因子(A)之间具有动力学补偿效应;污泥与锯末共热解 DTG峰前(230~350 ℃)最概然机理函数为Nucleation-Growth(n=4)模型,峰后(350~500 ℃)为Chemical reaction(second order)模型。
污泥 锯末 热解 动力学 双外推法
城市污泥是城市污水厂污水处理的副产品,是城镇化和人口集聚带来的必然产物。随着我国城镇化的不断推进,城市污泥的处理处置问题开始引起重视。污泥中存在大量的细菌、病毒、有毒有机物和重金属等有毒有害物质[1,2],未经适当处理和处置的污泥会带来一系列的环境污染问题,而且污泥中的有机物含量很高,具有极大的经济利用价值,因此受到国内外学者的广泛关注。传统的污泥处理处置方法如填埋、堆肥和填海等存在对环境污染严重等缺点,已经逐渐被焚烧、热解和厌氧消化等方式取代[3],其中污泥热解可以极大地利用污泥的经济价值,符合国家“减量化、稳定化、无害化和资源化”的政策要求。
由于污泥的成分复杂,热解过程所发生的化学反应与各种操作条件的难以确定性,使得污泥的热解机理的建模十分困难,国内外学者对污泥热解机理进行了大量研究。Shao等[4]利用热重分析和红外光谱法对污泥热解及动力学机理的不同阶段进行了讨论,发现两种预干化污泥均存在两个热解阶段。Fang等[5]对造纸污泥和城市固体垃圾共热解进行了热重分析,采用 Flynn-Wall-Ozawa法和Kissinger-Akahira-Sunose法对其表观活化能进行计算,得到混合比例不同的样本表观活化能。Jayaraman等[6]利用热重-质谱(TG-MS)联用方法对芒草与污泥的热解、燃烧和气化特性进行了研究,发现温度、气氛及生物炭中的灰分对热处理过程有重要影响。翟云波等[7]对不同粒径的城市污泥燃烧和热解动力学进行了研究,得到了燃烧与热解不同阶段的活化能与反应级数。邵瑞华等[8]研究了污水处理厂污泥在制备泥质活性炭过程中的热解机理,采用双外推法确定了活化污泥的最概然机理函数。冉景煜等[9]采用热重分析法,研究了单一和混合工业污泥的热解动力学机理与特性,得到了不同条件下的热解特征温度与特征指数。常风民等[10]对污泥和煤进行了共热解实验与动力学理论分析,发现两者存在一定的协同效应。国内外学者对单一污泥和与有机添加剂共同热解动力学研究取得了一定的成果,但都集中于干燥污泥成分的热解特性及机理,且对其最概然机理函数的推断大都选取不同反应级数下的固定机理函数。此外,锯末作为生物质添加剂的加入可提高污泥有机质的比例,降低污泥热解过程活化能,提高液态气态产物产量,而国内外对污泥与锯末共热解过程的热解特性及其动力学的研究鲜有报道。为了对用锯末做骨架构建体[11,12]强化机械脱水后泥饼的进一步处理处置,以达到污泥减量化、无害化和资源化的目的,本工作对污泥与锯末共热解过程的热解特性及动力学进行了研究,结合Flynn-Wall-Ozawa法和Coats-Redfern法,采用双外推法确定了其最概然机理函数,为污泥锯末共热解的工艺开发与设计提供理论参考。
1 实验部分
1.1 实验材料
使用的污泥样本取自河北省秦皇岛市第三污水处理厂带式压滤机压滤后泥饼,含水率约80%,锯末取自秦皇岛某家具厂。污泥样品在 105 ℃电热恒温鼓风干燥箱内干燥至恒重,干燥污泥和锯末经研磨后通过约150 µm(100目)标准筛筛分,再根据所需比例制备干燥实验样本。污泥与锯末的工业分析和元素分析如表1所示,表中Mad,Vad,FCad和Aad分别为空气干燥基样本的含水量、挥发分、固定碳和灰分。

表1 样本的工业分析与元素分析Table 1 Primary analysis and ultimate analysis of samples
1.2 热重分析
样本热重分析(TG-DTG)实验采用日本岛津公司生产的DTA-60AH差热热重同步分析仪,装填样品质量约为5~15 mg,温度由程序设定从室温升至900 ℃,升温速率为10~30 ℃/min,热重实验载气为99.999%高纯氮气,气体流量为25 mL/min,系统自动记录实验过程的热量和质量变化,得到TG/DTG数据曲线。
2 热重实验结果与分析
如表1所示,污泥与锯末的组分不同,锯末的挥发分及有机相含量大于污泥,灰分含量远小于污泥。锯末具有良好的助脱水特性,向湿污泥中加入适量锯末,前期压滤脱水实验研究[12]表明,污泥与锯末按干基质量比9∶1添加可以满足污泥脱水率要求,提高干泥饼的热值,还可以较大程度地增大湿污泥的日处理量。为解决压滤后泥饼的处置问题,本工作将干污泥与锯末按干基质量比 9∶1进行混合热解,并将其TG和DTG曲线分别与污泥和锯末进行比较,结果见图1和2。
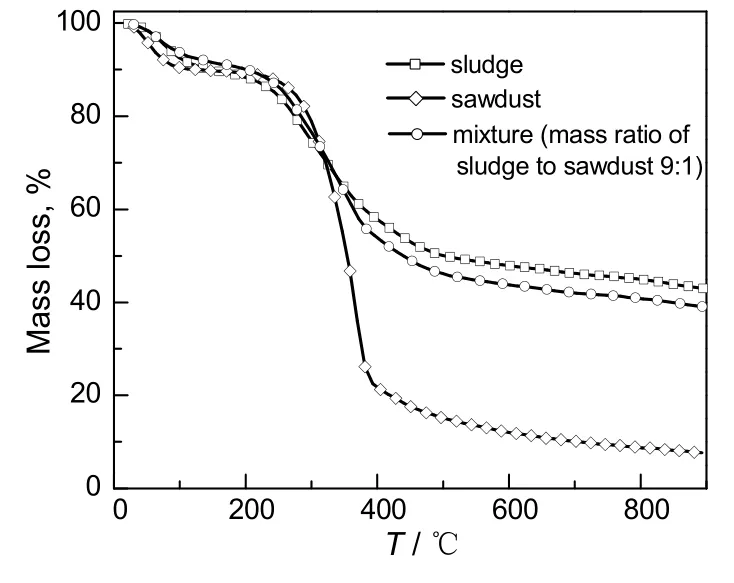
图1 污泥、锯末及其混合物的TG曲线Fig.1 TG curves of sludge, sawdust and their mixture
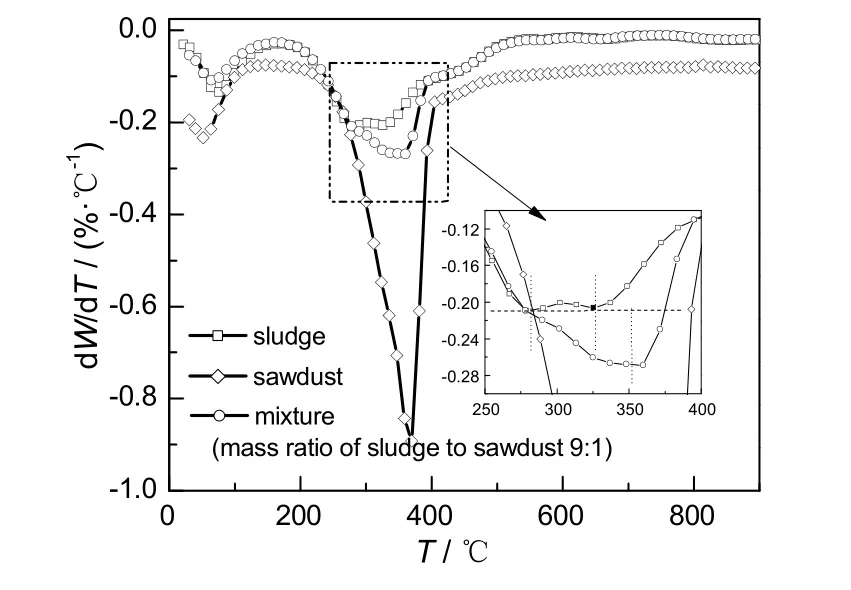
图2 污泥、锯末及其混合物的DTG曲线Fig.2 DTG curves of sludge, sawdust and their mixture
由图1和2可知,污泥和锯末都存在两个明显的失重阶段,在DTG曲线中对应两个较大的失重峰,其中在120 ℃左右的失重峰是由于样品中吸附水和结合水的析出引起的,该阶段的失重量约为8.9%。从DTG曲线对比可以看出,锯末在第二个失重峰处(210~380 ℃)的失重速率和失重量远大于污泥。锯末的主要成分是半纤维素和纤维素,其分解的主要温度区间为198~398和300~350 ℃[13],这和实验得到的曲线基本吻合,在此阶段失重量为65.0%。污泥的第二个失重峰对应温度区间为230~460 ℃,失重量为40%。污泥中有机物主要是脂肪类、蛋白质类和多糖类化合物等,其对应的分解区间分别为 300~400,250~350和 250~380 ℃[14]。污泥的 DTG曲线在第二个失重峰阶段存在两峰一谷,波谷温度约为320 ℃。这是由于各类化合物之间化学键差异不大,当达到其各自化学键断裂和基团转化变性温度时,陆续分解反应而出现了两个大部分重叠的失重峰。在第二个失重峰之后,污泥和锯末经历了较为缓慢的失重阶段,锯末失重量约为18.0%,这主要是木质素(失重温度410~540 ℃)等其他无机化合物的分解引起,而该阶段污泥的失重量约为8.0%,主要是残留有机物、矿物质和金属盐等无机物的分解引起。
由图1还可以看出,污泥与锯末混合物的热解终态温度与污泥相比没有明显变化,热解残渣有所减少,但主要分解温度区间内分解速率更大。混合物的DTG曲线中出现两个明显的失重峰,与纯污泥相比,由于混合物中加入了锯末,其表观活化能有所降低,失重速率增大,波峰也出现右移,该温度区间(230~500 ℃)主要是易分解有机物的裂解阶段,失重量约 47.1%。此后,试样中无机盐、残留有机物等物质缓慢分解,失重量约6.2%。
图3为污泥和锯末混合样品在不同升温速率下的热重图。由图可知,热解残渣随着升温速率的增大而增多,最大失重速率随着升温速率的增大而变小,波峰稍有偏移的趋势。这是由于样本在加热过程中会受到颗粒内部与外部传热过程的影响,表现出局部的非热平衡状态,而较高的升温速率会缩短样本热解反应时间,使这种局部非热平衡的状态更加明显,气态产物不能及时析出也阻碍了热解反应的顺利进行。
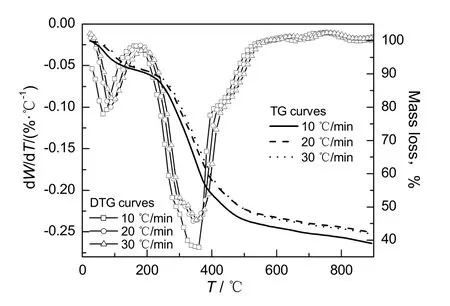
图3 不同升温速率下混合物的TG/DTG曲线Fig.3 The TG and DTG curves of mixture samples at different heating rates
3 污泥与锯末共热解动力学分析
3.1 动力学模型及计算方法
污泥与锯末共热解的动力学过程不能用单一的机理函数进行描述[15],本工作对DTG曲线第二失重峰波峰前后分别采用不同的热解机理模型进行描述。在对波峰前后进行模型函数确定时,传统的计算方法忽略了样本热传导造成的样品和环境之间的非热平衡,计算结果与真实情况存在一定的偏差,尤其是当升温速率较快的情况下,这种非热平衡状态更加明显。为了更加准确地确定反应模型,引入了双外推法:首先将加热速率外推为0,当无限减小加热速率时,可以认为样本与环境之间处于热平衡状态,此时就可得到样本处于热平衡状态时的热动力学参数。随后,由于样本在不同转化率时,其热动力学参数呈规律性变化[8],再将转化率也外推为 0,计算得到的参数可认为是样本处于原始状态的参数。最后,将加热速率与转化率双双外推为0后的结果进行对比选择,可确定样本热解反应过程的最概然机理函数,具体计算方法如下:
固相热解过程可以用以下反应描述:

式中:A是污泥与锯末的固态混合样本;B是热解后的固态残留物;C为热解产生的气体。假定该反应是不可逆反应,此时反应转化率(α,%)表示为:

式中:m0为初始质量;m1为终态质量;m为在任意t时刻时样本质量。由Arrhenius公式确定样本的分解速率为:

式中:β为升温速率,K/min;f(α)为热解机理函数;A为指前因子,min-1,E为反应的表观活化能,kJ/mol;R为气体常数;T为绝对温度,K。
根据Coats-Redfern法,通过积分法对公式(3)进行积分并取对数后得到:

式中:G(α)为机理函数的积分形式。对于一般温度范围内的反应,大部分E值,E/(RT)远大于1,故式(4)可转化为:

此时,在升温速率β不变的情况下,ln[G(α)/T2]与T-1呈线性关系,拟合数据的斜率即可求得表观活化能E。常用的固相热解机理函数的积分形式见表2。将表2中几种常规固体机理函数[16]代入公式(5)求得不同升温速率下的表观活化能,根据公式(6)将数据拟合并将升温速率 β外推为 0,得到热平衡状态下的极限表观活化能Eβ→0。

式中:Eβ为β拟合活化能;b1为拟合常数;k1,k2和k3为β各次方项系数。

表2 常规固体热解反应机理函数Table 2 Mechanism functions of conventional solid pyrolysis
根据Flynn-Wall-Ozawa公式:
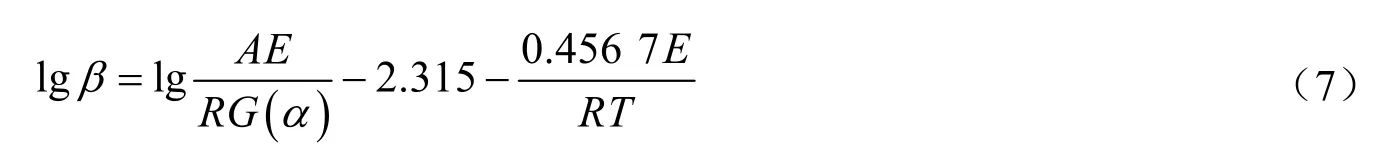
由上式可知,当转化率α一定时,G(α)为定值,lgβ与T-1呈线性关系,其斜率为-0.456 7E/R,据此斜率可求出E。因此Flynn-Wall-Ozawa法可以避免选择机理函数而直接求出E值。将不同转化率时求得的E值根据公式(8)进行拟合。

将转化率α外推为0,得到原始状态下的极限表观活化能Eα→0。将不同机理函数下得到的热平衡状态下的极限表观活化能Eβ→0与Flynn-Wall-Ozawa法求得的Eα→0进行对比,选取相近值时的函数即为热解过程的最概然机理函数积分式。
3.2 计算结果及分析
各类型固相反应机制的典型函数根据Coats-Redfern法对ln[G(α)/T2]与T-1拟合情况如图4和5所示。由图可看出,尽管大部分机理函数的拟合线性相关性均较好,但样本热解的最概然机理函数还需要进一步与原始状态下的极限表观活化能对比才能确定。由 Coats-Redfern法及常规固体热解机理函数在5种升温速率下计算得到的结果见表3。由表可知,随着升温速率β的增加,通过各种机理函数求得的第二个失重峰峰前热解表观反应活化能均有所降低,而随着β的增加,第二个失重峰峰后热解表观活化能呈现出增加的趋势。虽然E的变化都不大,但是E的增大和减小,均伴随着指前因子A的增大和减小,E和A之间存在着相互补偿的关系,即“动力学补偿效应”,这与Li等[17,18]的研究结果一致。主要因为当升温速率增大时,受传热影响,样本内部及周围环境的温度梯度增大,非热平衡状态会影响气态产物的生成和溢出。此外升温速率增加还会缩短热解反应的时长,影响反应进程。随着热解进程的推进,DTG波峰之后样本的密度、传热系数等物化参数、结构等都发生了较大变化,使得热解发生需要更多的能量。

图4 升温速率为10 ℃/min时峰前函数拟合曲线Fig.4 Fitting curves of pre-peak at β=10 ℃/min
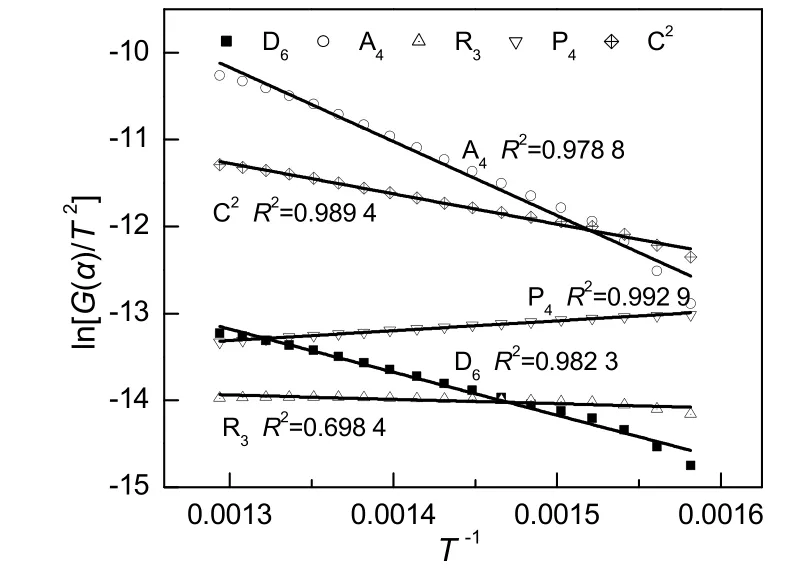
图5 升温速率为10 ℃/min时峰后函数拟合曲线Fig.5 Fitting curves of post-peak at β=10 ℃/min

表3 采用Coats-Redfern法计算污泥与锯末混合物DTG第二个失重峰峰前和峰后(230~350 ℃)热解表观反应活化能Table 3 Apparent activation energy of mixture before and after DTG’s second peak (230-350 ℃) by Coats-Redfern method
通过Flynn-Wall-Ozawa法计算得到固定转化率时的表观活化能E后,将其按公式(8)拟合后所得函数如下式所示:

由式(9)可知,波峰前后原始状态下的极限表观活化能Eα→0分别为138.01和29.28 kJ/mol。对比表3可以看出,样本在DTG峰前热平衡状态下,使用Nucleation-Growth(n=4)机理模型计算的极限表观活化能Eβ→0为126.9 kJ/mol,与由Flynn-Wall-Ozawa法计算得到的Eα→0为138.01 kJ/mol最接近。因此,污泥与锯末共热解过程 DTG峰前最概然机理函数为 Nucleation-Growth(n=4)模型,由Flynn-Wall-Ozawa法确定此阶段表观活化能均值为170.05 kJ/mol。
由表3中可以看出,样本在DTG峰后热平衡状态下,采用Chemical reaction (second order)机理模型计算的极限表观活化能Eβ→0为27.61 kJ/mol,与由Flynn-Wall-Ozawa法计算得到的Eα→0为29.28 kJ/mol最接近。因此,污泥与锯末共热解过程 DTG峰后最概然机理函数为Chemical reaction (second order)机理模型,由Flynn-Wall-Ozawa法确定此阶段表观活化能均值为178.13 kJ/mol。
为了验证计算结果的准确度,对样本在升温速率为10 ℃/min的条件下进行了3次重复性实验,并将由上述机理模型计算得到的理论TG曲线与实验TG曲线进行了对比,如图6所示。可以看出,实验TG曲线均与模型计算TG曲线基本吻合,且最大偏差不超过5%,说明该模型可行。

图6 实验与理论TG曲线对比Fig.6 Comparison of experimental and theoretical TG curves
4 结 论
a)污泥与锯末按质量比为 9∶1混合共热解的主要热分解温度区间为 230~500 ℃,失重量约47.1%。锯末的添加会降低混合物的表观活化能。随着升温速率的增大,热解残渣逐渐增多,最大失重速率减小,DTG波峰出现偏移。
b)随着升温速率的增大,波峰前后表观活化能分别呈现增大和减小的趋势,表观活化能与指前因子间符合动力学补偿效应。双外推法确定了污泥与锯末共热解最概然机理函数:DTG峰前为Nucleation-Growth(n=4)模型,峰后为Chemical reaction (second order)机理模型。
[1]Smith K M, Fowler G D, Pullket S, et al.Sewage sludge-based adsorbents: a review of their production, properties and use in water treatment applications[J].Water Research, 2009, 43(10): 2569-2594.
[2]Pritchard D L, Penney N, Mclaughlin M J, et al.Land application of sewage sludge(biosolids) in Australia: risks to the environment and food crops[J].Water Science and Technology, 2010, 62(1): 48-57.
[3]胡艳军, 郑小艳, 宁方勇.污水污泥热解过程的能量平衡与反应热分析[J].动力工程学报, 2013, 33(5): 399-404.Hu Yanjun, Zheng Xiaoyan, Ning Fangyong.Analysis on energy balance and reaction heat of sewage sludge pyrolysis process[J].Journal of Chinese Society of Power Engineering, 2013, 33(5): 399-404.
[4]Shao J, Yan R, Chen H, et al.Pyrolysis characteristics and kinetics of sewage sludge by thermogravimetry fourier transform infrared analysis[J].Energy Fuels, 2008, 22: 38-45.
[5]Fang S, Yu Z, Lin Y, et al.Thermogravimetric analysis of the co-pyrolysis of paper sludge and municipal solid waste[J].Energy Conversion and Management, 2015, 101(13): 626-631.
[6]Jayaraman K, Gokalp I.Pyrolysis, combustion and gasification characteristics of miscanthus and sewage sludge[J].Energy Conversion and Management, 2015, 89(1): 83-91.
[7]翟云波, 彭文锋, 蒋剑虹, 等.不同粒径城市污泥热解和燃烧动力学研究[J].湖南大学学报(自然科学版), 2012, 39(3): 66-70.Zhai Yunbo, Peng Wenfeng, Jiang Jianhong, et al.Research on the pyrolysis and combustion kinetics of sewage sludge of different sizes[J].Journal of Hunan University, 2012, 39(3): 66-70.
[8]邵瑞华, 房 平.城市污水处理厂污泥制备活性炭过程中活化污泥的热解动力学[J].过程工程学报, 2013, 13(2): 217-223.Shao Ruihua, Fang Ping.Pyrolysis kinetics of activated sewage sludge in preparation of sewage sludge-based activated carbon[J].The Chinese Journal of Process Engineering, 2013, 13(2): 217-223.
[9]冉景煜, 王裕明, 牛立祥, 等.混合工业污泥热解及动力学特性实验研究[J].工程热物理学报, 2009, 30(3): 509-512.Ran Jingyu, Wang Yuming, Niu Lixiang, et al.Experiment on pyrolysis and kinetic characteristics of mixed industrial sludge[J].Journal of Engineering Thermophysics, 2009, 30(3): 509-512.
[10]常风民, 王启宝, 王凯军.城市污泥与煤混合热解特性及动力学分析[J].环境工程学报, 2015, 9(5): 2412-2418.Chang Fengmin, Wang Qibao, Wang Kaijun.Thermogravimetric characteristics and kinetic analysis of co-pyrolysis of sewage sludge and coal[J].Chinese Journal of Environmental Engineering, 2015, 9(5): 2412- 2418.
[11]燕山大学.一种城市污水处理厂污泥燃料化处理工艺方法: 中国, 201210317629X[P].2012-12-19.
[12]郭 杰.城市污水处理厂污泥燃料化技术[D].秦皇岛: 燕山大学, 2012.
[13]Han R, Zhao C, Liu J, et al.Thermal characterization and syngas production from the pyrolysis of biophysical dried and traditional thermal dried sewage sludge[J].Bioresource Technology, 2015, 198(24): 276-282.
[14]闫志成.污水污泥热解特性与工艺研究[D].哈尔滨: 哈尔滨工业大学, 2014.
[15]Folgueras M B, Ramons M D, Jorge X, et al.Thermogravimetric analysis of the co-combustion of coal and sewage sludge[J].Fuel, 2003,82(15): 2051-2055.
[16]沈 兴.差热、热重分析与非等温固相反应动力学[M].北京: 冶金工业出版社, 1995: 169-180.
[17]崔 洪, 朱珍平, 刘振宇, 等.程序升温热重法研究扎赉诺尔煤的气化动力学[J].燃料化学学报, 1996, (5): 23-27.Cui Hong, Zhu Zhenping, Liu Zhenyu, et al.Gasification kinetics of zl coal using TG/DTG method[J].Journal of Fuel Chemistry and Technology, 1996, (5): 23-27.
[18]Li S, Cheng Y.Catalytic gasification of gas-coal char in CO2[J].Fuel, 1995, 74(3): 456-458.
Kinetic Analysis of Co-Pyrolysis of Sewage Sludge and Sawdust Based on Double Extrapolation Method
Yang Kai1,2, Ding Zhijiang3, Xiao Lichun3, Li Qiang1
1.National Engineering Research Center for Equipment and Technology of Cold Strip Rolling, Yanshan University,Qinhuangdao 066004, China;
2.College of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China;
3.College of Environmental and Chemical Engineering, Yanshan University, Qinhuangdao 066004, China
The thermogravimetric analysis experiment on sludge, sawdust and their mixture were carried out by thermogravimetric analyzer.Based on the double extrapolation method, the most probabilistic mechanism functions of the co-pyrolysis process of the mixture were obtained by combining several conventional solid pyrolysis mechanism functions.The results showed that there were two weight loss peaks in the DTG curve with mass ratio of sludge to sawdust 9:1.The main decomposition temperature range was 230-500 ℃ with a weight loss of about 47.1 %.The addiction of sawdust reduced the apparent activation energy (E) of the mixture and the peak appeared to shift to the high temperature.The E value of DTG peak varied slightly with the increase of heating rate, and there was a kinetic compensation effect between E and pre-exponential factor (A).The most probable mechanism functions of co-pyrolysis of the mixture before and after the DTG peak (230-350 and 350-500 ℃) were the Nucleation-Growth (n=4) and Chemical reaction (second order),respectively.
sewage sludge; sawdust; pyrolysis; kinetic; double extrapolation method
X705
A
1001—7631 ( 2017 ) 04—0356—08
10.11730/j.issn.1001-7631.2017.04.0356.08
2017-07-03;
2017-08-16。
杨 凯(1989—),男,博士研究生。李 强(1962—),男,教授,通讯联系人。E-mail: liqiang@ysu.edu.cn。
河北省科技计划项目(16C1303351005);河北省自然科学基金项目(E2015203236)。

