深海布放缆不同材料属性下应力波自由传播频率特性影响研究

吴丞昊，杨建民，田新亮，胡智焕，彭 涛

(上海交通大学 海洋工程国家重点实验室高新船舶与深海开发装备协同创新中心，上海 200240)

深海布放缆不同材料属性下应力波自由传播频率特性影响研究

吴丞昊，杨建民，田新亮，胡智焕，彭 涛

(上海交通大学 海洋工程国家重点实验室高新船舶与深海开发装备协同创新中心，上海 200240)

在频域对深海布放缆系统内应力波自由传播特性进行了分析。在布放缆数学建模时使用了哈密顿原理，并在建模时考虑布放缆的曲率。计算过程中保留了缆绳曲率与其弧长坐标之间的非线性关系，并最后得到了其上传播的应力纵波与应力横波的特性。通过计算得到布放缆属性和缆绳内竖直张力等参数对缆绳内自由传播频率特性的影响曲线。结果表明，这些因素对自由传播应力波的频率关系、色散关系、相速度与群速度影响显著。对于应力纵波，整个频域可被两个截止频率与一个行波截止频率分成四个区域。除了通频带之外，在低频时亦存在抑止带和行波抑止带。应力纵波仅能在通频带中以行波形式传播，而应力横波则可以在所有频率范围内以行波形式传播。

应力波；深海布放；张紧松弛；突加载荷

随着人类对深海资源开发的逐渐加速以及深海生产设备技术的进步，位于3500米及更深处的深海开发日益受到重视。为了适应大规模深海开发，各类深海开发装备的质量与体积也与日俱增。布放回收装置担负着将所有水下系统安全、可靠、平稳地布放到海底以及将其从海底回收到水面的使命。国内外各项研究表明，在遇到复杂海情的情况下，缆绳系统可能出现高速传播的突加应力，其大小甚至可能达到平均张力的十倍[1-2]，对系统整体安全造成了巨大威胁。相比现有的较浅的海洋设备布放系统，深海布放所需的缆线相对更长、所受载荷更重。目前世界上学者对深海布放系统基于叠加驻波的模态研究已经较为深入，然而对系统内应力波的传播过程和衰减的研究则相对较少。由于深海长缆线中的应力传播时间与系统特征时间同数量级，在这种条件下，应力波是一个不应被忽视的因素[3]。因此，为了设计更安全更经济的布放缆线系统，了解深海布放长缆系统中应力波的产生和传播特性显得尤为重要。

Poisson S D[4]最先对固体介质中传播的行波进行了理论研究，并发现在固体介质中可以传播两类行波(纵波与横波)，A L B Cauchy 的经典著作[5]中亦得到了相同结论。K F Graff,et al.[6]在总结了前人对弹性行波研究的基础上，沿用经典方法研究了在系泊缆与悬链线缆中的应力行波传播。其计算中不仅考虑了缆绳的质量与曲率，同时考虑了浸没液体中缆绳受到的水动力作用。M Behbahani-Nejad和N C Perkins 使用Hamilton原理推导了在小下垂率假设下的悬链缆线性控制方程，得到了自由传播的结构波动态响应曲线[7]，并使用解析和数值方法分别在频域与时域上研究了简谐波在缆上传播的响应特性[8]，研究发现，应力纵波在传播过程中表现为高度色散，而应力横波则表现出非色散特性，且初始张力扰动会导致两列应力波以不同的速度进行传播，而这点是传统准静态缆绳张力理论所不能预见的。W J Kim 和N C Perkins随后对系泊浮标下的受拉张紧系泊缆进行了数学建模，将其线性化后得到了其频域响应曲线[9]。他们也对一个弹性缆绳系统在流激励下的共振响应进行了研究[10]。 张素侠等人研究了系泊缆在松弛-张紧变换状态下的应力波在钢缆上传播的频率响应[11]，发现缆绳频率、群速度与频散曲线沿缆绳弧长方向变化较大。Abedinnasab M H,et al分别研究了绳索中[12]和Euler-Bernoulli柱[13]在有限变形下的应力波色散曲线。近年来，王礼力等人在其著作中[3]全面地总结了应力波在不同介质中传播的控制方程、推导过程及其时域频域特征，为之后的研究者提供了良好的学习参考。

除了使用解析方法对应力波的特征进行分析以外，应力波在不同条件下的数值计算也引起了研究者的广泛兴趣。Bezverkhii等人和Shul’ga等人在Hamilton原理基础上进一步推出了一套缆绳中应力波传播的连续-离散偏微分数值计算模型，并用该模型计算了系泊缆[14,15]和水下多缆拖曳系统[16-18]等情况下系统中的应力时域曲线。同时在该研究基础上，又在公式中增加了对缆绳材料非线性影响的考虑[14,16]。然而其数值计算主要集中在时域上缆绳应力的动态响应分析，在频域的相关分析稍显不足。

本文用理论解析求解的方式分析深海布放缆线系统中应力波自由传播的频域特性，并引入缆内水平张力与缆单位长度湿重之比λ1、缆内竖直张力与缆单位长度湿重之比λ2来表现布放缆受到的水平与竖直张力对其上应力波的传播影响，同时通过弹性模量与材料密度的变化(表现为cl的变化)表现不同缆绳属性对应力波频率特性的影响。计算中保留了缆绳曲率与其弧长坐标之间的非线性关系，并发现了非线性对应力横波传播特性的影响。结果以期为工程布放应用安全提供参考。

1 缆绳数学模型

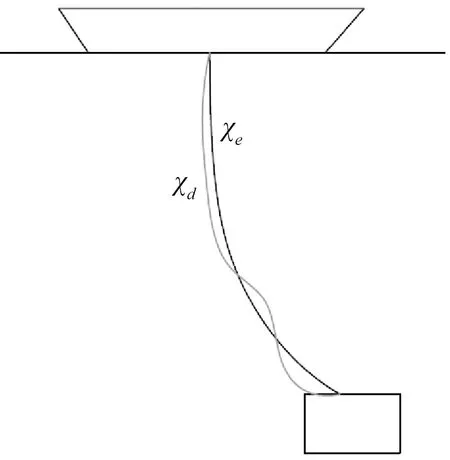
图1 平衡状态布放缆模型χe与动态布放缆模型χdFig.1 Cable model in equilibrium configuration χe and in dynamic configuration χd

根据Perkins理论[19]， 可以视布放缆线为一个在三维空间中运动的可忽略弯曲刚度及扭转刚度的一维弹性连续体，于此同时其内部编制结构对布放系统内应力波传播的影响也被忽略，即将其考虑为一整根完整连续的一维弹性连续体。布放缆绳模型如图1所示，其在平衡状态下的构型为χe，而当应力波在其上传播时，其平衡状态会被打破，此时处于不稳定状态下的布放缆构型为χd。布放缆运动可以被分解为3个方向：切向、法向与副法向，本文仅考虑其在面内的运动。定义切向位移为u1，法向位移为u2，它们对t的偏导数分别为u1,t，u2,t，即切向与法向运动速度对s的偏导数u1,s，u2,s分别为切向与法向应变。忽略缆绳在流体介质中的阻尼，其面内运动的运动方程为：

(1+Cm)ρlAu1,tt=[(P+EAε)(u1,s-κu2)+EAε],s-κ(P+EAε)(u2,s+κu1)+F1

(1)

(1+Cm)ρlAu2,tt=[(P+EAε)(u2,s+κu1)],s+κ[(P+EAε)(u1,s-κu2)+EAε]+F2

(2)

式中：s为缆绳的弧长坐标，A为缆绳的截面积，E为缆绳的弹性模量，P1为布放缆张力竖直方向分量，P0为布放缆张力水平方向分量，F1和F2为系统所受的外力。缆绳在s处的动态应变ε(s,t)、布放缆平衡张力P(s,t)及曲率κ(s,t)分别为：

式中：ρ=ρl-ρw，其中ρl为缆绳材料密度，ρw为流体介质密度，Cm为缆绳附加质量系数，g为重力加速度。

由式(4)、(5)可以发现，缆绳的曲率κ(s,t)与弧长坐标s之间呈现非线性的关系。为了更好地保留缆绳曲率对频率特性的影响，在之后的计算中该非线性关系将被保留。

由于本文考虑应力波在深海布放缆线系统内的自由传播特性，因此忽略式中外力F1与F2。将式(3)、(4)、(5)代入式(1)与(2)并保留线性项，可以得到：

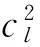
(6)

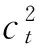
(7)

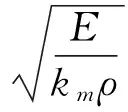
式(6)与式(7)可用矩阵表示为：

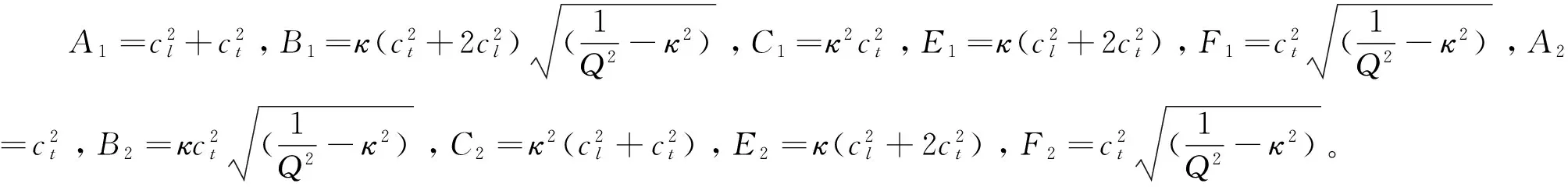
2 应力波传播特性

2.1频率关系

(9)

式中：C.C.代表式(9)前一项的共轭复数。将其代入方程(8)并对其进行空间傅里叶变换，可以得到：

通过求解式(11)，可以得到特征频率方程：

式中：

α1=(A1+A2)γ2-j(F1+F2)γ+C1+C2

通过求解式(12)可以获得四个频率解：纵波频率ω1,2=±ωl和横波频率ω3,4=±ωt，其中：

2.2色散关系

缆线系统内传播的应力波速度可分为相速度与群速度两个速度。对于色散的波传播系统，相速度与群速度将会分离，且波速依赖于频率。

2.2.1 相速度

一般将c=ω/γ称为相速度，将其代入频率关系式(12)，可以得到色散方程：

D(c;ω,cl,ct)=β1c4+β2ωc3-β3ω2c2-β4ω3c+β5ω4=0

(15)

式中：

β1=ω4-(C1+C2)ω2+(C1C2+B1B2)

β2=j[(F1+F2)ω2-(C1F2+E1B2+B1E2+F1C2)]

β3=(A1+A2)ω2+(F1F2-A2C1-A1C2+E1E2)

β4=j(F1A2+A1F2)

β5=A1A2

2.2.2 群速度

通过对频率关系式(12)进行直接微分，可以得到：

4ω3(dw)-(dα1)ω2-2α1ωdω+dα2=0

其中：

dα1=2γ(A1+A2)dγ-j(F1+F2)dγ

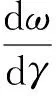
3 结果与讨论

为了更好地展示缆绳属性、缆绳受到的竖直与水平力等对缆绳内应力波传播的频率特性造成的影响，通过数值求解上述方程对其上应力波传播特性进行分析。在计算分析中，为了更好地拓展研究范围，本文在常见的工程应用布放缆材料属性之上更进一步地扩展了各属性的计算范围。

本文参考的复合缆属性为[20]：弹性模量E=12.4 GPa，密度ρl=1.44×103kg/m3。钢缆系统参数为[15]：弹性模量E=200 GPa，缆绳密度ρl=8×103kg/m3，Cm=0.13，由于cl与且仅与缆绳属性有关，为了覆盖从复合缆到钢缆的各种材料属性，同时拓展计算范围，本文在计算中取3 000 m/s≤cl≤8 000 m/s来观察不同材料属性对应力波传播特性的影响。水平与竖直方向张力与单位长度缆绳湿重之比的取值分别为λ1=500 m 及1 000≤λ2≤10 000 m。

3.1频率极限情况

本文首先关注布放系统的截止频率。在长波长/低频率极限时，传播常数γ→0，因此式(12)在低频极限时趋向于：

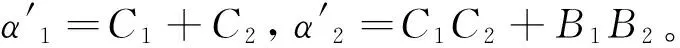
通过求解方程(16)，可以得到：

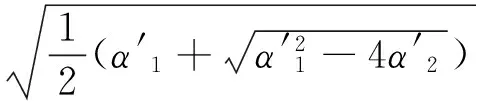
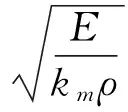
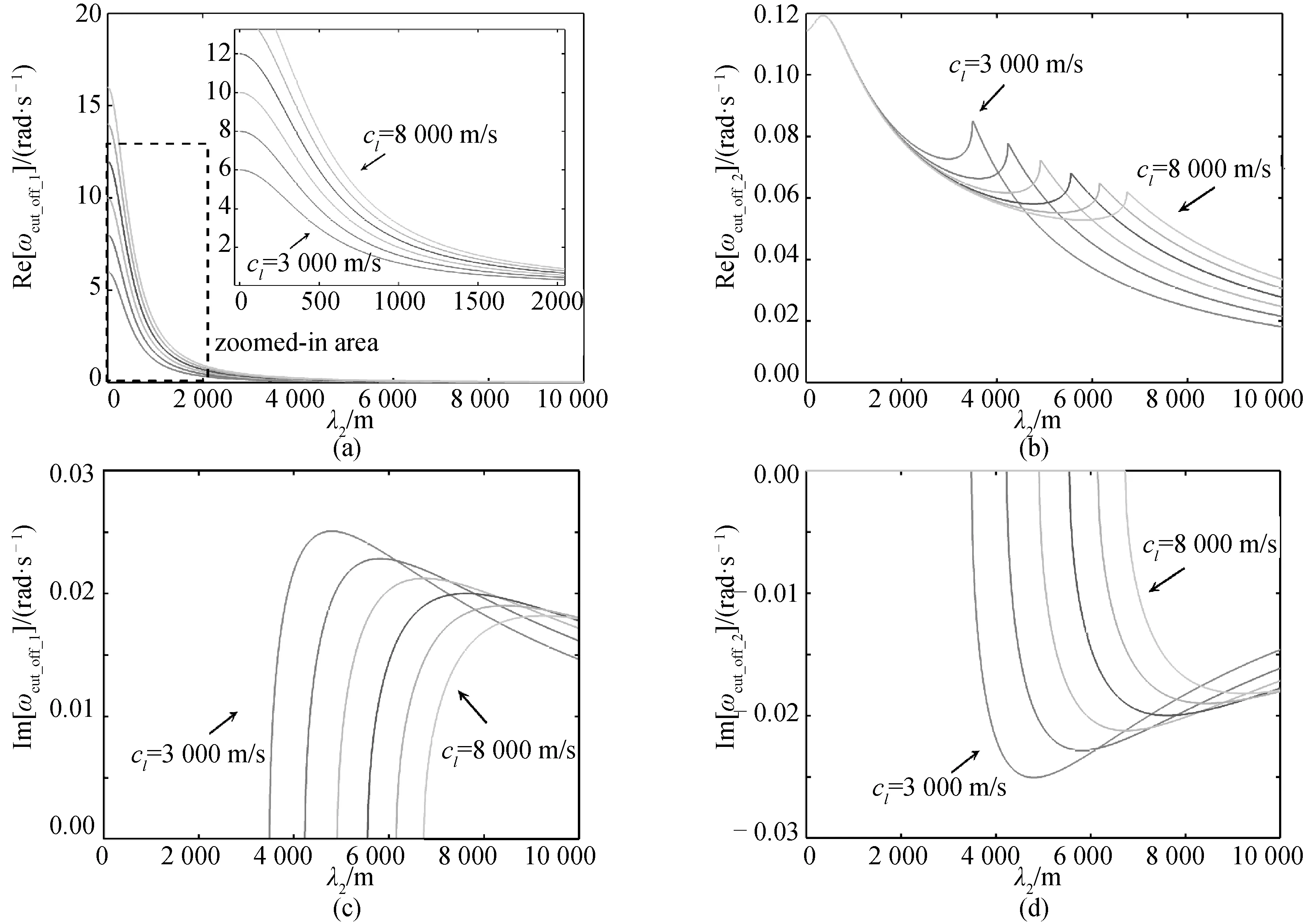
图2 两个截止频率实部((a)(b))及两个截止频率虚部((c)(d))(3 000 m/s≤cl≤8 000 m/s,λ1=500 m,0≤λ2≤10 000 m)Fig.2 Real parts of cut-off frequencies ((a)(b)) and Imaginary parts of cut-off frequencies ((c)(d)) (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,0≤λ2≤10 000 m)

从图2(b)中可以发现，绝对值较小的截止频率ωcut_off_2的实部并不随着λ2的增加而单调减少，而是可以观察到一个区域极大值。该极大值出现时所对应的λ2是区分该系统截止频率是否为纯实数的λ2临界值，当布放系统的λ2大于该极大值对应的λ2时，该系统截止频率不再是纯实数，而是一个复数。截止频率实部的极值出现时所对应的λ2的大小随着cl的增大而增大，即其出现位置对应的λ2随着布放缆弹性模量的增大而增大，随着布放缆密度的增大而减小，但该极值的幅值大小随着cl的增大而减小。当较小的截止频率在越过极值点后单调递减，且此时该截止频率大小随着cl的增大而增大。

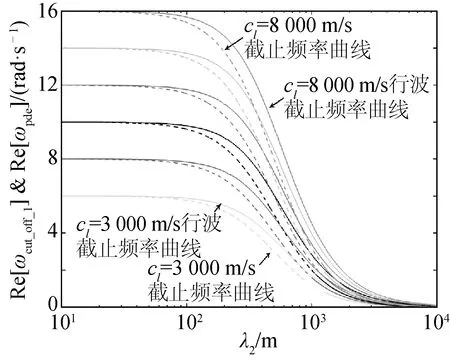
图3 实线: 行波截止频率实部大小随λ2变化曲线，虚线：截止频率实部大小随λ2变化曲线。横轴λ2为对数坐标(3 000 m/s≤cl≤8 000 m/s,λ1=500 m,0≤λ2≤10 000 m)Fig.3 Real part of cut-off frequencies (dashed curves) and pass-band edge frequencies (solid curves).λ2 is set on a logarithmic scale(3 000 m/s≤cl≤8 000 m/s,λ1=500 m,0≤λ2≤10 000 m)

在Re(γ)→0，即波数趋向于0时，可以得到另一个极限解：行波截止频率ωpde。只有大于该频率的应力波才能以行波的形式在布放缆介质中传播。图3中分别以实线和虚线展示了行波截止频率与截止频率随λ2的变化关系。

整个应力纵波的频域因而被两个截止频率与行波截止频率划分成了四个部分。如图4所示，当频率大于行波截止频率时，为通频带；行波抑止带存在于ωcut_off_1与行波截止频率之间，以及小于ωcut_off_2的频率范围；当两个截止频率为复数时，它们之间的区域仍然保持行波抑止带，而当两个截止频率为纯实数时，在它们之间的为抑止带。

另一方面，在短波长-高频极限，即γ→时，将式(12)左右分别除以γ4可以得到：

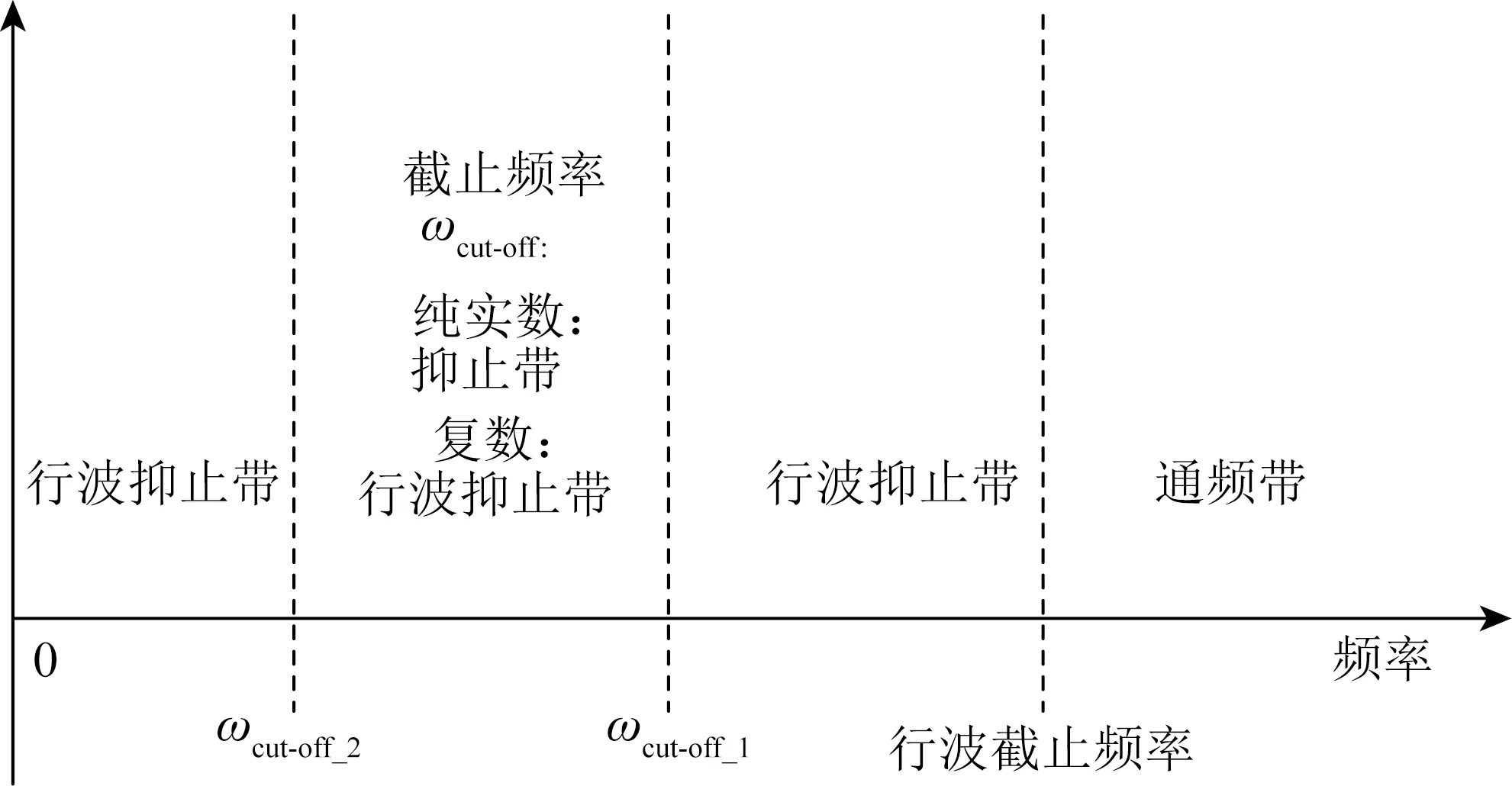
图4 系统频域上由截止频率和行波截止频率分成的四个不同频段示意Fig.4 Different bands of the spectral domain divided by cut-off frequencies and pass-band edge

3.2频率关系

根据式(13)与式(14)，可以计算得到缆绳内应力波的传播常数与频率的关系，计算得到的应力纵波、横波与频率关系分别如图5、图6所示。传播常数为复数，其实部为波数，虚部为衰减常数的相反数。波数的正负分别代表了波传播的两个方向。衰减常数表征应力波衰减方向与衰减率的大小。

图5显示了在不同缆绳属性的情况下，系统内纵波传播常数与频率的关系。可以发现，在通频带，两个方向传播的波数大小的绝对值及两个衰减常数均相等。表明应力纵波在两个方向上以相同的相速度传播，同时应力波在弧长坐标系的负方向上衰减。而在行波抑止带与抑止带，γ为纯虚数，意味着应力纵波在该频段不能以行波的形式在缆绳内传播。在行波抑止带，能观察到两列近场衰减波以不同的衰减系数向弧长坐标系的负方向衰减；在抑止带可以观察到向缆绳两个方向传播的近场快速衰减波。从图5中也可以发现，随着布放缆材料的cl逐渐增大，即随着布放缆弹性模量的增大和密度的减小，其行波截止频率也随之增大。并且随着频率ω的增大，各曲线的斜率均渐进趋向于张紧弦假设下的理论解γ=ω/c。

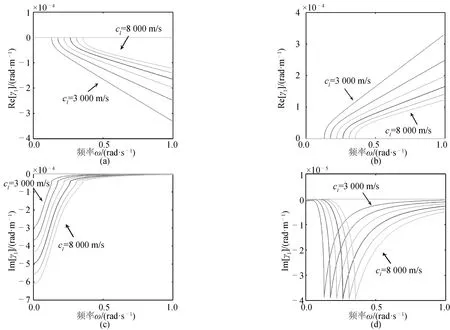
图5 布放缆内应力纵波频率关系曲线 (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)Fig.5 Frequency relation curves of longitudinal waves (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)

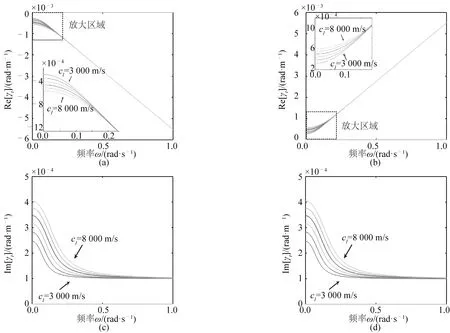
图6 布放缆内应力横波的频率关系曲线(3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)Fig.6 Frequency relation curves of transversal waves (opposite numbers of attenuation constants) are plotted (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)

图6展示了系统内横波的频率关系。与纵波不同的是，在所有频率下，应力横波均能够在缆绳系统内传播。相同频率下，应力横波的波数随着cl的增加而增加。在λ2→时，曲线渐进趋向于张紧弦假设下的理论波速的直线，即γ→ωct。在较低频率时，系统总体而言是色散的，其色散程度大小及色散频率区间随着cl的增加而增加。在cl→0或在高频时，系统的频率关系趋向于线性，系统逐渐趋向于非色散系统，该极限情况也与张紧弦理论解相符。

与Behbahani-Nejad M和 N C Perkins[8]通过将缆绳曲率与弧长坐标的关系线性化后计算得到的纯实数结果所不同的是，在保留非线性的情况下，应力横波的传播常数为复数，意味着在传播过程中其幅值会以相对应的衰减常数进行衰减，可以看到，随着频率的减小，其衰减常数随之增加，且在低频时，相同频率下的应力横波衰减常数随着cl的增加而增加。

3.3色散关系

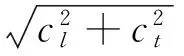
通过图7(c)、7(d)可以发现当频率大于行波截止频率时，两个相速度虚部相等，并且其幅值随着频率的减少而增大。而当频率小于行波截止频率时，系统有两种可能情况，如图4所示，如果ωcut_off是复数，则该频段属于抑止带，此时从图7(c)上可以看到一个相速度虚部在跨越截止频率时会从正值跳跃到负值，此时在抑止带可以观察到两列方向相反的近场衰减波；反之，如果ωcut_off为纯实数，图7(c)上的相速度并不会穿越零轴跳跃，此时该频段为行波抑止带，仅能观察到单一方向的衰减波，在该频段相速度的虚部会取到一个区域极大值，该极大值随着Im(ωcut_off)的绝对值的增加而减小，并随着布放缆的cl的减小而减小。另外从图7上同时可以看到，在λ1、λ2相同时，在相同频率，随着cl的减小，行波截止频率随之变小，抑止频带或半通频带所占的频率范围也随之减小。

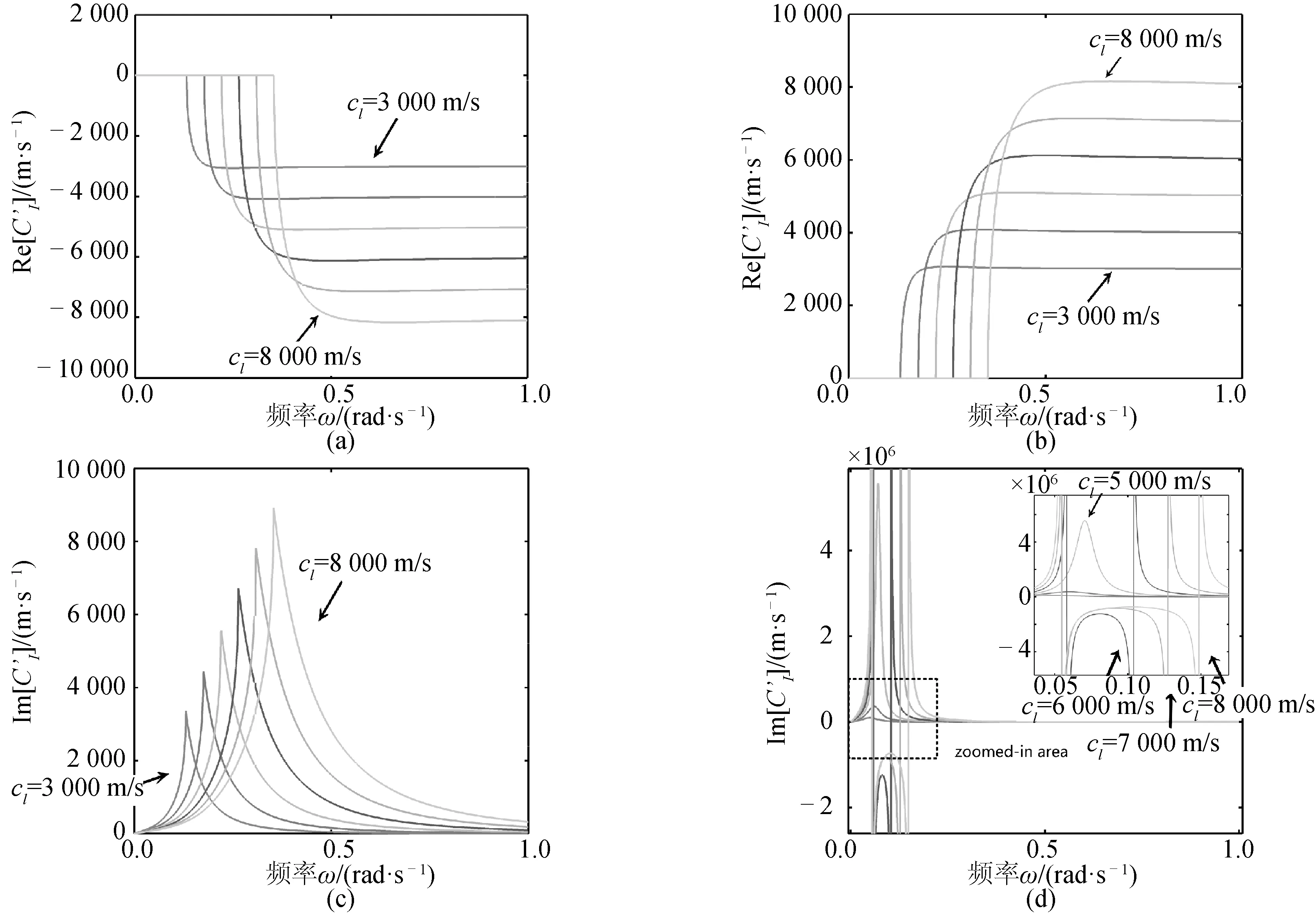
图7 布放缆内应力纵波色散关系 (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)Fig.7 Dispersion curves of longitudinal waves (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)

应力横波色散曲线如图8所示。横波在任何频率下均可以行波的形式传播。其相速度实部在0 Hz时为0 m/s，随后随着频率的增大而迅速增大，并渐进趋向于其渐进极限，即短波长/高频极限为±ct。该极限并不受缆绳属性cl的变化而变化，然而在中低频区，cl越大，应力横波的相速度则相对越小，更小的cl可使应力横波的相速度更快地趋向于其短波长/高频极限。

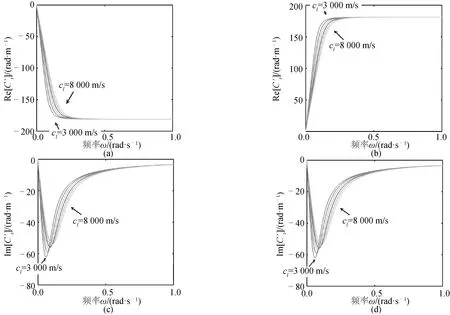
图8 布放缆内应力横波色散关系 (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)Fig.8 Dispersion curves of transversal waves (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)

3.4群速度

图9展示了纵波群速度与纵波相速度之比。

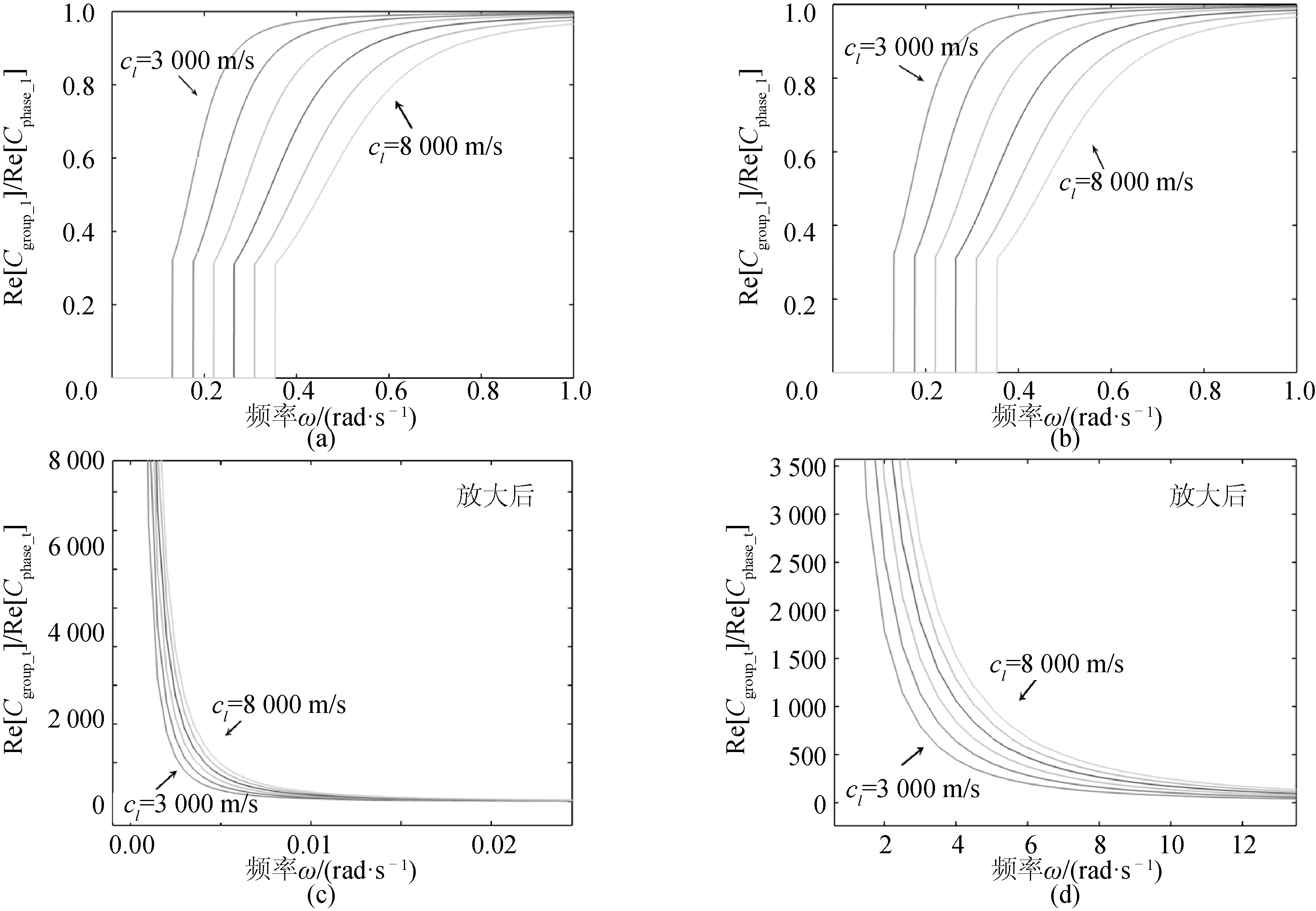
图9 布放缆内应力波群速度曲线 (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)Fig.9 Group velocity curves (3 000 m/s≤cl≤8 000 m/s,λ1=500 m,λ2=5 000 m)

由于只有位于通频带的应力纵波才能以行波的形式传播，因此在非通频带群时，纵波群速度与相速度都逼近0。由于被除数出现了接近于0的项，为了更好地展现通频带群速度特性，在图中仅展现通频带下的结果，非通频带下的该比例被设为0。

从图9(a)、9(b)中可以看到，当纵波的频率越过行波截止频率时，其迅速达到1/3左右，并迅速单调递增趋向于1。其表明，行波的群速度始终小于相速度，且在高频时两者趋向相等，在高频时可以认为系统是非色散的。

图9(c)、9(d)展示了横波的群速度相速度之比。在低频时，该比例非常高，随着频率的增加，该频率迅速降低并最终趋向于1。由于其比例始终大于1，因此横应力波的传播特性为反常色散，高频项会不断向波前锋聚集，最终在波前锋形成一个强间断波。随着波的传播，该前锋处的应力应变变化率将会变得很大，对布放缆产生巨大的加载。因此在设计和布放时需要对该点额外注意，需要增加系统安全系数以避免低估传播过程中逐渐集中的强间断波对布放缆的应力应变作用。

4 结 语

从应力波在缆绳中传播理论出发，研究了长布放缆系统中不同竖直张力下应力波的传播特性，并保留布放缆弧度与该点弧长坐标之间的非线性关系。研究表明：

1) 整个频域被两个截止频率与一个行波截止频率分成四个区域。从低频到高频分别为行波抑止带、抑止带、行波抑止带与通频带。

ⓐ 在通频带，应力纵波可以行波形式传播，且在传播时衰减，该系统为色散系统。

ⓑ 在行波抑止带，应力纵波不能以行波的形式向外传播。但是在应力突变源附近会产生双向的近场衰减波。

ⓒ 在抑止带，应力纵波不能以行波的形式向外传播。但是在应力突变源附近会产生单向的近场衰减波。

ⓓ 应力横波始终能够以行波的形式向外传播，不存在抑止带。系统在考虑了布放缆弧度与该点弧长坐标之间的非线性关系时为色散系统。

2) 应力横波与纵波的行波群速度在高频时趋向于它们的相速度。然而应力横波表现出了反常色散特性，因此高频项会在传播的过程中向波前锋聚集，从而形成前间断波，该点在进行布放缆设计考虑时特别需要留意。

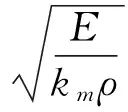
ⓐ 布放缆内传播的应力纵波较大的截止频率与行波截止频率均随着cl的增大而增大，而较小的截止频率在其内部竖直张力较大时也随着cl的增大而增大。

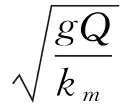
ⓒ 值得注意的是，布放缆中应力横波的波数随着cl的增加而增加，该效应在较低频率时更为显著；且在中低频区，随着cl增大，应力横波的相速度则相对减小，更小的cl可使应力横波的相速度更快地趋向于短波长/高频极限。

ⓓ 随着cl的增加，应力纵波的群速度与相速度之比随之下降，而应力横波的群速度与相速度之比随之增加。

[1] 蒋凯辉.防风系船水鼓系列研究[D].天津:天津大学,2005.(JIANG K H.Study of buoy mooring system [D].Tianjin:Tianjin University,2005.(in Chinese))

[2] PLAUT R H,ARCHILLA J C,MAYS T W.Snap loads in mooring lines during large three-dimensional motions of a cylinder [J].Nonlinear Dynamics,2000,23(3):271-284.

[3] WANG L L.Foundations of stress waves [M].Amsterdam: Elsevier,2007.

[4] POISSON S D.Mémoire Sur l’Équilibre et le Mouvement des Corps Elastique,in: Memorandum on Equilibriums and the Movement of Elastic Bodies,vol.8,Mémoires de l'Académie des Sciences de l'Institut de France [M].Paris : L’imprimerie de Firmin Didot Freres,1845,357-570.

[5] CAUCHY A.Exercises de mathématiques [M].Paris : Jean Spurny,1828.

[6] GRAFF K F.Wave motion in elastic solids [M].New York: Dover Publications,1991.

[7] BEHBAHANI-NEJAD M,PERKINS N C.Freely propagating waves in elastic cables[J].Journal of Sound & Vibration,1996,196(2):189-202.

[8] BEHBAHANI-NEJAD M,PERKINS N C.Harmonically forced wave propagation in elastic cables with small curvature[J].Journal of Vibration & Acoustics,1997,119(3).

[9] KIM W J,PERKINS N C.Linear vibration characteristics of cable-buoy systems[J].Journal of Sound & Vibration,2002,252(3):443-456.

[10] KIM W J,PERKINS N C.Coupled slow and fast dynamics of flow excited elastic cable systems[J].Journal of Vibration & Acoustics,2003.

[11] ZHANG S X,TANG Y G,HOU S J,et al.Characteristic analysis of stress wave in mooring line in taut-slack condition[J].Engineering Mechanics,2010,27(5):53-59.

[12] ABEDINNASAB M H,HUSSEIN M I.Wave dispersion under finite deformation[J].Wave Motion,2012,50(3):374-388.

[13] ABEDINNASAB M H,HUSSEIN M I.Analysis of elastic wave propagation in nonlinear beams[C]// ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.2011:207-212.

[14] BEZVERKHII A I,KORNIENKO V F,SHUL'GA N A.Forced spatial vibrations of anchor cable systems[J].International Applied Mechanics,2001,37(9):1 222-1 228.

[15] N A SHUL’GA,A I BEZVERKHII.Dynamics of deformable flexible systems in liquid[J].International Applied Mechanics,2007,43(8):829-848.

[16] BEZVERKHII A I,KORNIENKO V F,SHUL'GA N A.The viscoelastic effect of the cable on the dynamics of an underwater towed system suspended from a buoy[J].International Applied Mechanics,2001,37(8):1 055-1 061.

[17] SHUL'GA N A,BEZVERKHII A I.Dynamics of branched continuous-discrete systems towed in rough water[J].International Applied Mechanics,2005,41(10):1 156-1 160.

[18] BEZVERKHII A I.Dynamics of towed branched underwater system with support buoy under rough water[J].International Applied Mechanics,1999,35(4):426-430.

[19] PERKINS N C,MOTE C D.Three-dimensional vibration of travelling elastic cables[J].Journal of Sound & Vibration,1987,114(2):325-340.

[20] FRAZER I,PERINET D,VENNEMANN O,et al.Technology required for the installation of production facilities in 10,000 ft of water[C]//Proceedings of the Offshore Technology Conference,2005.Http://doi.org/10.4043/17317-MS.

Study of characteristics of stress waves propagating freely in deep-sea deployment cables with different cable properties

WU Chenghao,YANG Jianmin,TIAN Xinliang,HU Zhihuan,PENG Tao

(Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,State Key Lab.of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

The spectral responses of stress waves freely propagating along deep-sea deployment cables are investigated using an analytical method.Hamilton’s Principle is used for the modeling of the deployment system.The curvature of the cable is considered and both transversal and longitudinal propagating waves are taken into consideration.The relation between cable curvature and cable arc coordinate is kept nonlinear.The influence of cable’s property and the vertical stress inside cable on the characteristics of stress waves propagating freely in deep-sea deployment cable is calculated.Calculation shows that those factors have a great influence on two stress waves’ frequency,dispersion relations as well as phase velocities and group velocities.For longitudinal stress waves,four distinct frequency bands are identified by two cut-off frequencies and one pass-band-edge frequency.Partly-pass band and stop band exist at low frequencies.Longitudinal stress wave can only propagate in pass-band,however transversal stress waves may propagate at any frequency.

stress wave; deep-sea deployment; slack-taut; snap tension

P751

A

10.16483/j.issn.1005-9865.2017.05.002

1005-9865(2017)05-0012-11

2016-10-17

国家重点研发计划支持“深海多金属结核采矿试验工程”资助项目(2016YFC0304100)；国家自然科学基金支持资助项目(51239007，51509152，11632011)

吴丞昊(1992-)，男，硕士研究生，主要从事深海采矿水动力学特性及布放系统中应力波传播研究。E-mail: Chenghao.wu@sjtu.edu.cn

杨建民。E-mail: jmyang@sjtu.edu.cn