绷紧式系泊缆冲击张力特性研究

张火明，谢 卓，方贵盛，孔令滨

(1.中国计量大学 浙江流量计量技术重点实验室，浙江 杭州 310018; 2.浙江水利水电学院 机械与汽车工程学院，浙江 杭州 310018)

绷紧式系泊缆冲击张力特性研究

张火明1，谢 卓1，方贵盛2，孔令滨1

(1.中国计量大学 浙江流量计量技术重点实验室，浙江 杭州 310018; 2.浙江水利水电学院 机械与汽车工程学院，浙江 杭州 310018)

采用集中质量法研究了绷紧式系泊系统中系缆由于松弛-张紧过程产生的冲击张力。建立系泊缆绳离散的集中质量模型，对其独立单元进行受力分析并建立了单元的运动方程。给定缆绳上端点简谐激励，通过Ansys中的Aqwa模块，分析了缆绳的运动响应；针对缆绳运动响应过程中的三种状态进行了模拟计算，探讨了冲击张力产生的条件；研究了缆绳初始预张力、上端点激励幅值和频率、拖曳力系数、弹性模量以及单位长度质量对动态张力的影响。研究结果表明：这些影响因素不仅会影响缆绳动态张力的大小，也会对缆绳中的冲击张力产生一定的影响。

绷紧式系泊缆；运动响应；冲击张力

近年来，新型绷紧式系泊系统凭借其在深水应用中的优越表现而倍受关注。在系泊系统运动响应过程中，当浮体运动幅值超过某一临界值时，缆绳可能会表现出零张力和最大值张力，即出现了缆绳冲击现象。缆绳发生冲击现象时产生的力通常比简单的动态载荷大很多，这会对缆索结构造成很大的破坏，严重影响系泊系统的使用寿命。因此对系泊缆绳冲击张力特性的研究就显得十分重要。

Plaut等[1-2]研究发现当浮体的运动幅度很大时，缆绳就会松弛，一旦再次张紧，就会出现很大的动态张力，此时能量会有损失。Dracos和Huang[3]通过试验研究发现缆绳在张紧状态时，张力以激振频率变化，但是一旦发生松弛-张紧现象，就会在张力中出现高频分量。Huang[4]通过研究发现，缆绳在松弛状态下，会发生几何形状的改变；张紧状态，缆绳则表现出单纯的弹性载荷模式；松弛-张紧状态，缆绳跨越了从几何构型到弹性变形的过程。刘敏[5]以简化的系泊系统力学模型为对象，研究了在激振力不同初始条件下系泊缆绳的非线性动力学特性。赵景瑞[6]依据集中质量法建立系泊缆绳柔性力学模型，研究了各种因素对于缆绳动态张力与水中构型的影响程度。唐友刚[7]考虑到缆绳所具有的粘-弹特性，对深海平台系泊系统松弛-张紧引起的冲击载荷进行了研究。张素侠[8]采用应力波的方法对深海系泊系统松弛-张紧过程的冲击张力进行了研究。曹阳，张素侠等[9-10]对系泊缆绳的冲击载荷进行了实验研究，通过对比分析的方法，研究了不同因素对缆绳张力带来的影响并探讨了缆绳发生冲击张力的判别方法。研究后得出冲击载荷发生的重要特征为：历程张力曲线变得陡峭、张力值急剧增大以及张力中出现多倍响应频率成分。

本文借助Ansys中的Aqwa模块，针对缆绳运动响应过程中的三种状态进行了模拟计算；研究了缆绳初始预张力、上端点激励幅值和频率、拖曳力系数以及弹性模量对动态张力的影响。

1 数值模拟

1.1模型建立

图1 缆绳离散集中质量模型Fig.1 Discrete mass model of the cable

图2 缆绳单元受力分析Fig.2 Force analysis of cable

1.2运动方程

图2显示了细长圆环型缆绳单元的受力情况。作用于缆绳单元的外力主要包括流体水动力载荷以及惯性载荷。在缆绳动态分析中不考虑扭转变形。此缆绳单元的运动方程如下：

缆绳的弯矩和张力分别与其弯曲刚度和轴向刚度有关，其关系如下：

式中：I为截面关于中性轴的惯性矩，ε为单元轴向应力。

为确保方程(1)～(4)的唯一解，在顶部和底部两端施加固定的连接边界条件：

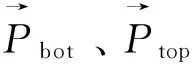
为了求解缆绳速度和位置的估计加速度值，采用两阶段预测-校正算法。第一阶段为预测阶段，首先要计算出总的作用力，往往是已知时间、位置、速度的函数；然后对在t+dt时刻的速度和位置进行预测。第二阶段为校正阶段，求出在t+dt时刻的总作用力值以及加速度值；利用泰勒定理计算t+dt时刻修正后的速度和位置。

2 缆绳动力响应结果及分析

选取的缆绳参数如表1所示。

表1 缆绳参数表Tab.1 Parameters of cable

2.1缆绳运动响应分析

缆绳参数如表1所示，给定缆绳上端点激励为正弦激励，激励幅值Ap=5 m，激励频率f=1 rad/s，设定锚系点为坐标原点，沿缆绳方向为正方向，选取缆绳500 m和1 500 m处，对其进行计算，得到不同方向的时域位移历程曲线以及运动轨迹曲线，如图3和图4所示。

图3 缆绳1 500 m处运动轨迹Fig.3 The trajectories of cable at 1 500 m

图4 缆绳500 m处运动轨迹Fig.4 The trajectories of cable at 500 m

从图3和图4中可以看到，虽然缆绳上端点仅仅是沿x轴方向进行激励，但是缆绳在x轴，y轴，z轴方向均产生运动响应，且缆绳初期的运动轨迹分布比较松散，这说明初期运动不稳定；但经过一段时间后，运动轨迹逐渐趋于密集甚至重合，这说明缆绳运动会达到稳定状态，最终将沿某一特定轨迹运动。

2.2缆绳张力分布

缆绳的最大张力值对缆绳的研究具有重要意义，对缆绳各部分的张力值进行计算，以确定各段缆绳的张力情况。取缆绳质量为89.43 kg/m，上端激励幅值为5 m，激励频率为1 rad/s。对100 s内缆绳各段张力进行计算，得到各段缆绳张力的最大值如图5所示。从图中可以看出，缆绳两端的张力最大值较大，其中顶端略大于底部张力值，中间部分较小， 在1 000 m左右达到最小值。

图5 缆绳前100 s各段张力最大值Fig.5 The maximum value of the tension

3 缆绳冲击张力特性研究

3.1冲击张力产生条件

缆绳的运动过程分为三种状态，分别是：松弛状态，松弛-张紧状态和张紧状态。为研究冲击张力产生条件，分别针对三种状态下缆绳的动态张力进行研究。缆绳锚系点以及上端导缆点固定，固定距离为2 123 m。文中通过改变设置缆绳的长度，以达到缆绳在三种状态下运动的条件。

1)松弛状态下缆绳动态张力

设置缆绳长度为2 140 m，此时缆绳初始预张力为1.561E6 N，给定上端点激励幅值为0.5 m，分别采用线性方法和非线性方法进行计算，其中非线性方法主要考虑非线性刚度，得到缆绳的线性和非线性张力如图6所示。从图6中可以观察到，缆绳的非线性张力要稍大于线性张力。动态张力曲线随时间呈正弦曲线变化，过程中并没有冲击张力的产生。

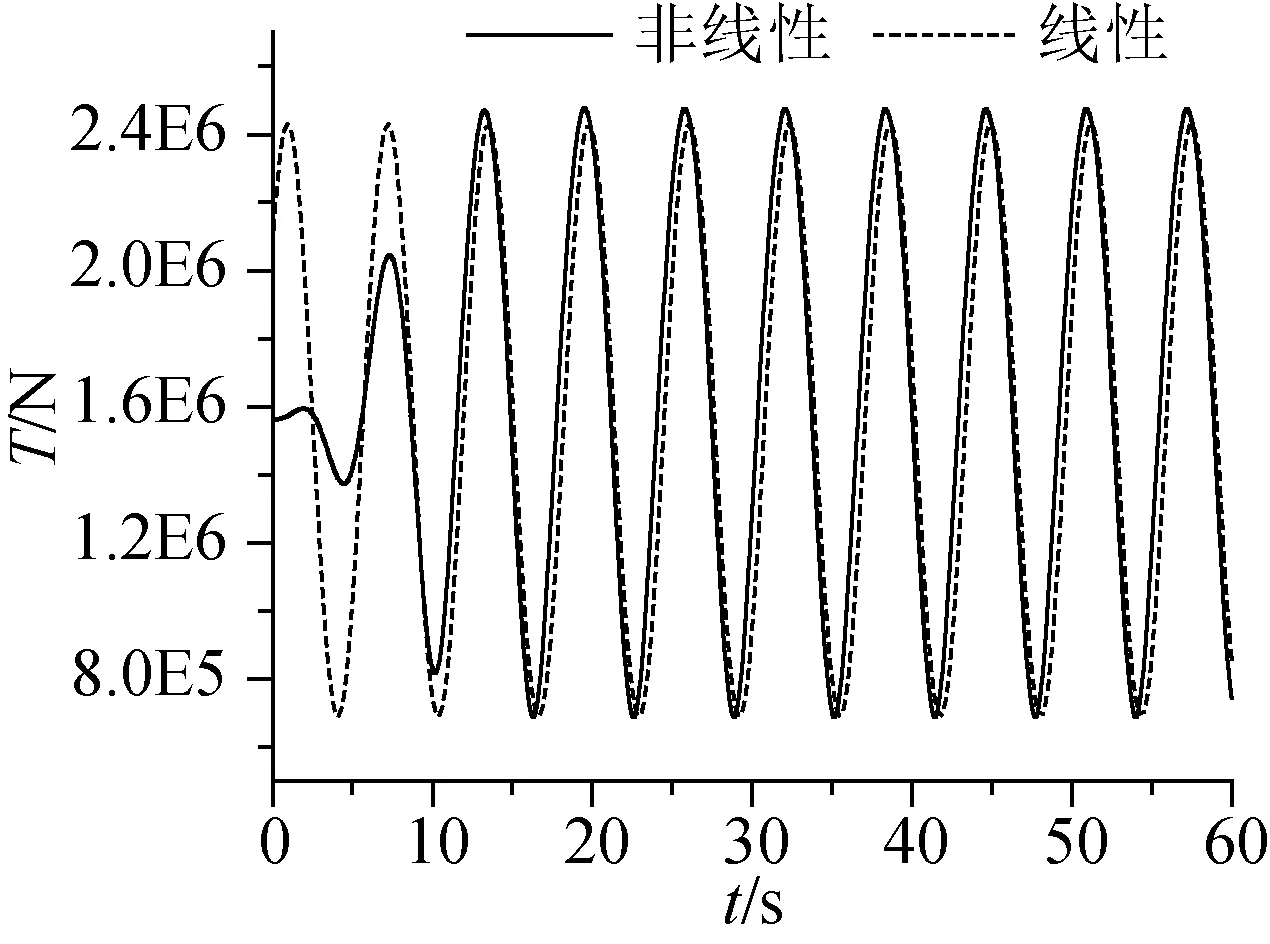
图6 松弛状态缆绳张力曲线Fig.6 The cable tension curve in the relaxed state

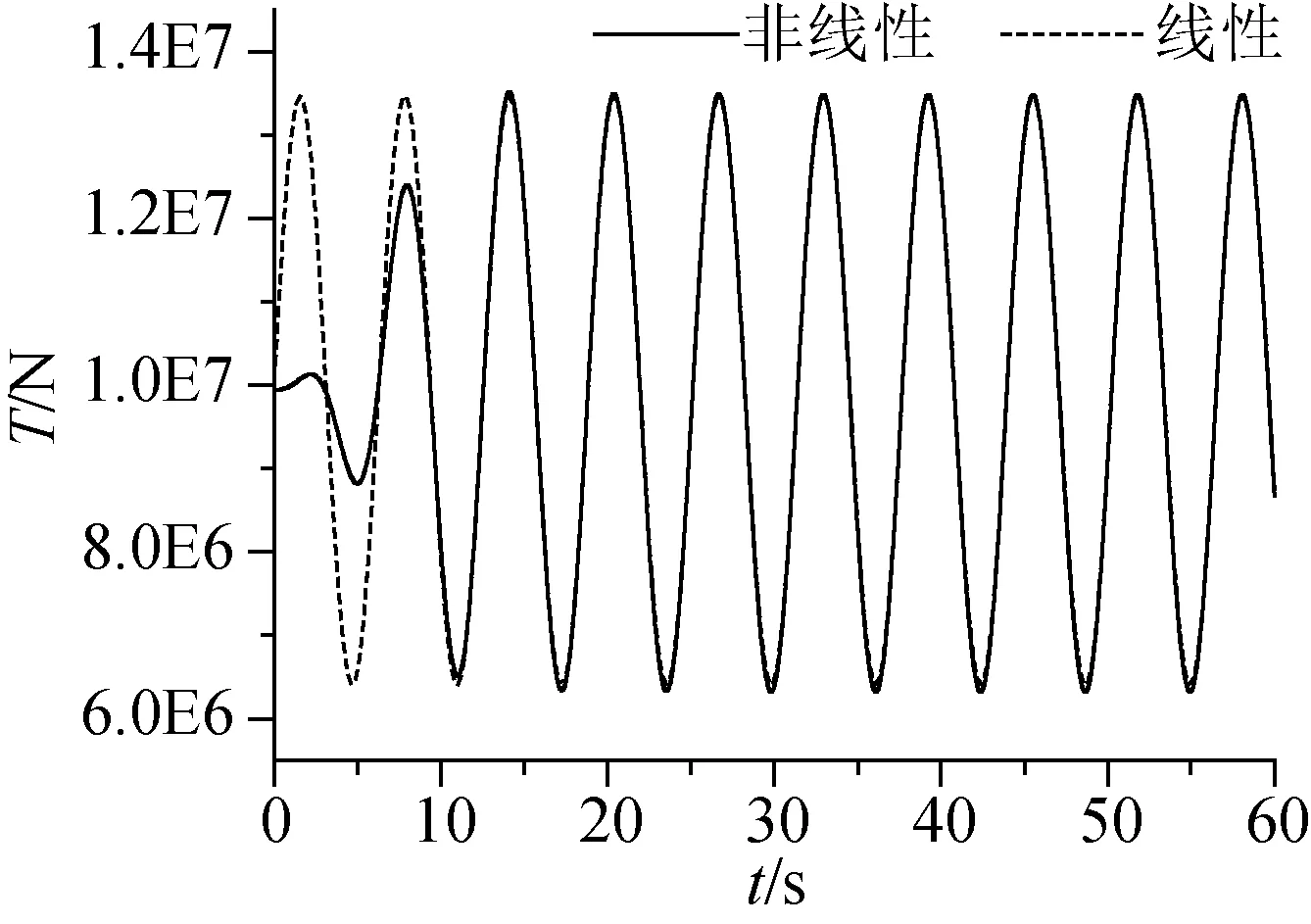
图7 张紧状态缆绳张力曲线Fig.7 The cable tension curve in the tightened state

2)张紧状态下缆绳动态张力

设置缆绳长度为2 120 m，此时缆绳处于绷紧状态，缆绳初始预张力为6.524E6 N，给定缆绳上端点激励幅值为2 m，缆绳运动过程中将一直处于绷紧状态。计算得到缆绳的线性和非线性动态张力曲线如图7所示。从两条曲线对比可以看出，在张紧状态下，除前10 s，两种方法计算得到的动态张力曲线基本重合。

3)松弛-张紧状态缆绳动态张力

参数如同张紧状态时，增大上端点激励幅值，缆绳运动过程中将会经历松弛-张紧状态。采用线性与非线性方法计算得到缆绳的动态张力曲线如图8所示。采用非线性方法计算得到的动态张力曲线中，出现了许多突变的尖峰，且不同于松弛和张紧状态，张力中出现负张力值。与线性张力曲线相比，非线性张力的峰值要远大于线性张力的峰值。图9为线性和非线性张力的频率成分图。张力的频率成分中除了激励频率f=1.0 rad/s成分外，还出现了f=2.0、3.0、4.0、5.0和6.0 rad/s的频率成分，由此可知系统内可能发生了2倍、3倍、4倍甚至5倍的超谐共振。

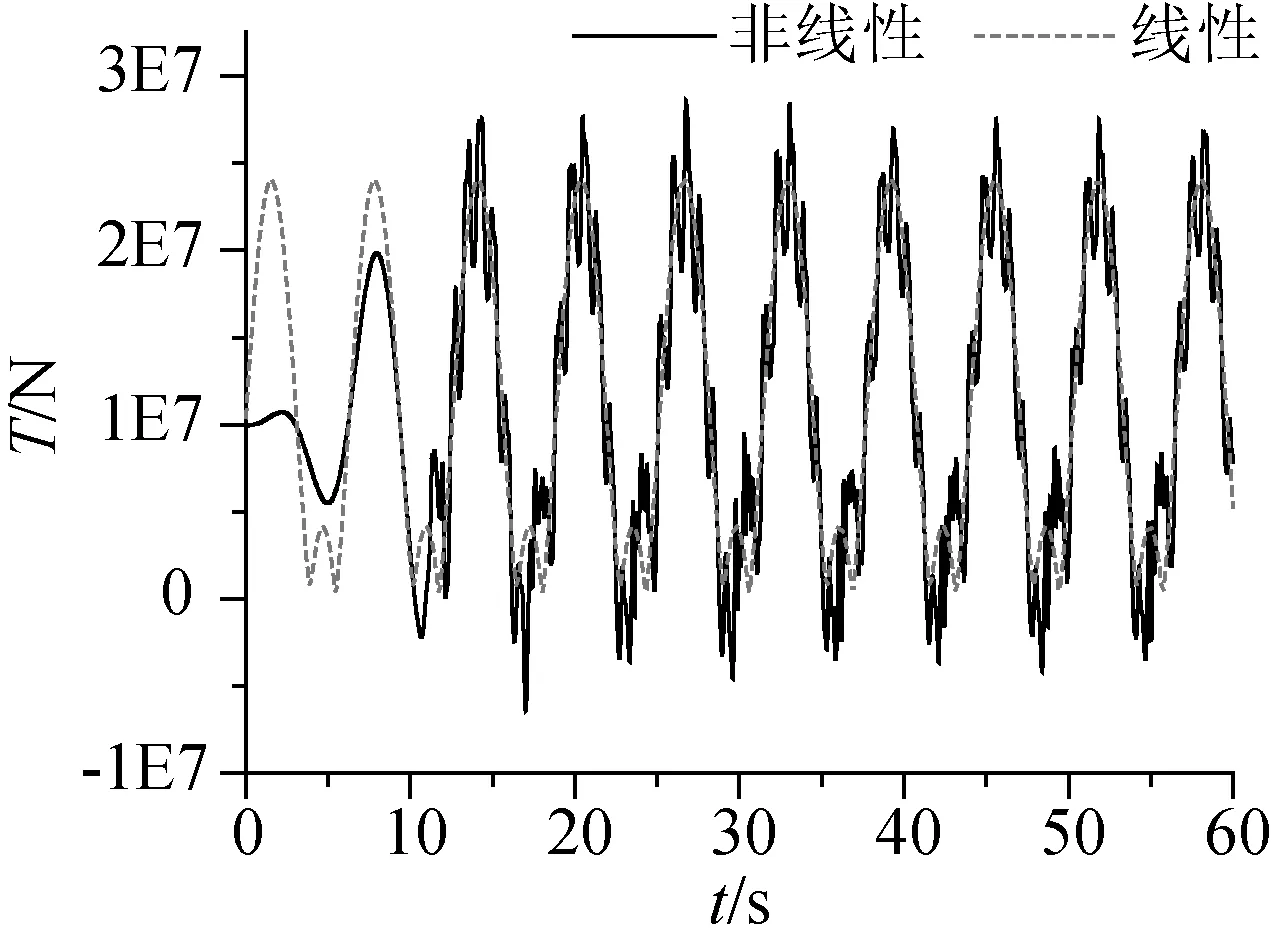
图8 线性和非线性动态张力曲线Fig.8 Linear and nonlinear dynamic tension curve

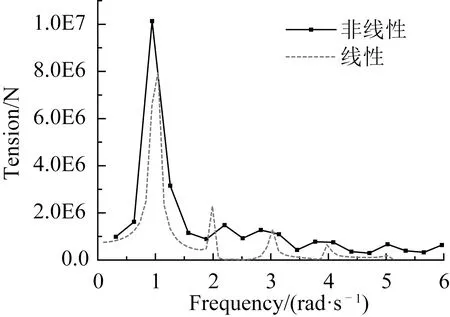
图9 频率成分Fig.9 Frequency component diagram

3.2不同因素对缆绳动态张力影响

1)初始预张力对缆绳动态张力影响

图10 初始预张力与动态张力关系Fig.10 The relation between pre-tension and dynamic tension

取激励幅值A=10 m，激励频率f=1 rad/s，缆绳弹性模量E=1E9 N/m2，计算得到缆绳动态张力与初始预张力曲线，采用四阶多项式进行拟合，拟合系数分别为：B1=-1.387 55，B2=6.386 91E-7，B3=-6.375 12E-14，B4=2.013 04E-21，如图10所示。缆绳的动态张力与预张力的关系曲线呈非线性上升趋势，随着预张力的增大，缆绳的张力最大值也逐渐增大。

2)拖曳阻力系数对缆绳张力影响

在缆绳的运动方程中，流体产生的拖曳力，是造成系统非线性的主要因素之一。研究流体拖曳力对缆绳动态张力的影响，取上端点激励幅值Ap=5 m，频率f=1 rad/s，纵向拖曳力系数Cd2=0.025。

图11 不同横向阻尼缆绳动态张力曲线Fig.11 The dynamic tension curves of different transverse drag coefficients

计算不同横向拖曳力系数时，缆绳动态张力曲线如图11所示，图12是横向阻尼与缆绳张力最大值的四阶拟合曲线，拟合系数分别为B1=-8.931 82E6，B2=1.512 02E7，B3=-8.282 34E6，B4=1.475 09E6。

从图11中可以看到横向阻尼为1.6和1.4时，张力中的突变现象明显少于横向阻尼为0.4和1.6时。即随着横向阻尼的逐渐增大，缆绳中张力的突变现象逐渐减少。图12中的横向阻尼与张力的最小二乘法拟合曲线整体呈勺状，且缆绳在横向阻尼为0.4～0.5之间张力达到最小。

图12 横向阻尼与缆绳张力关系曲线Fig.12 The relation between transverse drag and cable tension

图13 动态张力与纵向阻尼系数关系曲线Fig.13 The relation between inline drag and tension

设定横向阻尼系数Cd1=1.25,计算不同纵向阻尼下缆绳的张力曲线，结果如图14所示。从图14中观察到：纵向阻尼系数为0.05、 0.15时，张力曲线中突变现象出现较多；纵向阻尼系数为0.25、0.3时，张力曲线中的突变现象出现较少。随着纵向阻尼系数的增大，与横向阻尼一样，张力中的突变现象也逐渐减少。图13为纵向阻尼系数与缆绳张力的拟合曲线。与横向阻尼不同，曲线整体呈下滑趋势，随着纵向阻尼系数的增加，缆绳中最大张力值逐渐下降。

图14 不同纵向阻尼时缆绳动态张力曲线Fig.14 The dynamic tension curve under different inline drag coefficent

3)激励幅值对缆绳张力的影响

缆绳弹性模量E=1E11N/m2，激励频率f=1 rad/s，,取上端点激励幅值A分别为3、4、5及6 m时，计算得到缆绳顶端的动态张力曲线如图15所示。图16为激励幅值与缆绳张力的关系曲线，其中对幅值A小于4 m部分，采用线性拟合，斜率为1 992.27；对幅值大于4 m部分采用四阶多项式进行拟合，拟合系数分别为B1=-288 878.58,B2=89 046.97，B3=-11 888.43,B4=585.60。

由图15可以看到，在上端点激励幅值为3 m和4 m时，缆绳顶端张力呈正弦规则变化，没有出现突变现象。由此可知，此情况下不存在冲击张力。这是由于激励幅值为3 m、4 m时，上端点的运动不足以使缆绳恢复到松弛状态，缆绳一直处于张紧状态，不存在从松弛到张紧的转变过程。当激励幅值大于5 m时，缆绳存在从松弛到张紧的转变过程，缆绳张力产生明显的突变现象。由图16可以看出，当激励幅值小于4 m时，缆绳的动态张力随激励幅值呈线性增大；当激励幅值大于5 m时，缆绳动态张力则随激励幅值呈非线性增大。

图15 不同幅值激励下缆绳张力曲线Fig.15 The tension curves of different amplitude under the excitation of the cable

图16 激励幅值与张力关系Fig.16 The relation curve between excitation amplitude and tension

图17 不同频率下缆绳张力曲线Fig.17 The cable tension curve under different frequencies

图18 动态张力与激励频率关系Fig.18 The relation between tension and excitation frequencies

4)激励频率对缆绳张力的影响

缆绳弹性模量E=1E11N/m2，上端点激励幅值A为5 m，取激励频率f分别为0.6、1.0、1.4和1.8 rad/s时，计算得到缆绳顶端的动态张力曲线如图17所示。图18为缆绳最大张力与激励频率关系图。

从图17可以看出：不同频率下，缆绳从松弛到张紧转变过程中均会产生冲击张力；但是频率较低时，张力曲线产生少量的突变现象，冲击不明显也不够剧烈；频率较大时，张力曲线产生大量的突变现象，冲击比较明显而剧烈。从图18观察得出：缆绳的动态张力随激励频率的增加而呈非线性增加。

综上所述，假设缆绳上端点为正弦激励，缆绳的最大动态张力随激励幅值的增大而增大，随频率的增大而增大。这也印证了张素侠[8]的推断：缆绳的最大动态张力可能与上端点的运动速度有关，运动速度越大，其最大动态张力也越大。

5) 弹性模量对缆绳张力影响

取上端点激励幅值A为5 m，激励频率f为1 rad/s时，计算得到不同弹性模量下缆绳顶端的动态张力曲线，如图19所示。

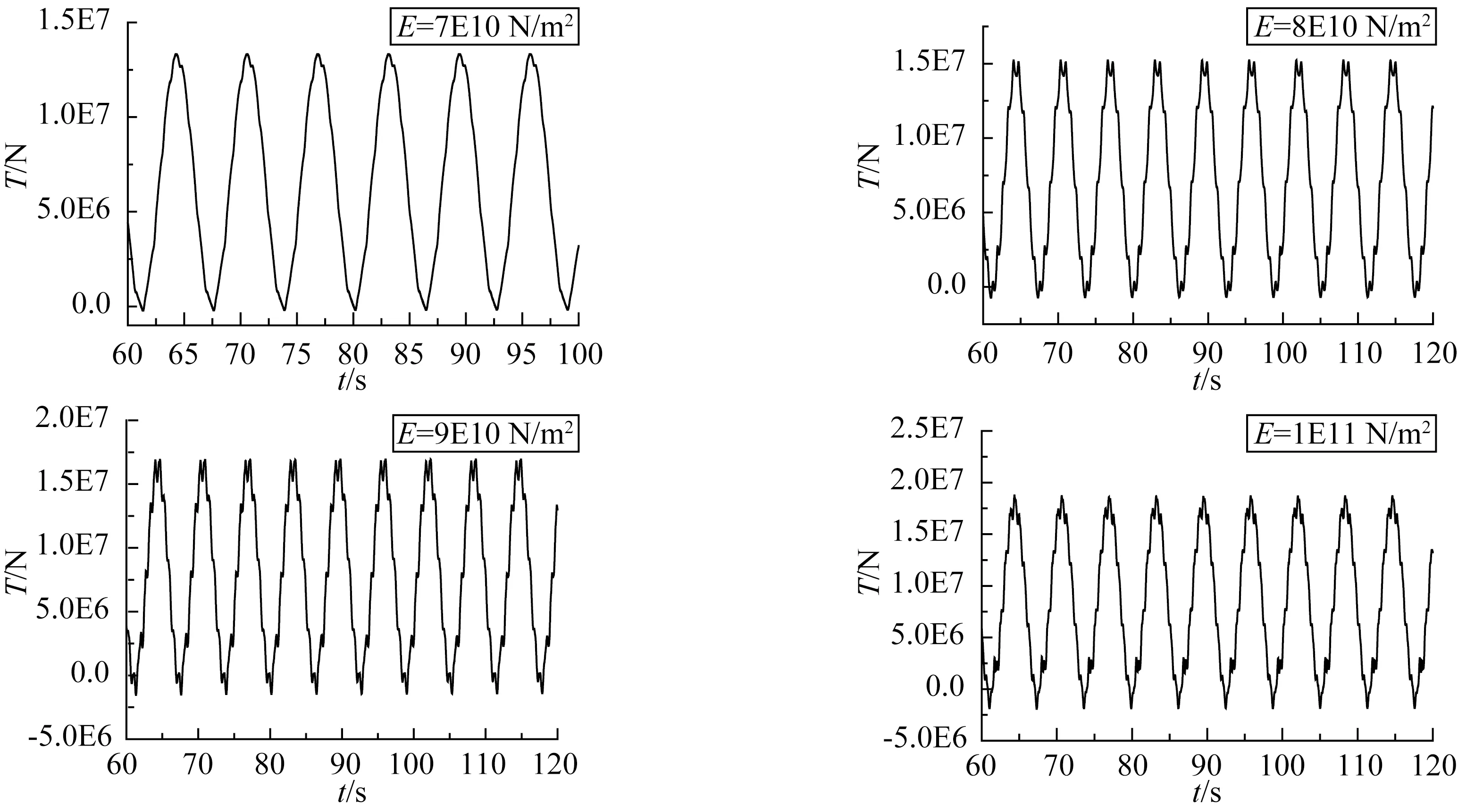
图19 不同弹性模量缆绳动态张力Fig.19 The dynamic tension curves of different elastic modulus of the cable

可以看到，当弹性模量小于8E10 N/m2时，缆绳动态张力呈正弦变化，并未产生突变现象，其动态张力也未出现负值，此时不存在冲击张力。当弹性模量大于8E10 N/m2时，缆绳的动态张力中出现比较明显的突变现象。图20为弹性模量与张力关系拟合曲线，E≤7E10 N/m2部分采用线性拟合，斜率为1.692 11E-4，缆绳中张力最大值随弹性模量成线性增大；E≥8E10 N/m2部分采用4阶多项式拟合，动态张力最大值与弹性模量则呈非线性上升趋势。

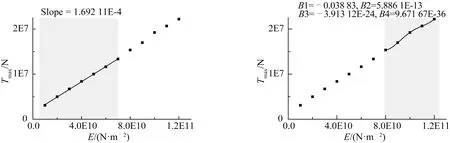
图20 张力最大值与弹性模量关系Fig.20 The relation between the maximum tension and elastic modulus

3.3冲击放大系数

冲击放大系数表示系缆的最大动态张力与静态张力的比值。以质量作为影响因素，研究不同质量系缆绳动态张力的冲击放大系数。给定缆绳上端点激励幅值为5 m，激励频率为1 rad/s，计算不同质量下缆绳的动态张力，计算结果如图21所示。

图21 不同质量时缆绳的动态张力Fig.21 The dynamic tension cable of different qualities

图22 冲击放大系数Fig.22 The impact of amplification factor

图21研究了质量为48～168 kg/m时缆绳的动态张力，发现质量为68、88、108和128 kg/m时，动态张力中出现严重的冲击载荷现象。 质量为28、48、148和168 kg/m时，动态张力则呈现平滑曲线，并无冲击现象。这说明只有缆绳密度与海水密度相近时才会产生冲击张力。进一步求得冲击放大系数，结果如图22所示。

由图中看到，缆绳的冲击放大系数在88 kg/m时最大，缆绳发生冲击载荷时， 最大动态张力与静态张力的比值要大于未发生冲击载荷时的值。

4 结 语

通过对缆绳动态张力可能造成影响的几种因素进行研究后发现，缆绳的动态张力最大值随着初始预张力、弹性模量以及缆绳上端点激励幅值和频率的增大而增大；缆绳动态张力最大值在横向拖曳力系数位于0.4～0.5之间达到最小，且随着纵向拖曳力系数的增大而减小。这些影响因素不仅会影响缆绳动态张力的大小，也会对缆绳中的冲击张力产生一定的影响。横向阻尼越小，纵向阻尼越大，频率越高，动态张力中突变发生越频繁。需要特别指出的是，最后以单位质量为例对缆绳的冲击张力展开研究，发现只有缆绳密度与海水密度相近时才会产生冲击张力，且发生冲击张力时的冲击放大系数要大于未发生冲击张力时的情况。

[1] PLAUT R H.Snapping-cable energy dissipater(SCED)for reducing seismic damage to structures[M].NSF Proposal,2001.

[2] PLAUT R H,ARCHILLA J C,MAYS T W.Snap loads in mooring lines during large three-dimensional motions of a cylinder[J].Nonlinear Dynamics,2000,23(3): 271-284.

[3] VASSALOS D,HUANG S,KOUROUKLIS A.Experimental investigation of snap loading of marine cables[C]//The Fourteenth International Offshore and Polar Engineering Conference.International Society of Offshore and Polar Engineers,2004.

[4] PASCOAL R,HUANG S,BARLTROP N.Assessment of the effect of mooring systems on the horizontal motions with an equivalent force to model[J].Ocean Engineering,2006,33(11): 1 644-1 668.

[5] 刘敏.海洋平台系泊缆绳非线性动力学特性研究[D].镇江: 江苏科技大学,2015.(LIU Min.Study on nonlinear dynamic characteristics of mooring lines of offshore platform[D].Zhenjiang: Jiangsu University of Science and Technology,2015.(in Chinese))

[6] 赵晶瑞,范模,段梦兰.深水系泊缆绳动力响应研究[J].船舶工程,2013(4):103-107.(ZHAO Jingrui,FAN Mo,DUAN Menglan.Study on dynamic response of deepwater mooring line[J].Ship engineering,2013 (4): 103-107.(in Chinese))

[7] 唐友刚,张素侠,张海燕,等.系泊系统松弛-张紧引起的冲击张力研究[J].振动与冲击,2008,27(4):70-72.(TANG Yougang,ZHANG Suxia,ZHANG Haiyan,et al.Study on the impact tension of mooring system relaxation tension strain [J].Vibration and shock,2008,27(4):70-72.(in Chinese))

[8] 张素侠.深海系泊系统松弛-张紧过程缆绳的冲击张力研究[D].天津: 天津大学,2008.(ZHANG Suxia.Study on the impact of tension of mooring system in deep sea cable tension relaxation process[D].Tianjin: Tianjin University,2008.(in Chinese))

[9] 曹阳.深水系泊缆绳冲击载荷实验研究[D].天津: 天津大学,2009.(CAO Yang.Experimental study on load impact of deepwater mooring cable[D].Tianjin: Tianjin University,2009.(in Chinese))

[10] 张素侠,唐友刚,林维学,等.水下缆绳松弛-张紧过程的冲击张力实验研究[J].中国造船,2008,49(A02):385-390.(ZHANG Suxia,TANG Yougang,LIN Weixue,et al.Experimental study on the impact of underwater cable tension in taut slack process[J].Shipbuilding of China,2008,49 (A02): 385-390.(in Chinese))

Investigation on the impact tension characteristics of taut mooring lines

ZHANG Huoming1,XIE Zhuo1,FANG Guisheng2,KONG Lingbin1

(1.Zhejiang Provincial Key Laboratory of Flow Measurement Technology,China Jiliang University,Hangzhou 310018,China; 2.Mechanical and Automotive Engineering College,Zhejiang Water Conservancy and Hydropower College,Hangzhou 310018,China)

The impact force caused by the relaxation tension of the mooring line in the taut mooring system is studied by used of the method of lumped mass.Mooring lines discrete lumped mass model is established,the stress is analyzed and the equation of motion for the independent unit is established.Given cable endpoint harmonic excitation,through ANSYS/Aqwa,the response of cable movement is analyzed; the cable motion response process in three states is simulated and the impact tension conditions are discussed; and the initial cable tension,upper point excitation amplitude and frequency,drag effect of drag coefficient,elastic modulus and mass per unit length of dynamic tension are studied.The results show that these factors will not only affect the dynamic cable tension,but also have some influence on the impact load of cable.

taut mooring line; motion response; impact tension

P751

A

10.16483/j.issn.1005-9865.2017.05.003

1005-9865(2017)05-0023-10

2016-09-02

浙江省自然科学基金项目(Y14E090034,Y13F020140)；浙江省青年科学家培养计划项目(2013R60G7160040)；上海交通大学海洋工程国家重点实验室开放基金项目(1516)；卫星海洋环境动力学国家重点实验室开放基金项目(SOED1706)

张火明(1976-)，男，湖北武穴人，博士后，副教授，主要研究领域为海洋工程流体力学。E-mail:zhm102018@163.com