楔形体在波浪中自由入水的数值模拟

王 平，袁 帅，张宁川，陈伟斌，陈 元

(1.国家海洋环境监测中心，辽宁 大连 116023; 2.大连理工大学 海岸及近海工程实验室，辽宁 大连 116024)

楔形体在波浪中自由入水的数值模拟

王 平1，袁 帅1，张宁川2，陈伟斌1，陈 元1

(1.国家海洋环境监测中心，辽宁 大连 116023; 2.大连理工大学 海岸及近海工程实验室，辽宁 大连 116024)

物体入水时波浪的影响不可忽略，基于流体力学模型采用VOF法，并利用自定义函数，模拟了楔形体的自由入水过程；同时结合推波板原理及海绵层消波理论实现了数值水槽的造消波，完成了波浪中楔形体自由入水的模拟，计算了楔形体入水时所受的水作用力、自由液面变化及物面压强分布等，研究了不同波高、周期以及在波浪不同位置入水时对楔形体的影响。结果表明：本文建立的数值模型可很好地模拟楔形体入水造成的射流及空泡的形成发展过程，波浪对楔形体入水的影响主要由波浪内部流场变化及表面波形决定，在波浪不同位置处入水对楔形体受力及入水形态均有较大影响。

楔形体；波浪；入水；VOF；数值模拟

入水问题广泛存在于船舶、航空、水中兵器及仪器下水等研究领域中，物体在入水时不仅涉及较大的冲击压力，也会产生水体飞溅效应，且入水时间短、流场变化剧烈，实验研究的难度较大，随着数值方法对自由液面追踪及动边界处理的逐渐成熟，数值模拟已成为研究入水过程的重要方法，同时由于研究的深入及对入水压力和姿态要求越来越严格，波浪对入水过程的影响已不可忽略。

数值模拟物体入水的研究较多，如Zhao[1]和Zhu[2]均基于势流理论采用边界元方法研究了楔形体的入水问题，但无法刻画入水过程造成的射流影响；Arai[3]采用带自由表面的两相流模拟方法(VOF)模拟了二维楔、圆柱船艏的砰击入水问题，陈宇翔[4]也采用了VOF方法对圆柱的入水过程进行了模拟，Kleefsman[5]则基于VOF法模拟了二维楔形体的自由落水问题，结果表明：VOF法可以很好地处理自由面重构等强非线性现象；Shao[6]采用了无网格的SPH法计算了物体入水的自由液面及流固相互作用等问题，很好地处理了入水时液面变形较大问题，但数值计算量较大。而波浪中的物体入水研究却较少，其中Faltinsen[7]基于势流边界元理论采用附加质量法，计算了入射波对入水物体的影响，但只能给出物体所受的合力，对于其它细节却无法给出，同时在物体完全入水时，计算结果会受到较大的影响；为此，王文华[8]基于CFD模型并采用自由液面捕捉法模拟了圆柱悬挂入水时波浪的周期性对悬绳受力的影响，但未就楔形体在波浪过程中的入水进行研究；储慧林[9]基于Fluent的VOF法研究了鱼雷入水时波浪对鱼雷受力、空泡闭合等的影响，但其考虑的物体入水为匀速状态，而实际物体在入水初期受到较大的冲击压力，其速度及姿态均会发生较大的改变。

基于计算流体力学模型(Fluent)，采用VOF法，并利用自定义函数，模拟了楔形体的自由入水过程。同时结合推波板原理[10]及海绵层消波理论[11]实现了数值水槽的造消波，在波浪稳定后，控制楔形体的向下运动，实现了波浪中楔形体自由入水的模拟，计算了楔形体入水时所受的水作用力，以及自由面的变化和物体表面的压强分布等，同时研究了不同波高、周期和在波浪不同位置入水对楔形体入水的影响过程，数值结果对研究复杂海况下的物体入水问题具有一定的参考意义。

1 数学模型

1.1基本方程

对于不可压缩流体，在直角坐标系下其运动规律可以用N-S方程来描述，包括连续性和动量方程分别为：

式中：uj为(x,y,z)三个方向上的流速分量；Fi为单位质量力沿(x,y,z)三个方向的分量；P为压强；υt为紊流粘性系数，本文采用k-ε湍流闭合模型对其求解。

自由面追踪采用VOF法，即通过求解单独的动量方程和处理穿过区域的每一流体容积比来模拟两种或多种不能混合的流体。定义体积函数αq代表第q种流体，对任一单元存在三种可能，即：αq=0表示该单元第q流体不存在；αq=1表示该单元充满第q流体；0<αq<1表示该单元存在着流体之间的界面。

以第q流态为例，其体积函数的输移扩散方程：

在任一单元中控制方程的特性参数是由几种流体的组合表示，以q1和q2两种流态为例，那么单元体的密度可以表示为式(4)，其它特性参数如粘性系数等均按此方法计算。

模型中楔形体视为刚体结构，不发生受力变形，根据牛顿第二定律，流体中运动的刚体动力学方程定义为：

(5)

式中：F、M′为物体所受力及力矩，m为物体质量，[IG]为惯性矩，VC表示物体平动速度，w表示物体角速度。

对由固体运动造成的动边界问题则采用动网格技术，即完成每一步物体的运动状态计算后重新划分网格。为详细刻画物体入水时的射流现象，在物体周围设置移动加密网格，该计算域网格随物体一起下移。而物体的运动则使用六自由度模型计算，并通过自定义函数define_sdof_properties(name,prop,dt,time,dtime)来定义其质量及转动惯量等。

数值计算中采用速度和压力场耦合(Coupled)算法，VOF模型采用自由面重构方法来处理液面变化，湍流采用k-ε两方程模型和壁面函数法，压强计算采用体积力加权(Body Force Weighted)二阶差分格式，密度和动量均采用二阶迎风格式。

1.2数值造波与消波方法

本文根据线性造波机原理，将计算域的左边界设置为一个运动边界即造波板，用以模拟活塞式造波机运动，从而生成规则波。在原点设置一冲程为S、圆频率为ω的造波机做简谐运动，得到其水平位移和速度分别为：

得到在水深为d的波浪水槽中，产生的波面方程为：

式中：k为ω2=gktanh(kd)的正实根；kn为方程ω2=-gktanh(kd)的正实根，式右边第二项为造波机产生的衰减立波，其随着离造波板距离的增加而以指数型式衰减，可以忽略。剩下的第一项即为造波机产生的行进波，其波高为2S[cosh(2kd)-1]/[2kd+sinh(2kd)]，圆频率即为ω。造波板运动由自定义函数define_cg_motion(name,dt,vel,omega,time,dtime)来定义。

为降低初始扰动，在初始2个波周期(T=2π/ω)内对造波板的运动进行平滑，具体如下：

为消除水槽前后端对波浪的反射作用，引入动量源消波法，在动量方程的右端增加一个动量衰减的源项[12]，即在水槽末端添加至少一倍于波长的消波段：

式中：μ为消波系数，沿波浪传播方向取线性分布，-μui为消波项，在Fluent模型中由自定义函数define_source(name,c,t,dS,equ)进行添加，消波后水槽右端边界为固壁形式。

2 数值试验及结果分析

2.1楔形体在静水中的入水过程

Zhao[13]曾完成了楔形体在静水中自由入水过程的研究。依此，本文刚性楔形体的参数选择如下：斜升角为30°，宽度为0.5 m，高度为0.29 m，质量为241 kg，长度为1.0 m，在数值计算中，初始时刻为楔形体顶点接触平静自由液面的瞬间，楔形体初始速度为-6.15 m/s，随后开始自由入水。由于冲击问题对网格要求较高，不同密度网格对计算结果的影响可能较大，因而在模拟锲形体入水时首先要进行网格无关性验证。设计四种不同尺度网格，分别为工况1：最小网格尺寸(楔形体处)为0.02 m，最大网格尺寸(边界处)为0.1 m，整体网格单元数为18 653个，网格节点数为9 480个；工况2：最小和最大网格尺寸为0.01和0.07 m，单元数为40 692个，节点数为20 587个；工况3：最小和最大网格尺寸为0.01和0.05 m，单元数为74 630个，节点数为37 624个，其局部网格如图1所示；工况4：最小和最大网格尺寸为0.005和0.03 m，单元数为268 526个，节点数为134 800个。数值计算时间步长均为0.000 1 s，利用上述四种工况计算得到楔形体入水后的垂向水动力变化对，比如图2所示。从图2可以看出随着网格密度的增大垂向水动力的波动越小变化越稳定，在工况3中数值结果已较为平稳，为保证计算结果的准确性，同时减少计算量，后续入水计算选用工况3中的网格分辨率。

为分析数值模拟过程中的收敛性，图3给出了上述工况1和工况3在初始计算时的残差变化，其中残差的定性收敛值为10-4，每一步的最大迭代步数为200步，由于数值计算为非稳态，因此在每一步更新时残差均会变大，从图3可以看出除第一步外其余每步的迭代计算残差会很快降到10-4以下，且能量残差(k)均在10-6以下，说明数值计算的每一步迭代均能很快达到收敛。

基于工况3数值计算得到楔形体的垂向水动力和垂向速度，与实验结果及Kleefsman的数值结果进行对比，如图4(a)和4(b)所示，图中F代表楔形体受到水体的垂向水动力，V代表楔形体的垂向速度，横坐标为时间。从图4可知，本文数值模式很好了模拟了楔形体在入水过程中的受力及速度变化，楔形体所受的最大垂向水动力主要发生在入水初期的抨击阶段。

图1 楔形体在静水中自由入水的网格划分Fig.1 Numerical grid for the free water-entry wedge

图2 不同网格数下楔形体入水后的垂向水动力变化Fig.2 Comparison of vertical hydrodynamic force for water-entry wedge between differernt meshes

图3 工况1和3中楔形体入水后的残差变化Fig.3 The residual variation of the free water-entry wedge in case 1 and 3

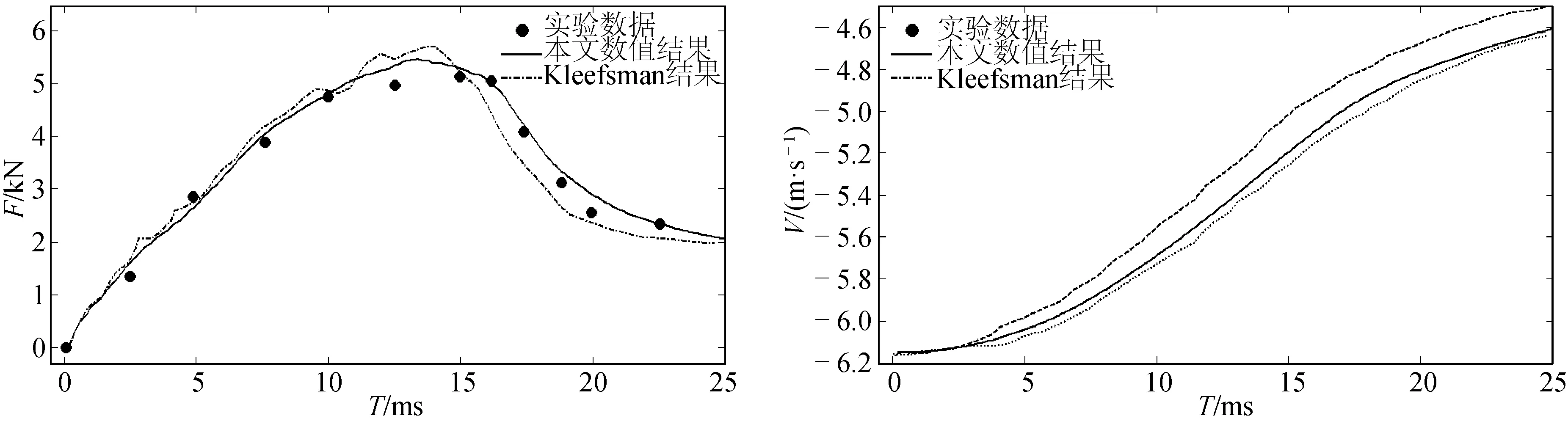
图4 楔形体垂向水动力和速度与实验数据和Kleefsman结果对比Fig.4 Comparison of vertical hydrodynamic force and velocity between simulation and experiment

同时得到入水初期不同时刻的速度矢量及自由液面变化，如图5所示。从图5可知，楔形体入水后会对水体产生挤压，会使得水体沿斜边产生射流，同时在楔形体底部斜边和自由液面之间的空气会受到挤压而向两侧逃逸，并在斜边末端发生分离，从而形成一组对称的空气漩涡。

为描述楔形体从入水到浸没的过程，以及楔形体两侧射流变化形态，图6给出了从t=0 s到t=0.8 s中每隔0.1 s水体自由液面变化过程。数值结果详细描述了从楔形体接触水面到空泡形成再到空泡闭合的整个过程；而楔形体入水造成的两侧射流基本对称，且在重力的作用下，射流逐渐弯曲向下，并最终融入两侧水体中。

图5 不同时刻自由液面形状和速度矢量Fig.5 Free surface profile and velocity vectors for free falling wedge at various water entry moments

图6 楔形体从入水到浸没过程中自由液面变化Fig.6 Free surface profiles of the free falling wedge from water-entry and water-immersion

2.2波浪数值水槽的构建

为分析数值波浪水槽的造波功能，完成楔形体在波浪中入水的数值模拟，建立如图7所示的200.0 m×12.0 m的数值水槽。为减少数值计算量，在楔形体入水区域采用三角形加密网格，而在其它波浪传播区域则采用矩形网格，最小网格尺寸(楔形体附近)0.01 m，垂向最大网格尺寸0.05 m，水平向最大网格尺寸0.5 m，整体网格单元数(包括矩形和三角形)324 472个，网格节点数208 281个。水槽自左向右分别为前端缓冲区、波浪传播区和后端消波区域，而楔形体的入水区则放在波浪传播区域，造波板设置在水槽的左边界上，且为坐标原点。

图7 波浪数值水槽示意Fig.7 Sketch of Cartesian cut cell mesh and zone partition in numerical wave flume

为验证数值水槽造消波的有效性，首先模拟波高Hs=1.0 m、周期T=4.0 s的二维规则波，不考虑楔形体的入水过程。根据线性造波机理论，得出造波板的往复运动为S=0.583 6 m、ω=1.57 s-1。

计算得到x=50、100及150 m处的波高过程线如图8所示。从图8可知在x=50、100及150 m处波高分别约为0.98、0.95和0.9 m，波浪在传播过程中受粘性的影响会发生一定的衰减。图9给出了计算区内的波面过程线和波浪内部的流场分布。从图9可知波面过程线及波浪内的流场分布均符合线性波理论。

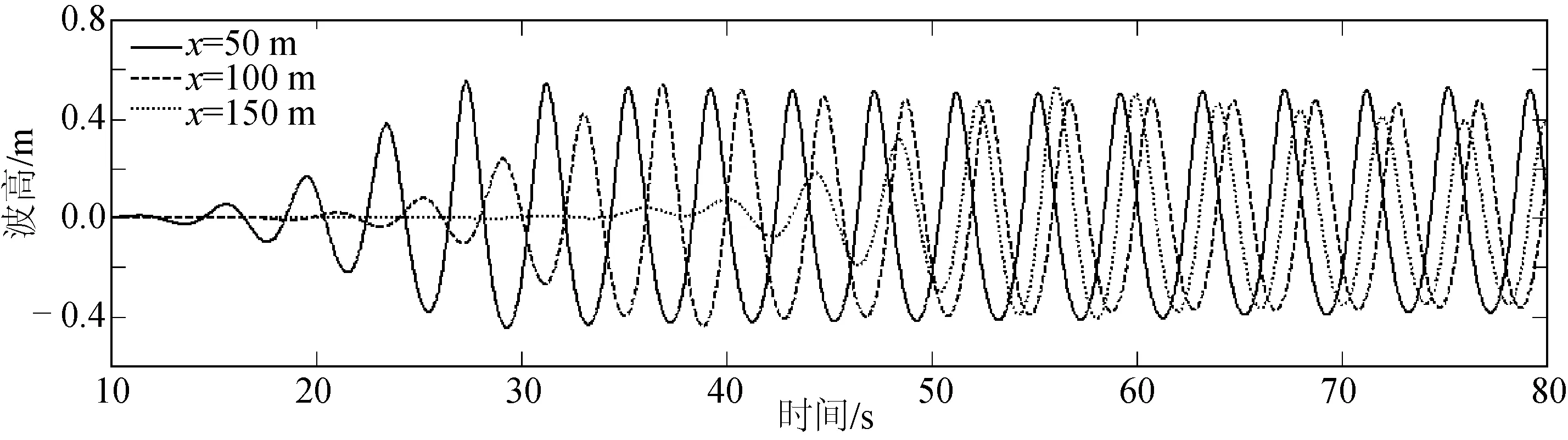
图8 不同位置处的波面时间过程线Fig.8 Time series of wave profile at x=50 m,x=100 m,x=150 m and x=190 m

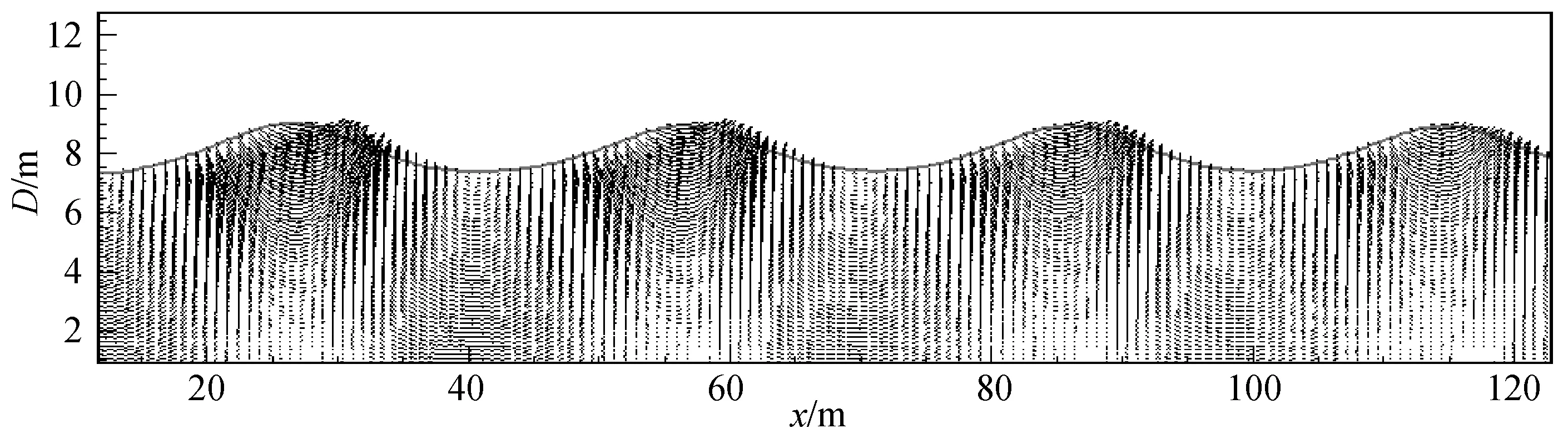
图9 数值水槽内波浪波形及流场分布Fig.9 Free surface and velocity field in numerical flume

2.3楔形体在波浪中入水的计算

波浪数值水槽分别模拟不同波高和周期的波浪，同时设置楔形体的入水时间和入水速度，使得楔形体在波浪的波峰、平衡位置(速度向下)、平衡位置(速度向上)、波谷处入水，且入水时的速度均为-6.15 m/s，楔形体在波浪不同位置处入水示意如图10所示。

图10 楔形体在波浪不同位置处入水示意Fig.10 Sketch of the free falling water-entry wedge in the wave

数值计算得到周期为4 s、波高不同时楔形体的垂向水动力及速度变化对比，如图11所示，以及波高为1 m、周期不同时楔形体在波峰处入水后的垂向水动力及速度变化对比，如图12所示。

从上述结果可以看出，楔形体在波峰处入水，随着波高的增加，入水初期的垂向水作用力峰值会减小，而速度变化变缓，结论和文献[14]相同；随着周期的增大，入水初期的垂向水动力峰值略有增大，并趋近于无波浪的入水过程。

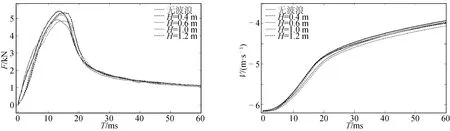
图11 不同波高下楔形体在波峰入水时的垂向水动力及速度变化对比Fig.11 Comparison of vertical hydrodynamic force and velocity under different wave heights

图12 不同周期下楔形体在波峰入水时的垂向水动力及速度变化对比Fig.12 Comparison of vertical hydrodynamic force and velocity under different wave periods

同时模拟研究了楔形体在波浪Hs=1.0 m、T=1 s的波谷、平衡位置(速度向下)和平衡位置(速度向上)三种情况下入水的垂向水作用力及垂向速度变化，如图13所示。

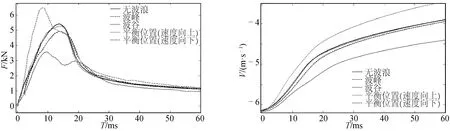
图13 楔形体在波浪不同位置处入水的垂向水动力及速度变化对比Fig.13 Comparison of vertical hydrodynamic force and velocity under different positions

从图13可知：楔形体在波浪平衡位置(速度向上)处入水时所受的垂向水动力峰值最大，大于无波浪情况，造成垂向速度的降低更为显著；而在平衡位置(速度向下)处入水时初期所受的垂向水动力最小，小于无波浪情况，其速度变化更缓，且在上述两个位置处入水时受力均出现了类似双峰值情况；在波峰和波谷处入水受力峰值均小于无波浪情况，但较平衡位置其对峰值和垂向速度的改变均不显著。

由于楔形体入水后的压力变化主要发生在入水初期，其上述差异主要受波形及行进波内速度场影响，根据图9中波浪内速度场可以看出：当波浪内流速垂直向上时，楔形体入水时所受的作用力会变大，反之则会减小；而平衡位置入水时受波形影响，楔形体两个斜边的入水抨击时间会不同，进而造成楔形体受力出现双峰值情况；而随着波高的增大及周期的减小，行进波内的流速会逐渐增大，从而对楔形体入水的影响也越来越明显，反之则逐渐趋近于静水状态下的入水过程；在波峰及波谷处由于垂向速度较小，其造成的楔形体的受力及垂向速度改变较平衡位置不明显。

图14(a)和图14(b)分别给出了楔形体在波峰及平衡位置(速度向上)处入水时，从T=0 s到T=0.8 s中每隔0.1 s时水体自由液面变化过程，以及每隔0.2 s时的楔形体位置示意。同静水中楔形体入水造成的自由液面变化(图4)对比可知，由于波浪的作用，楔形体入水造成的射流不再呈对称形状；波浪会对楔形体入水后的姿态产生影响，且在波浪不同位置处入水影响也有所差异。

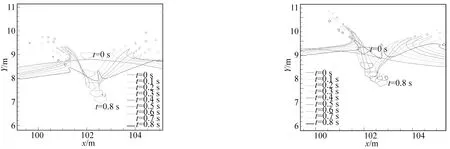
图14 楔形体在波峰及平衡位置(速度向上)处入水时的自由液面变化Fig.14 Free surface profiles of the wedge wave-entry at wave crest and equilibrium positions

图15和图16分别给出楔形体在静水及波浪的波峰、波谷、平衡位置(速度向下)和平衡位置(速度向上)中入水时斜边压强分布历程。由图可知：在静水中楔形体斜边上两侧的压强始终为对称分布，而在波浪中入水时初期斜边压强均为不对称分布。在波峰处主要受波浪内水平流速的影响造成斜边压强的左大右小；在平衡位置(速度向下)时斜边压强也为左大右小，主要由于在0.02 s时，受波形的影响楔形体右侧斜边已发生入水抨击(图11)，而左侧斜边仍处于水体的砰击作用中；在平衡位置(速度向上)时压强为左小右大，也是由于波形造成斜边浸入水体时间不同造成，而在楔形体完全浸入水中后(0.1 s后)两斜边压力均基本一致。

图15 楔形体在静水及波浪波峰处入水时斜边压强分布历程Fig.15 Hypotenuse pressure distribution of the wedge wave-entry at still wave and wave crest

图16 楔形体在波浪平衡位置(速度向下、速度向上)处入水时斜边压强分布历程Fig.16 Hypotenuse pressure distribution of the wedge wave-entry at different equilibrium positions

3 结 语

基于计算流体力学模型(Fluent)，采用VOF法并利用动网格技术及自定义函数验证了楔形体的自由入水过程，同时利用数值造消波方法模拟了楔形体在波浪中的入水过程，研究了波浪对楔形体入水初期的冲击压力、速度变化的影响，以及在波浪中不同位置入水时对入水压力、斜边压强分布以及入水姿态变化的影响。

本文建立的入水模型可较好地模拟楔形体入水造成的射流及空泡的形成发展过程，而波浪对楔形体入水的影响主要由波浪内部流场变化及表面波形决定，结论符合之前的研究成果，数值方法及结论对复杂海况下的海洋构件入水具有一定的参考意义，由于计算量的限制，本文并未考虑三维实际情况，后续研究应予以关注。

[1] ZHAO R,FALTINSEN O M.Water-entry of two-dimensional bodies [J].Journal of Fluid Mechanics,1993,246: 593-612.

[2] ZHU X Y,FALTINSEN O M,HU C H.Water entry and exit of a horizontal circular cylinder [J].Journal of Offshore Mechanics and Arctic Engineering,2007,129:253-264.

[3] ARAI M,CHEN L Y,INOUE Y.A computing method for the analysis of water impact of arbitrary shaped bodies [J].Journal of Computational Physics,1981,39:201-225.

[4] 陈宇翔，郜冶，刘乾坤.应用VOF方法的水平圆柱入水数值模拟[J].哈尔滨工程大学学报,2011,11(32): 1 439-1 442.(CHEN Y X,GAO Y,LIU Q K.Numerical simulation of water-entry in a horizontal circular cylinder using the volume of fluid (VOF) method [J].Journal of Harbin Engineering University,2011,32(11): 1 439-1 442.(in Chinese))

[5] KLEEFSMAN K M T,FEKKEN G,VELDMAN A E P,et al.A volume of fluid based simulation method for wave impact problems [J].Journal of Computational Physics,2005,206: 363-393.

[6] SHAO S D.Incompressible SPH simulation of water entry of a free-falling object [J].Int.J.Numer.Meth.Fluids,2009,59: 91-115.

[7] FALTINSEN O M.Sea loads on ships and offshore structures [M].UK: Cambridge University Press,1990.

[8] 王文华,王言英.圆柱在波浪中入水的数值模拟[J].上海交通大学学报,2010,10(40): 1 393-1 399.(WANG W H,WANG Y Y.Numerical study on cylinder entering water in wave [J].Journal of Shanghai Jiaotong University,2010,44(10): 1 393-1 399.(in Chinese))

[9] 储慧林.鱼雷在波浪中入水的数值模拟[D].镇江: 江苏科技大学,2014.(CHU H L.Numerical simulation of torpedo entering water in wave [D].Zhenjiang: Jiangsu University of Science and Technology,2014.(in Chinese))

[10] LARSEN J,DANCY H.Open boundaries in short wave simulations—a new approach [J].Coastal Engimeering,1983,7(3): 285-297.

[11] 陶建华.水波的数值模拟[M].天津: 天津大学出版社,2005.(TAO J H.Numerical simulation of water waves [M].Tianjin: Tianjin University Press,2005.(in Chinese))

[12] 王鹏,孙大鹏,吴浩.海堤上波浪爬高和越浪分析[J].海洋工程,2011,29(4):97-107.(WANG Peng,SUN Dapeng,WU Hao.Numerical simulation of wave runup and overtopping over seawalls [J].The Ocean Engineering,2011,29(4):19-107.(in Chinese))

[13] ZHAO R,FALTINSEN O M,AARSNES J.Water entry of arbitrary with and without flow separation[C]//Proceedings of the 2-d Sections 21st Symposium on Naval Hydrodynamics.1997.

[14] 王文华.物体入水问题的分析研究及其在船舶与海洋工程中的应用[D].大连: 大连理工大学,2010.(WANG W H.Analysis and research on water entry problem and its application in ship and ocean engineering [D].Dalian: Dalian University of Technology,2010.(in Chinese))

Numerical study of the free water-entry wedge in wave

WANG Ping1,YUAN Shuai1,ZHANG Ningchuan2,CHEN Weibin1,CHEN Yuan1

(1.National Marine Environmental Monitoring Center,Dalian 116023,China; 2.Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)

Wave impact in body water-entry cannot be ignored.Based on the hydrodynamic model,the free falling wedge water-entry cases are simulated by using the volume of fluid (VOF) method and user-defined functions.Considering the push-wave plate principle with sponge layer theory,the numerical wave flume was built.The free falling wedge in wave water-entry case was simulated,and the vertical hydrodynamic force,velocity and pressure distributions of the wedge were computed.The influence of different wave heights,wave periods and positions on wedge water-entry was also studied.Numerical results show that the free surface profile and bubble development of wedge water-entry can be simulated accurately by the module.The influence of wave on wedge water-entry was decided by the free surface and velocity field in wave flume,and the water-entry positions in wave flume had a greater impact on the wedge force and form after entering the water.

wedge; wave; water-entry; the volume of fluid (VOF) method; numerical simulation

P751

A

10.16483/j.issn.1005-9865.2017.05.005

1005-9865(2017)05-0042-09

2016-09-22

国家自然科学基金(51709054)；海洋公益性行业科研专项资助项目(201405025；201505019)

王 平(1988-)，男，安徽人，助理研究员，从事近岸动力学研究。