基于遗传BP神经网络的超临界水自然循环稳态流量研究

齐 实，周 涛，周蓝宇，黄彦平

(1.华北电力大学核科学与工程学院，北京 102206；2. 华北电力大学核热工安全与标准化研究所，北京 102206；3.南华大学核科学技术学院，湖南 衡阳 421001；4.中核核反应堆热工水力技术重点实验室，四川 成都 610041)

基于遗传BP神经网络的超临界水自然循环稳态流量研究

齐 实1，2，周 涛1，2，周蓝宇3，黄彦平4

(1.华北电力大学核科学与工程学院，北京 102206；2. 华北电力大学核热工安全与标准化研究所，北京 102206；3.南华大学核科学技术学院，湖南 衡阳 421001；4.中核核反应堆热工水力技术重点实验室，四川 成都 610041)

利用遗传BP神经网络建立超临界水自然循环稳态流量预测模型，采用平均影响值(MIV)的概念进行参数敏感度分析。研究结果表明，遗传 BP网络可以很好的预测超临界水自然循环稳态流量值，误差落在了±10%范围内。在所选的参数范围内，入口温度增大，稳态流量减小，提高试验段高度或减小加热段长度、出入口阻力系数可以使自然循环流量增加，其重要度排序为入口温度、试验段高度、入口阻力系数、出口阻力系数、加热段长度，且入口阻力系数、出口阻力系数、加热段长度影响基本对等。

超临界水；自然循环；稳态流量；遗传BP神经网络

超临界水冷堆[1-2](SCWR)作为第四代反应堆中唯一的水冷堆，堆芯工作压力25MPa，出口冷却剂温度500℃左右，具有经济性、系统简单和可持续性等诸多综合优势。由于超临界水在临界点附近物性会发生剧烈变化，因此超临界水冷堆可能出现流动不稳定性。

国内外一些学者[3-4]通过数值模拟或实验进行了超临界水强迫循环下流动稳定性的研究。自然循环条件下，超临界水流动稳定性作为新兴的研究内容，一些研究者在理论和实验方面进行了部分研究。俞冀阳等人[5]采用清华大学的超临界水自然循环实验台架验证其数值模拟结果，认为实验回路中处于功率流量的负斜率区内，没有Ledinegg不稳定性发生。Debrah等人[6]利用Relap5程序分析中国原子能研究院超临界自然循环实验台架，采用无量纲分析方法进行超临界水自然循环流动不稳定性的研究。然而，影响超临界水稳定性的因素具有耦合特点，且在不同的实验参数范围内同一种因素具有多种不同的机制，难以分析各因素与流动稳定性边界的关系。

目前，关于不同参数的影响多采用单一因素分析，即对某一系统参数进行微小变动，同时固定其他参数值，进行分析计算。但是由于耦合关系的存在，单因素分析方法可能存在误差。遗传BP神经网络(GNN)结合了遗传算法和BP神经网络的优点，具有全局搜索的优势，是一种新的处理非线性关系的数学工具[7]，可以较好分析各因素对稳定性边界的影响。研究将GNN网络用于预测超临界水自然循环稳态流量及各影响参数敏感度分析，为进一步研究奠定基础。

1 遗传神经网络方法

1.1 BP神经网络

BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈网络。由于BP网络具有结构简单、可调整的参数多、能够学习和存储大量的输入—输出模式映射关系，无需事前知道这种映射方式的数学方程等特点，BP网络获得广泛应用。

Robert Hecht证明了对任何在闭区间内的连续函数，都可以用一个隐层的BP网络来逼近，一个三层的BP网络可以完成任意的n维到m维的映射。因此，采用三层神经网络进行分析。其结构如下[8-9]。

Y=Purelin[Lw2×
Tansig(Iw1×Pn+B1)+B2]

(1)

式中，Y为BP网络的输出量；Pn为BP网络的输入向量；Iw1、Lw2分别为输入层到隐层、隐层到输出层的网络连接权值；B1、B2分别为输入层到隐层、隐层到输出层网络连接阈值；Tansig为输入层到隐层之间的传递函数；Purelin为隐层到输出层之间的传递函数。

Dombi等人提出平均影响值(MIV，Mean Impact Value)的概念。MIV[10]应用神经网络中权重矩阵的变化情况来评价各个自变量对因变量影响，同时MIV也被认为是神经网络中评价输入神经元对输出神经元影响大小的最好的指标之一。MIV符号代表相关的方向，绝对值大小代表影响的相对重要性。具体步骤为在BP网络训练和测试结束后，将原训练样本中每一个自变量在其原值的基础上分别加/减10%构成新的两个样本，将新的样本利用已经建成的网络进行仿真，得到两个仿真结果，求出相应的差值即为变动产生后对输出产生的影响变化值(IV，Impact Value)，最后将IV平均得到自变量对因变量输出MIV。重复以上步骤，依次计算出各自变量的MIV值，最后根据MIV绝对值的大小为各自变量排序，得到各自变量对因变量影响重要程度次序。

1.2 遗传算法

遗传算法[11](Genetic Algorithm)是模拟自然界遗传机制和生物进化论而成的随机搜索算法。它把自然界“优胜劣汰，适者生存”的进化原理引入优化参数形成的串联编码群体中，按照选择的适应度函数对个体进行筛选，使适应度好的个体被保留。这样，反复循环，新的群体既继承上一代信息，又优于上一代。其基本操作如下：

(1) 选择操作

选择操作是指从旧群体中选择适应度值好的个体到新的群体中。

(2) 交叉操作

交叉操作是指从群体中选择两个个体，通过染色体交换组合，产生新的优秀个体。

(3) 变异操作

变异操作是指从群体中任选一个个体，选择染色体中的一点进行变异以产生更优秀的个体。

1.3 优化BP网络方法

虽然BP神经网络在核反应堆热工水力方面已经得到广泛应用[12-13]，但是BP神经网络存在一些缺陷，如学习收敛速度太慢、容易陷入局部极小点[10]。有限的超临界水自然循环稳态流量数据凸显了BP网络缺陷。针对以上存在的问题，综合遗传算法(GA)与BP神经网络的优点，利用遗传算法优化神经网络的阈值和权重，可以提高神经网络的精度，进而可以更好的采用MIV方法进行变量的筛选。图1为利用遗传神经网络(GNN)进行预测超临界水自然循环稳态流量及其影响因素敏感度分析流程图。

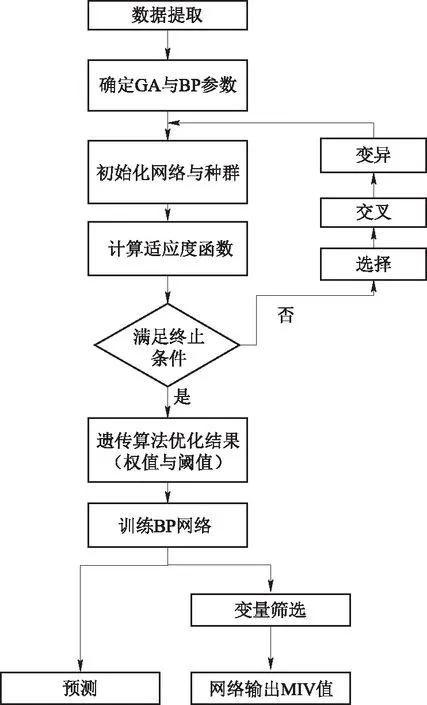
图1 遗传BP神经网络流程Fig.1 Flow Chart of Genetic Neural Network

从图1可知，采用遗传算法对BP神经网络的权值和阈值进行优化，将其优化的值传递给BP神经网络进行训练，使其能够得到更精确的网络。将超临界水自然循环稳态流量作为函数输出值，将影响稳态流量的系统参数、热工参数作为输入值，通过反复训练，得到稳定的网络，用于预测稳态流量及筛选其影响因素。

2 参数选择及模型计算

2.1 参数选择

Chatoorgoon在自然循环回路内进行超临界水流动的相关研究中发现，稳态情况下，超临界水的自然循环流量随着加热功率的增加而增加，当流量达到一个最大值后，流量随着功率的继续增加而减小，稳态情况下，最大流量对应的加热功率是超临界水稳定边界的类似，即为稳态流量。选定Chatoorgoon等人[14-15]93组数据，影响稳态流量的因素主要包括：加热段长度、入口温度、试验段高度、入口和出口阻力系数。参数范围如表1所示。

表1 参数范围Table 1 Parameter Ranges

2.2 神经网络建立及验证

采用GNN网络进行稳态流量预测。选取表1中参数加热段长度、入口温度、实验段高度、入口和出口阻力系数作为输入参数，稳态流量作为输出参数。取种群为50，交叉概率为0.3，变异概率为0.05。采用单隐层的3层网络，隐层节点数q采用经验公式确定。

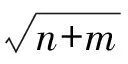
(2)

式中，n、m分别为输入层、输出层神经元数，r为1～10间的任意整数。本文中，输入层数为5，输出层数为1，r值取5，采用公式(2)算得隐层节点数为7。随机选取训练数据78组，15组进行测试，GNN神经网络预测的稳态流量与实际值对比结果如图2所示。

图2 GNN预测结果与实际结果对比Fig.2 Comparison between GNN Prediction and Actual Results

从图2可知，GNN网络对超临界水自然循环稳态流量的预测结果与实际结果吻合良好，误差落在±10%范围内。另外由于神经网络具有随机性，引入平均绝对相对误差MAD、标准偏差SD来评价GNN神经网络。

(3)

(4)

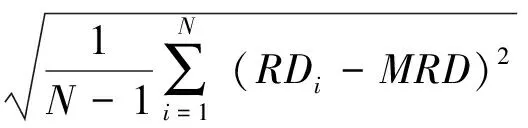
(5)

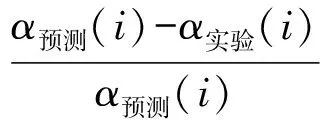
(6)

其中，平均绝对相对误差表示预测值与实际值之间差距的大小。标准偏差表示的是神经网络预测数据偏离算数平均值的程度大小，标准偏差越小，表示这些数值偏离平均值就越少，反之则偏离平均值的程度越大。GNN网络的平均绝对相对误差MAD、标准偏差SD分布如表2所示。

表2 GNN模型预测误差分析Table 2 Prediction error of GNN model

2.3 单因素对稳态流量的影响

利用GNN神经网络预测单因素对稳态流量的影响与表1范围内的实际值对比如图3所示。

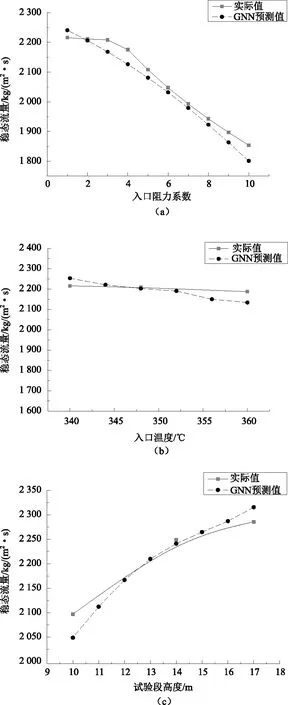
图3 单因素对稳态流量的影响Fig.3 Influence of single factor on steady-state mass flow(a) 入口阻力系数对稳态流量的影响；(b) 入口温度对稳态流量的影响；(c) 试验段高度对稳态流量的影响

图3(a)所示的是加热段长度为1m，入口温度340℃，实验段高度14m，出口阻力系数为1的条件下，入口阻力系数对稳态流量的影响。可以看出，随着入口阻力系数的增大，稳态流量值逐渐减小。这是因为入口阻力系数增加，自然循环系统的阻力压降损失增大，自然循环能力减弱，从而稳态流量减少。图3(b)所示的是试验段高度为14m，加热段长度为1m，入口阻力系数与出口阻力系数均为1条件下，入口温度对稳态流量的影响。可以看出，随着入口温度增大，稳态流量逐渐减小。这是因为入口温度升高，达到稳态流量需要的热量越少，因此，自然循环系统冷热段密度差减小，稳态流量减小。图3(c)所示的是入口温度为350℃，加热段长度为2m，入口和出口阻力系数均为1条件下，试验段高度对稳态流量的影响。可以看出，随着试验段高度增加，稳态流量逐渐增加。这是因为试验段高度增加，冷热段流体密度差增加，因此，自然循环驱动力增加，导致稳态流量增加。从以上图中可知，GNN网络预测误差较小。

2.4 入口温度与入口阻力系数综合效应对稳态流量的影响

在表1数据中，取加热长度为2m，试验段高度为14m的实验数据，其中入口温度350～360℃，同时入口阻力系数1～10，共20组数据，输入训练好的GNN神经网络，得到入口温度与入口阻力系数综合效应对自然循环稳态流量影响如图4所示。

图4 预测结果和实际结果Fig.4 Prediction results and actual results(a) GNN神经网络预测结果；(b) 实际结果；(c) 误差分析

2.5 不同影响因素敏感性分析

按照表1中的参数范围，采用MIV方法，用训练好的GNN神经网络进行参数敏感度分析。结果如表3所示。

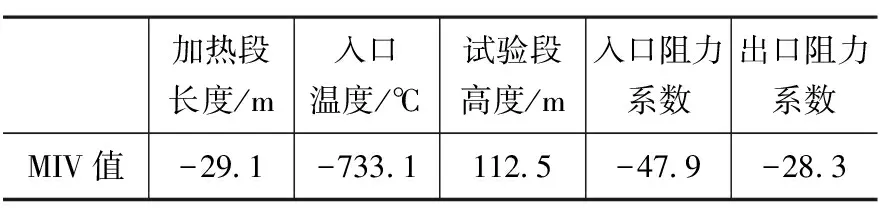
表3 各影响因素MIV值Table 3 MIV of each factor

从表3中可知，在Chatoorgoon等人研究的参数范围内，稳态流量受入口温度的影响最大，且其影响效应负相关。即入口温度越大，稳态流量越小。这是因为当入口温度过高时，达到稳态边界最大流量时加热功率较低，因此冷热段密度差较小，从而驱动压头较小，稳态流量较低。另一方面，超临界水在拟临界点附近密度和比热随着温度发生剧烈变化，入口温度接近拟临界点附近，当入口温度发生较小变化时，相应的密度和比热发生较大的变化，从而对稳态流量影响较大。其次为试验段高度，影响效应正相关。这是因为随着试验段高度的增加，冷热流体的密度差增大，从而驱动压头增大，稳态流量值增加。自然循环的主要驱动力为冷热流体的密度差，增大试验段高度，可以增加驱动力，从而对稳态流量有着较大的影响。入口阻力系数的影响为负相关，这是因为入口阻力系数增加，自然循环系统的阻力压降损失增大，自然循环能力减弱，从而稳态流量减少。出口阻力系数的影响与进口阻力系数类似。最后，对自然循环影响最小的为加热段长度，在参数范围内，其总体影响为负相关。这是因为一方面，自然循环加热段长度增加，可以加长流体的受热区域，另一方面，由于加热段长度增加，自然循环稳定功率减少。当以上两个方面综合作用使系统内密度差增大，系统稳态流量增加，反之，减小。都立国等[16]研究得到的参数重要度顺序与表3所得到的参数重要度分析一定程度上吻合。进一步说明了神经网络算法可以对影响超临界水稳态流量的参数进行重要度筛选。

3 结论

利用GNN神经网络算法对超临界水自然循环稳态流量进行分析，得到了不同参数对稳态自然循环流量的影响，具体结论如下。

(1) GNN神经网络可以很好的预测超临界水自然循环稳态流量值，其预测值与实际值预测误差落在了±10%范围内。

(2) 采用GNN网络可以很好的预测单因素和综合效应对自然循环稳态流量的影响。随着入口阻力系数增加，自然循环系统的阻力压降损失增大，自然循环能力减弱，从而稳态流量减少。入口温度和入口阻力系数对稳态流量的影响不是单调函数的关系。GNN网络预测结果与实际数值符合良好。

(3) 对于自然循环稳态流量，提高试验段高度或减小加热段长度、入口温度、出入口阻力系数可以使自然循环流量增加，其重要度排序为入口温度、试验段高度、入口阻力系数、出口阻力系数、加热段长度，且入口阻力系数、出口阻力系数、加热段长度影响基本对等。

[1] 程旭，刘晓晶.超临界水冷堆国内外研发现状与趋势[J]. 原子能科学技术，2008，42(2)：167-172.

[2] Oka，Y.，Koshizuka，S.，Ishiwatari，Y.，2010. Super Light water reactors and super-fast reactors：Supercr-itical-pressure light water cooled reactors[M]. New York：Springer. 2010.

[3] LI Jingjing，ZHOU Tao，SONG Mingqiang，et al. CFD analysis of supercritical water flow instability in parallel channels[J]. International journal of heat and mass transfer，2015，86：923-929.

[4] ZHANG Lei，CAI Benan，WENG Yu，et al. Exper-imental investigations on flow characteristics of two parallel channels in a forced circulation loop with supercritical water[J]. Applied Thermal Engineering，2016，106：98-108.

[5] Yu J.Y.，Che S.W.，Li R.，Qi B.X..Analysis of Ledinegg flow instability in natural circulation at supercritical pressure[J]. Progress in Nuclear Energy，2011，53：775-779.

[6] Debrah Seth Kofi，Ambrosini Walter，Chen Yuzhou. Discussion on the stability of natural circulation loops with supercritical pressure fluids[J]. Annals of Nuclear Energy，2013，54：47-57.

[7] 罗毅，刘峰.基于遗传神经网络的风电场输出功率短期预测[J]. 华东电力，2012，40(7)：1205-1208.

[8] 李满峰，李素萍，范波. 基于遗传神经网络的太阳能集热器仿真研究[J]. 中国电机工程学报，2012，32(5)：126-130.

[9] 李精精，周涛，段军等. 基于遗传神经网络方法的流动不稳定性起始点研究[J]. 核动力工程，2014，35(2)：63-66.

[10] 王小川，史峰，郁磊. Matlab神经网络43个案例分析[M]. 北京航空航天大学出版社，2013.

[11] 周明，孙树栋.遗传算法原理及应用[M]. 北京：国防工业出版社，2001.

[12] 黄彦平，单建强，陈炳德等. 人工神经网络在圆管临界热流密度数据分析中的应用研究[J]. 核科学与工程，2003，23(1)：45-51.

[13] Su Guanghui，K. Morita，K. Fukuda，et al. Analysis of the critical heat flux in round vertical tubes under low pressure and flow oscillation conditions. Applications of artificial neural network [J]. Nuclear Engineering and Design，2003，220：17-35.

[14] V.Chatoorgoon， A.Voodi，D.Fraser. The stability boundary for supercritical flow in natural convection loops Part I：H2O studies[J]. Nuclear Engineering and Design，2005，235：2570-2580.

[15] V.Chatoorgoon. Stability of supercritical fluid flow in a single-channel natural-convection loop[J]. International Journal of Heat and Mass Transfer，2001，44：1963-1972.

[16] 都立国，匡波，顾汉洋，等. 超临界压力水循环系统非线性水动力特性研究[J]. 核动力工程，2009，30(2)：21-26.

StudyonSupercriticalWaterSteady-stateMassFlowunderNaturalCirculationBasedonGeneticNeuralNetwork

QIShi1，2，ZHOUTao1，2，ZHOULan-yu3，HUANGYan-ping4

(1.School of Nuclear science and Engineering，North China Electric Power University，Beijing 102206，China；2.Nuclear safety and Thermal power Standardization Institute，North China Electric Power University，Beijing 102206，China；3.College of nuclear science and technology，University of South China，Hengyang of Hunan Prov. 421001，China；4.CNNC Key Laboratory on Nuclear Reactor Thermal Hydraulics Technology，Chengdu of Sichuan Prov.610041，China)

The genetic neural network is established to predict supercritical water steady-state mass flow under natural circulation and the method of mean impact value is used to analyze the sensitivity of parameters. The results show that the predictive values of GNN agree well with the actual values. The errors fall in the limits of ±10%. Within the parameter range，the steady-state mass flow decreases rapidly with inlet temperature increase. The steady-state mass flow increases with test section height increase or heating zone length，inlet and outlet resistance coefficient decrease. The magnitude sequence of above factors is confirmed as inlet temperature，test section height，inlet resistance coefficient，outlet resistance coefficient and heating zone length. The influence is basic equivalence among inlet resistance coefficient，outlet resistance coefficient and heating zone length.

Supercritical water；Natural circulation；Steady-state mass flow；Genetic neural network

2017-03-02

超临界水自然循环流动换热特性研究(2013B40)

齐 实(1994—)，男，吉林长春人，硕士,现从事反应堆热工水力及安全分析

周 涛：zhoutao@ncepu.edu.cn

TL339

A

0258-0918(2017)05-0845-07