改进灰色模型在海上交通综合安全指数预测应用

陈昌源， 戴 冉， 冯纪军， 岳兴旺， 张 杰

(大连海事大学 航海学院， 辽宁 大连 116026)

改进灰色模型在海上交通综合安全指数预测应用

陈昌源， 戴 冉， 冯纪军， 岳兴旺， 张 杰

(大连海事大学 航海学院， 辽宁 大连 116026)

为提高海上交通综合安全指数的预测精度，弥补传统预测方法的不足，构造一种改进的灰色预测模型。在对传统的灰色预测模型GM(1,1)的基本原理和预测精度进行阐述的基础上，引入弱化算子序列对灰色预测模型进行改进，设计一种改进的灰色预测模型。以2004—2013年海上交通综合安全指数4项指标历史数据为基础，进行传统灰色模型预测和改进灰色模型预测，并绘制出2种预测模型的实际值和预测值的拟合曲线。结果表明：改进灰色模型的预测精度和拟合曲线都比传统灰色模型要好，能真实反映海上交通综合安全指数的发展趋势，预测结果具有一定的可靠性和实用性。

海上交通综合指数；改进灰色模型；弱化算子；预测；精度

Abstract: Addressing the inadequacy of traditional prediction methods, an improved grey prediction model is developed for better prediction precision of maritime traffic safety index. After looking at the basic principle and the prediction precision of the traditional grey prediction model, a weakening operator sequence is introduced into the grey prediction model GM (1, 1) to improve it. The traditional grey model and the improved gray model are respectively used to process the historical data during the period of from 2004 to 2013 and make predictions of the maritime traffic safety indexes. The predictions are compared with the actual values and the deviations are plotted. The study shows that the improved model reflects the future trend of the development of maritime traffic safety index with a better accuracy and smaller deviation than the traditional model.

Keywords: maritime traffic safety index; improved grey prediction model; weakening operator; prediction; accuracy

根据交通运输部相关规定,一般使用水上交通事故起数、死亡失踪人数、沉船艘数和直接经济损失等4项绝对指标(简称“4项指标”)来反映辖区水域交通事故的规模、掌握事故情况、分析事故规律和总结经验教训，从而采取有效措施防止事故发生。因此,定量分析“4项指标”的发展趋势对控制海上交通风险、保障船舶安全航行具有重要意义。[1]目前针对海上交通安全的综合评价指数预测方法有很多，如时间序列预测法、博克斯-詹金斯法、事故死亡发生概率测度法和回归预测法等。研究发现,运用这些方法对实际问题进行预测存在一定的偏差，尤其是对波动性较大的数据预测精度不高。[2]对此，将弱化算子理论与灰色预测理论相结合，构造一种改进的弱化算子灰色预测模型，以历年“4项指标”数据为基础，依次对其进行传统灰色模型预测和改进灰色模型预测，最后比较分析2种预测模型的精度和拟合曲线。实践结果证明,改进后的预测模型精度更高、拟合度更好，整体上提高了预测的合理性和有效性。[3]

1 灰色预测模型的基本原理

建立灰色预测模型是将离散的原始数据转变为有规律的数列，对生成的数据序列建立预测模型，得到其预测值，通过对比实际值与预测值进行精度检验。若精度达到标准，则可进行事故预测；若精度未达到标准，则需对模型进行修改，重新进行精度检验，待达到精度要求时再进行预测。[4]

1.1建立灰色预测模型

设原始数据序列x(0)为

x(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(1)

式(1)中：x(0)(k)≥0,k=1,2,3,…,n。

对原始数据序列x(0)作1次累加(1-AGO)生成序列x(1)。[5]

x(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(2)

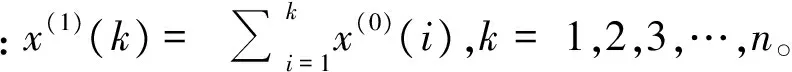
对x(1)紧邻数据求均值,生成序列z(1)。

z(1)=(z(1)(1),z(1)(2),…,z(1)(n))

(3)

x(1)序列具有近似指数变化规律，其白化形式的微分方程为

(4)

对x(1)采用最小二乘法确定加权模型GM(1,1)参数。

(5)

建立预测模型为

(6)

累减还原初始值为

x(0)(k+1)=x(1)(k+1)-x(1)(k)

(7)

1.2预测模型的精度检验

1.2.1残差e(0)和相对误差E的检验

(8)

(9)

残差越小，相对误差越小，模型精度越高。

1.2.2后验差检验

1.2.3绝对关联度

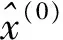
(10)

(11)

作1次累减得

(12)

式(12)中:k=1,2,…,n-1。计算各点的关联系数得

(13)

计算关联度得

(14)

关联度越大，精度越高。

预测模型精度由相对误差E，均方差比C，小误差概率p和关联度K共同决定，预测模型精度检验标准见表1。

表1 预测模型的精度标准

2 海上交通综合安全指数的改进灰色预测模型应用

以交通运输部每年公布的《交通运输行业发展统计公报》数据为基础，选取2004—2013年我国海上交通综合安全4项指标数据作为研究对象建立预测模型，利用预测模型对2014年的4项指标进行预测(见表2)。

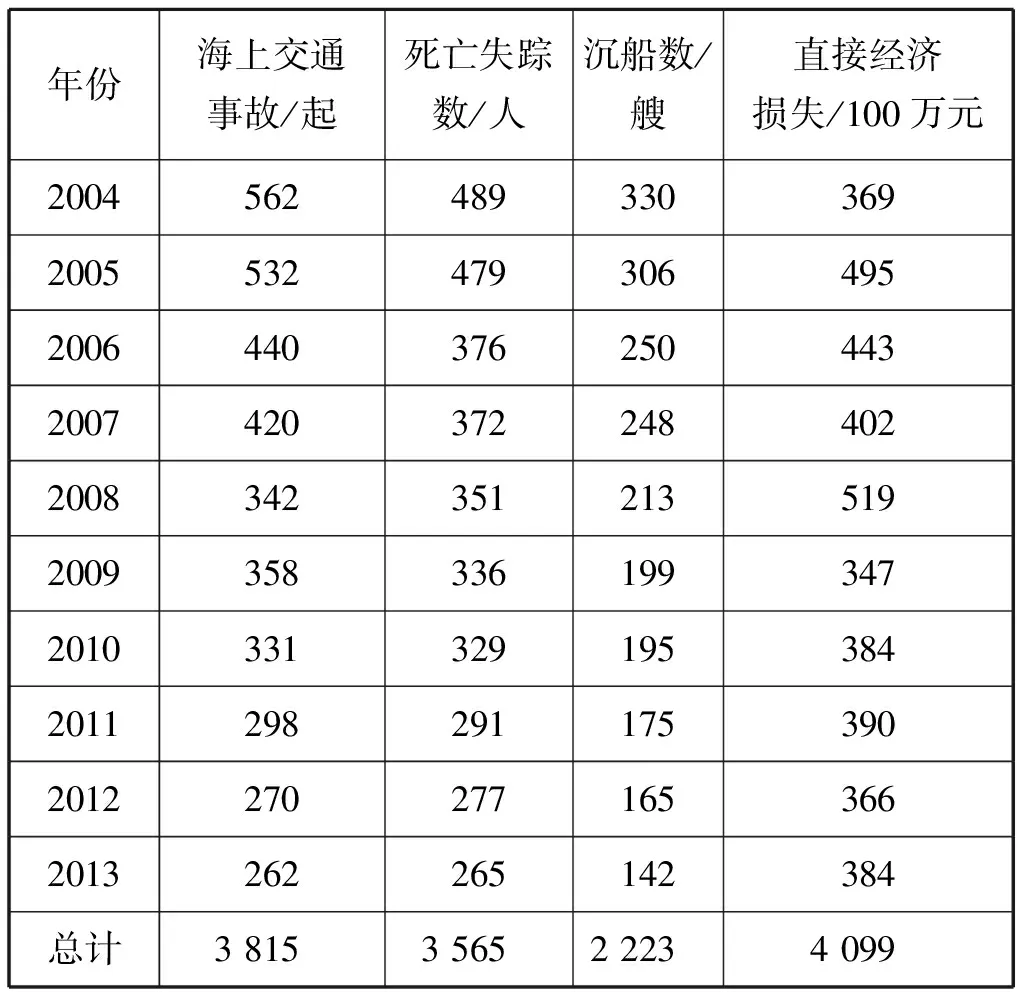
表2 2004—2013年4项指标数据

由表2可知,2004—2013年我国共发生海上交通事故3 815起，死亡失踪3 565人，沉船2 223艘，直接经济损失40.99亿元。从海上交通综合安全指数上看，4项指标的值整体上呈下降趋势，但直接经济损失呈折线型波动，且海上交通事故数及导致的沉船数和人员伤亡数仍较高，可见我国海上通航状况仍不容乐观。[8]

鉴于此，对海上交通综合安全4项指标采用2种不同的处理方法建立灰色预测模型，对比分析2种模型的精度和曲线拟合度，从而进一步提高预测精度，更好地保障海上交通安全。[9]

2.1根据原始数据直接建立模型(传统模型)

以2004—2013年的海上交通事故数作为原始数列,即x(0)=(562,532,440,420,342,358,331,298,270,262)。利用传统灰色预测模型进行计算,可得预测模型为

x(1)(k+1)=-5 929.88e-0.088k+6 491.88

(15)

对原始模型进行精度检验,相对误差E为0.037 4，精度标准为二级。

2.2改进弱化算子建立模型(改进灰色模型)

2.2.1改进弱化算子

在现有的弱化缓冲算子研究的基础上进行改

进，设原始数据序列为

x(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(16)

对原始数据序列进行改进弱化计算,得

XD1=[x(0)(1)d1,x(0)(2)d1,…,x(0)(n)d1]

(17)

(18)

设2004—2013年的海上交通事故原始序列为x(0)=(562,532,440,420,342,358,331,298,270,262)。进行改进弱化后得到数据序列为x(0)=(316,308,299,292,285,282,276,269,264,262)。

建立预测模型，求出累加序列为

x(1)(k+1)=-15 109.12e-0.020 4k+15 425.12

(19)

2.2.2对改进灰色模型进行精度检验

对改进灰色模型进行精度检验,结果见表3。

表3 预测精度检验

2.2.2.1 残差e(0)和相对误差E的检验

由原始数据序列和预测数据序列可得残差序列为e(0)=(0，2.553 4，-0.271 7，-1.221 6，-2.293 8，0.514 1，0.204 7，-1.219 8，-0.757 1，2.595 3)。

计算得到模型平均相对误差E=0.004 6<0.01，精度为一级。2.2.2.2 后验差检验

2.2.2.3 关联度计算

通过计算得关联系数序列为ξ=(0.990 6，0.990 6，0.996 8，0.996 8，0.990 6，0.996 8，0.996 8，0.996 8，0.987 5);γ=0.993 7>0.90，预测模型精度为一级。

综上所述，改进后的预测模型精度为一级，具有很好的参考价值。

同理,对死亡失踪人数、沉船数及直接经济损失进行传统模型和改进灰色模型的预测，相关数据见表4。

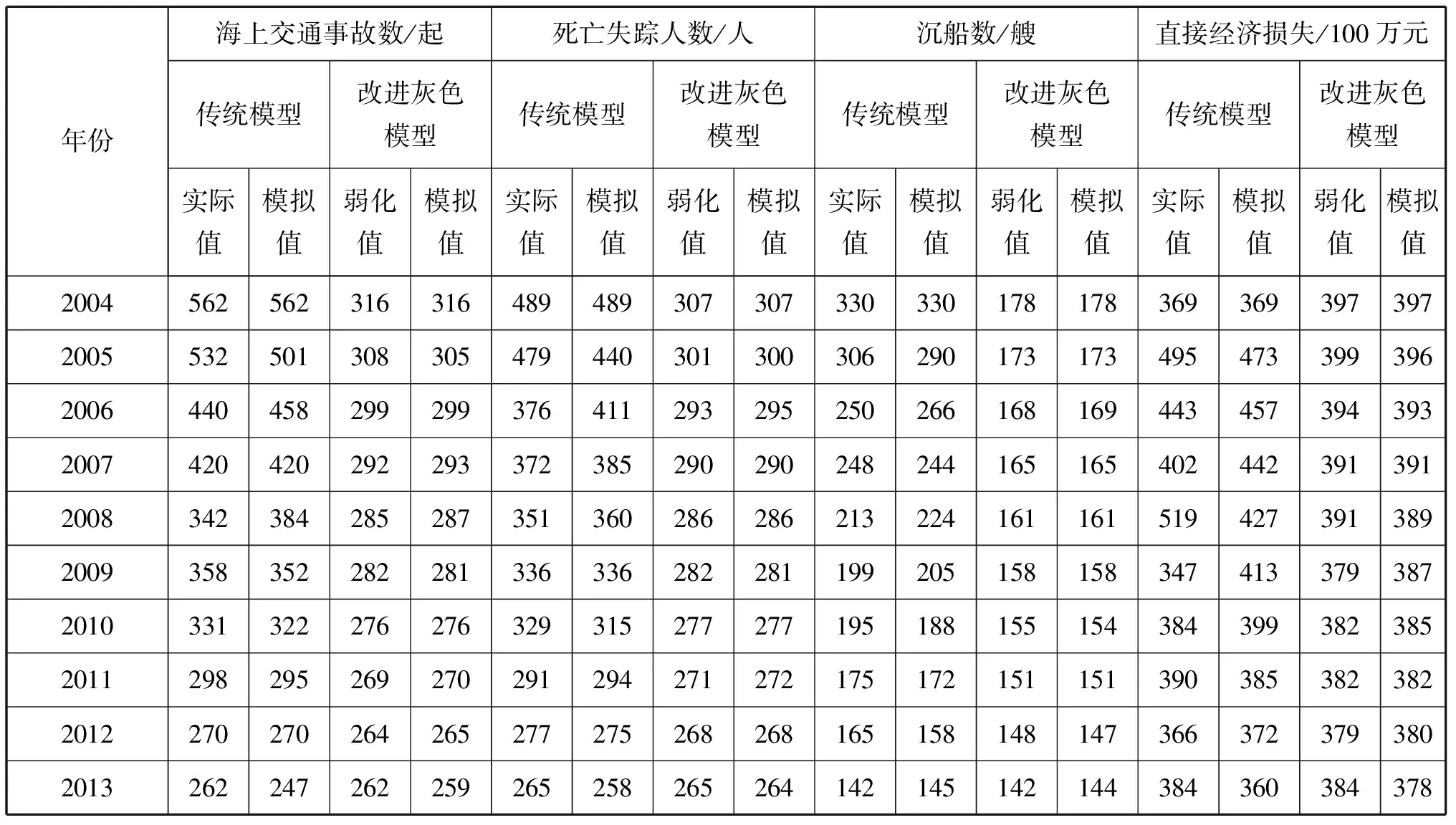
表4 2004—2013年我国海上交通综合安全指数模型相关数据

3 海上交通综合安全指数的预测结果比较分析

3.1预测结果

通过运用传统灰色预测模型和改进灰色预测模型对4项指标进行计算,得到相应的预测值如表2所示，检验预测模型的精度见图1。

3.1.1海上交通事故

(1) 传统模型：E=0.037 4;C=0.187 2;p=1;K=0.960 3;精度等级为二级。

(2) 改进灰色模型：E=0.004 6;C=0.085 8;p=1;K=0.993 7;精度等级为一级。

3.1.2死亡失踪

(1) 传统模型：E=0.036 2;C=0.248 6;p=1;K=0.961 1;精度等级为二级。

图1 传统模型与改进灰色模型精度比较

(2) 改进灰色模型：E=0.002 9;C=0.073 3;p=1;K=0.996 0;精度等级为一级。

3.1.3沉船

(1) 传统模型：E=0.036 3;C=0.153 5;p=1;K=0.962 7;精度等级为二级。

(2) 改进灰色模型：E=0.004 3;C=0.072 4;p=1;K=0.996 3;精度等级为一级。

3.1.4直接经济损失

(1) 传统模型：E=0.074 8;C=0.733 0;p=0.700;K=0.886 1;精度等级为四级。

(2) 改进灰色模型：E=0.006 9;C=0.485 9;p=0.800;K=0.990 6;精度等级为二级。

利用“4项指标”对2种模型的原始值(弱化值)和预测值进行曲线拟合(见图2和图3)，直观反映2种模型的曲线拟合度和关联度情况。[10]

a)交通事故b)死亡失踪c)沉船d)经济损失

图2 传统模型原始值和预测值的拟合曲线

3.2预测结果的比较与分析

1) 由以上分析可知，就海上交通综合安全4项指标而言，对比2种模型的精度检验值，传统模型的相对误差E大于改进灰色模型,传统模型的均方差比C大于改进灰色模型,传统模型的小概率误差p小于等于改进灰色模型,传统模型的绝对关联度K小于改进灰色模型,传统模型的精度等级小于改进灰色模型。由灰色模型检验标准可知：综合分析2种模型的预测精度，改进灰色模型>传统模型，可见改进灰色模型的精度相比传统灰色模型有很大提高。

2) 比较图2与图3可知： 对于海上交通事故,传统模型的预测值和真实值在2005年和2008年的差值较大，改进灰色模型的预测值和真实值基本一致； 对于死亡失踪,传统模型的预测值和真实值在2005年和2006年的差值较大，而改进灰色模型的预测值和真实值基本一致； 对于沉船,传统模型的预测值和真实值除2007年、2011年和2013年以外每年都有一定的差距，而改进灰色模型的预测值和真实值除2013年以外基本上一致； 对于直接经济损失,由于原始数据呈折线波动性变化，导致传统模型的预测值和实际值差距很大，而改进灰色模型的预测值和实际值除2005年、2009年和2013年以外，走势基本上一致。由此可见，改进灰色模型的精度更高、拟合度更好、实用性更广。

a)交通事故b)死亡失踪c)沉船d)经济损失

图3 改进灰色模型弱化值和预测值的拟合比较

3) 由表4和图1～图3的计算结果及拟合图像可知，改进灰色模型的精度和拟合度能满足海上交通综合安全指数的预测要求，该方法能很好地克服传统模型数据的离散性、随机性和模糊性，能在很少的信息量的基础上得到较高精度的预测值。

3.3改进预测模型的可行性分析

为验证利用改进灰色模型预测4项指标的可行性，按照改进灰色预测模型计算基本步骤，以2004—2013年的海上交通安全综合指数历史数据为原始数据序列，采用传统模型和改进灰色模型对2014年4项指标进行预测(见表5)。结果表明，改进预测模型4项指标预测精度较高，应用于海上交通综合指数预测具有一定的可行性。[11]

同理,以2004—2014年4项指标原始数据为基础，运用改进预测模型进行预测,得到2015年和2016年的预测值见表6。

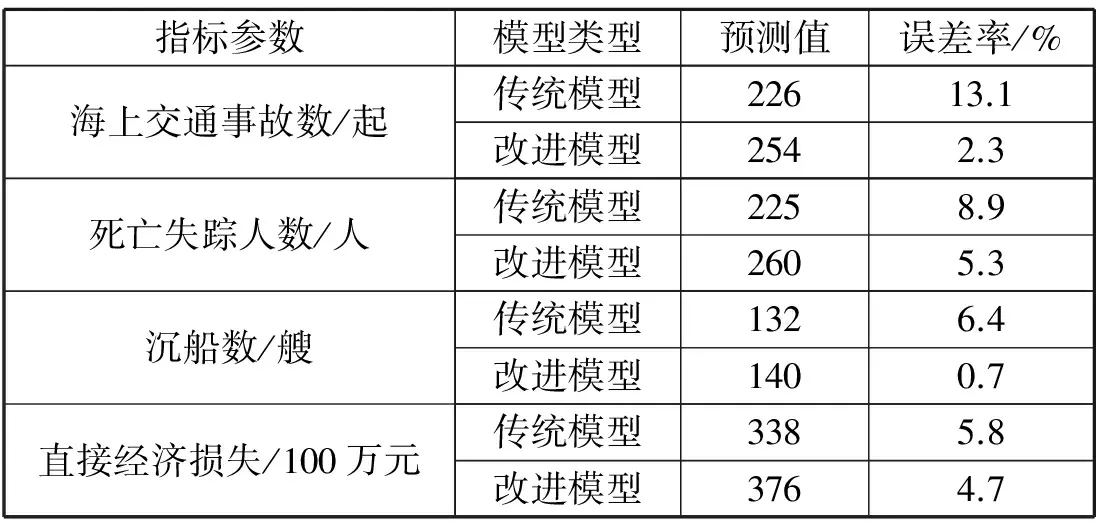
表5 2种模型预测精度比较

表6 改进灰色模型的海上交通综合安全4项指数预测

4 结束语

1) 对2004—2013年的海上交通综合安全指数历史数据进行2种模型预测分析，结果表明：改进预测模型的建模简单、易于实现，通过对比分析图可宏观看出4项指标的整体走势和波动变化，提高了模型的预测精度和拟合度，能很好地反映海上交通的实际情况。

2) 应用改进灰色模型进行预测时，需及时更新数据，以更好地对系统的变化趋势进行拟合。[12]

3) 通过对比分析2种预测模型4项指标的精度可知，相对于传统模型，改进后的模型预测精度更高，更适合描述随机波动性的数据序列，具有很好的普适性。

4) 灰色预测模型能反映辖区水上交通事故的总体发展趋势，弱化序列算子能很好地克服数据的波动性，两者的有机结合为海上交通事故的预测提供了新的方法和思路。

综上所述，改进后的预测模型实现了海上交通综合安全指数的准确预测，初步克服了传统灰色预测的局限性，很大程度上提高了模型的预测精度。由此可见，采用改进的灰色预测模型对海上交通综合安全指数进行预测具有一定的可行性。

[1] 王祺,王志明.马尔可夫灰模型的海上交通事故预测[J]. 中国航海,2013,36(4):119-124.

[2] 匡蕾,王斌.基于改进FNN的危险化学品运输事故智能预测[J].中国安全科学学报,2012,22(9):97-102.

[3] 刘敬贤,张涛,刘文.船舶交通流组合预测方法研究[J].中国航海,2009,32(3):80-84.

[4] 陈钊,徐阿猛.基于灰色马尔科夫模型的钻孔瓦斯流量预测[J].中国安全科学学报,2012,22(3):79-85.

[5] 张树奎,肖英杰.船舶交通流量预测的灰色神经网络模型[J].上海海事大学学报,2015,36(1):46-49.

[6] 苏梁,邵东,唐伯明,等.灰色理论在交通事故预测的应用[J].重庆交通大学学报(自然科学版),2008,27(3):446-448.

[7] 梅振国.灰色绝对关联度及其计算方法[J].系统工程,1992(5):43-44.

[8] 周涂强,吴超仲,张笛,等.基于改进综合安全指数的水上交通安全评价[J].中国航海,2015,38(2):69-73.

[9] 王宝阔.船舶交通事故量灰色预测应用研究[J].中国航海,2011,34(1):59-62.

[10] 刘雅君,罗文柯,唐如龙.单变量灰色预测模型在煤矿开采沉降预测中的对比分析[J].中国安全科学学报,2010,20(1):36-42.

[11] 魏家福,余建星,刘刚.航运市场预测方法研究[J].中国航海,2001，24(1):3-6.

[12] 陈海山,危强.灰色Verhulst模型在水上交通事故预测中的应用[J].中国航海,2013,36(2):67-69.

ImprovedGreyModelAppliedinMaritimeTrafficSafetyIndexPrediction

CHENChangyuan,DAIRan,FENGJijun,YUEXingwang,ZHANGJie

(Navigation College, Dalian Maritime University, Dalian 116026， China)

U698

A

2017-01-10

国家自然科学基金(61401057)；交通运输部应用基础研究项目(2014329225010)；马六甲和新加坡海峡超大型船舶航行风险分析及对策研究(01831508)；海上交通安全风险研究(80714003)

陈昌源(1989—)，男，山东济宁人，硕士生，从事交通信息工程及控制、水上交通安全保障方向研究。 E-mail: sunshineccy@126.com

1000-4653(2017)01-0058-06