轻量级分组密码算法ESF的安全性分析
尹 军 马楚焱 宋 健 曾 光 马传贵
1(数学工程与先进计算国家重点实验室(中国人民解放军信息工程大学) 郑州 450001)2(中国科学院信息工程研究所 北京 100093)3(中国科学院大学 北京 100049) 4(国防科学技术大学 长沙 410073)5(陆军航空兵学院 北京 101116) (yinjun66888@163.com)
2017-06-11;
2017-08-03
国家自然科学基金项目(61502532,61379150,61772519,61309016,61502529);数学工程与先进计算国家重点实验室开放基金课题(2016A02);河南省重点科技攻关计划项目(122102210126,092101210502) This work was supported by the National Natural Science Foundation of China (61502532, 61379150, 61772519, 61309016, 61502529), the Open Foundation of the State Key Laboratory of Mathematical Engineering and Advanced Computing (2016A02), and the Key Scientific and Technological Project of Henan Province (122102210126, 092101210502).
轻量级分组密码算法ESF的安全性分析
尹 军1,2,3马楚焱4宋 健1曾 光1马传贵5
1(数学工程与先进计算国家重点实验室(中国人民解放军信息工程大学) 郑州 450001)2(中国科学院信息工程研究所 北京 100093)3(中国科学院大学 北京 100049)4(国防科学技术大学 长沙 410073)5(陆军航空兵学院 北京 101116) (yinjun66888@163.com)
自动化分析是当前对密码算法进行安全性评估的重要方法之一,具有高效、易实现的特点.对面向位的分组密码,自从Sun等人在2014年亚洲密码年会上提出基于MILP问题的差分和线性自动化搜索方法,该方法受到了许多密码学者的关注.目前,针对求解多轮密码算法MILP模型,如何减少变量和约束不等式的研究工作相对较少,还有很多问题有待解决.根据异或操作的差分传播模式,在2017年欧洲密码年会上,Sasaki等人给出了不带假设变量的新约束不等式,该约束不等式在降低变量和约束数量的前提下保留了异或操作的差分传播性质.同时,对于S盒的性质,当输入差分变量(线性掩码)非零时,该S盒必定活跃,Sun等人用了4个约束不等式来刻画该性质,经过简单的变换,可以用1个约束来表示该性质.基于这些精炼的约束和自动化搜索方法,针对轻量级分组密码算法ESF,建立单密钥下精炼的差分和线性MILP模型,首次给出了ESF算法在单密钥情形下的差分和线性分析结果,得到了15轮ESF算法差分最小活跃S盒数量为19和16轮ESF算法线性最小活跃S盒数量为15.此外,还搜索到了轮数最长的不可能差分和零相关线性逼近区分器.
差分密码分析;线性密码分析;不可能差分;零相关线性逼近;ESF;MILP
当前,对于轻量级分组密码的设计与分析越来越受到人们关注,密码学者提出了许多轻量级分组密码算法,比较知名的算法有LBlock[1],PRESENT[2],SKINNY[3],RECTANGLE[4]等.
对分组密码2种经典的密码分析方法是差分密码分析[5]和线性密码分析[6].差分密码分析是1990年由Biham和Shamir提出的,他们利用这种方法攻击了DES密码算法,其主要思想是通过分析一个特选的明文对差分对相应密文对差分的影响来恢复密钥信息.差分攻击最重要的步骤是寻找高概率差分特征.线性密码分析是Matsui[6]在1993年的欧洲密码年会(欧密会)上提出来的,它属于已知明文攻击范畴,通过分析明密文之间的线性关系,构建明密文之间线性偏差不为0的线性逼近表达式,利用该线性逼近表达式来恢复密钥.此外,在上述2种密码分析方法的基础上,提出了许多扩展的密码分析方法,例如不可能差分密码分析[7]、零相关线性逼近[8]等,不可能差分密码分析的基本思想就是利用概率为零(或者非常小)的差分特征,排除那些导致差分概率为零(或者非常小)的差分特征对应的密钥.零相关线性逼近是由Bogdanov和Rijmen首次提出,通过寻找密码算法中相关度为零的线性逼近表达式,区分密码算法与随机置换,进行密钥恢复.
在上面2类密码分析方法中,寻找最优的差分特征和线性逼近是进行有效攻击的关键,其复杂度要低于暴力搜索.自动化分析是非常流行和高效的寻找最优差分和线性特征的方法,其主要思想是通过编程软件,自动化搜索差分和线性特征.目前,这类工作已经取得了很多成果,在1994年欧洲密码年会上,Matsui提出了分支定界搜索算法,搜索DES的差分特征[9];在2013年Mouha和Preneel构造了一个工具,基于可满足性模问题(satisfiability modulo theories, SMT),搜索流密码Salsa20的最优差分特征[10];此外,计算活跃S盒数量的下界是另外一种评估分组密码抵抗差分和线性分析的方法.在2011年Mouha等人将计算活跃S盒数量的问题转化成混合整数线性规划(mixed-integer linear programming, MILP)问题,应用于面向字的分组密码[11];在2014年亚洲密码年会上,Sun等人扩展了Mouha等人的方法,对面向位的分组密码,在单密钥和相关密钥模型建立MILP模型,分别计算最小活跃S盒数量的下界,搜索到了许多密码算法差分和线性特征[12];2016年Cui等人在差分和线性MILP方法基础上,实现了不可能差分和零相关线性逼近的自动化搜索[13].同时,在2017年欧洲密码年会上,Sasaki等人扩展MILP方法,提出了新的自动化搜索不可能差分的工具[14].
ESF[15]是刘宣等人基于吴文玲研究员的 LBlock 算法改进的轻量级分组密码算法,同时在置换层还采用了PRESENT算法的P置换形式,分组长度64 b,密钥长度80 b.针对ESF的密码分析,刘宣等人给出了ESF算法8轮不可能差分区分器来攻击11轮 ESF算法[16],攻击的数据和时间复杂度分别是259和275.5.随后,陈玉磊等人利用文献[16]中刘宣等人给出的8轮不可能差分区分器,根据轮密钥之间的关系,通过改变原有轮数扩展和密钥猜测的顺序,改进了11轮ESF的不可能差分攻击结果,攻击的数据和时间复杂度[17]分别是253和232.
本文的主要贡献有4个方面:
1) 根据Sasaki等人在2017年亚洲密码年会上给出的改进XOR操作约束*该约束出现在Sasaki等人在2017年欧洲密码年会上作的报告slide中,具体请参考https://eurocrypt2017.di.ens.fr/slides/A09-new-impossible-differential.pdf.,以及我们改变的S盒相关的约束,建立了更加精炼的MILP模型,大大减少了建立MILP模型的约束和变量数量;
2) 基于精炼的MILP模型,建立单密钥下ESF算法的差分和线性MILP模型,首次给出了ESF算法在单密钥情形下的差分和线性分析结果;
3) 基于精炼的MILP模型,建立ESF算法的不可能差分和零相关线性逼近MILP模型,给出了ESF算法的不可能差分和零相关线性分析结果.
4) 在输入输出差分只有一个活跃半字节的情形下,通过Gurobi软件求解该模型,搜索到了15轮ESF算法差分最小活跃S盒数量为19;在输入输出掩码只有一个活跃比特位的情形下,搜索得到16轮ESF算法线性最小活跃S盒数量为15.此外,我们还搜索到最长9轮的不可能差分和8轮的零相关线性区分器.具体的攻击结果如表1所示:

Table 1 The Attack Results for ESF
1 准备知识
本节首先给出常用的符号和术语说明,然后简要描述轻量级分组密码算法ESF.
1.1常用的符号和术语
Li:第i轮ESF算法输出的左32 b;
Ri:第i轮ESF算法输出的右32 b;
F:轮函数;
Ki:第i轮32 b子密钥;
ΔX:表示X1和X2的差分,X1⊕X2=ΔX;
<<<7:循环左移7 b.
1.2ESF算法
ESF算法是基于Lblock算法改进的轻量级分组密码算法,分组长度64 b,密钥长度80 b,迭代轮数为32轮.ESF算法采用广义的Feistel结构,轮函数为SPN结构.一轮的ESF加密流程如图1所示*图1和图2由TikZ for Cryptographers产生,具体详情请参考http://www.iacr.org/authors/tikz/..其中轮函数F为SPN结构,由非线性变换S函数和置换函数P组成,轮函数F如图2所示.轮函数F为F(Ri,Ki)=P(S(Ki⊕Ri)),其中的S函数是一个非线性变换,由8个并行的4×4的S盒构成,8个S盒的具体分布如表2所示.
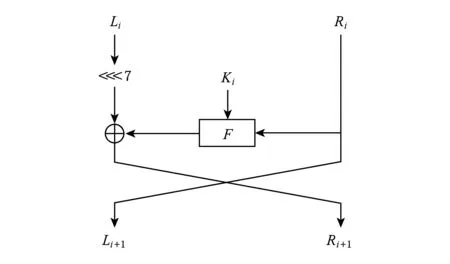
Fig. 1 1-round ESF encryption图1 1轮ESF加密过程
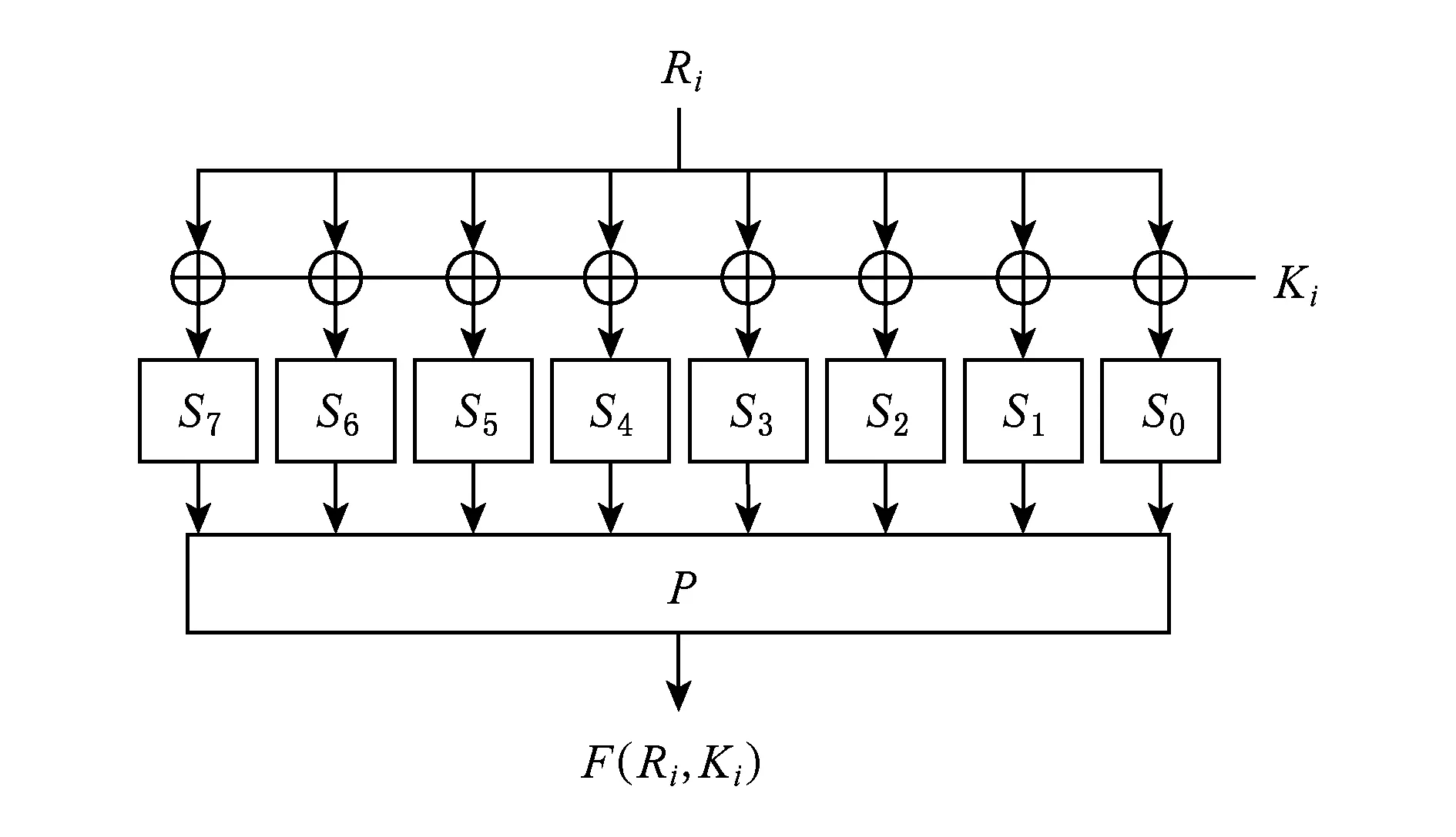
Fig. 2 The round function of ESF图2 ESF轮函数

Table 2 The S-Boxes of ESF
具体变换如下:
a=a7‖a6‖…‖a0→b=b7‖b6‖…‖b0,
b7=S7(a7),
b6=S6(a6),
b5=S5(a5),
b4=S4(a4),
b3=S3(a3),
b2=S2(a2),
b1=S1(a1),
b0=S0(a0).
P置换函数将32 b的(b31‖b30‖…‖b1‖b0)映射成(c31‖c30‖…‖c1‖c0),具体如下:
b=(b31‖b30‖…‖b1‖b0)→c=(c31‖c30‖…‖c1‖c0),当i=0,1,…,7时,
b4i‖b4i+1‖b4i+2‖b4i+3→ci‖ci+8‖ci+16‖ci+24.
在本文中,我们只考虑单密钥情形下的密码分析.因此对于密钥扩展算法,具体细节可参考文献[15].
2 基于MILP问题的自动化分析技术
在本节中,我们主要介绍MILP,后面详细介绍基于MILP模型自动化搜索差分特征、线性特征、不可能差分和零相关线性逼近,具体应用于ESF算法上产生约束不等式的过程.同时给出我们优化的MILP模型.
2.1混合整数线性规划(MILP)
MILP问题是运筹学中的一类优化问题,旨在线性约束条件下求解目标函数的最小值或最大值.目前,求解这类问题目前有很多成熟的商业软件,例如Gurobi[18],Cplex[19],MAGMA[20]等.下面具体给出MILP的定义.
定义1. MILP.假设A∈m×n,b∈m和c1,c2,…,cn∈n,寻找一个向量x=(x1,x2,…,xn),在相应的线性约束条件Ax≤b下求解线性函数c1x1+c2x2+…+cnxn的最小值或者最大值.
2.2建立改进的自动化搜索差分特征MILP模型
根据Sun等人对面向位的分组密码建立差分特征自动化搜索方法,通过对密码算法的每轮差分变量使用二元域上的0和1变量来描述,同时这些变量受限于密码算法特殊的操作和结构.根据文献[12,21],下面介绍建立ESF算法差分特征搜索MILP模型的过程.
在ESF算法中,一共包含4个操作:循环移位、P置换、XOR(异或)操作、S盒,其中循环移位和P置换,可以根据相应的比特位置给出等式约束.重点考虑2个操作:
首先对于S盒,引入新的0-1变量At表示S盒是否活跃,定义为
2.2.1 ESF算法XOR操作差分约束
假设XOR操作的输入差分分别为Δa和Δb,输出差分为Δc.其中Δa=(Δa0,Δa1,…,Δa31),Δb=(Δb0,Δb1,…,Δb31),Δc=(Δc0,Δc1,…,Δc31).同时对0≤i≤31,满足有Δai⊕Δbi=Δci.下面给出对异或操作差分约束:
(1)
其中,di是假设的0,1变量,0≤i≤31.
在2017年欧洲密码年会上,Sasaki等人针对XOR操作,改进了Sun等人给出的约束式(1).给出了不带假设的0-1变量约束式(2),对于ESF算法,每轮可以减少32个变量和32个约束.这样可以显著减少求解MILP模型的时间,提高效率,增加攻击轮数.
(2)
2.2.2 ESF算法S盒操作差分约束
假设(Δx0,Δx1,Δx2,Δx3)和(Δy0,Δy1,Δy2,Δy3)分别表示ESF算法4×4的S盒的输入和输出差分,At表示这个S盒是否活跃.
首先,为了保证Δx0,Δx1,Δx2,Δx3有任意一个是1时,At=1,用不等式约束:
我们通过分析上面的4个不等式,对其进行改进,使用1个不等式来表示这个约束条件:
Δx0+Δx1+Δx2+Δx3-4At≤0.
(3)
这样给出的约束不等式能够保证S盒差分传播的正确性,同时,在建立ESF算法的MILP模型中,每轮可以减少24个约束.
其次,当At=1时,Δx0,Δx1,Δx2,Δx3必定有一个非零,用不等式约束为
Δx0+Δx1+Δx2+Δx3-At≥0.
(4)
最后,对于双射的S盒,因为非零的输入差分必然导致非零的输出差分,反之亦然,用不等式约束为
(5)
除了式(3)~(5)对S盒差分的约束,Sun等人还提出了2套系统的方法,通过产生线性不等式来描述S盒的差分性质,使得刻画的S盒差分性质更加精确.这2种方法分别是逻辑状态模型和S盒所有可能差分模式的凸闭包H表示.对于第2种方法,在n维空间计算所有离散点的凸闭包H表示,通过SAGE中Sage.geometry.polyhedron类Inequality_generator()函数即可以得到凸闭包的H表示[22].但是,该函数产生的不等式非常多,对于ESF的每个S盒,都有大于300个不等式,因此要尽量减少不等式的数量,因此Sun等人设计了一个贪心算法来最大数量移除一部分不等式.表3给出了ESF算法8个S盒使用不同方法产生的不等式数量结果.
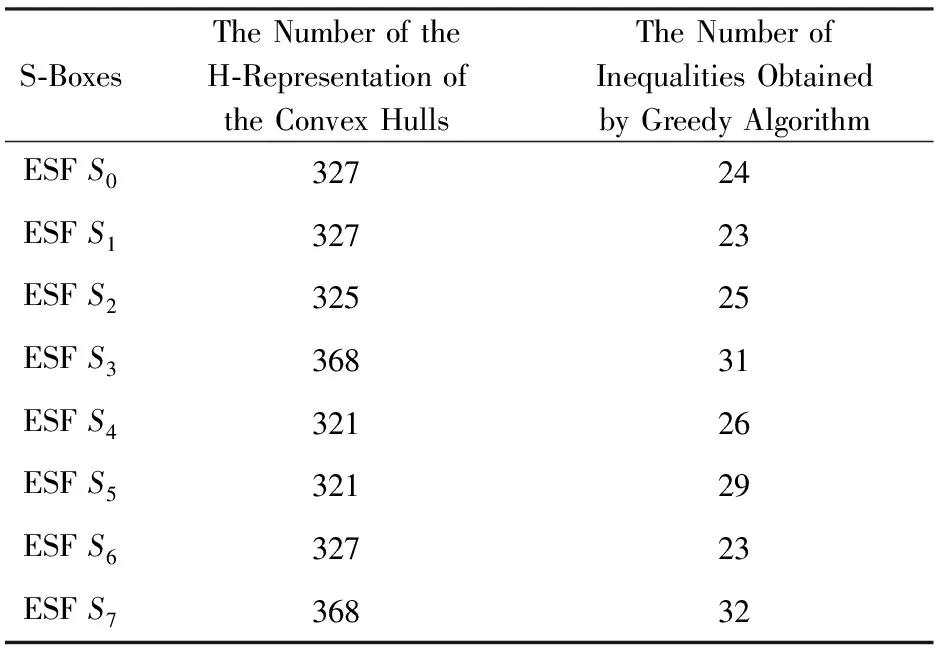
Table 3 The Number of Differential Inequalities Obtained by Different Methods
2.3建立自动化搜索线性特征MILP模型
为了自动化搜索ESF算法的线性特征,需要考虑ESF算法基本操作的线性掩码传播模式.因为位的旋转是一个简单的置换,可以根据相应的位给出等式约束,下面重点给出异或、分支和S盒操作的线性掩码传播约束.
首先对于S盒,引入新的0-1变量At表示线性活跃S盒,定义为
根据文献[12,21],下面具体给出对ESF算法操作的线性掩码变量约束.
2.3.1 ESF算法XOR操作线性掩码约束
假设ESF算法XOR操作中,a=(a0,a1,…,a31)和b=(b0,b1,…,b31)是异或操作的输入掩码,c=(c0,c1,…,c31)是其输出掩码,约束如下:
a=b=c.
2.3.2 ESF算法分支操作线性掩码约束
在ESF算法分支操作中,a=(a0,a1,…,a31)是输入掩码,b=(b0,b1,…,b31)和c=(c0,c1,…,c31)是输出掩码,约束如下:对0≤i≤31,ai⊕bi⊕ci=0,根据式(2),约束为
2.3.3 ESF算法S盒线性掩码约束
假设(x0,x1,x2,x3)和(y0,y1,y2,y3)分别表示ESF算法4×4的S盒的输入和输出掩码,At表示这个S盒是否活跃.
1) 为了保证输出掩码y0,y1,y2,y3有任意一个是1时,At=1,用不等式约束:
y0+y1+y2+y3-4At≤0.
(6)
2) 当At=1时,y0,y1,y2,y3必定有一个非零,用不等式约束:
y0+y1+y2+y3-At≥0.
(7)
3) 对于双射的S盒,因为非零的输入线性掩码必然导致非零的输出线性掩码,反之亦然,用不等式约束:
(8)
除了式(6)~(8)对S盒线性掩码的约束,计算S盒所有非零线性偏差线性掩码传播模式的凸闭包H表示,然后利用Sun等人给出的贪心算法来来选择最大数量移除不可能线性掩码模式不等式.通过不同方法产生的不等式数量结果如表4所示:

Table 4 The Number of Inequalities Obtained by Different Methods
对于异或操作约束、S盒操作约束、逻辑状态模型、凸闭包H表示、贪心算法,详细内容请参阅文献[12,21].
2.4建立自动化搜索不可能差分MILP模型
为了搜索ESF算法的不可能差分,根据Cui等人和Sasaki等人给出的自动化搜索不可能差分工具,只需要简单修改一下基于MILP模型的差分特征搜索工具,就可以得到自动化搜索不可能差分的MILP模型.
假设ΔI和ΔO分别表示输入和输出的差分,为了测试(ΔI,ΔO)是不可能的差分对,在建立的差分MILP模型中增加固定的输入和输出差分的某些比特作为约束,在该模型中不必考虑目标函数,如果MILP求解器输出错误信息(例如Gurobi输出infeasible),那么就可以知道这是一条不可能差分路径.
2.5建立自动化搜索零相关线性逼近MILP模型
基于MILP模型搜索零相关线性逼近,跟搜索不可能差分类似,只需要修改相应的线性特征MILP模型,就可以得到自动化搜索零相关线性逼近的MILP模型.
对于建立不可能差分和零相关线性逼近自动化分析MILP模型,详细内容请参阅文献[13-14].
3 轻量级分组密码ESF的安全性分析
根据第2节所叙,结合ESF算法的加密过程,用Python编程分别产生自动化搜索差分特征、线性特征、不可能差分和零相关线性逼近“lp”文件格式的MILP模型,并且调用Gurobi7.0.2来求解相应的MILP模型.求解MILP模型的实验环境在一台服务器上进行,该服务器配置如表5所示:

Table 5 Experimental Environment for Solving MILP Model
3.1ESF算法差分分析结果
通过建立r轮ESF算法的差分MILP模型,可以知道产生的差分MILP模型有373r+1个不等式、72r+64个变量,ESF算法前15轮在单密钥情形下差分活跃S盒数量的下界,如表6所示:
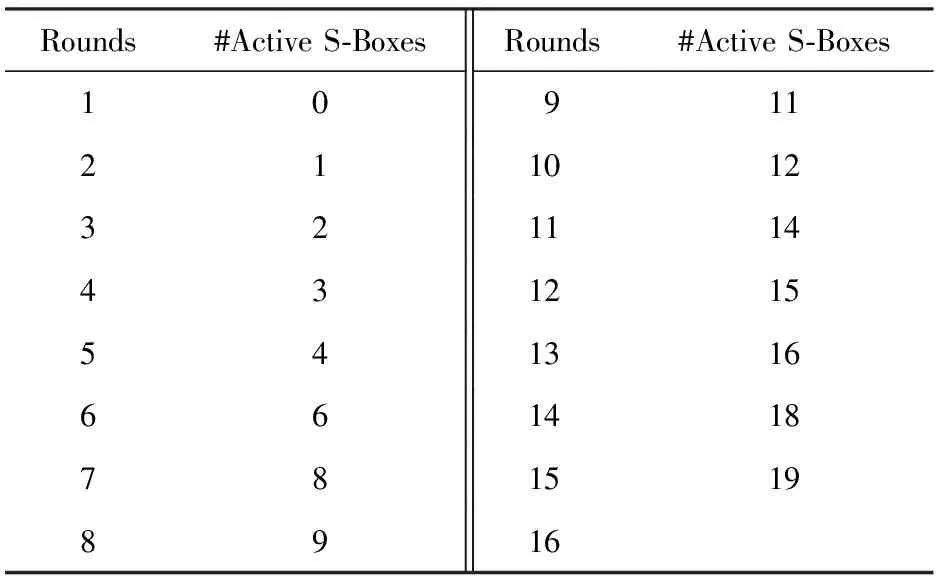
Table 6 The Results for Single-key Differential Analysis on ESF
从表6我们知道对于15轮的ESF算法最小差分活跃S盒数量是19.对于超过15轮的模型,由于求解花费的时间关系(超过15 d),我们只考虑前15轮的模型.因为ESF算法S盒的最优差分概率是2-2,估计全轮(32=15+15+2)的ESF最大差分概率是(2-2)19+19+1=2-78,小于暴力搜索成功的概率2-64.因而,我们证明ESF对单密钥差分攻击是安全的.
3.2ESF算法线性分析结果
建立r轮ESF算法的线性MILP模型,对于r轮ESF算法,线性MILP模型有421r+1个不等式、104r+64个变量.ESF算法前16轮在单密钥情形下线性活跃S盒数量的下界,如表7所示.
从表7可知,对于16轮的ESF算法最小线性活跃S盒数量是15.对于超过16轮的模型,跟ESF算法差分分析一样,由于求解模型花费的时间关系(超过12 d),我们只考虑前16轮的模型.因为ESF算法S盒的最大线性偏差为ε=±2-2,估计全轮(32=16+16)的ESF最小活跃S盒数量为30(实际的大于30),由堆积引理[6],最大线性偏差的平方为ε2=2-58,那么对全轮的线性攻击需要已知的明文量约为258,小于暴力搜索需要的明文量264.但是,实际所需要的明文量肯定比258大,是否存在全轮活跃S盒数小于32的线性路径仍然不能确定.因而,对于证明全轮ESF是否抵抗线性攻击仍然是一个开放问题.

Table 7 The Results for Linear Analysis on ESF
3.3ESF算法不可能差分分析结果
根据2.4节自动化搜索不可能差分方法,建立r轮ESF算法的不可能差分MILP模型.即在相应的差分MILP模型的基础上增加2个约束,分别将输入和输出差分的1个半字节位置固定为常数,其他位置为0,并计算模型是否有解,总共需要遍历(16×16)2=216种情形.共搜索到2 108条9轮ESF的不可能差分,没有搜索到10轮的不可能差分.其中7条如下所示(输入输出数值用16进制表示):

3.4ESF算法零相关线性逼近分析结果
根据2.5节自动化搜索零相关线性逼近的方法,建立r轮ESF算法的零相关线性逼近MILP模型,对于每轮的MILP模型,分别在相应的线性MILP模型基础上增加了2个约束,分别是固定输入和输出掩码的1个比特位置为1,其他位全为0,总共需要遍历642=4096种情形.共搜索到925条8轮的零相关线性逼近,在此条件下,没有搜索到9轮的零相关线性逼近.其中的7条如下所示(输入输出数值用16进制表示):

4 结束语
在本文中,基于Sun等人给出的差分和线性自动化搜索方法,根据Sasaki等人改进的XOR操作约束和我们改进的S盒相应的约束,进一步精炼MILP模型,减少了ESF算法产生MILP模型的变量和约束数量,使得MILP问题的求解更加高效.我们将优化的MILP模型应用到轻量级分组密码算法ESF,在单密钥情形下成功获取了减轮ESF算法的差分和线性最小活跃S盒数量,并搜索到最长的不可能差分和零相关线性区分器.同时,证明了全轮ESF足够抵抗差分攻击,然而对于证明全轮ESF是否抵抗线性攻击仍然是一个开放问题.
[1] Wu Wenling, Zhang Lei. LBlock: A lightweight block cipher[G] //LNCS 6715: Proc of the 9th Int Conf on Applied Cryptography and Network Security (ACNS 2011). Berlin: Springer, 2011: 327-344
[2] Bogdanov A, Knudsen L R, Leander G, et al. PRESENT: An ultra-lightweight block cipher[G] //LNCS 4727: Proc of the 9th Int Workshop on Cryptographic Hardware and Embedded Systems (CHES 2007). Berlin: Springer, 2007: 450-466
[3] Beierle C, Jean J, Kölbl S, et al. The SKINNY family of block ciphers and its low-latency variant MANTIS [G] //LNCS 9815: Advances in Cryptology (CRYPTO 2016). Berlin: Springer, 2016: 123-153
[4] Zhang Wentao, Bao Zhenzhen, Lin Dongdai, et al. RECTANGLE: A bit-slice lightweight block cipher suitable for multiple platforms [J]. Science China Information Sciences, 2015, 58(12): 1-15
[5] Biham E, Shamir A. Differential cryptanalysis of DES-like cryptosystems [G] //LNCS 537: Advances in Cryptology(CRYPT0 1990). Berlin: Springer, 1990: 2-21
[6] Matsui M. Linear cryptanalysis method for DES cipher [G] //LNCS 765: Advances in Cryptology (EUROCRYPT 1993). Berlin: Springer, 1993: 386-397
[7] Biham E, Biryukov A, Shamir A. Cryptanalysis of skipjack reduced to 31 rounds using impossible differentials [G] //LNCS 1592: Advances in Cryptology (EUROCRYPT 1999). Berlin: Springer, 1999: 12-23
[8] Bogdanov A, Rijmen V. Linear hulls with correlation zero and linear cryptanalysis of block ciphers [J]. Designs Codes & Cryptography, 2014, 70(3): 369-383
[9] Matsui M. On correlation between the order of S-boxes and the strength of DES[G] //LNCS 950: Advances in Cryptology (EUROCRYPT 1994). Berlin: Springer, 1994: 366-375
[10] Mouha N, Preneel B. Towards finding optimal differential characteristics for ARX: Application to Salsa20[EB/OL]. [2017-06-11]. http://eprint.iacr.org/2013/328.
[11] Mouha N, Wang Qingju, Gu Dawu, et al. Differential and linear cryptanalysis using mixed-integer linear programming[G] //LNCS 7537: Proc of the 7th Int Conf on Information Security and Cryptology (Inscrypt 2011). Berlin: Springer, 2011: 57-76
[12] Sun Siwei, Hu Lei, Wang Peng, et al. Automatic security evaluation and (related-key) differential characteristic search: Application to SIMON, PRESENT, LBlock, DES(L) and other bit-oriented block ciphers[G] //LNCS 8873: Advances in Cryptology (ASIACRYPT 2014). Berlin: Springer, 2014: 158-178
[13] Cui Tingting, Jia Keting, Fu Kai, et al. New automatic search tool for impossible differentials and zero-correlation linear approximations[EB/OL]. [2017-06-08]. https://eprint.iacr.org/2016/689
[14] Sasaki Y, Todo Y. New impossible differential search tool from design and cryptanalysis aspects[G] //LNCS 10212: Advances in Cryptology (EUROCRYPT 2017). Berlin: Springer, 2017: 185-215
[15] Liu Xuan, Zhang Wenying, Liu Xiangzhong, et al. Eight-sided fortress: A lightweight block cipher [J]. Journal of China Universities of Posts and Telecommunications, 2014, 21(1): 104-108
[16] Liu Xuan, Liu Feng, Meng Shuai. Impossible differential cryptanalysis of lightweight block cipher ESF [J]. Computer Engineering & Science, 2013, 35(9): 89-93 (in Chinese)
(刘宣, 刘枫, 孟帅. 轻量级分组密码算法ESF的不可能差分分析[J]. 计算机工程与科学, 2013, 35(9): 89-93)
[17] Chen Yulei, Wei Hongru. Impossible differential cryptanalysis of ESF [J]. Computer Science, 2016, 43(8): 89-91 (in Chinese)
(陈玉磊,卫宏儒. ESF算法的不可能差分密码分析[J]. 计算机科学, 2016, 43(8): 89-91)
[18] Gurobi. Gurobi optimizer reference manual[EB/OL]. [2017-06-03]. http://www.gurobi.com
[19] IBM. User-Manual CPLEX 12[EB/OL]. [2017-06-03]. https://www-01.ibm.com/software/commerce/optimization/cplex-optimizer/index.html
[20] Computational Algebra Group. School of Mathematics and Statistics, University of Sydney: Magma Computational Algebra System[EB/OL]. [2017-06-03]. http://magma.maths.usyd.edu.au
[21] Sun Siwei, Hu Lei, Song Lin, et al. Automatic security evaluation of block ciphers with S-bP structures against related-key differential attacks[G] //LNCS 8567: Proc of the 9th Int Conf on Information Security and Cryptology (Inscrypt 2013). Berlin: Springer, 2013: 39-51
[22] Stein W. Sage Tutorial v8.0[EB/OL]. [2017-05-23]. http://doc.sagemath.org/html/en/tutorial/tour.html
SecurityAnalysisofLightweightBlockCipherESF
Yin Jun1,2,3, Ma Chuyan4, Song Jian1, Zeng Guang1, and Ma Chuangui5
1(StateKeyLaboratoryofMathematicalEngineeringandAdvancedComputing(PLAInformationEngineeringUniversity),Zhengzhou450001)2(InstituteofInformationEngineering,ChineseAcademyofSciences,Beijing100093)3(UniversityofChineseAcademyofSciences,Beijing100049)4(NationalUniversityofDefenseTechnology,Changsha410073)5(ArmyAviationInstitute,Beijing101116)
Automatic analysis is one of the important methods to evaluate the security of cryptographic algorithms. It is characterized by high efficiency and easily implement. In ASIACRYPT 2014, Sun et al. presented a MILP-based automatic search differential and linear trails method for bit-oriented block ciphers, which has attracted the attention of many cryptographers. At present, there are still a lack of research about solving the MILP model, such as how to reduce the number of variables and constraint inequalities. According to the differential propagation model of the XOR operation, in EUROCRYPT 2017, Sasaki et al. gave a set of new constraints without dummy variables. The new constraint inequalities can not only preserve the differential propagation for XOR operation, but also reduce the number of variables. At the same time, Sun et al. uses four constraints to describe the property when the input differential variable (the linear mask variable) of an S-box is non-zero and the S-box must be an active, but in this paper, we just use one constraint. Based on these refined constraints and the automatic method for finding high probability trails of block cipher, we establish the refined differential and linear MILP model under the single key assumption for the lightweight block cipher ESF. We have found that the minimum number of active S-boxes in 15-round differential trail of ESF is 19 and the number is 15 in 16-round linear trail. Moreover, we find so far the longest impossible differential and zero-correlation linear approximation distinguishers of ESF.
differential cryptanalysis; linear cryptanalysis; impossible differential; zero-correlation linear approximation; ESF; MILP
TP309.7

YinJun, born in 1993. Master candidate. His main research interests include automatic analysis of cryptographic algorithms.

MaChuyan, born in 1994. Master candidate. His main research interests include automatic analysis of block ciphers.

SongJian, born in 1993. Master candidate. His main research interests include security analysis of cryptographic protocols.

ZengGuang, born in 1980. PhD, associate professor. His main research interests include security analysis of Hash function.

MaChuangui, born in 1962. Professor and PhD supervisor. His main research interests include network and information security.

