可修订数字签名研究综述

马金花 刘江华 伍 玮 黄欣沂

1(福建师范大学数学与信息学院 福州 350007) 2(福建省网络安全与密码技术重点实验室(福建师范大学) 福州 350007) 3(澳大利亚迪肯大学信息技术学院 澳大利亚墨尔本 3125) (jinhuama55@hotmail．com)

2017-09-01；

2017-09-05

国家自然科学基金项目(61402110,61472083,61771140)；福建师范大学校创新团队基金项目(IRTL1207)；福建省杰出青年科学基金项目(2016J06013) This work was supported by the National Natural Science Foundation of China (61402110, 61472083, 61771140), the Innovation Team of Fujian Normal University (IRTL1207), and the Distinguished Young Scholars Fund of Fujian Province (2016J06013).

伍玮(weiwu@fjnu.edu.cn)

可修订数字签名研究综述

马金花1,2刘江华3伍 玮1,2黄欣沂1,2

1(福建师范大学数学与信息学院 福州 350007)2(福建省网络安全与密码技术重点实验室(福建师范大学) 福州 350007)3(澳大利亚迪肯大学信息技术学院 澳大利亚墨尔本 3125) (jinhuama55@hotmail．com)

数据的安全问题已成为关系国家经济、政治、国防、文化安全的重大问题.数字签名可验证数据内容的完整性和数据源的真实性，是保障数据安全的核心技术之一.数字签名的传统安全要求为在自适应选择消息攻击下满足存在不可伪造性.虽然数字签名的传统安全目标能满足数据认证的基本要求，但也阻碍了对已签名数据的合理操作，不能满足很多实际应用的需求.可修订签名是一类支持编辑操作的具有同态性质的数字签名.在不与签名人交互的情况下，签名持有人(修订者)可删除已签名数据中的敏感子数据，并计算修订后数据的有效签名.自2001年可修订数字签名被正式提出以来，就一直是应用密码学领域的研究热点.近年来许多国内外的学者从形式化安全定义、修订规则、计算效率、通信效率等多个方面对其进行探索研究，相继取得了一批有意义的研究成果.网络技术及其应用的快速发展在不断地对可修订数字签名提出新的要求，将从其核心算法定义、安全模型以及现有的代表性方案等方面对可修订数字签名进行概括和分析，并探讨值得进一步研究的问题.

可修订签名；同态签名；数字签名；数据认证；安全模型

随着社会的日益数字化，人类社会已经进入数据时代，数据的价值得到越来越广泛的认同，数据的安全问题已成为关系国家经济、政治、国防、文化安全的重大问题[1].Diffie和Hellman[2]于1976年首次提出公钥密码学(public key cryptography, PKC)的概念，开创了密码学和网络信息安全发展的新纪元[3].数字签名(digital signatures)可验证数据内容的完整性和数据源的真实性，是一种重要的公钥密码技术，也是保障数据安全的核心工具之一[4].

数字签名的传统安全要求为在自适应选择消息攻击下满足存在不可伪造性(existential unforgeability under adaptive chosen message attacks, EUF-CMA)[5].EUF-CMA要求：已知公钥pk，概率多项式时间(probability polynomial-time, PPT)攻击者在获得它希望得到的有效数据签名后，能够为新数据M*计算出有效签名的概率是可忽略的.如果数字签名方案满足上述安全要求，那么有效的数字签名能让数据接收者相信其收到的数据没有被篡改，且数据的发送方就是相应公钥pk的拥有者.

虽然数字签名的传统安全目标能满足数据认证的基本要求，但也阻碍了对已签名数据的合理操作，不能满足很多实际应用的需求.在电子商务、政府文件发布、智能电网、电子医疗记录等应用中，因为隐私保护或带宽节省等原因，签名持有人需要对已签名数据进行合理的修订.以电子医疗记录为例，电子医疗记录(electronic medical record)是一种新型的健康数据管理模式，其核心内容是用户的健康数据[6]，包含大量个人信息，如M= {姓名,性别,身份证号码,住址,联系电话,病情描述1,病情描述2,……,病情描述n,处方}，与个人的隐私密切相关.多国的法律法规明确规定电子医疗记录的使用要注意病人的隐私保护[7].以科学研究为目的的数据使用并不需要知道患者的真实姓名、身份证号码等信息，使用时应将这些敏感个人隐私数据从患者健康数据中删除.这称为数字文档净化(digital documents sanitizing)[8].

使用具有EUF-CMA性质的数字签名虽可保障原始数据的完整性，但无法得到净化后数据的签名.为了获得净化后数据的有效数字签名，数据持有人可将净化后的数据发给签名人，签名人在核对后对净化后的数据重新签名.该过程需要数据持有人和签名人进行多次交互，不仅计算代价大，而且在签名人离线的情况下，很难实现实时交互.签名人还可以预先对所有子数据的组合分别进行签名，该过程虽然避免了签名持有人和签名人之间的多次交互，但计算开销大且无法控制数据持有人对数据的恶意修订等行为.

同态数字签名为上述问题提供了有效的解决方案.图灵奖获得者Rivest教授在2001年的学术演讲中提出了同态数字签名(homomorphic signatures)的雏形[9].同态数字签名不满足传统的安全目标EUF-CMA，在不知道签名人私钥的情况下，允许签名持有人对已签名数据进行合理的授权操作，计算出新数据的有效签名.例如⊗,⊕是2个二元运算，签名人的私钥是sk，y和y′分别是数据x和x′的签名.在不知道私钥sk的情况下，第三方可以直接计算出新数据x*的同态签名y*，即y*=Sig(sk,x*)，其中y*=y⊗y′,x*=x⊕x′.在同态数据签名中，对已认证数据的合理操作不需要私钥等私密信息，支持外包计算，计算资源/通信资源有限的实体可将这些操作委托给第三方，符合云计算和物联网的特点，可以有效地解决上述的认证数字文档净化问题[8]，在电子投票、智能电网、电子医疗记录系统等很多实际场合有着广泛的应用[10-11].

可修订签名(redactable signatures)是一类支持编辑操作的具有同态性质的数字签名，其概念是由Johnson等人[12]于2002年正式提出，但Steinfeld等人[13]于2001年就已经提出了与可修订数字签名具有类似功能的数字签名，称为内容可截取签名(content extraction signature, CES).在不与签名人交互的情况下，签名持有人(修订者)可删除已签名数据中的敏感子数据，并计算修订后数据的有效签名.以集合型数据为例，设σ为集合型数据M={m1,m2,m3,m4,m5}的有效签名，修订者可以移除集合M的某个子集(如{m3,m4,m5})，并为余下的数据(即M′={m1,m2})计算有效签名σ′.该修订操作不需要签名人的帮助，修订者可独立完成.可修订签名要求得到的修订签名σ′不泄露被移除元素(即{m3,m4,m5})的任何信息.文献[13]设定了修订控制规则以限制签名持有人的修订行为，任何不符合修订规则的操作很难计算出有效签名，避免了因不合理或恶意的修订操作所导致的信息歧义、改变原意等情况的发生.除了集合型数据，可修订数字签名也支持字符串、树型以及图型等数据的修订操作.

自2001年被正式提出以来，同态数字签名引起了学术界的极大关注，一直是密码学与信息安全领域的研究热点.可修订数字签名作为一类支持编辑操作的具有同态性质的数字签名，近年来被许多国内外的学者从形式化安全定义、提取规则、计算效率、通信效率、签名更新等多个方面对其进行探索研究，相继取得了一批有意义的研究成果[12-48].但是网络技术及其应用的快速发展在不断地对可修订数字签名提出新的要求，本文将从其核心算法定义、安全模型以及现有的代表性方案等方面对可修订数字签名进行概括和分析，并探讨值得进一步研究的问题.

1 可修订数字签名

现有的可修订数字签名方案(redactable signa-ture schemes, RSSs)大都针对某一特定的数据结构设计，比如集合型数据[12-18]、链表型数据[19-25]、树型数据[26-36]、图型数据[37-43]等，相关的定义和安全模型也不相同.在现实生活中数据的存在形式多种多样，每一种数据的存储方式以及数据块之间的组合形式不尽相同，Derler等人[15]于2015年提出首个适用于多样化数据结构的可修订数字签名的一般架构模型，并给出了相应的安全性定义.为了便于理解，本节将基于文献[15]以集合型数据为例定义可修订签名.

1.1可修订签名定义

可修订签名由4个核心的有效算法构成：

1) 密钥生成算法KeyGen.输入系统安全参数λ，该概率性算法输出签名人的公私钥对(pk,sk).

2) 签名生成算法Sign.输入签名人私钥sk、数据M和修订控制规则ADM，该算法输出数据签名对(M,σ).

3) 签名修订算法Redact.输入签名人公钥pk、数据签名对(M,σ)和修订指令MOD，该算法输出修订后的数据签名对(M′,σ′).

4) 签名验证算法Verify.输入签名人公钥pk和数据签名对(M,σ)，该确定性算法输出一个比特值b∈{0,1}.当检验签名有效时，b=1；否则，b=0.

1.2可修订签名安全模型

不可伪造性(unforgeability)和隐私性(privacy)是可修订签名的2个基本安全要求，相应的形式化安全模型最早由Brzuska等人[28]提出.本节将基于文献[28]的安全模型，描述这2个安全要求.

1.2.1 不可伪造性

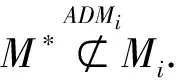
可修订签名的不可伪造性可用下面的挑战者C和攻击者A之间的游戏Game 1来刻画：

1) 挑战者C运行密钥生成算法(pk,sk)←KeyGen(1λ)，将公钥pk公开.

2) PPT攻击者A可自适应地选择q个数据(Mi,ADMi)询问签名预言机，并得到有效数据签名对(Mi,σi)，其中1≤i≤q.

3) 攻击者A输出数据签名对(M*,σ*).

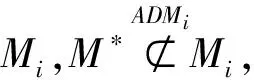
定义1. 不可伪造性.在适应性选择消息攻击下，如果任何PPT攻击者在游戏Game 1中获胜的概率是可忽略的，我们就称该可修订签名算法在适应性选择消息攻击下满足存在不可伪造性.

1.2.2 隐私性

在已知签名人公钥pk的情况下，PPT攻击者可以自适应地询问签名预言机，可修订签名的隐私性要求攻击者很难推导出被移除数据的信息.

可修订签名的隐私性可用下面的挑战者C和攻击者A之间的游戏Game 2来刻画：

1) 挑战者C运行密钥生成算法(pk,sk)←KeyGen(1λ)，将公钥pk公开.

2) PPT攻击者A可自适应地询问签名预言机.最后攻击者A选择2个数据{(M0,ADM0,MOD0),(M1,ADM1,MOD1)}发送给挑战者C，数据满足M0≠M1,M0MOD0=M1MOD1.

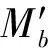
4) 攻击者A依然可自适应地询问签名预言机.最后攻击者A输出b*.如果b=b*则说明攻击者A在游戏Game 2中获胜；否则，攻击者A失败.

设Pr[A]为攻击者A在Game 2中获胜的概率，则A的优势Adv[A]=|Pr[A]-12|.

定义2. 隐私性.若PPT攻击者在游戏Game 2中的优势Adv[A]是可忽略的，我们就称该可修订签名算法满足隐私性要求.

1.2.3 其他安全要求

除了上述2个最基本的安全要求，面向特定应用的可修订签名还需要满足其他安全要求，包括透明性(transparency)[14-15]、不可链接性(unlinkability)[44-45]、可审计性(accountability)[22,46]和可合并性(mergeability)[19,24]等.以集合型数据M={m1,m2,m3,m4,m5}为例，原有效数据签名对为(M,σ).设(M1,σ1)和(M2,σ2)是(M,σ)的2个有效修订签名，分别由修订者R1和修订者R2执行修订操作得到，其中M1={m1,m2,m3}，M2={m3,m4,m5}.PPT攻击者A可自适应地询问签名预言机.

可修订签名算法的透明性要求：已知(M1,σ1)，攻击者很难判断(M1,σ1)是原始签名还是修订后的签名.

可修订签名算法的不可链接性要求：已知(M1,σ1)和(M2,σ2)，攻击者无法确定它们是否是从同一个原始签名(M,σ)修订得到的.

可修订签名算法的可审计性要求：已知(M1,σ1)，审计者可以断定(M1,σ1)是由修订者R1执行修订操作得到的.

可修订签名算法的可合并性要求：已知(M1,σ1)和(M2,σ2)，修订者可以计算出(M,σ).

因为只有特定应用环境下的可修订签名才应具有这些安全性要求，所以本节省略这些安全性能的形式化定义.

2 可修订数字签名代表性方案

现有的可修订数字签名方案主要是基于不同的密码学工具设计的，如基于向量承诺(CommitVector)的RSS[12,15,17,27]、基于Merkle Hash树的RSS[13,21,23,26-27,29,33-34,40]、基于双线性映射(bilinear mapping)的RSS[18,24-25,31-32]以及基于聚合器(accumulator)的RSS[14-15,19,47-48].本节将分别选取一个代表性的方案介绍上述4类RSS的设计思路.

2.1基于向量承诺(CommitVector)的CES方案[13]

Steinfeld等人[13]于2001年提出内容可截取签名(CES)的概念，是早期可修订数字签名的代表性方案之一.该方案针对有序集合数据，利用内容截取访问结构(content extraction access structure, CEAS)实现对签名持有人截取权限的限制.CEAS定义了原数据集合中可被截取的数据子集，与1.1节定义的ADM功能相同.以有序数据集合M={m[1],m[2]}为例，若每个子数据都可被截取，则M中允许截取的数据子集数目共有4=22个，分别为{∅},{m[1]},{m[2]},{m[1],m[2]}，CEAS(或ADM)即为这4个子集的集合，最多共有16=24种集合情况.如果原数据共有n个子数据，那么CEAS最多共有22n种形式.CEAS和ADM都可以有效地防止签名持有人不合理或恶意使用签名等情况的发生.

基于向量承诺的CES方案[13]由4个算法构成：

1) 密钥生成算法KeyGen(λ).输入系统安全参数λ，调用标准数字签名的密钥生成算法，输出公私钥对(sks,pks)；调用消息承诺方案的参数初始化算法，输出方案的参数字符串sp.最后输出CES方案的公钥pk←(pks,sp)和私钥sk←sks.

2) 签名生成算法Sig(sk,M,CEAS).为每一个子数据均匀随机地分配一个随机数r[i]，计算每个子数据的承诺值c[i]←C(M[i];r[i])，计算所有承诺值串联的签名σc←Sig(sks,CEAS,〈c[i]〉i∈[n]).最后输出CES方案的签名σF←(CEAS,σc,〈r[i]〉i∈[n]).

3) 截取签名算法Ext(pk,M,σF,X).X为将被移除的子数据的序号集合，同1.1节定义的MOD功能相同.首先为序号为i∈X的子数据计算承诺值c[i]←C(M[i];r[i]).最后，输出CES方案的截取签名σE←(CEAS,σc,〈r[i]〉i∈[n]-X,〈c[i]〉i∈X).

4) 签名验证算法Verify(pk,M′,σE).CI(M′)表示数据M′中包含的所有子数据序号的集合.为序号为i∈CI(M′)的子数据计算承诺值c[i]←C(M′[i];r[i])，运行标准数字签名的验证算法d←Ver(pks,CEAS,〈c[i]〉i∈[n],σc)，d∈{1,0}.d=1表明CES方案的截取签名σE是有效的，否则是无效的.

基于向量承诺的CES方案[13]具有不可伪造性和隐私性.其不可伪造性由标准数字签名的EUF-CMA和消息承诺方案的绑定性(binding)共同保证，隐私性由消息承诺方案的隐藏性(hiding)保证.文献[13]形式化证明了这2个安全性.该方案原始签名生成需要执行一次签名运算和n次承诺运算.与简单的多次签名方案相比，基于向量承诺的CES方案[13]的计算代价小.但是因为原始签名和截取签名中包含所有被保留子数据的承诺随机数和被删除子数据的承诺值，使得签名的长度较长，通信开销较大.

2.2基于MerkleHash树的RSS[12]

Johnson等人[12]于2002年正式定义了具有同态性质的数字签名，并结合Merkle Hash树和伪随机数生成器设计了具体的可修订签名方案.基于Merkle Hash树的RSS[12]主要由7个算法构成：

2) 节点秘密值生成算法：首先选择k比特长的随机数kε作为二叉树T根节点ε的秘密值．如图1所示：二叉树T中父节点秘密值kε作为双倍长伪随机数生成器G的输入，得到左右孩子节点的秘密值〈k0,k1〉←G(kε)，继续计算得到〈k00,k01〉←G(k0)和〈k10,k11〉←G(k1).

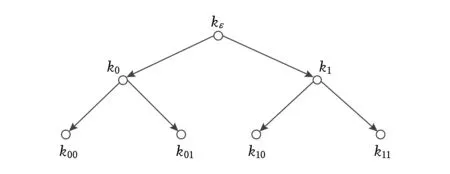
Fig. 1 The generation of nodes’ key value图1 节点秘密值生成

3) 节点Hash值生成算法.叶子节点Hash值vl=H(0,kl,m[l])，父节点Hash值vη=H(1,vη 0,vη 1)，最后计算根节点Hash值vε=H(1,v0,v1).如图2所示:

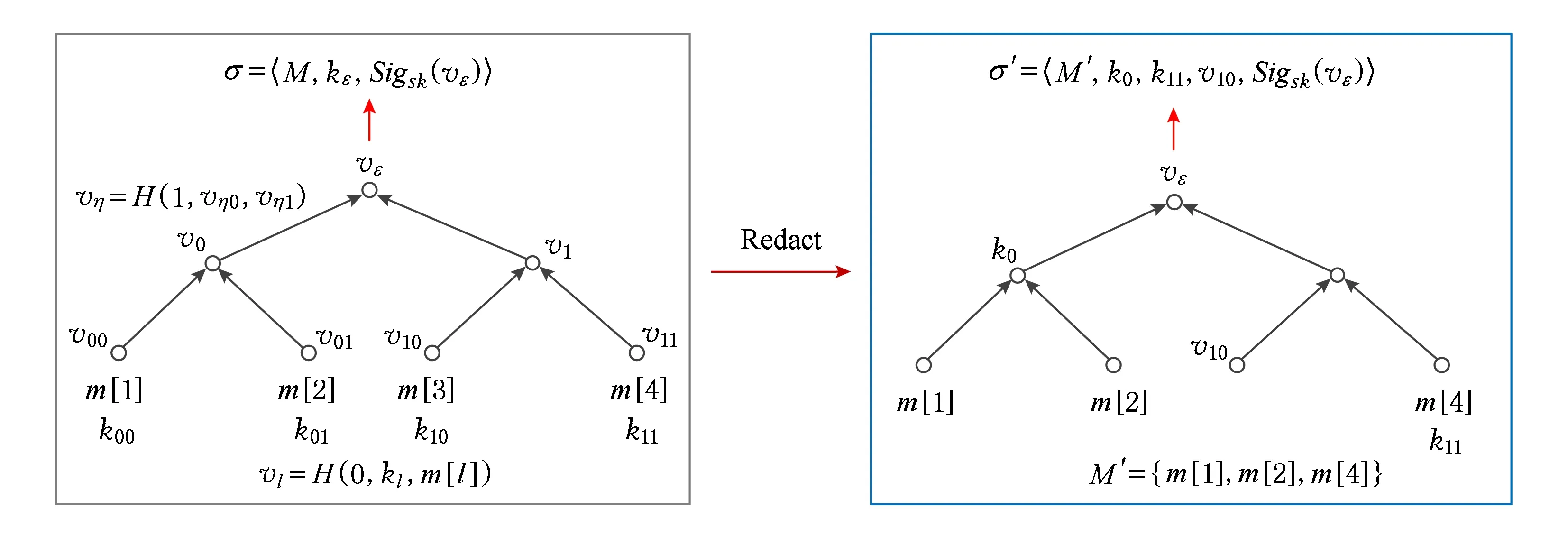
Fig. 2 The generation of redaction signature of RSS based on Merkle Hash Tree图2 基于Merkle Hash树的RSS修订签名生成过程

4) 密钥生成算法.调用标准数字签名的密钥生成算法，输入系统安全参数λ，输出签名人的公私钥对(sk,pk).

5) 签名生成算法.调用标准数字签名的签名算法，计算签名σε←Sig(sk,vε).输出签名结果σ←M,kε,σε.

6) 修订签名生成算法.以数据M={m[1],m[2],m[3],m[4]}为例，如图2.修订者收到签名σ←M,kε,σε.设定MOD={m[3]}，即删除子数据m[3].利用根节点上的秘密值kε，调用节点秘密值生成算法计算出每个叶子节点上的秘密值.调用节点Hash值生成算法计算出每个节点上的Hash值.公开叶子节点m[3]上的Hash值v10，以及从叶子节点m[3]到根节点路径上所有节点的兄弟节点上的秘密值k11,k0.输出修订签名结果σ′←M′,k0,k11,v10,σε，其中M′={m[1],m[2],m[4]}.

7) 验证签名算法.验证者收到签名σ′←M′,k0,k11,v10,σε.利用秘密值k11,k0，调用节点秘密值生成算法计算出每个叶子节点上的秘密值.然后调用节点Hash值生成算法计算出每个节点上的Hash值，得到根节点上的Hash值.调用标准数字签名的验证算法验证d←Ver(pk,,).d=1表明签名是有效的，否则是无效的.

基于Merkle Hash树的RSS[12]具有不可伪造性和隐私性.其不可伪造性由标准数字签名的EUF-CMA和伪随机数生成器的安全性保证，隐私性由Hash函数的强抗碰撞性保证.文献[12]形式化证明了所提出的基于Merkle Hash树的RSS满足不可伪造性要求.该方案的计算代价小且签名长度短，通信开销小.

2.3基于双线性映射的RSS[18]

基于双线性映射的RSS[18]由4个算法构成：

1) 密钥生成算法.均匀随机地选择随机数x←Rp，计算该算法输出签名人的公钥v，私钥x.

3) 修订签名生成算法.修订者可为修订控制条件为DASA的子数据重新分配修订控制条件，具体如下：如果修订者认为某个子数据必须被保留，则将Ci=DASA变为Ci=DASP，同时删除σi；如果修订者想净化某个子数据，则直接删除mi,σi,Ci，再计算σ′←σσi.最后输出修订签名结果←(DID,〈mi,σi,Ci〉i∈[n′],σ′)，其中n′为修订后剩余子数据的数目.

基于双线性映射的RSS[18]具有不可伪造性、隐私性和透明性.其不可伪造性由计算co-Diffie-Hellmann的困难性保证，隐私性由聚合签名的安全性和Hash函数的强抗碰撞性保证.因为该方案原始签名和净化签名组成结构相同，且净化签名不包含被移除子数据的任何信息，第三方无法判断收到的签名是原始签名还是净化签名，因此该方案具有透明性.文献[18]形式化证明了这3个安全性.该方案的签名长度短，但双线性对运算使其计算开销较大.

2.4基于聚合器的RSS[15]

聚合器(accumulator)可为集合型数据生成累加值，并为每个集合成员生成成员证据[47-48].基于聚合器的RSS[15]由4个算法构成：

1) 密钥生成算法：调用传统数字签名算法，输入系统安全参数λ，得到传统数字签名算法的公私钥对(skDSS,pkDSS)；调用聚合器的密钥生成算法，输入系统安全参数λ，得到聚合器算法的公私钥对(skacc,pkacc).最后输出RSS签名人私钥sk←(skDSS,skacc,pkacc)和公钥pk←(pkDSS,pkacc).

2) 签名生成算法.计算集合型数据M的累加值(accM,aux)←AEval((skacc,pkacc),M)，其中accM为数据M的累加值，aux为辅助信息.计算每个子数据mi∈[n]的成员证据witmi←AWitCreate(skacc,pkacc,accM,aux,mi).调用传统数字签名的签名算法计算数据M累加值的签名σDSS←Sig(skDSS,accM).输出签名结果σ←{σDSS,accM,witmi∈[n],ADM}.

3) 修订签名生成算法.输入修订指令MOD，修订后的数据为M′←MMOD，设置WIT′←WIT{witmi}mi∈MOD，即删除被移除子数据的成员证据.输出修订签名结果σ′←{σDSS,accM,WIT′,ADM}.

基于聚合器的RSS[15]具有不可伪造性、隐私性和透明性.其不可伪造性由聚合器的抗碰撞性和标准数字签名的EUF-CMA保证.因为修订后的签名不包含被移除子数据的信息，攻击者很难从修订后的签名得到与被删除子数据有关的任何信息，因此该方案具有隐私性.因为原始签名和修订后签名的组成结构相同，攻击者很难判断收到的签名是原始签名还是修订后签名，所以该方案具有透明性.该方案签名生成的计算代价小，但是由于签名结果中包含每个子数据的成员证据，导致签名长度较长.

3 值得进一步研究的问题

3.1细粒度可控的可修订数字签名

虽然近年来许多国内外的学者从多个方面对可修订数字签名进行了研究，但目前未见支持细粒度修订规则的可修订数字签名的有效设计.在医疗数据提取、数据公开发布等很多应用中，签名持有人并不完全可信.如果不对提取规则进行限制，任由签名持有人移除元素并提取出相应的有效签名，会导致隐私泄露甚至出现与原意不符的数据和签名.目前仅有少数方案支持对签名持有人提取操作的限制，规定了允许被删除或被保留的元素.但这类方案只支持粗粒度的提取规则，不满足实际应用中对门限(threshold)规则、单调(monotone)规则、非单调(non-monotone)规则等丰富修订规则的要求.结合已有的可修订数字签名方案的设计，定义支持细粒度可控的可修订数字签名的安全模型，并提出具体的方案设计，以满足医疗数据提取、数据公开发布等实际应用对可修订数字签名的要求，这是一个值得深入研究的问题.

3.2抗量子攻击的可修订数字签名

随着量子计算机、量子通信和量子密码技术的飞速发展，人类社会正在加速步入量子时代.量子技术无疑将会对人类未来生活产生巨大影响，甚至会引起颠覆性的社会变革[49].电子计算机超强的并行运算能力使得许多原本在传统计算机环境下计算困难的数学问题，在量子计算机环境下却很容易被解决.经典的数字签名都是以求解数学问题的复杂性和困难性为基础的，例如Elgamal签名算法的安全性是基于求解离散对数的困难性，RSA签名算法的安全性是基于求解大整数分解的困难性.目前还没有文献提出抗量子计算的可修订数字签名方案.已被国际密码学界公认的抗量子计算公钥密码体制有基于Hash函数的Merkle树签名、基于纠错码的公钥密码体制、基于格问题的公钥密码体制以及多变量公钥密码体制[50-52].为了迎接量子计算机的挑战，结合已有的可修订数字签名技术和抗量子聚合器、抗量子签名方案[53-54]，设计出适用于量子时代的抗量子计算的可修订数字签名具有重大的现实意义.

3.3安全高效的可修订数字签名

现有的可修订数字签名方案大都不够高效，不是计算代价较大就是存储/通信开销较大.在医疗数据存储/提取、数据公开发布等很多应用中涉及到移动终端.移动终端存储能力和计算能力受限的特点使得现有的可修订数字签名技术在实际应用中受到限制.在保证方案安全性的前提下，设计计算代价小且存储/通信开销小的可修订数字签名是其成功应用的关键.如何结合现代密码学技术和已有的可修订数字签名技术设计出更加安全高效的可修订数字签名仍需做进一步的研究.

4 总 结

本文综述了可修订数字签名的研究现状，描述了其核心算法定义和安全模型，并介绍了现有的具有代表性的可修订数字签名方案，最后探讨了该研究领域中值得进一步研究的问题.

[1] Brown B, Chui M, Manyika J. Are you ready for the era of “big data”[J]. McKinsey Quarterly, 2011, 4(1): 24-35

[2] Diffie W, Hellman M. New directions in cryptography[J]. IEEE Trans on Information Theory, 1976, 22(6): 644-654

[3] Zhang Futai, Sun Yinxia, Zhang Lei, et al. Research on certificateless public key cryptography[J]. Journal of Software, 2011, 22(6): 1316-1332 (in Chinese)

(张福泰, 孙银霞, 张磊, 等. 无证书公钥密码体制研究[J]. 软件学报, 2011, 22(6): 1316-1332)

[4] Katz J, Lindell Y. Introduction to Modern Cryptography[M]. New York: CRC Press, 2014: 193-203

[5] Goldwasser S, Micali S, Rivest R L. A digital signature scheme secure against adaptive chosen-message attacks[J]. SIAM Journal on Computing, 1988, 17(2): 281-308

[6] Tang P C, Ash J S, Bates D W, et al. Personal health records: Definitions, benefits, and strategies for overcoming barriers to adoption[J]. Journal of the American Medical Informatics Association, 2006, 13(2): 121-126

[7] Gostin L O, Lazzarini Z, Neslund V S, et al. The public health information infrastructure: A national review of the law on health information privacy[J]. Journal of the American Medical Association, 1996, 275(24): 1921-1927

[8] Miyazaki K, Susaki S, Iwamura M, et al. Digital documents sanitizing problem[J]. Institute of Electronics, Information and Communication Engineers Technical Reports, 2003 [2017-09-01]. http://ci.nii.ac.jp/naid/10026847332/

[9] Rivest R L. Two signature schemes[OL]. [2015-09-14]. http://people.csail.mit.edu/rivest/pubs.html

[10] Traverso G, Demirel D, Buchmann J. Homomorphic Signature Schemes: A Survey[M]. Berlin: Springer, 2016: 53-58

[11] Pöhls H C, Peters S, Samelin K, et al. Malleable signatures for resource constrained platforms[C] //Proc of IFIP Int Workshop on Information Security Theory and Practices. Berlin: Springer, 2013: 18-33

[12] Johnson R, Molnar D, Song D, et al. Homomorphic signature schemes[C] //Proc of 2002 Cryptographers Track at the RSA Conf. Berlin: Springer, 2002: 244-262

[13] Steinfeld R, Bull L, Zheng Yuliang. Content extraction signatures[C] //Proc of the 4th Int Conf on Information Security and Cryptology. Berlin: Springer, 2001: 285-304

[14] Pöhls H C, Samelin K, Posegga J, et al. Length-hiding redactable signatures from one-way accumulators inO(n), MIP-1201[R]. Passau: Faculty of Computer Science and Mathematics, University of Passau, 2012

[15] Derler D, Pöhls H C, Samelin K, et al. A general framework for redactable signatures and new constructions[C] //Proc of the 18th Int Conf on Information Security and Cryptology. Berlin: Springer, 2015: 3-19

[16] Nojima R, Tamura J, Kadobayashi Y, et al. A storage efficient redactable signature in the standard model[G] //LNCS 5735: Proc of the 12th Int Conf on Information Security. Berlin: Springer, 2009: 326-337

[17] Miyazaki K, Iwamura M, Matsumoto T, et al. Digitally signed document sanitizing scheme with disclosure condition control[J]. IEICE Trans on Fundamentals of Electronics, Communications and Computer Sciences, 2005, 88(1): 239-246

[18] Miyazaki K, Hanaoka G, Imai H. Digitally signed document sanitizing scheme based on bilinear maps[C] //Proc of the 2006 ACM Symp on Information, Computer and Communications security. New York: ACM, 2006: 343-354

[19] Pöhls H C, Samelin K. On updatable redactable signatures[C] //Proc of the 12th Int Conf on Applied Cryptography and Network Security. Berlin: Springer, 2014: 457-475

[20] Attrapadung N, Libert B, Peters T. Efficient completely context-hiding quotable and linearly homomorphic signatures[C] //Proc of Public Key Cryptography. Berlin: Springer, 2013: 386-404

[21] Bauer D, Blough D M. Analysis of a redactable signature scheme on data with dependencies[R]. Atlanta: Georgia Institute of Technology, 2009

[22] Pöhls H C, Samelin K. Accountable redactable signatures[C] //Proc of the 10th Int Conf on Availability, Reliability and Security (ARES). Piscataway, NJ: IEEE, 2015: 60-69

[23] Haber S, Hatano Y, Honda Y, et al. Efficient signature schemes supporting redaction, pseudonymization, and data deidentification[C] //Proc of the 2008 ACM Symp on Information, Computer and Communications Security. New York: ACM, 2008: 353-362

[24] Lim S, Lee E, Park C M. A short redactable signature scheme using pairing[J]. Security and Communication Networks, 2012, 5(5): 523-534

[25] Attrapadung N, Libert B, Peters T. Computing on authenticated data: New privacy definitions and constructions[C] //Proc of the 18th Int Conf on the Theory and Application of Cryptology and Information Security. Berlin: Springer, 2012: 367-385

[26] Kundu A, Bertino E. Structural signatures for tree data structures[J]. Proceedings of the VLDB Endowment, 2008, 1(1): 138-150

[27] Chang Chien, Lim C L, Xu Jia. Short redactable signatures using random trees[C] //Proc of the 2009 Cryptographers’ Track at the RSA Conf. Berlin: Springer, 2009, 9: 133-147

[28] Brzuska C, Busch H, Dagdelen O, et al. Redactable signatures for tree-structured data: Definitions and constructions[C] //Proc of the 8th Int Conf on Applied Cryptography and Network Security. Berlin: Springer, 2010: 87-104

[29] Slamanig D, Rass S. Generalizations and extensions of redactable signatures with applications to electronic healthcare[C] //Proc of the 11th Int Conf on Communications and Multimedia Security. Berlin: Springer, 2010: 201-213

[30] Lim S, Lee H S. A short and efficient redactable signature based on RSA[J]. ETRI Journal, 2011, 33(4): 621-628

[31] Samelin K, Pöhls H C, Bilzhause A, et al. On structural signatures for tree data structures[G] //LNCS 7341: Proc of ACNS 2012. Berlin: Springer, 2012: 171-187

[32] Samelin K, Pöhls H C, Bilzhause A, et al. Redactable signatures for independent removal of structure and content[C] //Proc of the 8th Int Conf on Information Security Practice and Experience. Berlin: Springer, 2012: 17-33

[33] Hirose S, Kuwakado H. Redactable signature scheme for tree-structured data based on Merkle tree[C] //Proc of 2013 Int Conf on Security and Cryptography (SECRYPT). Piscataway, NJ: IEEE, 2013: 1-8

[34] de Meer H, Pöhls H C, Posegga J, et al. Redactable signature schemes for trees with signer-controlled non-leaf-redactions[C] //Proc of 2012 Int Conf on E-Business and Telecommunications. Berlin: Springer, 2012: 155-171

[35] Wei Baodian. Applications of trees in special signatures[J]. Computer Engineering and Applications, 2006, 42(11): 16-20 (in Chinese)

(韦宝典. 树结构在几种特殊签名中的应用研究[J]. 计算机工程与应用, 2006, 42(11): 16-20)

[36] Bull L, Squire D M G, Zheng Yuliang. A hierarchical extraction policy for content extraction signatures[J]. International Journal on Digital Libraries, 2004, 4(3): 208-222

[37] Bauer D, Blough D M, Mohan A. Redactable signatures on data with dependencies and their application to personal health records[C] //Proc of the 8th ACM Workshop on Privacy in the Electronic Society. New York: ACM, 2009: 91-100

[38] Wu Zhenyu, Hsueh C W, Tsai C Y, et al. Redactable signatures for signed CDA documents[J]. Journal of Medical Systems, 2012, 36(3): 1795-1808

[39] Brown J, Blough D M. Verifiable and redactable medical documents[C] //Proc of 2012 AMIA Annual Symp. San Francisco: American Medical Informatics Association, 2012: 11-48

[40] Kundu A, Bertino E. Privacy-preserving authentication of trees and graphs[J]. International Journal of Information Security, 2013, 12(6): 467-494

[41] Pöhls H C, Karwe M. Redactable signatures to control the maximum noise for differential privacy in the smart grid[C] //Proc of the 2nd Int Workshop on Smart Grid Security. Berlin: Springer, 2014: 79-93

[42] Bull L, Squire D M G, Newmarch J, et al. Grouping verifiable content for selective disclosure[C] //Proc of Australasian Conf on Information Security and Privacy. Berlin: Springer, 2003: 1-12

[43] Camenisch J, Dubovitskaya M, Haralambiev K, et al. Composable and modular anonymous credentials: Definitions and practical constructions[C] //Proc of the 21st Int Conf on the Theory and Application of Cryptology and Information Security. Berlin: Springer, 2014: 262-288

[44] Brzuska C, Pöhls H C, Samelin K. Efficient and perfectly unlinkable sanitizable signatures without group signatures[C] //Proc of the 10th European Public Key Infrastructure Workshop. Berlin: Springer, 2013: 12-30

[45] Brzuska C, Pöhls H C, Samelin K. Non-interactive public accountability for sanitizable signatures[C] //Proc of the 10th European Public Key Infrastructure Workshop. Berlin: Springer, 2012: 178-193

[46] Ma Jinhua, Liu Jianghua, Wang Min, et al. An efficient and secure design of redactable signature scheme with redaction condition control[C] //Proc of the 12th Int Conf on Green, Pervasive, and Cloud Computing. Berlin: Springer, 2017: 38-52

[47] Derler D, Hanser C, Slamanig D. Revisiting cryptographic accumulators, additional properties and relations to other primitives[C] //Proc of the 2015 Cryptographer’s Track at the RSA Conf. Berlin: Springer, 2015: 127-144

[48] Benaloh J, De Mare M. One-way accumulators: A decentralized alternative to digital signatures[C] //Proc of 1993 Workshop on the Theory and Application of of Cryptographic Techniques. Berlin: Springer, 1993: 274-285

[49] Guo Hong, Li Zhengyu, Hu Bian. Quantum Cryptography[M]. Beijing: National Defence Industry Press, 2016 (in Chinese)

(郭弘, 李政宇, 彭编. 量子密码[M]. 北京: 国防工业出版社, 2016)

[50] Regev O. Lattice-based cryptography[C] //Proc of the 26th Annual Inte Cryptology Conf. Berlin: Springer, 2006: 131-141

[51] Zeng Guihua. Quantum Cryptography[M]. Beijing: Science Press, 2006 (in Chinese)

(曾贵华. 量子密码学[M]. 北京: 科学出版社, 2006)

[52] Libert B, Mouhartem F, Nguyen K. A lattice-based group signature scheme with message-dependent opening[C] //Proc of the 14th Int Conf on Applied Cryptography and Network Security. Berlin: Springer, 2016: 137-155

[53] Zhang Jiang, Chen Yu, Zhang Zhenfeng. Programmable Hash functions from lattices: Short signatures and IBEs with small key sizes[C] //Proc of the 36th Annual Cryptology Conf. Berlin: Springer, 2016: 303-332

[54] Libert B, Ling San, Nguyen K, et al. Zero-knowledge arguments for lattice-based accumulators: logarithmic-size ring signatures and group signatures without trapdoors[C] //Proc of the 35th Annual Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2016: 1-31

SurveyonRedactableSignatures

Ma Jinhua1,2, Liu Jianghua3, Wu Wei1,2, and Huang Xinyi1,2

1(SchoolofMathematicsandInformation,FujianNormalUniversity,Fuzhou350007)2(FujianProvincialKeyLaboratoryofNetworkSecurityandCryptology(FujianNormalUniversity),Fuzhou350007)3(SchoolofInformationTechnology,DeakinUniversity,Melbourne,Australia3125)

Data security issues have become a serious challenge to national economic, political, defence and cultural security. As a core technology in protecting data security, digital signatures have been widely used for the verification of data integrity and source authenticity. The security definition of conventional digital signatures is existentially unforgeable against adaptive chosen-message attacks. Although it meets the basic security requirement of data authentication, it hampers the reasonable operation of authenticated data which is desirable in many practical applications. As a type of malleable homomorphic signatures for editing, redactable signatures allow the signature holder (redactor) to delete sensitive portions of the signed data and generate a valid signature for the disclosed data without any help from the original signer. It has been a research hotspot in the field of cryptography since it was introduced in 2001. In recent years, many researchers have studied redactable signatures from the aspects of formal security definition, redaction control mechanism, computational cost and communication overhead, and there are lots of research results. However, the rapid development of network technology and its applications are putting forward new challenges to redactable signatures. This paper summarizes and analyses redactable signatures in terms of algorithm definition, security model and representative designs. Furthermore, some existing problems worthy of further study are also discussed.

redactable signatures; homomorphic signatures; digital signature; data authentication; security model

TP309

MaJinhua, born in 1990. PhD. Her main research interests include cryptography and information security.

LiuJianghua, born in 1988. PhD. His main research interests include cryptography and information security.

WuWei, born in 1981. PhD, associate professor. Her main research interests include cryptography and information security.

HuangXinyi, born in 1981. PhD, professor, PhD supervisor. His main research interests include cryptography and information security.