隐私保护集合交集计算技术研究综述

申立艳 陈小军 时金桥 胡兰兰

1(中国科学院大学网络空间安全学院 北京 100049) 2(中国科学院信息工程研究所 北京 100093) (shenliyan@iie．ac．cn)

2017-06-11；

2017-07-28

国家自然科学基金项目(61602474) This work was supported by the National Natural Science Foundation of China (61602474).

陈小军(chenxiaojun@iie.ac.cn)

隐私保护集合交集计算技术研究综述

申立艳1,2陈小军2时金桥2胡兰兰2

1(中国科学院大学网络空间安全学院 北京 100049)2(中国科学院信息工程研究所 北京 100093) (shenliyan@iie．ac．cn)

隐私保护集合交集(private set intersection, PSI)计算属于安全多方计算领域的特定应用问题，不仅具有重要的理论意义也具有很强的应用背景，在大数据时代，对该问题的研究更是符合人们日益强烈的在享受各种服务的同时达到隐私保护的需求.对安全多方计算基础理论进行了简要介绍，并重点介绍了目前主流的安全多方计算框架下2类PSI研究技术：传统的基于公钥加密机制，混乱电路，不经意传输的PSI协议和新型的云辅助的PSI协议，并对各类协议的过程、适用性、复杂性进行简要分析总结.同时，也对隐私保护集合交集问题的应用场景进行详细说明，进一步体现对该问题的实际研究价值.随着对该问题的不断深入研究，目前已经设计了在半诚实模型下快速完成上亿元素规模的隐私集合求交集协议.

隐私保护集合交集；安全多方计算；不经意传输；混乱电路；不经意伪随机函数计算；不经意多项式计算；云计算

随着通信技术、网络技术等的快速发展以及移动计算、云计算、分布式计算等广泛应用，虚拟网络和人们的生活联系更加紧密，互联网大数据的各种应用渗透到人们的社交、购物、出行等方方面面.这些应用让人们享受到更加便捷的服务，但同时大量有价值的客户信息、个人的隐私记录、企业运营数据不断被挖掘，人们的隐私受到越来越强烈的威胁.因此，大数据时代的隐私保护问题成为学术界及工业界关注的焦点.

从数据生命周期角度来看，数据经历了数据发布、数据存储、计算挖掘和数据使用等环节，据此研究者提出了大数据发布隐私保护技术、大数据存储隐私保护技术、大数据计算和挖掘隐私保护技术以及大数据访问控制技术等来从各个环节保护数据的隐私[1].而在这些大数据隐私保护技术里，更基本的技术是隐私保护的数据计算，指能够满足人们在不泄露额外信息的同时，完成隐私数据之间的计算任务，比如相似性计算[2-3]、距离计算[4-6]等任务.本文主要关注其中的一类即隐私保护集合交集计算技术.

常用的大数据隐私保护技术手段包括匿名、失真、加密、安全多方计算等的方法[1].安全多方计算作为一种特殊的分布式环境下的隐私保护计算方法在近年来受到研究者的普遍关注，已经成为密码学领域的重要研究方向.安全多方计算是由图灵奖获得者姚期智在1982年提出[7]，主要解决在分布式计算场景下互不信任的数据拥有者安全协同计算问题，既实现了资源共享又保证了数据隐私性需求.安全多方计算包含的内容十分丰富，包括基础理论模型研究[8-10]、基础密码协议研究、特定应用协议等的研究.基础密码协议包含混乱电路(garbled circuit， GC)、不经意传输(oblivious transfer, OT)、秘密共享(secret sharing, SS)、同态加密(homomorphic encryp-tion, HE)、零知识证明(zero knowledge proof)、掷币协议(coin tossing)、比特承诺(bit commitment)协议等，这些密码协议都可以看作特殊的安全多方计算问题，由一组存在各种信任关系的参与者通过交互或非交互操作来完成某一功能函数的安全计算；特定应用协议研究包括隐私集合运算[11-12]、隐私保护数据挖掘[13-16]、隐私保护信息检索[17-19]、几何计算[20-21]等.基础密码协议成为应用协议设计的基本工具，其安全性和效率直接影响调用它们的应用协议的安全性和效率.

隐私保护集合交集(private set intersection, PSI)计算是安全多方计算领域的一个重要方面，不仅在科学计算中有很好的体现，在现实生活中很多数据都可以用集合来表示，并用集合间的隐私保护计算来完成一些数据计算问题，因此PSI计算有很广泛的应用场景.对该问题的具体定义是在不泄露各自参与方输入信息的前提下，协同计算输入集合的交集.典型的应用场景有隐私保护相似文档检测、私有联系人发现、安全的人类基因检测[22]、隐私保护的近邻检测[23]、隐私保护的社交网络关系发现[24]、在线推荐服务和婚恋网站配对等.在数据由不同管理者持有的条件下，PSI计算达到一种保护隐私与信息共享的共赢.

PSI计算研究由Freedman等人在2004年提出[25]，借助不经意多项式求值和同态加密实现.这种实现受限于基础密码协议的计算代价，传统的应用系统还是采用不安全Hash协议*https://www.eff.org/deeplinks/2012/09/deep-dive-facebook-and-datalogix-whats-actually-getting-shared-and-how-you-can-opt实现PSI，即对参与方的集合分别进行Hash映射，在Hash值基础上求集合交集.显而易见，这种方法很容易受到碰撞攻击.随着近年来对PSI问题的深入研究，在NDSS，USENIX，CCS等著名国际信息安全会议上涌现了大量的相关研究成果.对该问题的研究不仅推动安全多方计算基础理论的研究发展，也推动了PSI计算实际应用问题研究的发展.目前某些PSI协议的性能已经得到了很大的提高，在通信和计算复杂度上达到了与不安全的Hash协议同样的量级[26].

PSI计算技术根据是否有第三方参与主要分为两大类：1)传统的PSI计算技术，参与方直接交互执行真实的协议，达到隐私计算集合交集的目的，这类技术根据实现原理又包含基于公钥加密机制、混乱电路和不经意传输等3类PSI协议；2)云辅助的PSI计算技术，也叫外包的隐私保护集合交集计算(outsourced private set intersection, OPSI)，主要利用云服务器的强大计算资源，完成安全交集计算.与理想协议中的可信第三方一样，云服务器主要承担计算交集的作用，但没有任何输入输出信息.表1为2类方法异同点对比.

Table 1 The Comparison of Two Research Methods for PSI表1 PSI两类研究方法对比

本文拟对PSI技术的研究现状进行全面的梳理，针对传统的PSI计算技术和云辅助的PSI技术的具体研究思路、研究方法、适用的安全假设、敌手模型和性能开销进行详细介绍和对比，并对基于PSI计算技术的应用研究做了简要的整理，对当前PSI计算技术存在的问题和研究趋势进行总结和建议.

1 基础原语

1.1安全性证明方法

任何提出的安全协议都需要进行安全性证明，一般来说，在安全多方计算中提出的安全协议通过与理想模型进行对比来证明其安全性.所谓理想模型是指存在可信的第三方，其计算能力是概率多项式时间，通过安全信道获得各参与方的隐私输入并计算功能函数f，将结果秘密发送给协议参与方.对于所提出的安全协议在证明其安全性时，需要对比理想模型来说明每一个参与方都不会获得更多的信息，这种安全性证明方法叫理想-现实模拟方法[27]；如果放宽安全性要求，只需某一参与方遵循安全要求的话，称为单边模拟方法.

1.2安全模型

在协议的安全性证明过程中，有2类非常重要的基础模型，分别是标准模型和随机预言模型.标准模型(standard model， Std)指不依赖任何假想模型，仅依赖于被广泛接受的困难性假设(如因子分解、离散对数等)，这些数学难题是攻击者在多项式时间内不可解的.仅使用困难性假设证明安全的机制称为在标准模型下是安全的.随机预言模型(random oracle model， ROM)[28]比标准模型多了一个随机预言机的假设，随机预言机假设存在一个公共的、随机选择的函数(理论上的黑盒子)，只能通过问询的方式进行计算，对每一次查询都从输出域中均匀随机地输出一个响应，对相同的查询总是得到相同的响应.由于现实中没有函数能够实现真正的随机函数，因此随机预言模型下可证明安全的方案在实际应用中通常用Hash函数进行实例化.

1.3敌手模型

根据敌手腐败参与方的行为方式，敌手模型一般分为3类[27]：

1) 半诚实模型(honest but curious adversary, HbC).协议的各参与方遵守协议的执行过程，但可以在协议执行过程中，根据输入和协议的输出信息推断其他参与者的信息.

2) 恶意模型(malicious adversary, Mal).参与者不遵守协议的执行过程，可能拒绝参与协议、修改隐私的输入集合信息、提前终止协议的执行等，因此需要使用更多的密码协议或技术(位比特承诺协议、零知识证明等)来保证计算结果的正确性.

3) 隐蔽敌手模型(covert adversary).是一种安全性介于半诚实模型和恶意模型之间的更符合真实场景的模型，由于担心恶意行为被协议检测出来并受到惩罚，隐蔽敌手使其恶意行为混淆在正常行为中，只能以一定的概率被检测到.

1.4基础协议

不经意传输协议(OT)是基于公钥密码体制的密码学基本协议，是安全多方计算的基石.最基本的二选一OT协议的发送方Bob输入2个随机位串(x0,x1)，接收方Alice输入选择向量c；协议结束后Alice获得选择向量对应的位串xc，对另一个位串x1-c一无所知；Bob的输出为空[29].在1988年Impagliazzo 和 Rudich 证明了从不经意传输协议到单向函数的黑盒式规约蕴含着另一个难以被证明的问题，即P≠NP的问题，并表示不存在黑盒方式的OT协议[30]，因此OT协议通常是基于公钥密码体制来构造.然而在安全多方计算应用中一般需要大量的OT协议作为子协议，计算复杂的模指数运算，使得OT协议的实用价值不高.1996年Beaver依据混合加密构想提出了第1个非黑盒方式的不经意传输扩展协议[31]，可以执行少数基础OT协议(传统的基于公钥加密算法的OT协议)来构造大量的OT协议，然而Beaver提出的协议需要计算复杂的伪随机发生器，在实际中也不高效，但是扩展协议的思想具有重要的影响.基于OT扩展协议的思想Ishai等人在2003年提出了以黑盒方式构造的OT扩展协议[32]，将基础OT协议和随机预言模型相结合，把少量基础OT的计算代价通过对称加密操作均摊到大量的OT操作，可以达到1 min执行数百万次的OT协议，该协议可以同时满足实用性和安全性需求，具有重要的意义并得到很广泛的应用，例如GMW协议、姚氏混乱电路、PSI等.随着人们对实用性要求越来越高，OT扩展协议得到了快速发展，主要包括对N选1不经意传输扩展协议[33]及随机OT[34]协议的提出.

混乱电路(GC)模型最早是由图灵奖获得者姚期智在1986年提出的半诚实模型下的姚氏电路[35]，用来解决著名的百万富翁问题.姚氏电路主要是将任意功能函数转化为布尔电路，由Alice生成混乱电路表、Bob计算混乱电路；针对每一个电路门进行两重对称加解密运算，调用四选一OT协议进行混乱电路表中秘钥信息交换.早期的安全函数计算问题主要采用混乱电路来解决，由于混乱电路对每一位进行电路门计算并且电路门数量巨大，导致计算效率较低，例如计算AES加密大约需要30 000个电路门，计算50个字符串的编辑距离大约需要250 000个电路门[36].混乱电路作为通用的安全多方计算工具，可以用来计算任意的功能函数,相对于特定问题的安全协议计算效率较低.针对这些问题，研究者提出了一系列的电路优化策略[37]，包括Free-XOR、行约减[38-39]、Half-Gate技术[40].此外还提出了新的混乱电路协议，包括由Goldreich等人提出基于秘密共享和OT协议的GMW编译器[8]以及基于剪切-选择技术(cut and choose)[41]的适用于恶意模型的混乱电路等.除了对布尔电路的研究人们也提出了算术电路，完成有限域上加法或乘法运算.混乱电路方法作为安全多方计算问题的一般通用解决方法，近年来得到了快速的发展，已经有很多实用的安全多方计算工具，例如Fairplay[42],FastGC[43],Oblivm[44],SEPIA[45],VIFF[46],Sharemind[47]等.

同态加密(HE)是满足同态性质的公钥加密技术，属于语义安全的公钥加密体制范畴.同态加密对密文进行某种算术操作(加或者乘)，满足对密文计算结果的解密值与对明文进行同样算术操作的值是相同的性质.由于计算是在密文上进行，因此同态加密是一种常用的实现隐私保护的方法.

秘密共享(SS)将秘密以适当的方式分为n份，每一份由不同的管理者持有，每个参与者无法单独恢复秘密，只有达到指定数目的参与者才能恢复秘密.构建秘密共享系统的关键是设计好的秘密拆分和恢复方式.第1个秘密共享方案是(t,n)门限秘密共享方案，由Shamir[48]和Blakley[49]分别在1979年各自独立提出，他们的方案分别是基于拉格朗日插值法和线性几何投影性质设计的.此后很多研究者提出了不同的秘密共享实现方法，如基于中国剩余定理的秘密共享策略、可验证的秘密共享等.秘密共享在密钥管理分布式数据安全领域有许多应用，如电子投票、 密钥托管、电子支付协议等，可以防止密钥存储过于集中，是一种兼顾机密性和可靠性的方法.

1.5符号说明

为了方便后续的讨论，本文对所有的数学符号含义进行统一约定，如表2所示:

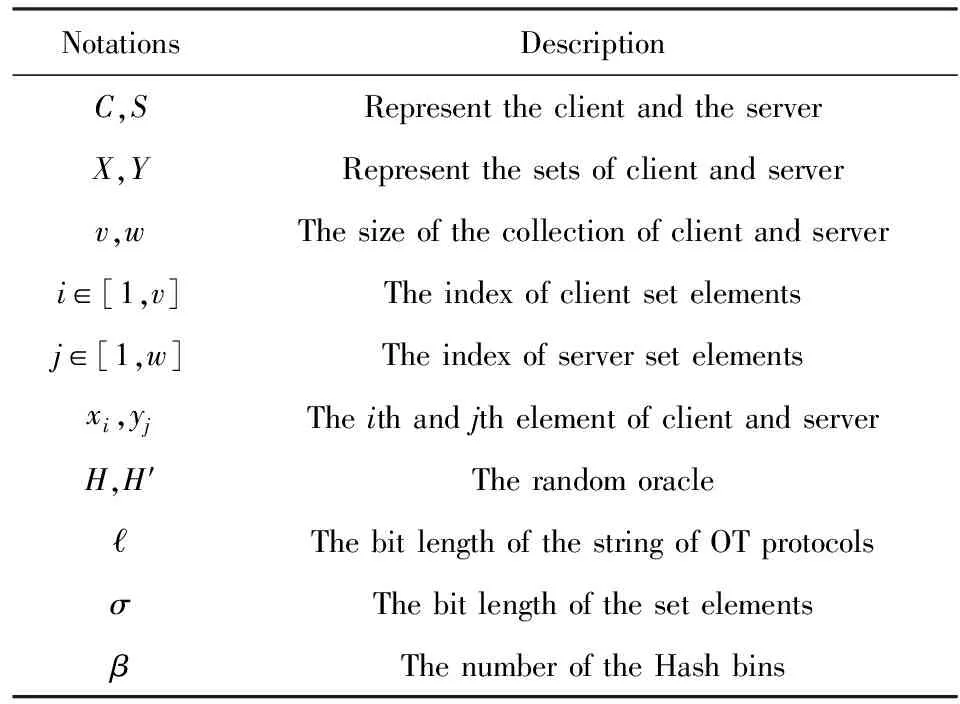
Table 2 The Notation and Description表2 符号说明

2 传统的PSI计算技术

传统的PSI协议主要是参与方之间通过一系列底层的密码学技术直接进行交互计算，根据底层所采用技术的不同主要分为3类协议，分别为基于公钥加密机制的PSI、基于混乱电路的PSI、基于OT协议的PSI.

2.1基于公钥加密体制

基于公钥加密体制的方法主要对集合元素进行复杂的公钥加密操作如同态加密，并在密文上进行计算.根据协议设计思想的不同又分为基于不经意多项式计算(oblivious polynomial evaluation, OPE[50])的PSI、基于不经意伪随机函数(oblivious evaluation of pseudorandom functions, OPRF)的PSI和基于盲签名的PSI.

2.1.1 基于不经意多项式计算的PSI

不经意多项式计算的PSI协议主要是将参与方集合元素表示为多项式的根，利用多项式的数学性质来计算交集，并采用同态加密算法加密交互过程中的信息来保证协议的隐私性.

与文献[25]中的方法不同，2005年Kissner等人提出不经意多项式计算PSI协议的另一种实现[11].该协议依据多项式的数学性质来求集合交集：任意2个集合SA,SB表示为多项式PA,PB，那么gcd(PA,PB)表示集合交集SA∩SB，gcd表示最大公约数.协议的计算过程为：客户端将集合元素表示为v次多项式PA的根,在多项式环R[x]上随机选取v次多项式γA并计算PA.γA,同理服务端将集合元素表示为v次多项式PB的根*为描述简单起见，此处假设客户端和服务器端集合大小相同均为v.，随机选取v次多项式γB计算PB.γB并将计算结果同态加密发送给客户端；此时，客户端可以计算PA.γA+PB.γB=u.gcd(PA,PB) .根据文献[11]中的定理有：由于γA和γB为随机选择的多项式，u为多项式环上均匀分布的任意2v-|SA∩SB|次多项式，其解为集合SA或SB中元素的概率可忽略不计.因此,客户端利用同态加密的性质在密文上完成PSI计算.该协议被证明多个参与者在半诚实敌手模型下是安全的.针对恶意敌手模型,文中采用零知识证明技术防止参与方偏离协议执行.基于同样的思想，Dachman等人提出将多项式进行秘密共享的恶意模型下的PSI协议[56].在2017年，周素芳等人也在将集合表示成多项式的基础上利用秘密共享协议设计了半诚实模型下高效的PSI方案[57].

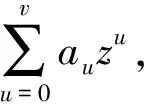
针对恶意敌手模型，文献[25]在其基础上提出对恶意客户端采用cut and choose技术，对恶意服务器端采用随机预言模型，保证协议的安全性.2010年Hazay等人对文献[25]中协议进一步改进，提出了一种适用于标准模型下恶意敌手的协议[59].该协议将文献[25]中的z=Enc(r.P(y)+y)替换为z=Enc(r.P(y)+s)，其中s与y相互独立，s由服务器端随机生成，并将s的比特承诺值发送给客户端，s同时也用来计算伪随机函数[60]r=Fk(s).如果客户端某一元素x不属于集合交集，那么Dec(z)为一随机数，反之客户端会获得s=Dec(z)，客户端通过对比Dec(z)的值和s的比特承诺值确定元素x是否属于集合交集.进一步，客户端通过与服务器端交互可获得伪随机函数值r=Fk(s)，可以用来检验服务器端传输加密数据的正确性.该协议采用比特承诺协议可以有效防止服务端输入数据不一致以及零知识证明协议保证客户端输入多项式不恒为零.

2.1.2 基于不经意伪随机函数的PSI

基于不经意伪随机函数的PSI协议主要思想是客户端和服务器端利用不经意伪随机函数Fk()来计算不经意伪随机函数值集合{Fk(x)}x∈X,{Fk(y)}y∈Y,再完成集合交集计算.其中，在不经意伪随机函数的计算过程中，服务器端拥有计算秘钥k,客户端输入X通过协同计算得到{Fk(x)}x∈X，服务器端在本地计算{Fk(y)}y∈Y并发送给客户端.该过程中客户端不能得到任何有关函数Fk()和秘钥k的信息，服务器端不能得到任何有关X的信息，从而保证信息的隐私性.

与文献[61]不同，2009年Jarecki等人基于复合剩余假设提出了另一种PSI协议[62]，该协议采用Dodis-Yampolskiy伪随机函数[63]的形式:Fk(x)=g,利用Camenisch-Shoup[64]加同态加密和零知识证明技术实现伪随机函数的计算，进一步在伪随机函数值集合上完成交集运算.该协议依赖于公共参考串模型并限制输入集合定义域大小，是恶意模型下可证明安全的PSI协议.

2.1.3 基于盲签名的PSI

基于盲签名PSI协议的主要思想是客户端将集合元素盲化处理，然后让服务器端对盲化的消息进行签名，最后客户端对签字除去盲因子，得到服务器端关于集合元素的签名{Sign(x)}x∈X；服务器端在本地计算集合元素签名{Sign(y)}y∈Y并发送给客户端；客户端在{Sign(x)}x∈X{Sign(y)}y∈Y的基础计算集合交集.基于盲签名函数的设计本身可保证协议信息的隐私性.

2.1.4 公钥加密的PSI性能比较分析

为了对以上各协议性能有更直观的认识，分别从安全模型(标准模型、随机预言模型)、敌手模型(半诚实、恶意敌手)的角度对客户端和服务器端计算和通信复杂度进行渐进分析.分析结果如表3所示：

Table 3 Comparison of Private Set Intersection Protocols表3 隐私集合交集协议性能比较

Note： exps denotes modular exponentiations operation.

几种协议的通信复杂度一般都与集合元素成线性关系，协议主要的操作均为复杂的模指数操作，计算复杂度通常与模指数的长度成线形关系，由于大部分协议采用同态加密及其他公钥算法指数和模数一般为1 024 b以上，而De Cristofaro等人提出的PSI协议模指数计算中的指数为160 b，模数为1 024 b，因此计算复杂度最低.

2.2基于混乱电路

理论上讲，任意的功能函数均可用基本的电路门形式来表示，即可以通过电路解决任意功能函数计算问题，因此可以用混乱电路的方法计算PSI问题.基于混乱电路的PSI协议主要思想有2种:1)将元素映射到二进制向量，通过向量的与运算求集合交集；2)通过电路解决隐私保护的元素相等性判断问题，然后通过集合中元素的两两比较以O(n2)复杂度计算集合交集.

2012年Huang等人提出了3种基于姚氏混乱电路PSI协议的实现[71]，分别为BWA(Bitwise-AND)，PWC(Pairwise-Comparisons)，SCS(Sort-Compare-Shuffle)，分别适用于不同的集合规模和集合定义域大小的计算.其中，BWA协议将集合中σ位长的元素表示成长度为2σ位向量，向量中每一位表示集合中一个元素，位向量中某一位为1表示元素在集合中，为0表示该元素不在集合中.通过混乱电路对参与方集合向量进行位与运算得出交集集合的位向量，进而得到相应元素.PWC协议主要通过混乱电路对两方的元素进行两两相等判断，首先将2个长度为σ位的元素进行XOR运算，并将计算结果的每个位进行OR运算，由于协议采用了Free-XOR技术[72]，每对元素间相等性判断只需要实现σ-1个非异或门电路.SCS协议的主要过程为：客户端和服务器端分别在本地对各自集合中元素进行排序，并通过混乱电路进行按序合并；对合并后集合中相邻元素进行相等性判断，如果相等则为交集中元素；最后将计算结果乱序(分别采用了3种方法实现乱序：不经意排序网络、同态加密、Waksman 网络，乱序目的是防止泄露集合元素位置信息)输出给客户端.该协议通过使用不经意扩展传输协议及其他各种电路优化技术，仅需要O(σnlogn)非异或门电路操作，大大加快了协议的计算速度.这些实现方案均假设参与方集合没有重复元素，在半诚实敌手模型下是可证明安全的.

2014年Pinkas等人对Huang提出的PWC，SCS协议进行优化[73]，主要是采用目前最快的随机OT协议对混乱电路进行优化.由于混乱电路以OT子协议为基础完成安全计算，因此OT协议的改进很大程度减少协议的计算和通信代价.此外Pinkas等人也利用GMW混乱电路进行PSI协议计算，该协议同样采用随机OT协议加快PSI的计算.除了从OT协议的角度对姚氏混乱电路和GMW混乱电路进行优化外，在PWC协议中作者采用Hash函数将集合元素进行映射来减少两两元素相等判断比较次数，很大程度减少协议计算复杂度.

2016年Pinkas等人通过电路实现了基于不经意伪随机函数的PSI[74]，该协议的关键在于如何高效地实例化OPRF，作者采用文献[38]中AES实例化OPRF，并分别用姚氏混乱电路和GMW混乱电路计算AES函数完成PSI计算.

表4对以上基于混乱电路的协议进行渐进复杂度分析，分析结果如下：

Table 4 Comparison of Private Set Intersection Protocols表4 集合交集协议性能比较

Note：n: the size of sets;κ: the symmetric security parameter.

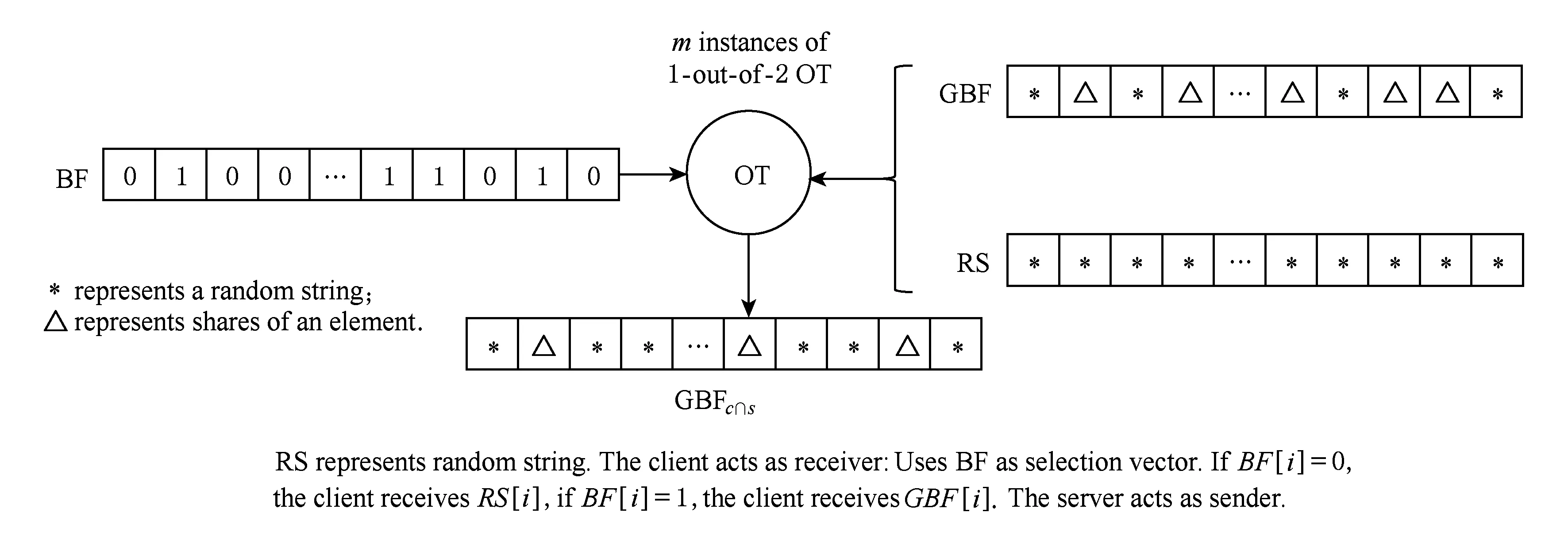
Fig. 1 The private set intersection protocol based on Bloom filter.图1 基于布隆过滤器的隐私集合交集协议

BWA协议计算代价与σ成指数关系，适用于较小的σ值.结合文献[73-74]中实验结果对以上PWC，SCS协议进行分析，由于PWC协议采用Hash函数减少比较次数，无论采用姚氏混乱电路还是GMW混乱电路在计算和通信复杂度上都优于SCS协议.

尽管混乱电路的PSI协议一般具有通用性、灵活性和可扩展性，但功能函数的电路设计一般要求很大的门电路个数和电路深度，因此基于此技术的协议一般计算效率很低，人们更偏向于使用特殊的高效协议.

2.3基于不经意传输协议

基于不经意传输的PSI协议主要是通过OT协议进行向量或元素相等性判断来完成集合交集计算.随着近年来OT协议的快速发展，基于OT协议的应用协议也得到了快速发展.特别是基于OT协议的PSI计算可以快速完成上亿元素规模的交集计算，逐渐可适用于大数据下的应用场景.

2013年Dong等人提出了第1个可处理集合元素达到亿级别大小的PSI协议[75]，该协议基于布隆过滤器(Bloom filter, BF)[76]、秘密共享和扩展不经意传输协议，主要依赖于高效的对称加密操作.布隆过滤器主要用来判断一个元素是否在集合中，通过引入一定的假阳率来节省大量的存储空间.由于2个集合的布隆过滤器结构直接进行与运算BFc∩BFs的结果和集合交集表示成布隆过滤器BFc∩s的结果不一致，通过逻辑与运算求集合交集会泄露集合中的信息，因此作者采用OT协议来保证安全性.该协议的过程为：客户端将集合n个元素表示为布隆过滤器结构(布隆过滤器本质为长度为m的位向量，每个集合元素用k个不同的Hash函数{h1,h2,…,hk}映射到位向量)；服务器端将集合元素表示为GBF(garbled Bloom filter)结构，GBF与BF本质相同，区别在于索引位置存储的是元素基于异或操作的秘密共享份额ri，即x=r1⊕r2⊕…⊕rk，x为长度为σ位的集合元素；双方执行m次OT协议，客户端的BF结构作为选择向量，服务器端的GBF结构为输入数据，由于2方采用相同的Hash函数映射，相同的元素映射到BF和GBF上的索引位置一定相同，因此经过OT协议，客户端能得到交集中元素的秘密共享份额，进一步通过查询算法可获得集合交集中元素.该协议示意过程如图1所示:

2016年Rindal等人对文献[75]中协议的恶意模型进行修正，针对恶意的客户端，采用cut and choose技术来保证协议的安全并同样采用随机OT减少服务器端通信复杂度[77].

2014年Pinkas等人在文献[73]中除了对混乱电路协议优化外，也对Dong提出的协议[75]进行优化,使用随机OT协议代替扩展OT协议,服务器端不需要保存GBF结构，节省了大量空间.具体而言，客户端和服务器端分别生成各自集合的布隆过滤器BFc,BFs，并作为m次随机OT的输入，输出分别为Gc,Gs，在每一次二选一OT计算中，如果BFc[i]=BFs[i]=1,那么Gc[i]=Gs[i]=randomstring∈{0,1}；对于∀xi∈X,yj∈Y，客户端计算maskc[i]=服务器端计算masks[j]=并发送给客户端；客户端检查是否存在j满足masks[j]=maskc[i]来判断元素xi是否在交集中.由于随机OT比OT扩展协议有更低的计算和通信复杂度，优化后的协议效率提升达到55%～60%.

基于Hash和随机OT协议的PSI协议的计算和通信复杂度和元素的位长度σ成正比，为了进一步减少计算和通信开销，2015年Pinkas等人基于置换Hash的思想，又提出了效率更高的PSI协议[78].该协议采用置换Hash[79]算法，主要思想是将元素x表示为左右2部分x=xL|xR,|xL|=logβ，左半部分主要用来表示元素索引位置p(x)=xL⊕f(xR)，其中f为随机函数:[1…2|xR|]→[1…2|xL|]，右半部分为Hash桶中实际存储的元素部分.Hash桶中只需要存储σ-logβ比特的元素，因此改进的PSI协议可以将一次元素相等性判别过程中随机OT子协议的执行次数从σ减少为σ-logβ，这进一步降低了协议的计算和通信复杂度.

基于不经意传输的PSI协议其效率主要依赖于OT子协议的效率，通过采用N选一OT协议，可进一步减少OT协议执行的次数.在Kolesnikov等人提出的N选一OT协议中[33],采用Walsh-Hadamard(WH)错误纠正码对选择向量进行编码，使得对长度为σ位的元素进行相等性判断时可以将随机OT协议执行次数从σ次减少为t次，其中t=σ/logN，但该协议只适用于较小的N，如N=256. 2016年Kolesnikov等人又提出一种新的协议[80],该协议对选择向量采用伪随机编码的方式，使元素相等性判断执行的OT协议的次数不依赖于σ，即通过一次OT协议就可以判断2个元素是否相等.作者采用固定秘钥的AES实例化伪随机函数.在σ取值为64或128时，改进的PSI协议比文献[78]中的协议快2.3～3.6 倍.

同样，为了使PSI协议的效率只与元素个数成正比而不依赖于元素的位长度σ，2016年Pinkas等人采用新的错误纠正码实现OT协议，并在此基础上改进PSI[74].因为以上PSI协议采用的都是基于随机预言模型和半诚实模型下的OT扩展协议，因此PSI协议一般适用于随机预言模型和半诚实模型.表5为基于OT的PSI协议渐进复杂度分析：

Table 5 Comparison of Private Set Intersection Protocols表5 隐私集合交集协议性能比较

Note：n: the size of sets;κ: the symmetric security parameter;

k: the number of the Hash functions.

此外作者通过实验对比了半诚实模型下的不安全Hash的PSI和基于RSA公钥加密算法、混乱电路和OT协议的PSI.表6为文献[74]中部分实验结果，该实验中用到的2台设备为Intel Haswell i7-4770K，3.5 GHz CPU 16 GB内存，通过OpenSSL(v.1.0.1e)密码学库实现论文中的对称加密操作，Miracl(v.5.6.1)和GMP库(v.5.1.2)实现OT扩展协议和公钥加密操作*https://github.com/encryptogroup/PSI，通过实验结果我们可以对各类协议的性能有更直观的认识.

Table 6 Comparison of Private Set Intersection Protocols [74]表6 集合交集协议性能比较

Note： Protocols on sets with 220over Gigabit LAN.σis 32 b and the security parameter is 128 b.

Fig. 2 Outsourced private set intersection protocol图2 外包的隐私集合交集协议

通过表6可以分析出基于公钥加密的协议计算复杂度最高，但是具有较小的通信复杂度，适用于参与方计算能力较强但是通信带宽为瓶颈的情景；基于电路和GBF的协议计算复杂度优于基于公钥的协议，但是通信复杂度最高；基于OT和Hash策略的PSI协议在计算和通信复杂度上都达到了和不安全Hash一样的量级，既满足安全性要求又达到较高的计算效率，适合处理大数据量问题.以上分析结果反映出了PSI协议的效率直接取决于底层基础协议的效率.

此外，从2个角度对协议的适用性进行分析:1)大规模场景适用性分析.基于混乱电路的协议需要将电路提前构建并全部加载到内存中，当集合很大时会有内存限制；同样对于布隆过滤器的协议也需要加载全部布隆过滤器结构到内存，因此此类协议不适合处理大数据应用问题.2)并行性分析.基于公钥加密的PSI处理单元为相互独立的元素因此可以并行化加速计算；基于混乱电路的PWC，OPRF协议可并行化处理，而SCS协议中门电路都是相互关联的不适合并行化计算；基于OT的PSI协议由于底层基础模块OT扩展协议的可并行化因此也可以进行并行计算.

3 云辅助的PSI

传统PSI协议主要是参与方之间交互完成集合交集计算，然而，有限存储资源和计算资源的终端设备和移动设备无法应对大规模数据集的PSI计算需求.与此同时，随着云计算应用的兴起，大量的存储资源和计算资源以一种按需服务的方式向用户提供，使得大量的应用借助于第三方云计算框架来完成计算.因此研究者提出了新的借助于云服务器的安全函数计算问题[36].其中，外包的隐私集合交集(OPSI)协议作为特殊的云辅助的安全函数计算问题是指存在一个不可信的第三方服务提供商P，参与方采取一系列方式将输入集合加密盲化处理(如同态加密、伪随机函数、Hash函数等)后上传到云端，然后由P在密文上完成集合交集的计算，在协议执行过程中P没有获得任何输入输出信息，主要是利用云服务器的存储和计算资源.

相比于传统的PSI协议，在设计云辅助的PSI协议时，一般需要满足抗合谋性，因为如果服务器和某一参与方进行合谋，将退化为参与方之间计算能力相差悬殊的传统的安全多方计算协议[81].外包的隐私集合交集协议示意图如图2所示，其中一部分协议设计需要可信的第三方生成共享秘钥信息.

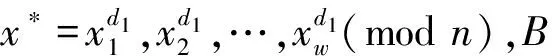
Kerschbaum等人又提出了另一种采用布隆过滤器和同态加密实现的PSI协议[83].协议过程为：客户端将集合表示成布隆过滤器结构并采用同态加密技术将布隆过滤器加密后外包给服务器；第三方服务提供商利用加密的布隆过滤器Enc(BFA),Enc(BFB)求集合交集并将集合交集的布隆过滤器结构的密文Enc(BFA∩B)返回给客户端，客户端用户对收到的密文解密并结合本地的集合即可计算集合交集.该协议在密文上进行计算主要采用SYY技术，SYY技术[84]是一种在密文上进行某种运算对应于明文的逻辑与运算的技术，在该协议中体现为通过加密布隆过滤器的与运算求明文集合信息，即Enc(BFA)*Enc(BFB)=Enc(BFA∩B),*表示秘文运算.

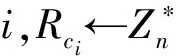
2014年Liu等人提出了一种相对简单但是会泄露集合交集基数的PSI协议[85]，该协议过程为：客户端用户分别各自生成协议中采用的对称和非对称加密算法秘钥；客户端用户生成随机数rI,rI∈，作用在数据集的Hash值上并对随机数和原始数据集进行对称加密Enc(rI);Enc(SI)，将VI,Enc(rI);Enc(SI)上传给云服务器；客户端用户与服务器端进行交互使服务器获得CI=VI+rA+rB，通过计算|CA-CB|是否为0判断元素是否属于交集.该协议是半诚实模型下可证明安全的，但是同不安全Hash协议一样存在暴力破解的风险.2015年Zheng等人提供了一种可验证机制PSI[86].

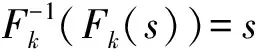
2016年李顺东等人利用哥德尔编码和ElGamal同态加密算法构造了一种半诚实模型下适用于云计算的集合交集计算方案[89].该方案解决了多个集合间的交集并集问题，但不能解决2个集合间的交集问题.

表7为云辅助PSI协议的计算和通信渐进复杂度分析.分析结果如下：

Table 7 Comparison of Private Set Intersection Protocols表7 集合交集协议性能比较

Note：exps denotes modular exponentiations operation; sym: symmetric cryptographic operations; add denotes modular additional operation;m=max(v,w)k: the number of the Hash functions.

通过对以上具体协议的分析，目前已有的云辅助PSI主要采用公钥加密和私钥加密2种类型，在协议的安全性和高效性上各具有很鲜明的特点，其中Kamara提出的协议全部采用对称加密操作，计算复杂度最低，适合大规模数据集计算，但是不能抵抗第三方服务器和参与方的合谋攻击；其他的采用同态加密等公钥加密算法对数据集进行加密计算的PSI协议，计算复杂度较高但是达到了较高的安全性，可抵抗合谋攻击.此外，传统的PSI协议一般可以经过简单调整转化为云辅助的PSI协议，在采用相同的底层密码学技术实现PSI协议时，2类协议的复杂度基本不会有很大偏差.

4 PSI应用场景

从参与方的角度考虑，PSI协议应用场景可以分为2类：1)场景中参与方均是大型企业或医疗政府军事机构等，都拥有大量隐私、有价值和具有核心竞争力的数据，双方通过安全协作计算在保护自身数据隐私性的同时达到信息共享的目的；2)场景中参与方是不对等的关系，其中一方是通过收集用户的隐私数据来提供更好服务的企业，一方是享受服务的用户，双方通过安全协作计算是为了提供/享受服务的同时保护用户隐私.因此PSI的研究具有重要意义，一方面促进具有利益冲突的企业、机构等更好的进行合作；另一方面减轻大数据时代隐私泄露问题带来的危害.对5个典型的应用场景简要说明:

1) 隐私保护相似文档检测.隐私保护相似文档检测技术主要应用于如医疗病历共享、一稿多投行为审查等.例如会议或者期刊组织方在收到提交稿时，希望在其他会议或期刊检查一下作者是否存在一稿多投现象.但通常未发表的提交稿是不能对其他会议或期刊组织者公开的，针对这个问题可以通过隐私保护相似文档检测协议进行计算，首先将双方的文档表示成文档指纹集合，通过PSI协议求得2篇文档的指纹集合交集，进而计算集合的Jaccard距离得到2篇文档的相似度[90].

2) 安全的人类基因检测.人类基因测序研究及其应用越来越普遍，在很多医疗行业有广泛的应用，比如疾病预测、个人医疗、亲子鉴定等.基因信息的共享和交换有利于加速科学研究发展，提升人类医疗保健质量，不少基因组织通过基因工程项目比如Personal Genome Project和HapMap致力于建立庞大的公共基因数据库.然而，基因信息中也包含大量的个人隐私，比如人种信息、显性体征以及疾病信息等，基因数据滥用或者非法散播会造成严重的隐私泄露.为了实现在基因数据上隐私保护的信息共享，Baldi等人基于PSI-CA，APSI和PSI协议构建了有效的基因数据隐私保护计算算法，并应用在亲子鉴定、个人医疗和基因兼容测试等场景上[22].

3) 在线广告转化率评估.在线广告作为企业营销策略的重要组成部分，蕴藏着巨大的商机.传统的评估广告影响力指标是广告点击率，但是随着人们对广告了解的深入，点击人数越来越少，点击率不能真正反映广告的效果.针对这个问题提出了广告转化率这个指标，指受网络广告影响而发生购买、注册或信息需求行为的浏览者占总广告点击人数的比例，用来反映网络广告对产品销售情况影响程度.然而广告浏览数据、交易完成数据分别掌握在广告商如谷歌、Facebook手中和商家手中，这些数据都包含有顾客的隐私信息，不能在明文信息进行交集计算，因此，可以通过信用卡号、email地址等身份表示信息进行PSI计算，在保护顾客隐私的同时实现对在线广告转化率的评估.

4) 私有联系人发现.很多手机社交类的APP要求访问新注册用户的手机通信录，通过对比通信录和APP服务器的注册用户，给新用户推荐共同使用该APP的好友.但是允许APP访问用户的手机通信录会将用户所有的联系人信息暴露给APP服务商，存在很大的隐私泄露问题.通过在APP手机端和APP服务器端运行PSI协议，计算手机通信录和服务器已注册用户集之间的交集，可以在不泄露用户隐私信息的条件下进行联系人及好友推荐[91].

5) 隐私保护的近邻检测.近邻检测是社交网络中基于位置服务的一种重要应用，但位置服务在给人们带来方便的同时也面临着严重的位置隐私泄露问题.隐私保护的近邻检测可以通过同态加密等技术实现对精准位置数据的密文计算，也可以通过WiFi、蓝牙、GPS等信号给位置打上的标签信息进行隐私集合交集计算，完成对近邻关系的评估[23].

5 总 结

随着信息化和网络化的不断发展，隐私保护成为一个越来越重要的课题，不仅关系到公民个人利益更关乎到国家的安全.安全多方计算作为隐私保护的一个重要密码学研究方法，也由最初的采用通用协议解决安全函数计算问题发展到设计特殊的针对具体问题的高效协议.PSI作为安全多方计算的一个重要应用问题，近年来也得到快速发展.目前，为了适应大数据时代的计算需求，PSI协议的发展历程主要由最初的基于公钥加密机制到基于混乱电路、不经意传输协议，以及新的计算模式——云计算环境下的协议设计.无论是传统的方法还是云辅助的PSI协议，对该问题的主要研究趋势是均衡安全性和高效性、可扩展性，研究思路主要是由最初的基于公钥加密机制到依赖更多的对称加密操作.

虽然对PSI协议的研究取得了一定的进展，但是现有协议普遍存在一些问题：1)在恶意模型下，为了验证输入数据的一致性等导致计算通信代价高，不具有实用性；2)大多数传统的高效的PSI协议主要依赖于备受争议的随机预言模型，随机预言模型的安全性证明并不能保证实际方案的安全性.

结合当前PSI问题的研究进展，未来对PSI协议研究的重点包括：1)新的不可信计算模式云计算环境下的PSI安全协议研究，随着更多公司和个人对云计算的使用，基于云计算服务的PSI协议将成为热点研究问题；2)在当前大数据背景下，已有的PSI协议尽管已经取得了很大的突破但仍有性能上的瓶颈，未来需要设计出更高效的协议来满足大数据隐私保护需求.

[1] Fang Binxing, Jia Yan, Li Aiping, et al. Privacy preservation in big data: A survey[J]. Big Data Research, 2017, 2(1): 1-18 (in Chinese)

(方滨兴, 贾焰, 李爱平, 等. 大数据隐私保护技术综述[J]. 大数据, 2017, 2(1): 1-18)

[2] Du Wenliang, Atallah M. Secure multi-party computation problems and their applications: A review and open problems[C] //Proc of the 2001 Workshop on New Security Paradigms. New York:ACM, 2001: 13-22

[3] Mu Bin. A survey on secure processing of similarity queries[OL]. (2014-05-01) [2017-09-06]. https://pdfs.semantics cholar.org/d602/831fc377fd9b84366c3e8a5ab736c9c3a5ef.pdf

[4] Erkin Z, Franz M, Guajardo J, et al. Privacy-preserving face recognition[G] //LNCS 5672: Proc of Int Symp on Privacy Enhancing Technologies. Berlin: Springer, 2009: 235-253

[5] Jagannathan G, Wright R N. Privacy-preserving distributedk-means clustering over arbitrarily partitioned data[C] //Proc of the 18th ACM SIGKDD Int Conf on Knowledge Discovery in Data Mining. New York: ACM, 2005: 593-599

[6] Bringer J, Chabanne H, Favre M, et al. GSHADE: Faster privacy-preserving distance computation and biometric identification[C] //Proc of the 2nd ACM Workshop on Information Hiding and Multimedia Security. New York: ACM, 2014: 187-198

[7] Yao A C-C. Protocols for secure computations[C] //Proc of the 23rd Annual Symp on Foundations of Computer Science (SFCS’82). Piscataway, NJ: IEEE, 1982: 160-164

[8] Goldreich O, Micali S, Wigderson A. How to play any mental game, or a completeness theorem for protocols with an honest majority[C] //Proc of the 19th Annual ACM STOC. New York: ACM, 1987: 218-229

[9] Goldreich O. Secure multi-party computation[J]. 1998 (2002-10-27) [2017-09-06]. http://www.wisdom.weizmann.ac.il/～oded/PSX/prot.pdf

[10] Goldwasser S. Multi party computations: Past and present[C] //Proc of the 16th Annual ACM Symp on Principles of Distributed Computing. New York: ACM, 1997: 1-6

[11] Kissner L, Song D. Privacy-preserving set operations[G] //LNCS 3621: Proc of Annual Int Cryptology Conf. Berlin: Springer, 2005: 241-257

[12] Sang Yingpeng, Shen Hong. Efficient and secure protocols for privacy-preserving set operations[J]. ACM Trans on Information and System Security, 2009, 13(1): 1-35

[13] Lindell Y, Pinkas B. Secure multiparty computation for privacy-preserving data mining[J]. Journal of Privacy and Confidentiality, 2009, 1(1): 59-98

[14] Agrawal R, Srikant R. Privacy-preserving data mining[C] //Proc of the 2000 ACM SIGMOD Int Conf on Management of Data Record. New York: ACM, 2000: 439-450

[15] Aggarwal C C, Philip S Y. A General Survey of Privacy-Preserving Data Mining Models and Algorithms[M]. Berlin: Springer, 2008: 11-52

[16] Pinkas B. Cryptographic techniques for privacy-preserving data mining[J]. ACM SIGKDD Explorations Newsletter, 2002, 4(2): 12-19

[17] Cao Ning, Wang Cong, Li Ming, et al. Privacy-preserving multi-keyword ranked search over encrypted cloud data[J]. IEEE Trans on Parallel and Distributed Systems, 2014, 25(1): 222-233

[18] Wang Cong, Cao Ning, Li Jin, et al. Secure ranked keyword search over encrypted cloud data[C] //Proc of the 30th Int Conf on Distributed Computing Systems (ICDCS). Piscataway, NJ: IEEE, 2010: 253-262

[19] Song D X, Wagner D, Perrig A. Practical techniques for searches on encrypted data[C] //Proc of the 2000 IEEE Symp on Security and Privacy. Piscataway, NJ: IEEE, 2000: 44-55

[20] Atallah M, Du Wenliang. Secure multi-party computational geometry[G] //LNCS 2125: Proc of Workshop on Algorithms and Data Structures (WADS 2001). Berlin: Springer, 2001: 165-179

[21] Vaidya J, Clifton C. Privacy preserving association rule mining in vertically partitioned data[C] //Proc of the 8th ACM SIGKDD Int Conf on Knowledge Discovery and Ddata Mining. New York: ACM, 2002: 639-644

[22] Baldi P, Baronio R, De Cristofaro E, et al. Countering gattaca: Efficient and secure testing of fully-sequenced human genomes[C] //Proc of the 18th ACM Conf on Computer and Communications Security. New York: ACM, 2011: 691-702

[23] Narayanan A, Thiagarajan N, Lakhani M, et al. Location privacy via private proximity testing[C] //Proc of the Network and Distributed System Security Symp. Reston, VA: ISOC, 2011

[24] Mezzour G, Perrig A, Gligor V, et al. Privacy-preserving relationship path discovery in social networks[G] //LNCS 5888: Proc of Int Conf on Cryptology and Network Security. Berlin: Springer, 2009: 189-208

[25] Freedman M J, Nissim K, Pinkas B. Efficient private matching and set intersection[G] //LNCS 3027: Proc of Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2004: 1-19

[26] Kamara S, Mohassel P, Raykova M, et al. Scaling private set intersection to billion-element sets[G] //LNCS 8437: Proc of Int Conf on Financial Cryptography and Data Security. Berlin: Springer, 2014: 195-215

[27] Goldreich O. Foundations of Cryptography Ⅱ Basic Applications[M]. Cambridge, UK: Cambridge University Press, 2004

[28] Katz J, Lindell Y. Introduction to Modern Cryptography[M]. New York: CRC Press, 2014

[29] Even S, Goldreich O, Lempel A. A randomized protocol for signing contracts[J]. Communications of the ACM, 1985, 28(6): 637-647

[30] Impagliazzo R, Rudich S. Limits on the provable consequences of one-way permutations[C] //Proc of the 21st Annual ACM Symp on Theory of Computing. New York: ACM, 1989: 44-61

[31] Beaver D. Correlated pseudorandomness and the complexity of private computations[C] //Proc of the 28th Annual ACM Symp on Theory of Computing. New York: ACM, 1996: 479-488

[32] Ishai Y, Kilian J, Nissim K, et al. Extending oblivious transfers efficiently[G] //LNCS 2729: Annual Int Cryptology Conf. Berlin: Springer, 2003: 145-161

[33] Kolesnikov V, Kumaresan R. Improved OT extension for transferring short secrets[G] //LNCS 8043: Advances in Cryptology (CRYPTO 2013). Berlin: Springer, 2013: 54-70

[34] Asharov G, Lindell Y, Schneider T, et al. More efficient oblivious transfer and extensions for faster secure computation[C] //Proc of the 2013 ACM SIGSAC Conf on Computer & Communications Security. New York: ACM, 2013: 535-548

[35] Yao A C C. How to generate and exchange secrets[C] //Proc of the 27th Annual Symp on Foundations of Computer Science. Piscataway, NJ: IEEE,1986: 162-167

[36] Kamara S, Mohassel P, Riva B. Salus: A system for server-aided secure function evaluation[C] //Proc of the 2012 ACM Conf on Computer and Communications Security. New York: ACM, 2012: 797-808

[37] Jiang Han, Xu Qiuliang. Advances in key techniques of practical secure multi-party computation[J]. Journal of Computer Research and Development, 2015, 52(10): 2247-2257 (in Chinese)

(蒋瀚, 徐秋亮. 实用安全多方计算协议关键技术研究进展[J]. 计算机研究与发展, 2015, 52(10): 2247-2257)

[38] Pinkas B, Schneider T, Smart N P, et al. Secure two-party computation is practical[G] //LNCS 5912: Proc of Int Conf on the Theory and Application of Cryptology and Information Security. Berlin: Springer, 2009: 250-267

[39] Naor M, Pinkas B, Sumner R. Privacy preserving auctions and mechanism design[C] //Proc of the 1st ACM Conf on Electronic Commerce. New York: ACM, 1999: 129-139

[40] Zahur S, Rosulek M, Evans D. Two halves make a whole[G] //LNCS 9057: Proc of Annual Int Conf on the Theory and Applications of Cryptographic Techniques (EUROCRYPT 2015). Berlin: Springer, 2015: 220-250

[41] Pinkas B. Fair secure two-party computation[G] //LNCS 2656: Proc of Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2003: 87-105

[42] Malkhi D, Nisan N, Pinkas B, et al. Fairplay-secure two-party computation system[C] //Proc of the 13th Conf on USENIX Security Symp. Berkeley, CA: USENIX Association, 2004

[43] Huang Yan, Evans D, Katz J, et al. Faster secure two-party computation using garbled circuits[C] //Proc of the 20th Conf on USENIX Security Symp. Berkeley, CA: USENIX Association, 2011

[44] Liu Chang, Wang Xiao, Nayak K, et al. Oblivm: A programming framework for secure computation[C] //Proc of 2015 IEEE Symp on Security and Privacy (SP). Piscataway, NJ: IEEE, 2015: 359-376

[45] Burkhart M, Strasser M, Many D, et al. SEPIA: Privacy-preserving aggregation of multi-domain network events and statistics[C] //Proc of the 19th Conf on USENIX Security. Berkeley, CA: USENIX Association, 2010

[46] Damgård I, Geisler M, Krøigaard M, et al. Asynchronous multiparty computation: Theory and implementation[G] //LNCS 5443: Proc of Int Workshop on Public Key Cryptography. Berlin: Springer, 2009: 160-179

[47] Bogdanov D, Laur S, Willemson J. Sharemind: A framework for fast privacy-preserving computations[G] //LNCS 5283: European Symp on Research in Computer Security. Berlin: Springer, 2008: 192-206

[48] Shamir A. How to share a secret[J]. Communications of the ACM, 1979, 22(11): 612-613

[49] Blakley G R. Safeguarding cryptographic keys[C] //Proc of American Federation of Information Processing Socicties National Computer Conf. Wuhan: SCIRP, 1979: 313-317

[50] Naor M, Pinkas B. Oblivious transfer and polynomial evaluation[C] //Proc of the 21st Annual ACM Symp on Theory of Computing. New York: ACM, 1999: 245-254

[51] Paillier P. Public-key cryptosystems based on composite degree residuosity classes[G] //LNCS 1592: Proc of Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 1999: 223-238

[52] ElGamal T. A public key cryptosystem and a signature scheme based on discrete logarithms[J]. IEEE Trans on Information Theory, 1985, 31(4): 469-472

[53] Azar Y, Broder A Z, Karlin A R, et al. Balanced allocations[J]. SIAM Journal on Computing, 1999, 29(1): 180-200

[54] Freedman M J, Hazay C, Nissim K, et al. Efficient set intersection with simulation-based security[J]. Journal of Cryptology, 2016, 29(1): 115-155

[55] Pagh R, Rodler F F. Cuckoo hashing[C] //Proc of European Symp on Algorithms. Berlin: Springer, 2001: 121-133

[56] Dachman-Soled D, Malkin T, Raykova M, et al. Efficient robust private set intersection[G] //LNCS 5536: Proc of Int Conf on Applied Cryptography and Network Security. Berlin: Springer, 2009: 125-142

[57] Zhou Sufang, Li Shundong, Guo Yimin, et al. Efficient set intersection problem computation[OL].[2017-06-01]. http://kns.cnki.net/KCMS/detail/11.1826.TP.20170526.1938.014.html (in Chinese)

(周素芳, 李顺东, 郭奕旻, 等. 保密集合相交问题的高效计算[OL]. [2017-06-01]. http://kns.cnki.net/KCMS/detail/11.1826.TP.20170526.1938.014.html)

[58] Chen Zhenhua, Li Shundong, Huang Qiong, et al. Protocols for secure computation of two set-relationships with the unencrypted method[OL]. [2017-06-01]. http://kns.cnki.net/KCMS/detail/11.2560.TP.20170331.2154.001.html (in Chinese)

(陈振华, 李顺东, 黄琼, 等. 非加密方法安全计算两种集合关系[OL]. [2017-06-01]. http://kns.cnki.net/KCMS/detail/11.2560.TP.20170331.2154.001.html)

[59] Hazay C, Nissim K. Efficient set operations in the presence of malicious adversaries[G] //LNCS 6056: Proc of Int Workshop on Public Key Cryptography. Berlin: Springer, 2010: 312-331

[60] Naor M, Reingold O. Number-theoretic constructions of efficient pseudo-random functions[J]. Journal of the ACM, 2004, 51(2): 231-262

[61] Hazay C, Lindell Y. Efficient protocols for set intersection and pattern matching with security against malicious and covert adversaries[G] //LNCS 4948: Theory of Cryptography Conf. Berlin: Springer, 2008: 155-175

[62] Jarecki S, Liu Xiaomin. Efficient oblivious pseudorandom function with applications to adaptive ot and secure computation of set intersection[G] //LNCS 5444: Proc of Theory of Cryptography Conf (TCC 2009). Berlin: Springer, 2009: 577-594

[63] Dodis Y, Yampolskiy A. A verifiable random function with short proofs and keys[G] //LNCS 3386: Proc of Int Workshop on Public Key Cryptography. Berlin: Springer, 2005: 416-431

[64] Camenisch J, Shoup V. Practical verifiable encryption and decryption of discrete logarithms[G] //LNCS 2729: Proc of Annual Int Cryptology Conf (CRYPTO 2003). Berlin: Springer, 2003: 126-144

[65] Jarecki S, Liu Xiaomin. Fast secure computation of set intersection[G] //LNCS 6280: Proc of Int Conf on Security and Cryptography for Networks. Berlin: Springer, 2010: 418-435

[66] Bellare M, Namprempre C, Pointcheval D, et al. The one-more-RSA-inversion problems and the security of Chaum’s blind signature scheme[J]. Journal of Cryptology, 2003, 16(3): 185-215

[67] De Cristofaro E, Tsudik G. Practical private set intersection protocols with linear complexity[G] //LNCS 6052: Proc of Int Conf on Financial Cryptography and Data Security. Berlin: Springer, 2010: 143-159

[68] De Cristofaro E, Kim J, Tsudik G. Linear-complexity private set intersection protocols secure in malicious model[G] //LNCS 6477: Proc of Int Conf on the Theory and Application of Cryptology and Information Security. Berlin: Springer, 2010: 213-231

[69] De Cristofaro E, Tsudik G. Experimenting with fast private set intersection[G] //LNCS 7344: Proc of Int Conf on Trust and Trustworthy Computing. Berlin: Springer, 2012: 55-73

[70] Ateniese G, De Cristofaro E, Tsudik G. (If) size matters: Size-hiding private set intersection[G] //LNCS 6571: Proc of Int Workshop on Public Key Cryptography. Berlin: Springer, 2011: 156-173

[71] Huang Y, Evans D, Katz J. Private set intersection: Are garbled circuits better than custom protocols?[C] //Proc of the Network and Distributed System Security Symp. Reston, VA: ISOC, 2012

[72] Kolesnikov V, Schneider T. Improved garbled circuit: Free XOR gates and applications[G] //LNCS 5126: Proc of Int Colloquium on Automata, Languages, and Programming. Berlin: Springer, 2008: 486-498

[73] Pinkas B, Schneider T, Zohner M. Faster private set intersection based on OT extension[C] //Proc of the 23rd USENIX Security Symp. Berkeley, CA: USENIX Association, 2014: 797-812

[74] Pinkas B, Schneider T, Zohner M. Scalable private set intersection based on OT extension[OL]. [2017-06-01]. https://eprint.iacr.org/2016/930.pdf

[75] Dong Changyu, Chen Liqun, Wen Zikai. When private set intersection meets big data: An efficient and scalable protocol[C] //Proc of the 2013 ACM SIGSAC Conf on Computer & Communications Security. New York: ACM, 2013: 789-800

[76] Bloom B H. Space/time trade-offs in Hash coding with allowable errors[J]. Communications of the ACM, 1970, 13(7): 422-426

[77] Rindal P, Rosulek M. Improved private set intersection against malicious adversaries[G] //LNCS 10210: Proc of Annual Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2017: 235-259

[78] Pinkas B, Schneider T, Segev G, et al. Phasing: Private set intersection using permutation-based hashing[C] //Proc of the 24th USENIX Security Symp. Berkeley, CA: USENIX Association, 2015: 515-530

[79] Arbitman Y, Naor M, Segev G. Backyard cuckoo hashing: Constant worst-case operations with a succinct representation[C] //Proc of the 51st Annual IEEE Symp on Foundations of Computer Science (FOCS). Piscataway, NJ: IEEE, 2010: 787-796

[80] Kolesnikov V, Kumaresan R, Rosulek M, et al. Efficient batched oblivious PRF with applications to private set intersection[C] //Proc of the 2016 ACM SIGSAC Conf on Computer and Communications Security. New York: ACM, 2016: 818-829

[81] Jiang Han, Xu Qiuliang. Secure Multi-party computation in cloud computing[J].Journal of Computer Research and Development, 2016, 53(10): 2152-2162 (in Chinese)

(蒋瀚, 徐秋亮. 基于云计算服务的安全多方计算[J]. 计算机研究与发展, 2016, 53(10): 2152-2162)

[82] Kerschbaum F. Collusion-resistant outsourcing of private set intersection[C] //Proc of the 27th Annual ACM Symp on Applied Computing. New York: ACM, 2012: 1451-1456

[83] Kerschbaum F. Outsourced private set intersection using homomorphic encryption[C] //Proc of the 7th ACM Symp on Information, Computer and Communications Security. New York: ACM, 2012: 85-86

[84] Sander T, Young A, Yung M. Non-interactive crypto-computing for NC/sup 1[C] //Proc of the 40th Annual Symp on Foundations of Computer Science. Piscataway, NJ: IEEE, 1999: 554-566

[85] Liu Fang, Ng W K, Zhang Wei, et al. Encrypted set intersection protocol for outsourced datasets[C] //Proc of 2014 IEEE Int Conf on Cloud Engineering (IC2E). Piscataway, NJ: IEEE, 2014: 135-140

[86] Zheng Qingji, Xu Shouhuai. Verifiable delegated set intersection operations on outsourced encrypted data[C] //Proc of 2015 IEEE Int Conf on Cloud Engineering (IC2E). Piscataway, NJ: IEEE, 2015: 175-184

[87] Abadi A, Terzis S, Dong Changyu. O-PSI: Delegated private set intersection on outsourced datasets[C] //Proc of IFIP Int Information Security Conf. Berlin: Springer, 2015: 3-17

[88] Abadi A, Terzis S, Dong Changyu. VD-PSI: Verifiable delegated private set intersection on outsourced private datasets[G] //LNCS 9603: Proc of Int Conf on Financial Cryptography and Data Security. Berlin: Springer, 2016: 149-168

[89] Li Shundong, Zhou Sufang, Guo Yimin, et al. Secure set computing in cloud environment[J].Journal of Software, 2016, 27(6): 1549-1565 (in Chinese)

(李顺东, 周素芳, 郭奕旻, 等. 云环境下集合隐私计算[J]. 软件学报, 2016, 27(6): 1549-1565)

[90] Blundo C, De Cristofaro E, Gasti P. EsPRESSO: Efficient privacy-preserving evaluation of sample set similarity[J]. Journal of Computer Security, 2014, 22(3): 355-381

[91] Huang Yan, Chapman P, Evans D. Privacy-preserving applications on smartphones[C] //Proc of the 6th USENIX Conf on Hot Topic in Security. Berkeley, CA: USENIX Association, 2011

SurveyonPrivatePreservingSetIntersectionTechnology

Shen Liyan1,2, Chen Xiaojun2, Shi Jinqiao2, and Hu Lanlan2

1(SchoolofCyberSecurity,UniversityofChineseAcademyofSciences,Beijing100049)2(InstituteofInformationEngineering,ChineseAcademyofSciences,Beijing100093)

The private set intersection (PSI) is a specific application problem that belongs to the field of secure multi-party computation. It not only has important theoretical significance but also has many application scenarios. In the era of big data, the research on this problem is in accord with people’s increasing privacy preserving demands at the same time to enjoy a variety of services. This paper briefly introduces the basic theory of secure multi-party computation, and highlights the two categories of current mainstream research methods of PSI under the framework of secure multi-party computation: the traditional PSI protocols based on the public key encryption mechanism, garbled circuit, oblivious transfer and the outsourced PSI protocols based on the untrusted third party service provider. Besides, we have briefly summarized the characteristic, applicability and complexity of those protocols. At the same time, the application scenarios of privacy preserving set intersection problem are also explained in detail, which further reflects the practical research value of the problem. With the deep research on the PSI problem, researchers have designed a set of private protocols that can quickly complete set intersection of millions of elements in the semi-honest model.

private set intersection (PSI); secure multi-party computation; oblivious transfer; garbled circuit; oblivious pseudorandom function evaluation; oblivious polynomial evaluation; cloud computing

TP309

ShenLiyan, born in 1992. PhD candidate. Her main research interests include privacy preserving, information security.

ChenXiaojun, born in 1979. PhD. Member of CCF. His main research interests include big data, privacy preserving, data security.

ShiJinqiao, born in 1978. PhD, associate professor. Member of CCF. His main research interests include network anonymous communication and network threats detection.

HuLanlan, born in 1979. PhD, research assistant. Her main research interests include big data, privacy preserving and information security.