RAKA:一种新的基于Ring-LWE的认证密钥协商协议
杨亚涛 张亚泽 李子臣 张峰娟 刘博雅
1(北京电子科技学院通信工程系 北京 100070) 2(北京印刷学院教务处 北京 102600) 3(西安电子科技大学通信工程学院 西安 710071) (yy2008@163.com)
2017-06-14;
2017-08-01
国家自然科学基金项目(61370188);“十三五”国家密码发展基金项目(MMJJ20170110);中央高校基本科研业务费专项资金项目(328201523) This work was supported by the National Natural Science Foundation of China (61370188), the State Cryptography Development Fund of the Thirteen Five-Year Plan (MMJJ20170110), and the Fundamental Research Funds for the Central Universities (328201523).
RAKA:一种新的基于Ring-LWE的认证密钥协商协议
杨亚涛1,3张亚泽1,3李子臣2张峰娟1,3刘博雅1
1(北京电子科技学院通信工程系 北京 100070)2(北京印刷学院教务处 北京 102600)3(西安电子科技大学通信工程学院 西安 710071) (yy2008@163.com)
后量子时代,基于格理论的公钥密码被认为是最有前途的抵抗量子计算机攻击的公钥密码体制.然而,相对于格上公钥加密体制和数字签名方案的快速发展,基于格上困难问题的密钥协商协议成果却较少.因此,现阶段如何构建格上安全的密钥协商协议是密码学领域具有挑战性的问题之一.针对上述问题,基于环上带错误学习问题困难假设,采用调和技术构造了一种新的认证密钥协商协议RAKA(authenticated key agreement protocol based on reconciliation technique),该方案采用格上陷门函数技术提供了单向认证功能,并且在Ring-LWE假设下证明是安全的.与现有的基于LWE的密钥协商协议相比,该方案的共享会话密钥减小为2nlogq,效率更高;同时,由于该方案的安全性是基于格上困难问题,因此可以抵抗量子攻击.
格理论;认证密钥协商;调和技术;环上错误学习问题;抗量子攻击
密钥协商协议[1-2](key agreement protocol, KA)是密码学的基本原语,允许通信双方在不安全的信道上协商出共同的会话密钥,并借助该会话密钥及相应的密码算法进行保密通信,是保证网络通信安全的重要密码学组件.Diffie-Hellman提出了第1个密钥协商协议[3],该协议也拉开了公钥密码学的序幕.自从Diffie-Hellman(DH)密钥协商协议提出以来,由于它构造结构简单并且实用,不少密码学者设计了很多基于DH的密钥协商协议.认证密钥协商协议(authenticated key agreement, AKA)是在密钥协商的基础上拥有了通信双方的认证功能,目前AKA协议已经被广泛应用于电子商务系统和电子政务系统等安全需求较高的系统中,因此对AKA协议的研究和设计具有很大的理论意义和实用价值.
后量子时代,由于基于大整数分解和离散对数问题的传统公钥密码体制容易受到量子计算机攻击,因此寻找抗量子攻击的AKA协议非常具有研究价值.后量子密钥协商协议已经被美国国家标准技术研究院(National Institute of Standards and Technology, NIST)作为一项重大科研项目.格理论(Lattice)是设计后量子安全公钥密码方案的重要理论,基于格理论设计的密码方案具有抗量子计算机攻击、计算效率高、可证明安全等优势.因此,基于格理论的公钥密码方案是后量子时代最具潜力替代传统基于数论难题的密码方案.2009年Regev提出错误学习(learning with errors, LWE)困难问题,并指出求解平均困难问题LWE的难度可以规约到求解格上最坏情况下困难问题[4].自从Regev提出LWE困难问题以来,由于该困难问题的困难性和良好的代数结构,在密码方案的构造方面已经得到了广泛应用.基于格的公钥加密方案[5]、数字签名方案[6-7]已经得到了很好的发展,格理论也有可能成为设计后量子安全密码方案的依据.
相比基于格的加密、数字签名方案,基于格的认证密钥协商协议(lattice-based AKA, LBAKA)发展起步较晚.目前,设计后量子安全的AKA主要存在2方面思路:1)直接基于错误学习问题LWE和小整数解问题(small integer solution, SIS)的不同形式来直接构造认证密钥协商协议.2)基于密钥封装(key encapsulation mechanism, KEM)与调和技术来构造密钥协商协议.自从2012年丁津泰首次提出一种基于LWE的密钥协商协议[8]以来,基于LWE,RLWE的密钥协商协议得到了发展,成果颇多.2014年丁津泰等人根据矩阵乘法满足结合律,使用LWE困难问题构造了密钥协商协议,并扩展到Ring-LWE上[9].在EURPCRYPT 2015上,张江等人首次提出了基于理想格上两轮认证密钥协商协议[10],该协议是基于Ring-LWE困难问题构造的,并且证明了该方案在加强的BR模型下是安全的.同年,杨孝鹏等人[11]基于Ring-DLWE困难问题提出了认证密钥协商协议,并证明方案是CK模型中可证明安全的.
本文利用调和技术(reconciliation technique,RT)基于Ring-LWE困难问题设计了一轮的单向认证密钥协商算法.
1 预备知识
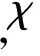
LWE问题就是从上述方程组中求出s.
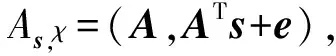
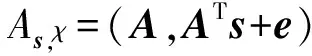
定义2. 环上带误差的学习问题(RLWE).定义
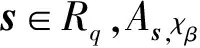
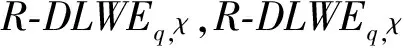
2) RLWE搜索问题(RLWE search).给定概率分布bi=ai,s+ei,以不可忽略的概率输出
定义3. 调和技术(reconciliation technique).调和技术是Peikert在文献[12]中首次提出的,该方法思路来源于Ding等人提出的调和方法,Peikert在此基础上进行了改进,提出了新的调和技术.
1) 当p=2,q是偶数时:
任取x∈,定义x=x+∈,xp


·2×vmod 2,
则对于所有的元素v∈q,I0和I1给出了一个划分,即当v∈I0或v∈I1,有v2=0;对于另一种划

下面定义调和函数rec:q×2→2,
rec(ω)
其中,E,如果v,ω∈q非常接近,那么给定ω和v2,我们可以恢复出v2,利用上述原理可以得到结论:
对于偶数q,如果对于v∈q,e∈E,ω=v+e(modq),则rec(ω)=v2.
2) 对于奇数q,定义随机化函数dbl:q→2q,如果v∈q是随机均匀的则2=rec(ω)是随机均匀的.
上述结论是对于q为偶数时,但是在RLWE的实际应用中考虑到方案的安全性,q往往被设定为充分大的素数.
2 方案描述
考虑多项式环R=[x]f(x),其中f(x)=xn+1,其中n为2的幂次方,令Rq=RqR,则Rq中的元素可以表示为
f(x)=a0+a1x+…+an-1xn-1.
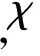
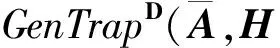
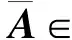
① 从高斯分布D中选取矩阵R∈q;

RAKA方案流程如图1所示:

Fig. 1 Flow process of RAKA图1 RAKA方案流程
图1详细流程说明如下:
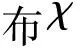
3) Alice收到(cB,pB)后,首先利用陷门TA和cB使用表2中算法2恢复s2和e2,验证Bob的身份[13],如果验证不通过,则终止;如果通过,则计算共享密钥k1=rec(pBsA),同样Bob计算共享密钥k2=rec(pAsB).
算法2. 陷门函数求逆算法InvertO(R,A,b).
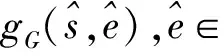
输出:向量s和e.
① 校验矩阵A∈n×mq;陷门R∈m×kn;
② 可逆标签矩阵H∈n×nq;
③ 向量bt=gA(s,e)=stA+et,e∈m,s∈nq.
3 方案的正确性
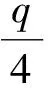
4 安全性证明
定理1. 如果Ring-LWE假设成立,则RAKA协议在被动PPT敌手攻击下是安全的.
证明. 下面我们将通过一系列的Games来证明方案的安全性.令kB=pAsB,kA=pBsA,首先Game0中的敌手得到的是真实的kB,是敌手和协议之间真实的交互,而Game4中敌手得到的是一个随机均匀地kB.下面我们证明,在Ring-LWE假设成立下,Game0到Game4对于PPT敌手是计算不可区分的.
Game0. 该游戏是在挑战者和被动敌手A之间执行的,敌手获得m,pA,pB,kA,kB,则敌手输出猜测值b′.
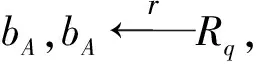
Game2. Game2与Game1大致相同,除了pB和kB的设置,挑战者将pB设置为随机值bB,将kB设置为随机值u.
Game3. Game3与Game2大致相同,挑战者在Game2的基础上,令pA=msA+eAmodq,即相比于Game2中,pA不是随机值.
Game4. 挑战者在Game3的基础上将pB=msB+eBmodq.
证毕.
引理1. 如果Ring-LWE假设成立,则Game0和Game1在被动PPT敌手攻击下是计算不可区分的.
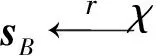
如果bA是Ring-LWE的一个样本值,则A得到的与Game0中完全一样,如果bA是一个随机均匀选取的随机值,那么A得到的与Game1中完全一样.这就意味着,如果A可以以不可忽略的概率区分Game0和Game1,那么B就可以以同样的概率来区分Ring-LWE样本和随机值.
证毕.
引理2. 如果Ring-LWE假设成立,则Game1和Game2在被动PPT敌手攻击下是计算不可区分的.
证明. 如果存在敌手A可以区分Game1和Game2,那么我们可以构造出一个PPT敌手B可以区分Ring-LWE样本与随机均匀值.针对Game1与Game2的区别,敌手B可以从Ring-LWE挑战者得到m,bB,bA,u,敌手B令pA=bA,pB=bB,kB=u,发送(m,pA,pB,kB)给敌手A.注意到,如果u和bB都是Ring-LWE的样本值,那么A得到的与Game1中完全相同.如果u和bB都是随机值,那么A得到的就与Game2中完全相同.因此,如果敌手A可以以不可忽略的概率区分Game1和Game2,那么敌手B也可以以相同的概率来区分Ring-LWE样本和随机值,从而攻破Ring-LWE困难问题.
证毕.
引理3. 如果Ring-LWE假设成立,那么Game2和Game3在被动PPT敌手攻击下是计算不可区分的.
证明. 引理3的证明可以参照引理1证明过程,需要注意的是在Game2和Game3中kB=u为随机值.
证毕.
引理4. 如果Ring-LWE假设成立,那么Game3和Game4在被动PPT敌手攻击下是计算不可区分的.
证明. 引理3的证明可以参照引理2证明过程,需要注意的是在Game3和Game4中kB也设定为随机值u.
证毕.
5 效率分析
本文主要从方案中共享密钥的大小和协商轮数考虑方案的效率.表1是本文方案与文献[8-9]的效率对比.

Table 1 Comparison Between Some Key Agreement Schemes Based on Ring-LWE表1 基于Ring-LWE密钥协商方案的性能比较
6 总 结
本文基于RLWE困难问题设计了一轮单向认证密钥协商协议,方案中使用调和技术来提供双方共享密钥.本文所设计方案的密钥尺寸减小为2nlogq,并且协商轮数也减少,但是方案实现的是单项认证.因此,下一步工作要进一步研究在此基础上如何实现双向认证的密钥协商协议.
[1] Dodis Y, Mironov I, Stephens-Davidowitz N. Message transmission with reverse firewalls-secure communication on corrupted machines[G] //LNCS 9814: Advances in Cryptology (CRYPTO 2016). Berlin: Springer, 2016: 341-372
[2] Benzvi A, Blackburn S R, Tsaban B. A practical cryptanalysis of the algebraic eraser[G] //LNCS 9814: Advances in Cryptology (CRYPTO 2016). Berlin: Springer, 2016: 179-189
[3] Diffie W, Hellman M. New directions in cryptography[J]. IEEE Trans on Information Theory, 1976, 22(6): 644-654
[4] Regev O. On Lattices, learning with errors, random linear codes, and cryptography[J]. Journal of the ACM, 2009, 56(6): 1-37
[5] Clear M, Mcgoldrick C. Multi-identity and multi-key leveled FHE from learning with errors[G] //LNCS 9216: Advances in Cryptology (CRYPTO 2015). Berlin: Springer, 2015: 630-656
[6] Ling San, Nguyen K, Wang Huaxiong. Group signatures from Lattices: Simpler, tighter, shorter, ring-based[G] //LNCS 9020: Proc of the 2015 Advances in Public Key Cryptography (PKC2015). Berlin: Springer, 2015: 427-449
[7] Gorbunov S, Vaikuntanathan V, Wee H. Predicate encryption for circuits from LWE[G] //LNCS 9216: Advances in Cryptology (CRYPTO 2015). Berlin: Springer, 2015: 503-523
[8] Ding Jintai. A simple provably secure key exchange scheme based on the learning with errors problem, 20121210: 115748[R]. New York: IACR, 2012
[9] Ding Jintai, Xie Xiang, Lin Xiaodong. A simple provably secure key exchange scheme based on the learning with errors problem, 20140729: 180116[R]. New York: IACR, 2014
[10] Zhang Jiang, Zhang Zhenfeng, Ding Jintai, et al. Authenticated key exchange from ideal Lattices[G] //LNCS 9057: Advances in Cryptology (EUROCRYPT 2015). Berlin: Springer, 2015: 719-751
[11] Yang Xiaopeng, Ma Wenping, Zhang Chengli. New authenticated key exchange scheme based on ring learning with errors problem[J]. Journal of Electronics & Informa-tion Technology, 2015, 37(8): 1984-1988 (in Chinese)
(杨孝鹏, 马文平, 张成丽. 一种新型基于环上带错误学习问题的认证密钥交换方案[J]. 电子与信息学报, 2015, 37(8): 1984-1988)
[12] Peikert C. Lattice cryptography for the Internet [G] //LNCS 8772: Proc of 2014 Post-Quantum Cryptography (PQCrypto 2014). Berlin: Springer, 2014: 197-219
[13] Micciancio D, Peikert C. Trapdoors for Lattices: Simpler, tighter, faster, smaller[G] //LNCS 7237: Advances in Cryptology (EUROCRYPT 2012). Berlin: Springer, 2012: 700-718
RAKA:NewAuthenticatedKeyAgreementProtocolBasedonRing-LWE
Yang Yatao1,3, Zhang Yaze1,3, Li Zichen2, Zhang Fengjuan1,3, and Liu Boya1
1(DepartmentofCommunicationEngineering,BeijingElectronicScience&TechnologyInstitute,Beijing100070)2(OfficeofEducationalAdministration,BeijingInstituteofGraphicCommunication,Beijing102600)3(SchoolofCommunicationEngineering,XidianUniversity,Xi’an710071)
During the post quantum era, public key cryptosystem based on Lattice is considered to be the most promising cryptosystem to resist quantum computer attack. Comparing to the rapid development of public key encryption and digital signature schemes based on Lattice, the key agreement protocols rarely appeared in the research papers. Therefore, how to construct the secure key agreement protocol is one of the most challenging problems. To solve this problem above, a secure key agreement protocol RAKA based on reconciliation technique and ring learning with errors (Ring-LWE) is designed. The proposed scheme is provably secure under the Ring-LWE assumption and can provide authentication by using the Lattice-based trapdoor function. Compared with current key agreement schemes based on LWE, this scheme is more efficient and the shared key size is reduced to 2nlogq. Moreover, this scheme can resist quantum attack because of the hard assumption on Lattice.
Lattice; authenticated key agreement (AKA); reconciliation technique; ring learning with errors (Ring-LWE); resist quantum attacks
his master degree from Xidian University. His main research interests include cryptosy-stems and information security.
TP309

YangYatao, born in 1978. Associate professor at Beijing Electronic Science and Technology Institute. Received his PhD degree from Beijing University of Posts and Telecommunications in 2009. His main research interests include information security, homomorphic cryptosystems, design of cryptographic protocol and algorithm.


LiZichen, born in 1965. Professor at Beijing Institute of Graphic Communica-tion. Received his PhD degree from Beijing University of Posts and Telecommunica-tions in 1999. His main research interests include cryptography, digital signature, design of cryptographic protocol and algorithm.

ZhangFengjuan, born in 1992. Received her master degree from Xidian University. Her main research interests include crypto-systems and information security.

LiuBoya, born in 1990. Received his master degree from Beijing Electronic Science and Technology Institute. His main research interests include crypto-systems and information security.

