物联网环境中LED轻量级密码算法的统计故障分析研究

李 玮 葛晨雨 谷大武 廖林峰 高志勇 郭 筝 刘 亚 刘志强 石秀金

1(东华大学计算机科学与技术学院 上海 201620)2(上海交通大学计算机科学与工程系 上海 200240)3(上海市信息安全综合管理技术研究重点实验室(上海交通大学) 上海 200240) 4(上海交通大学微电子学院 上海 200240)5(上海理工大学计算机科学与工程系 上海 200093) (liwei．cs．cn@gmail．com)

2017-06-11；

2017-07-31

国家“九七三”重点基础研究发展计划基金项目(2013CB338004)；国家自然科学基金项目(61672347,61772129,61402288,61402286,61402250,61572192)；上海市自然科学基金项目(15ZR1400300,16ZR1401100)；上海市教育委员会科研创新重点项目(14ZZ066)；上海市信息安全综合管理技术研究重点实验室开放课题(AGK201703)；中央高校基本科研业务费专项资金项目(040) This work was supported by the National Basic Research Program of China (973 Program) (2013CB338004), the National Natural Science Foundation of China (61672347, 61772129, 61402288, 61402286, 61402250, 61572192), the Shanghai Natural Science Foundation (15ZR1400300, 16ZR1401100), the Innovation Program of Shanghai Municipal Education Commission (14ZZ066), the Opening Project of Shanghai Key Laboratory of Integrated Administration Technologies for Information Security (AGK201703), and the Fundamental Research Funds for the Central Universities (040).

石秀金(sxj@dhu.edu.cn)

物联网环境中LED轻量级密码算法的统计故障分析研究

李 玮1,2,3葛晨雨1谷大武2廖林峰1高志勇1郭 筝4刘 亚5刘志强2石秀金1

1(东华大学计算机科学与技术学院 上海 201620)2(上海交通大学计算机科学与工程系 上海 200240)3(上海市信息安全综合管理技术研究重点实验室(上海交通大学) 上海 200240)4(上海交通大学微电子学院 上海 200240)5(上海理工大学计算机科学与工程系 上海 200093) (liwei．cs．cn@gmail．com)

LED算法是于2011年密码硬件与嵌入式系统国际会议(CHES)中提出的一种典型轻量级密码算法，用于在物联网环境下保护RFID标签以及智能卡等设备的通信安全.故障分析凭借其攻击速度快、实现简单和难以防御等特点，已成为评测轻量级密码算法安全性的一种重要手段.提出了针对LED算法的新型统计故障分析方法，采用面向半字节的故障模型，分别使用SEI区分器、GF区分器和GF-SEI双重区分器对算法进行统计分析.实验结果表明：在较短时间内以99%的成功概率恢复出LED算法的64 b和128 b原始密钥.该攻击方法不仅可以在唯密文攻击条件下实现，而且提升了故障攻击效率，降低了故障数,为物联网环境下其他轻量级密码的安全性分析提供了重要参考.

物联网；轻量级密码；LED；统计故障分析；密码分析

物联网(Internet of things, IoT)是通过使用射频识别、传感器、红外感应器、全球定位系统、激光扫描器等信息采集设备，按照约定的协议把任何物品与互联网连接起来进行信息交换和通信，以实现智能化识别、定位、跟踪、监控和管理的一种网络[1].物联网代表了未来计算与通信技术的方向，被认为是继计算机、Internet之后，信息产业领域的第三次发展浪潮.随着物联网建设的加快，物联网的安全问题必然成为制约物联网全面发展的重要因素[2].

与互联网安全技术相比，物联网安全技术更具大众性和平民性，与人类的日常生活密切相关，这就要求物联网安全技术采用低成本、简单、易用、轻量级的解决方案[3-4].在2011年召开的密码硬件与嵌入式系统国际会议(CHES)上，Guo等人提出的LED算法就是一种典型的轻量级密码算法，相较于其他轻量级密码算法，它的软硬件执行效率更高、适应环境的能力更强，是应用于物联网安全中的算法佼佼者[5-13].

在物联网环境下，轻量级密码的许多硬件实现和以硬件为表现形式的软件实现环境中，譬如手机SIM、IC银行卡、物流RFID、手持无线设备、数字无绳电话、NFC近场通信设备、蓝牙、汽车遥控锁、各类交通卡、校园卡、门禁卡和高端身份卡等密码载体等，攻击者往往不仅具备传统密码攻击的条件，而且还可以通过电路剖析和软件逆向分析等手段获得算法的硬件结构和编码实现方法，并可以观察和测量密码变换等信息，“干预”密码变换的正常运行使其出错.攻击者利用这些额外的出错信息有可能实现比传统分析技术更有效地破译密码.这种环境下的攻击被称为“故障分析(fault analysis, FA)”.由于其成功的攻击效果和潜在的发展前景，已经引起了国内外从事密码和微电子研究学者的极大关注，并成为密码分析和密码工程领域发展最为迅速的方向之一[14].

在故障分析的发展历程中，先后产生了差分故障分析(differential fault analysis, DFA)、代数故障分析(algebra fault analysis, AFA)、不可能故障分析(impossible differential fault analysis, IDFA)以及统计故障分析(statistical fault analysis, SFA)等多种方法.随着故障注入精度以及软硬件逆向技术的不断提高，对密码载体成功实施故障攻击所依赖的前提条件不断减弱，成本不断下降，故障分析环境已经在一定程度上可以控制，从而使这些故障分析在面向物联网环境中逐步发展为攻击密码体制的主要方法.

不同于其他故障分析方法，统计故障分析是唯一现有的可以在唯密文攻击(ciphertext-only attacks, COA)条件下进行攻击的技术，它在面向物联网等实际环境中更易实现且难以防御，攻击者只要统计故障密文的特性，就能以低的计算量和存储量推导出正确的密钥.目前，在LED算法抗统计故障攻击的安全性方面，国内外尚未发现有公开发表的结果.在深入分析LED算法后，本文提出了一种针对LED算法的新型统计故障分析方法，不仅提高故障导入的效率，而且使用较少的故障数即可恢复原始密钥，对于保护物联网的通信安全，对于增强密码装备的自主设计、开发和分析能力，无疑都具有重要意义和价值.

1 研究背景

1997年Boneh等人利用随机故障成功破译RSA算法，此后故障分析在评测主流密码体制安全性的方法中占据了重要的位置[14-15].故障分析的成功实现必须具备了一个重要前提——故障假设，它表明了攻击者具备的能力，决定了攻击的可行性和难易度.一般情况下，攻击者可以任意选择明文进行处理，从而获得相对应的密文，通常为选择明文攻击(chosen plaintext attacks, CPA).

在LED算法密码的故障分析中，诸如差分故障分析、代数故障分析和不可能故障分析等方法，均采用了选择明文攻击的故障假设.攻击者可以选择任意明文获得相应的正确密文和错误密文.国内外研究学者针对LED算法于2012年相继提出了差分故障分析方法，Jeong等人在随机半字节故障下破译了LED算法的64 b密钥；Li等人在随机半字节和字节模型下，至少以3个故障和6个故障恢复了64 b和128 b密钥；Jovanovic等人通过利用不同轮之间的线性关系将故障数降为1个和2个故障[16-20].2013年，Zhao等人利用代数关系，使用代数故障分析对LED算法进行了破译[21-22].2016年，Li等人利用不可能差分故障分析恢复了LED算法的64 b和128 b密钥[23].这些方法充分结合了传统密码分析技术以及软硬件实现，不仅扩大了攻击面，而且提升了威胁性.表1列出了针对LED算法的各种故障分析技术对比.

Table 1 Comparison of Fault Analysis on LED

然而，在面向物联网等现实的运行环境下，如果攻击者不具备选择明文攻击的前提，即不能实现对同一明文必须至少加密2次，则上述故障分析方法难以实现.众所周知：唯密文攻击比选择明文攻击弱，攻击者在此模型下仅能使用密文，因而无法获得有效数据进行故障分析破译.

2013年Fuhr等人首次提出了统计故障攻击方法[24],并用于破译了AES算法.该方法在唯密文攻击的假设下，在算法运行时引入故障，使算法执行某些错误的操作、过程，并产生错误的结果，再利用这些结果，结合统计分析方法，破译出该算法的密钥.在随机字节故障模型下，他们通过采用平方欧氏距离SEI作为区分器，将故障导入在倒数第二轮的指定位置，以320个故障且99%的成功概率恢复出AES算法的唯一密钥.

由此，在统计故障分析中，区分器发挥了举足轻重的作用.因此，在LED算法的新型统计分析中，我们不仅给出了SEI的攻击结果，而且提出了拟合优度检验GF作为新型区分器.更为重要的是，在SEI和GF区分器的基础上，又构建了GF-SEI双重区分器.结果表明：可以以更少的故障且99%的成功率恢复LED算法64 b和128 b原始密钥，不仅提升了故障攻击效率，而且降低了故障攻击数.

2 LED算法简介

LED算法是一种具有SPN结构的迭代型分组密码，分组长度为64 b，密钥长度分别为64 b或128 b.根据密钥长度的不同，加密算法对应的轮数分别为32轮和48轮，表示为LED -64和LED -128，如表2所示.由于解密算法与加密算法的结构相同，并且子密钥的使用顺序相同，因此以下仅介绍加密算法和密钥编排方案.

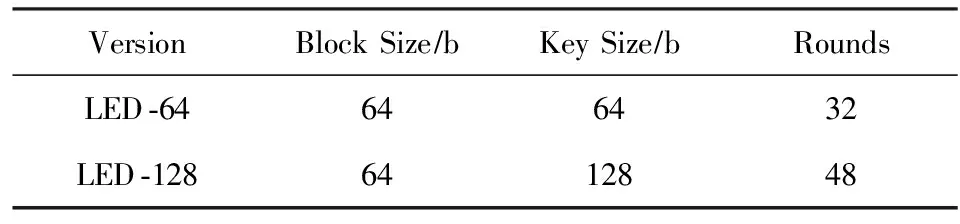
Table 2 The Relationship Between Rounds and Key Sizes

2.1符号说明

本文记号如下所示：

记AC,SC,SR和MC分别为轮常数加运算、信元代替运算、行移位运算和列混合运算.

记AC-1,SC-1,SR-1和MC-1分别为轮常数加运算、信元代替运算、行移位运算和列混合运算的逆运算.

记Ar,Br,Cr和Dr分别为第r轮的轮常数加运算、信元代替运算、行移位运算和列混合运算的输出，其中，1≤r≤l.

2.2算法描述

LED算法的结构如图1所示.

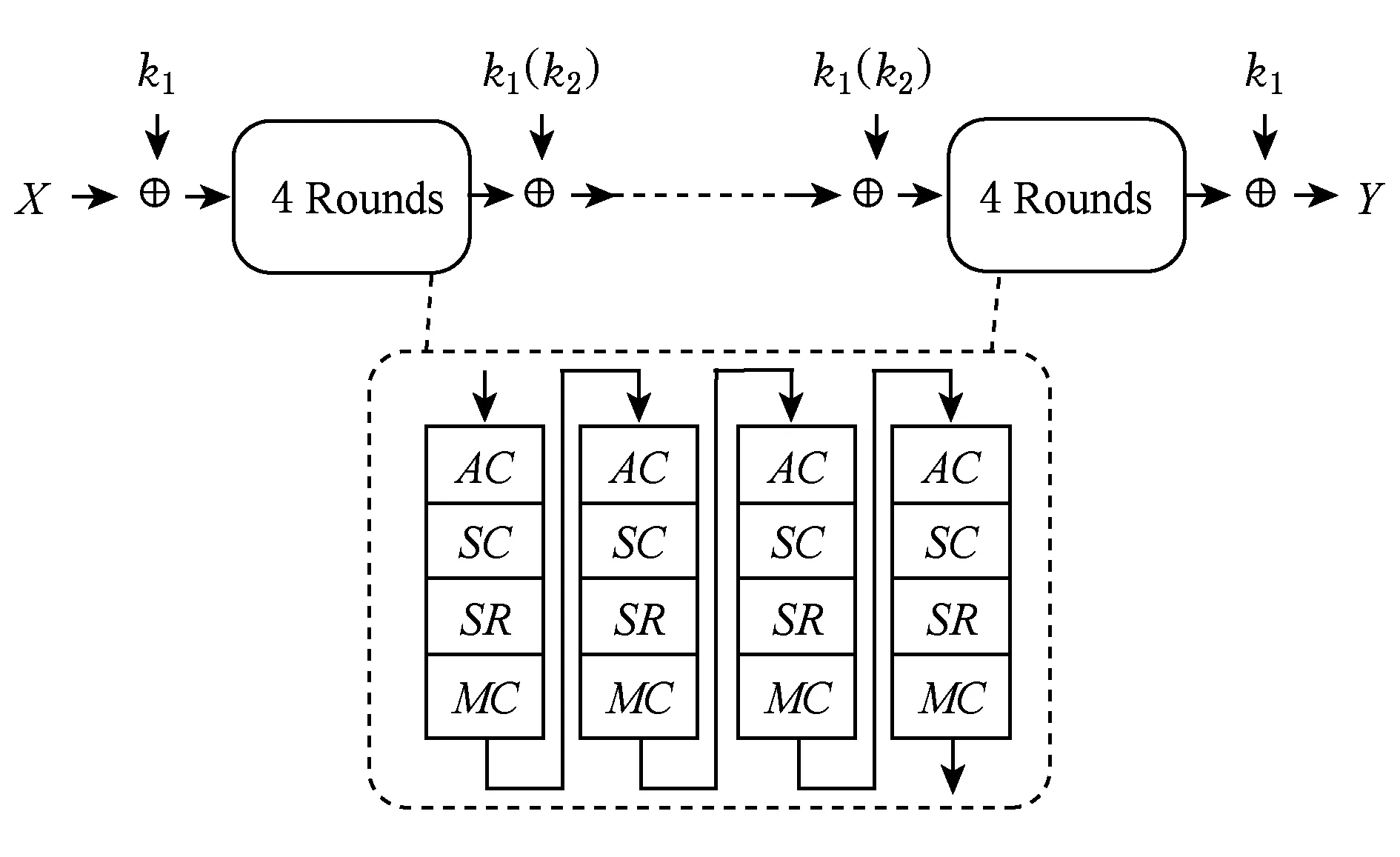
Fig. 1 The structure of LED图1 LED算法的结构

加解密算法包含5个基本运算：

1) 子密钥加运算(AddRoundKey, ARK).该运算对中间状态与子密钥进行异或.

2) 常数相加运算(AddConstants, AC).该运算将中间状态与常数相加.

3) 信元代替运算(SubCells, SC).该运算将中间状态中的每半字节通过S盒非线性地变换为另外一个半字节.

4) 行移位运算(ShiftRows, SR).该运算对一个状态的每一行循环不同的位移量.第0行移位保持不变，第1行循环左移4 b，第2行循环左移8 b，第3行循环左移12 b.

5) 列混合运算(MixColumnsSerial, MC).该运算对一个状态逐列进行变换，通过与矩阵

相乘实现.

LED -64和LED -128的加密变换分别如算法1、算法2所示.

算法1. LED -64加密变换.

输入：明文X、密钥K；

输出：密文Y.

①T=X;*将X赋值给中间状态T*

② fori=1 to 8

③T=ARK(T,k1);

④ forj=1 to 4

⑤T=MC(SR(SC(AC(T))));

⑥ end for

⑦ end for

⑧Y=ARK(T,k1).

算法2. LED -128加密变换.

输入：明文X、密钥K；

输出：密文Y.

①T=X;*将X赋值给中间状态T*

② fori=1 to 6

③T=ARK(T,k1);

④ forj=1 to 4

⑤T=MC(SR(SC(AC(T))));

⑥ end for

⑦T=ARK(T,k2);

⑧ forj=1 to 4

⑨T=MC(SR(SC(AC(T))));

⑩ end for

2.3密码编排方案

在LED -64算法中，K通过密钥编排方案生成了k1，它们的关系为

K=k1.

在LED -128算法中，K通过密钥编排方案生成了k1和k2，它们的关系为

K=k1‖k2.

对于LED -64算法，攻击者仅需要恢复出任意一轮的子密钥k1，就能恢复出密钥K；而对于LED -128算法，攻击者仅需要恢复任意一轮的子密钥k1和k2，就能恢复出密钥K.

3 LED密码的统计故障攻击方法

3.1故障假设和故障模型

故障假设为唯密文攻击,即攻击者仅能获得密码算法的任意密文进行攻击.考虑到实际应用中的易操作性以及LED算法的设计特点，本文中使用随机半字节故障模型，以按位与的方式导入，故障大小为半字节.

3.2主要过程

攻击者使用同一个密钥对随机明文进行加密,并在运行过程中的某一轮导入随机故障，获得一组错误密文.故障导入的动作可以通过软件模拟的方式实现，也可以通过激光、电磁和电压干扰等技术手段对真实的密码实现硬件进行处理来实现.由于受故障影响，加密过程中的一些中间状态值会呈现非均匀分布.利用特定的区分器统计这些中间状态值的分布律，得到最后一轮的子密钥的部分比特.重复上述步骤，可以恢复子密钥的全部比特，最终通过密钥编排方案求得原始密钥.

3.3攻击步骤

针对LED算法,本文验证了Fuhr等人提出的SEI区分器,并提出了2种新型区分器用于统计故障分析，均可以破译LED -64和LED -128算法.具体有5个步骤：

步骤1.随机生成一组明文，使用同一密钥加密，在加密过程中随机导入半字节故障，获得一组错误密文.故障导入的位置可以是Ar-1,Br-1或者Cr-1，导入在这3个位置时故障扩散路径是相同的.如图2所示，图2中阴影表示受故障影响的半字节，不同灰度的阴影表示不同比例的故障差分值.

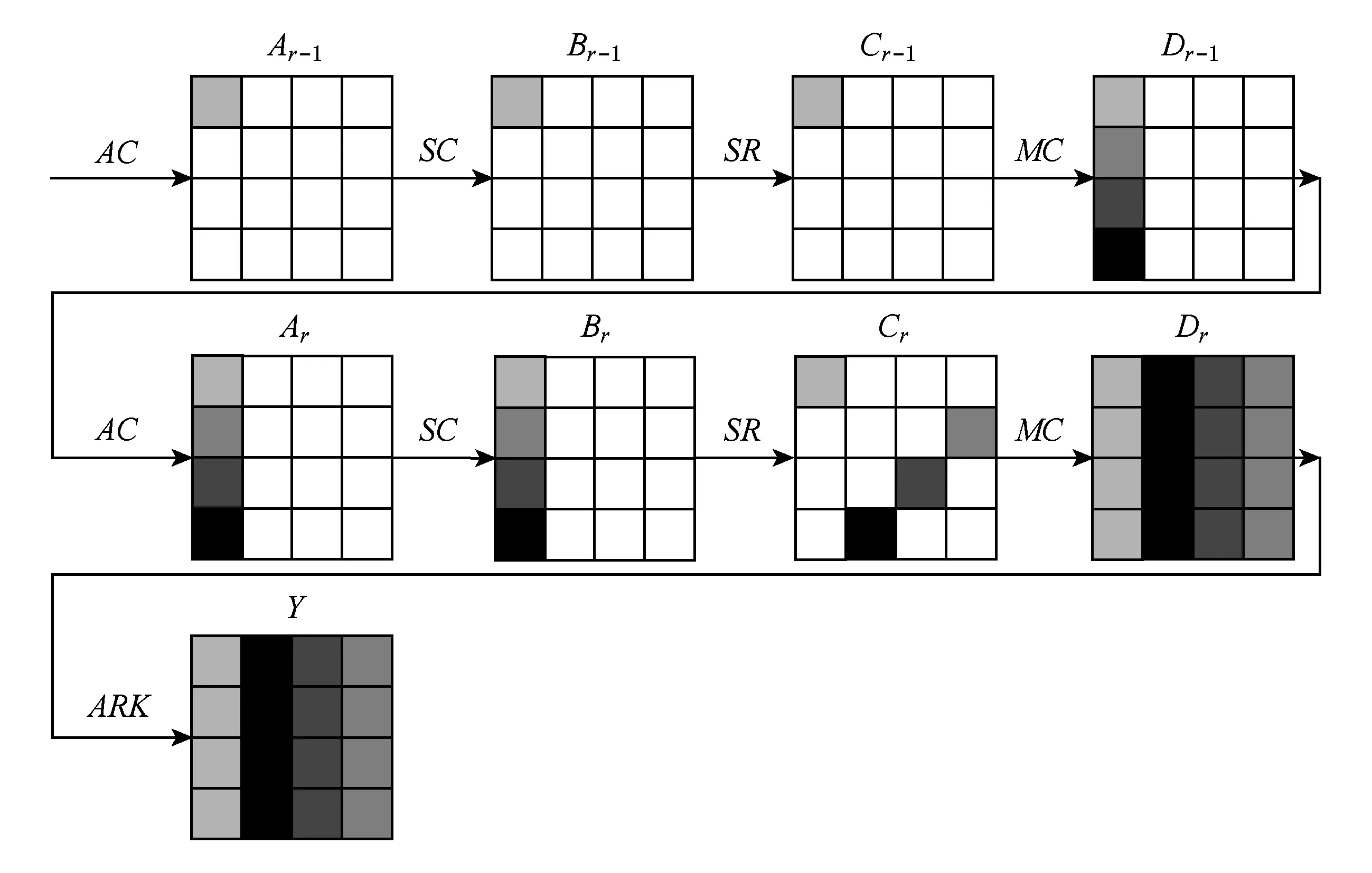
Fig. 2 Fault diffusion path in the penultimate round图2 故障导入在倒数第2轮后的扩散路径

步骤2.经过列混合变换后，中间状态的每个半字节的分布律都受到上一个中间状态的4个半字节分布律的影响.攻击者需统计未经过MC且受到故障影响的半字节的分布，即Ar-1,Br-1或者Cr-1.以Cr-1为例，通过加密算法可以得出，Cr-1的每一个半字节都能用子密钥k1和错误密文Y*的4个半字节来表示：

Cr-1=MC-1(AC-1(SC-1(SR-1(MC-1(Y*⊕
k1)))))=MC-1(AC-1(SC-1(SR-1(MC-1(Y*)⊕
MC-1(k1))))).

步骤3.通过统计分析，计算出k1的16 b.对于每一个子密钥候选值，都能求出一组Cr-1.选定一个区分器，将这组数据作为样本，求出每个候选值的区分器值，经过比较，选取区分器值最大(小)的候选值，即为正确子密钥.

本步骤中所使用的区分器有3种：

1) SEI区分器

平方欧氏距离(square Euclidean imbalance, SEI)是由Fuhr等人提出的一种统计故障分析区分器，用于判断一组样本值是否服从均匀分布.攻击者计算出最不可能服从均匀分布的那一组样本值，即可求出子密钥的部分位.表达式为

其中,γ[ε]记录了样本值为ε的样本个数；N为样本总个数；λ表示计量值的分组组数.当求得的SEI越小，表示这组样本越服从均匀分布.

2) GF区分器

拟合优度(goodness of fit, GF)作为统计故障分析新区分器之一，适用于已知样本分布率的情况下.攻击者通过计算一组样本是否满足该分布，从而求出子密钥的部分位.表达式为

其中，λ表示计量值的分组组数；Oε表示样本处于分组ε中的个数；Φε表示在相同的样本总数下，处于分组ε中的理论个数.与SEI区分器结果类似，若计算结果越小，则表示该组样本越服从该分布.

Table 3 The Overview of a Nibble After Fault Injections

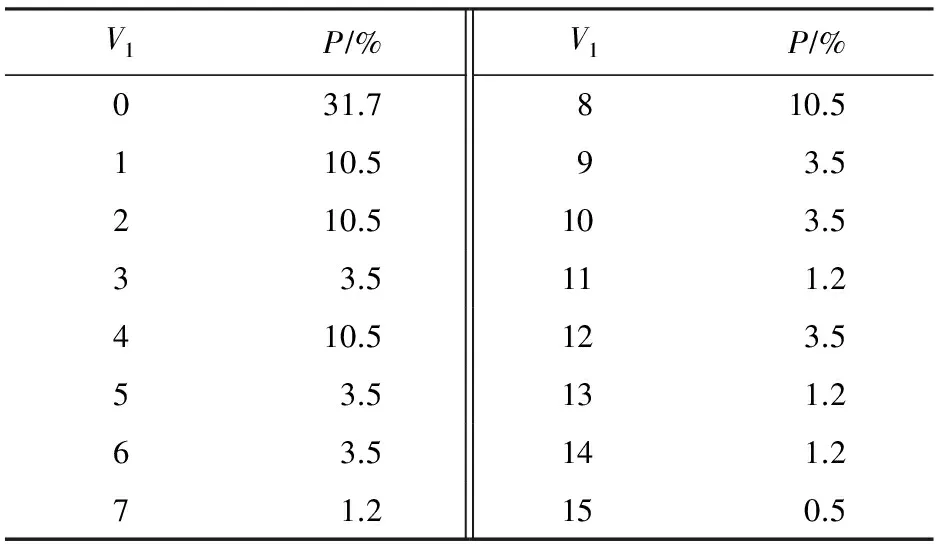
Table 4 The Distribution of a Nibble After Fault Injections

3) GF-SEI双重区分器

为了进一步减少故障数并且解决以上问题，攻击者可以将上述2个区分器结合，构建一个新型GF-SEI双重区分器.使用方法为：先用拟合优度检验筛选出符合中间状态值分布的所有样本组；再用SEI区分器从中寻找最优样本，从而恢复一定的密钥比特.

步骤4.上述过程重复4次，即可恢复出子密钥k1的全部位.LED -64的原始密钥K即可通过密钥编排算法求得.

步骤5.在破译LED -128算法时，首先按上述过程恢复子密钥k1；然后利用k1解密最后4轮，得到第44轮的输出，重复上述步骤，即恢复子密钥k2；最后根据密钥编排算法求得原始密钥K，使用故障数为LED -64算法的2倍.

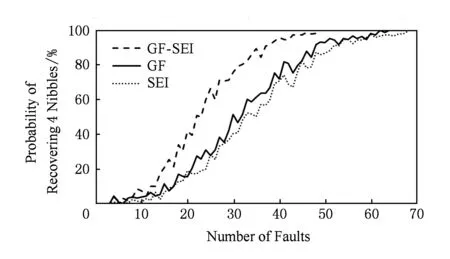
Fig. 3 The probability of recovering a partial subkey using different faults图3 使用不同故障数时恢复出部分子密钥的概率

4 实验分析

实验采用使用Eclipse平台编写Java代码进行算法的加解密和攻击操作，利用计算机软件模拟故障产生，通过随机数生成器生成随机半字节值，以按位与的方式导入到加密过程中的中间变量中，进而改变了该半字节的分布率.本节以恢复k1的16 b为例，分别考量SEI区分器、GF区分器和GF-SEI双重区分器的故障数和耗费时间，所有数据均为实验1 000次后的平均值.图3表示在不同的区分器作用下恢复出子密钥的概率.其中，横坐标轴表示导入的故障数，纵坐标轴表示恢复出正确子密钥的成功率.3种不同线段分别表示使用SEI区分器、GF区分器和GF-SEI双重混合区分器进行统计分析的结果.实验结果表明，在半字节随机故障模型下，使用SEI区分器、GF区分器和GF-SEI双重区分器时，分别需要68,64和48个故障，即可以99%的概率恢复出步骤3中的子密钥.因而使用后2种区分器可以降低攻击所用故障数，并且使用GF-SEI双重区分器时故障数减少明显.

图4表示使用SEI区分器、GF区分器和GF-SEI双重混合区分器破译密钥的时间堆积图.其中横坐标轴表示故障导入的个数，纵坐标轴表示以秒为单位的耗时.实验结果表明，在半字节随机故障模型下，3种区分器分别需要2.5 s,2.4 s和1.7 s，即可以99%的概率恢复出步骤3中的子密钥.观察图4可知，对于同一个故障数，使用3种区分器进行统计分析所花费的时间比较接近.特别值得一提的是，使用GF-SEI双重混合区分器不会增加攻击时间.

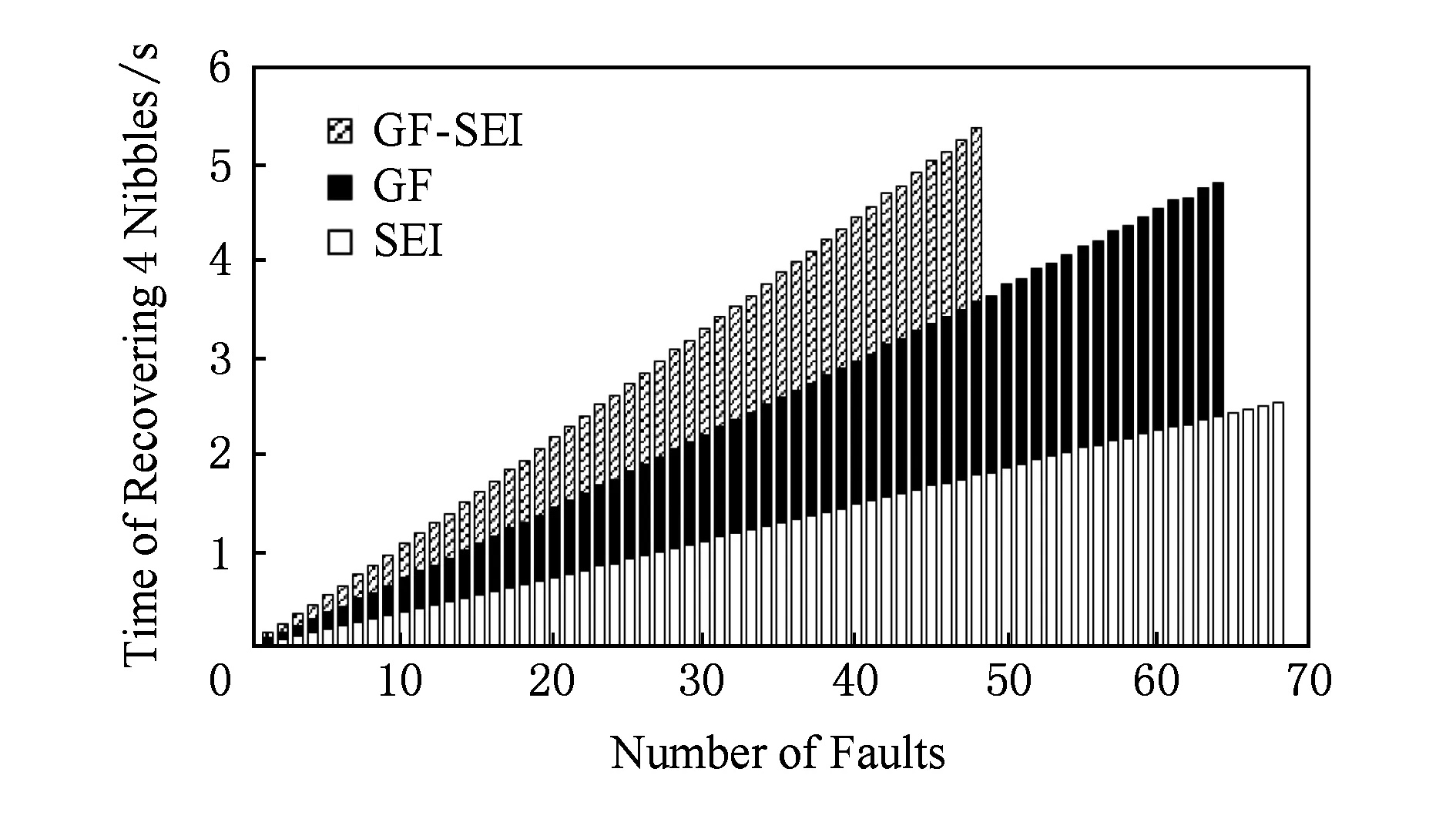
Fig. 4 The time shown with stacked charts of using different faults图4 使用不同故障数时耗费时间的堆积柱形图

结合图3和图4的实验结果， 我们进一步对SEI区分器、GF区分器和GF-SEI双重区分器的破译情况进行了比较，表5为统计故障分析AES算法和LED算法的攻击结果对比.结果表明，使用GF区分器后的攻击效果比SEI区分器的攻击效果略佳，但效果不明显;而使用GF-SEI双重区分器所需要的故障数和耗费的时间比前两者均明显减少，是统计故障分析中目前已知的最佳区分器.

Table5ComparisonofStatisticalFaultAttacksonaPartialSubkeyofAESandLED

表5AES和LED算法统计故障分析部分子密钥结果对比

CipherDistinguisherFaultNumberLatencyTime∕sReferencesAESSEI80Ref[24]SEI682．5LEDGF642．4ThisPaperGF⁃SEI481．7

5 结束语

本文提出了针对LED轻量级密码算法的新型统计故障分析方法.在半字节随机故障模型下，不仅将Fuhr等人的统计故障攻击思想应用于轻量级分组密码算法LED的安全性分析中，而且构建了GF区分器和GF-SEI双重区分器，通过3种区分器均可以恢复原始密钥.相较于原有的SEI区分器，新型区分器从攻击效果和耗费时间上均具有较大优势.结果表明：以LED为代表的轻量级密码算法易受到统计故障分析的威胁，在物联网环境实现时必须加以防护措施进行保护.

[1] Medaglia C M, Serbanati A. An overview of privacy and security issues in the Internet of things[C] //Proc of the Internet of Things. Berlin: Springer, 2010: 389-395

[2] Mayer C P. Security and privacy challenges in the Internet of things[J]. Electronic Communications of the Easst, 2009, 17(3): 11-22

[3] Ning Huangsheng, Liu Hong, Yang L T. Cyberentity security in the Internet of things[J]. Computer, 2013, 46(4): 46-53

[4] Suo Hui, Wan Jiefu, Zou Caifeng, et al. Security in the Internet of things: A review[C] //Proc of the 1st Int Conf on Computer Science and Electronics Engineering. Piscataway, NJ: IEEE, 2012: 648-651

[5] Guo J, Peyrin T, Poschmann A, et al. The LED block cipher[C] //Proc of the 13th Int Workshop on Cryptographic Hardware and Embedded Systems. Berlin: Springer, 2011: 326-341

[6] Ueno R, Homma N, Aoki T. Efficient DFA on SPN-based block ciphers and its application to the LED block cipher[J]. IEICE Trans on Fundamentals of Electronics Communica-tions & Computer Sciences, 2015, 98(1): 182-191

[7] Liu Feng, Liu Xuan, Meng Shuai. Differential fault attack and meet-in-the-middle attack on block cipher LED[J]. Advanced Materials Research, 2013, 850(1): 529-532

[8] Shanmugam D, Selvam R, Annadurai S. Differential power analysis attack on SIMON and LED block ciphers[C] //Proc of the 4th Int Conf on Security, Privacy, and Applied Cryptography Engineering. Berlin: Springer, 2014: 110-125

[9] Isa H, Z’Aba M R. Randomness analysis on LED block ciphers[C] //Proc of the 5th Int Conf on Security of Information and Networks. New York: ACM, 2012: 60-66

[10] Fujishiro M, Yanagisawa M, Togawa N. Scan-based attack on the LED block cipher using scan signatures[C] //Proc of the 20th IEEE Int Symp on Circuits and Systems. Piscataway, NJ: IEEE, 2014: 1460-1463

[11] Isobe T, Shibutani K. Security analysis of the lightweight block ciphers XTEA, LED and Piccolo[C] //Proc of the 17th Australasian Conf on Information Security and Privacy. Berlin: Springer, 2012: 71-86

[13] Soleimany H. Probabilistic slide cryptanalysis and its applications to LED -64 and Zorro[C] //Proc of the 21st Int Workshop on Fast Software Encryption. Berlin: Springer, 2014: 373-389

[14] Boneh D, Demillo R A, Lipton R J. On the importance of checking cryptographic protocols for faults[C] //Proc of the 16th Annual Int Conf on Theory and Application of Cryptographic Techniques. Berlin: Springer, 1997: 37-51

[15] Boneh D, Lipton R J. On the importance of eliminating errors in cryptographic computations[J]. Journal of Cryptology, 2001, 14(2): 101-119

[16] Mendel F, Rijmen V, Toz D, et al. Differential analysis of the LED block cipher[C] //Proc of the 18th Int Conf on the Theory and Application of Cryptology and Information Security. Berlin: Springer, 2012: 190-207

[17] Jeong K, Lee C. Differential fault analysis on block cipher LED -64[G] //Future Information Technology, Application, and Service. Berlin: Springer, 2012: 26-34

[18] Li Wei, Gu Dawu, Xia Xiaoling, et al. Single byte differential fault analysis on the LED lightweight cipher in the wireless sensor network[J]. International Journal of Computational Intelligence Systems, 2012, 5(5): 896-904

[19] Li Wei, Gu Dawu, Zhao Chen, et al. Security analysis of the LED lightweight cipher in the Internet of things[J]. Chinese Journal of Computers, 2012, 35(3): 434-445

(李玮, 谷大武, 赵辰, 等. 物联网环境下LED轻量级密码算法的安全性分析[J]. 计算机学报, 2012, 35(3): 434-445)

[20] Jovanovic P, Kreuzer M, Polian I. A fault attack on the LED block cipher[C] //Proc of the 3rd Int Conf on Constructive Side-Channel Analysis and Secure Design. Berlin: Springer, 2012: 120-134

[21] Zhao Xinjie, Guo Shize, Zhang Fan, et al. Improving and evaluating differential fault analysis on LED with algebraic techniques[C] //Proc of the 8th Workshop on Fault Diagnosis and Tolerance in Cryptography. Piscataway, NJ: IEEE, 2013: 41-51

[22] Ji Keke, Wang Tao, Zhao Xinjie, et al. Algebraic fault attack on LED light-weight block cipher[J]. Application Research of Computers, 2013, 30(4): 1183-1186

(冀可可, 王韬, 赵新杰, 等. 轻型分组密码LED代数故障攻击方法[J]. 计算机应用研究, 2013, 30(4): 1183-1186)

[23] Li Wei, Zhang Wenwen, Gu Dawu, et al. Impossible differential fault analysis on the LED lightweight cryptosystem in the vehicular ad-hoc networks[J]. IEEE Trans on Dependable & Secure Computing, 2016, 13(1): 84-92

[24] Fuhr T, Jaulmes E, Lomne V, et al. Fault attacks on AES with faulty ciphertexts only[C] //Proc of the 8th Workshop on Fault Diagnosis and Tolerance in Cryptography. Piscataway, NJ: IEEE, 2013: 108-118

ResearchontheLEDLightweightCipherAgainsttheStatisticalFaultAnalysisinInternetofThings

Li Wei1,2,3, Ge Chenyu1, Gu Dawu2, Liao Linfeng1, Gao Zhiyong1, Guo Zheng4, Liu Ya5, Liu Zhiqiang2, and Shi Xiujin1

1(SchoolofComputerScienceandTechnology,DonghuaUniversity,Shanghai201620)2(DepartmentofComputerScienceandEngineering,ShanghaiJiaoTongUniversity,Shanghai200240)3(ShanghaiKeyLaboratoryofIntegrateAdministrationTechnologiesforInformationSecurity(ShanghaiJiaoTongUniversity),Shanghai200240)4(SchoolofMicroelectronics,ShanghaiJiaoTongUniversity,Shanghai200240)5(DepartmentofComputerScienceandEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093)

The typical lightweight cipher LED, proposed in CHES 2011, is applied in the Internet of things (IoT) to provide security for RFID tags and smart cards etc. Fault analysis has become an important method of cryptanalysis to evaluate the security of lightweight ciphers, depending on its fast speed, simple implementation, complex defense, etc. On the basis of the half byte-oriented fault model, we propose new statistical fault analysis on the LED cipher by inducing faults. Simulating experiment shows that our attack can recover its 64-bit and 128-bit secret keys with 99% probability using an SEI distinguisher, a GF distinguisher and a GF-SEI distinguisher, respectively. The attack can be implemented in the ciphertext-only attacking environment to improve the attacking efficiency and decrease the number of faults. It provides vital reference for security analysis of other lightweight ciphers in the Internet of things.

Internet of things (IoT); lightweight cipher; LED; statistical fault analysis; cryptanalysis

TP309.7

LiWei, born in 1980. PhD, associate professor. Senior member of CCF. Her main research interests include the design and analysis of symmetric ciphers.

GeChenyu, born in 1992. Master candidate. Her main research interests include security analysis of lightweight ciphers.

GuDawu, born in 1970. PhD, professor and PhD supervisor. Senior member of CCF. His main research interests include cryptology and computer security.

LiaoLinfeng, born in 1993. Master candidate. His main research interests include security analysis of symmetric ciphers.

GaoZhiyong, born in 1992. Master candidate. His main research interests include security analysis of symmetric ciphers.

GuoZheng, born in 1980. PhD, lecturer. His main research interests include the design and analysis of smart cards and chips.

LiuYa, born in 1983. PhD, lecturer. Her main research interests include the design and analysis of symmetric ciphers and computational number theory.

LiuZhiqiang, born in 1977. PhD, associate professor. His main research interests include block chain, DAG -based distributed system, cryptanalysis and design of block ciphers and Hash functions.

ShiXiujin, born in 1975. PhD, associate professor. His main research interests include security analysis of the Internet of things.

附录A. 实验数据及结果.

以LED -64算法为例.

明文：随机生成；

密钥：01 23 45 67 89 AB CD EF.

实验结果表明：通过3种区分器均可以恢复原始密钥，具体数据如表A1和表A2所示:

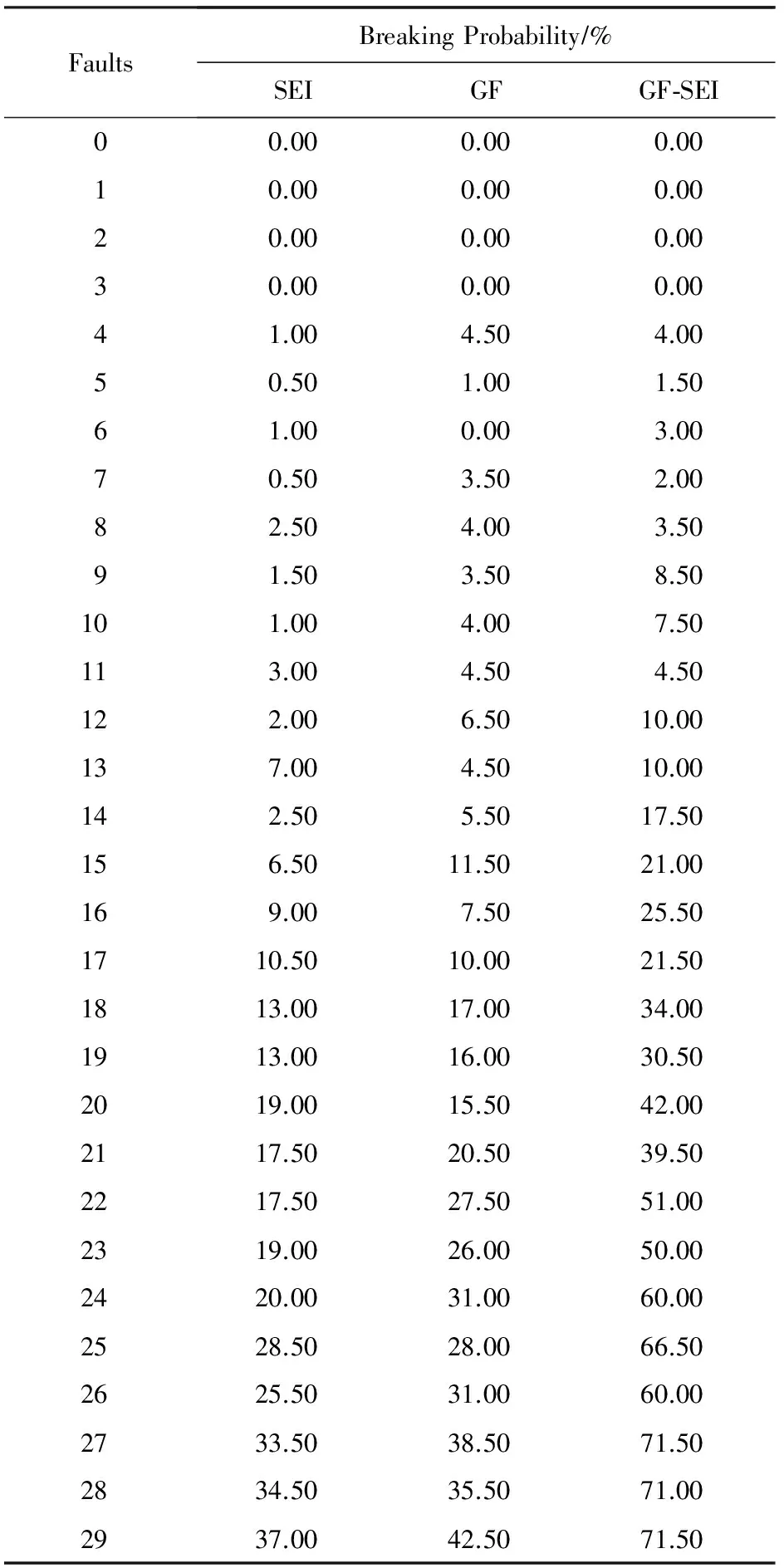
Table A1 Probability of Breaking LED Using Different Distinguishers

Continued (Table A1)

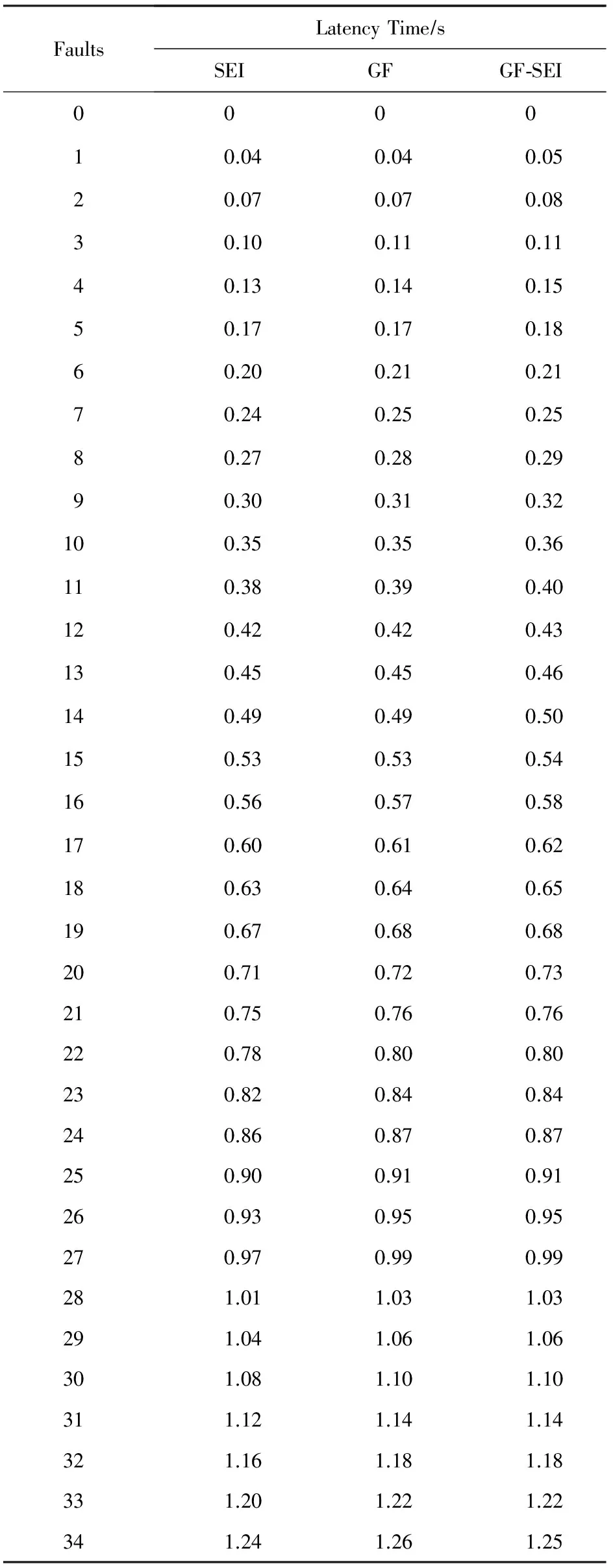
Table A2 Time of Breaking LED Using Different Distinguishers

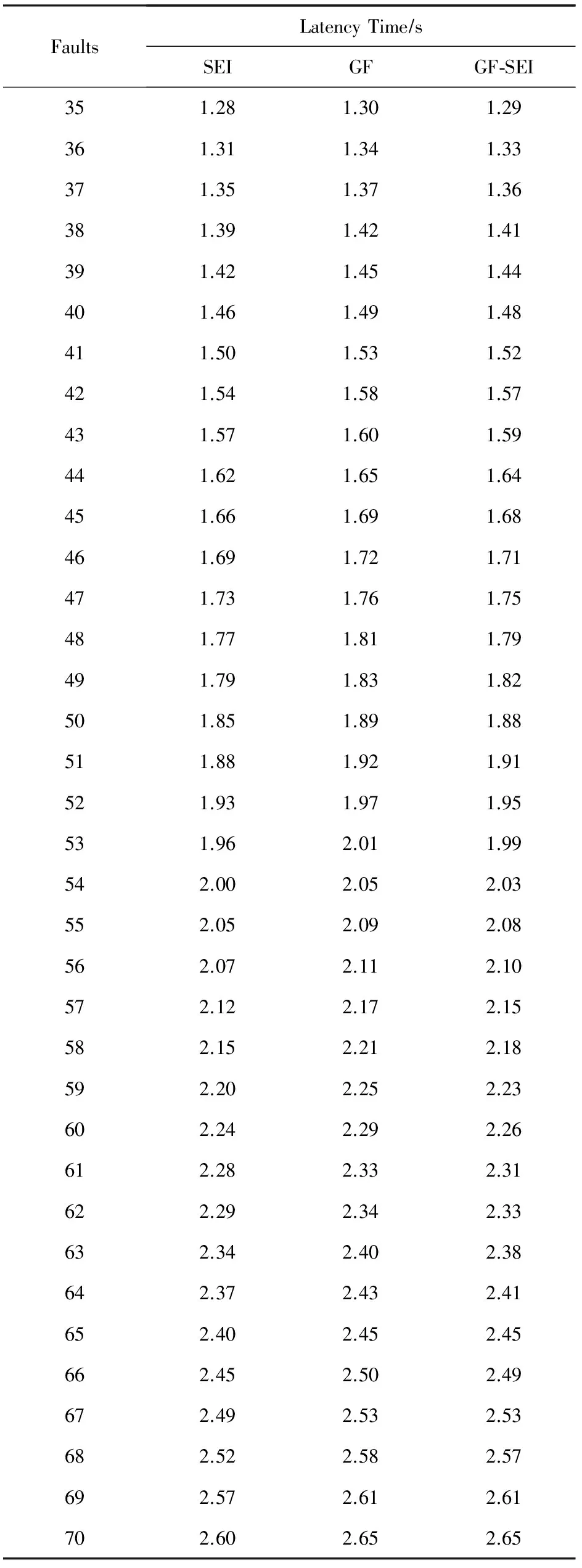
Continued (Table A2)