高精度测距验证系统的设计与实现

叶 蓓，王春晖，张朝杰，金仲和

(浙江大学微小卫星研究中心，杭州 310027)

高精度测距验证系统的设计与实现

叶 蓓，王春晖，张朝杰，金仲和

(浙江大学微小卫星研究中心，杭州 310027)

针对星间高精度测距系统地面远距离验证困难的问题，提出一种新的地面验证系统。该系统利用100 km光纤模拟地面长距离，通过测量载波相位波动并反馈控制光延时线的延时量，使光纤与光延时线总的传输延时保持稳定。本文对系统的相位传递关系及系统中存在的主要噪声进行理论分析并建立相应的模型，通过仿真和试验验证系统能够达到的精度。仿真及试验结果均表明，该系统能够抑制光纤传输延时的低频漂移，其精度能够满足高精度测距系统地面远距离验证的要求。

高精度测距；地面验证；远距离；延时漂移

0 引 言

星间高精度测距系统能够用于卫星之间相对距离的精确测量，这使得它在卫星编队、组网和地球重力场模型恢复方面具有重要的作用[1-4]。通常，在实际应用之前测距系统需要进行地面远距离的验证，以降低相关项目开发的风险。然而，目前还没有一种有效的用于远距离验证高精度测距系统精度的方法。研制这种地面远距离验证系统主要存在两个困难：1)实际应用的星间测距系统精度很高，目前难以用其他的测距系统作为参考。2)缺少合适的传输媒介，若以空气作为传输媒介，当距离相隔数十千米时，很难选出合适的测试地点，且会存在多径干扰问题，而射频线缆体积大，衰减大，也不适合用作传输媒介。文献[5]提出用光纤模拟长距离，光纤本身具有抗干扰能力强、体积小、衰减小的特点，克服了空气和射频电缆的缺陷。传输信号对光载波进行强度调制后在光链路中传输，传输延时的大小会反映到该传输信号的相位中，在光链路的末端光电检测器检测出该电信号，进而通过测量相位变化解算出传输时延的变化。传输信号在无线链路和光纤中的传输时延最终都反映到了传输信号的相位变化上，因此能够用光纤模拟真实太空环境中的星间链路。但光纤的传输延时会受到温度和光纤链路上分布应力等因素的影响而波动，对于长距离光纤，由温度变化引起的距离测量值漂移远大于测距系统的精度。若将光纤用于长距离的测距精度验证，必须采取一定的措施抑制光纤的延时变化，使其延时变化的稳定度达到亚皮秒量级。

时频传输领域中已有一些文献阐述了利用光延时线或电延时器、相位共轭器来稳定光纤传输延时的方法[6-12]，其目的是将标准时频信号不失真地进行传输。本文将光延时线扩展应用到测距验证系统中，与时频信号传输不同的是，测距验证系统的目的是提供一段稳定的传输媒介作为衡量其他测距系统的标尺。该系统通过测量载波信号相位波动进而反馈控制光延时线的延时，抑制了光链路传输延时的漂移。同时，该测距验证系统的测量信号与参考信号由同一时钟频率源驱动产生，系统中两者做差比较，能够消除时钟频率源中长期噪声的影响，进一步提高了测距验证系统的精度[13]。本文通过对系统及系统中的主要噪声进行理论分析及建模，仿真分析了系统能够达到的精度，最后通过试验加以验证。仿真及试验结果均表明，该系统能够抑制光链路传输延时的低频漂移，且系统精度能够满足高精度测距系统地面远距离测距验证的要求。

1 系统简介

图1为高精度测距验证系统的系统框图。该系统用高稳石英频标作为整个系统的频率源，其输出的10 MHz信号作为参考信号输入频率综合器1中，产生2250 MHz的射频信号。激光器产生光波长为1550 nm的光信号。电光调制器将频率综合器1输出的射频信号与待验证的测距系统信号调制到光链路上。光信号通过100 km光纤及光延时线，掺铒光纤放大器使光信号到达光电探测器输入端时保持足够的信号功率，光电检测器解调出调制在光信号上的电信号。频率综合器2产生另外一路射频信号，频率为2180 MHz，参考信号同样由高稳石英频标提供。分路器和滤波器将测距系统信号分离出来，分路器的另一路输出信号与2180 MHz信号在混频器中进行混频，生成的70 MHz中频信号经数模转换后输入相位测量模块。测量得到的信号相位与一个参考相位值比较得到相位差。该相位差信号输入PI控制器，输出的控制信号反馈控制光延时线的延时量，最终使光纤与光延时线总的传输延时保持稳定。相位测量及光延时线反馈控制功能均由现场可编程门阵列(Field programmable gate array,FPGA)完成。

2 系统建模

2.1系统相位传递模型

高稳石英频标输出信号相位表示为

φ0(t)=ω0t+φ0

(1)

式中：ω0为高稳石英频标的标称角频率，φ0为初相。

光电探测器输出信号相位为

φ1(t)= 225ω0(t-τfiber(t)-τODL(t))+

225φ0+φd

(2)

式中：τfiber(t)，τODL(t)分别为光纤、光延时线的传输延时，φd为光电调制器、光电探测器及掺铒光纤放大器引入的固定相位偏差。

同时频率综合器2输出信号相位为

φ2(t)=218ω0t+218φ0

(3)

由此得到混频器输出的中频信号相位为

φ3(t)= 7ω0t+7φ0-225ω0(τfiber(t)+

τODL(t))+φd

(4)

中频信号经模数转换器(Analog-to-digital converter,ADC)采样后进行数字正交下混频处理，得到基带信号，基带信号的相位表示为

φ4(t)= 7φ0-225ω0(τfiber(t)+τODL(t))+

φd+φm

(5)

式中：φm表示正交下混频引入的固定相位偏差。

全数字锁相环跟踪基带信号的相位变化，其环路传递函数为H(s)，其输出的相位信号为φout(t)，得到

(6)

式中：φc=7φ0+φd+φm，φout(s)，τfiber(s)，τODL(s)分别是φout(t)，τfiber(t)，τODL(t)的拉氏变换。

理想情况下，光延时线引入的延时变化能够抵消环境变化引起的光纤传输延时变化，输出相位φout(t)为一个固定的常数φref。参考相位φref与输出相位φout(t)作差得到误差信号，输入到传递函数为F(s)的PI控制器，得到光延时线的控制信号，调整光延时线的延时量，即

(7)

将式(6)代入式(7)，得到

(8)

式中：等号右边第1项是由系统引入的固定延时补偿量，第2项是由光纤延时变化引入的补偿量，此补偿量随光纤延时变化而相应变化。

将式(7)代入式(6)，得到

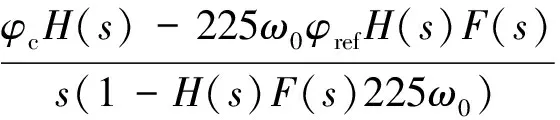
(9)

当忽略常数项影响时，可以得到φout(s)关于光纤延时τfiber(s)的传递函数

(10)

根据系统相位传递模型的推导，得到简化的系统模型框图(见图2)。该系统是嵌套环结构，内部的小环是全数字锁相环，用于捕获并跟踪输入信号的相位，外部的大环是延时反馈环路，用于反馈控制光延时线的延时量。

实际系统中采用电动可调光延时线，其原理是用机械马达调整光通量中的空气间隙的长度，可调范围为600 ps，分辨率为0.05 ps。该款光延时线具有30种不同的执行速度。光延时线依靠机械马达来改变光程，每次调整要消耗一定的时间，包括指令发送时间、马达执行时间、执行完毕所需的稳定时间。因此光延时线的PI控制器工作频率最大不会超过10 Hz。

2.2系统稳定性分析

全数字锁相环的传递函数为

(11)

式中：Kp1、Ki1是全数字锁相环中环路滤波器的参数。

延时反馈环路中PI控制器的传递函数为

(12)

式中：Kp2、Ki2是PI控制器的参数。

将式(11)、式(12)代入式(10)，整理得到

(13)

式中：G=225ω0。

其特征方程式为

s3+ (Kp1-GKp1Kp2)s2+

(Ki1-GKp1Ki 2-GKp2Ki1)s-GKi1Ki2=0

(14)

根据劳斯稳定判据[14]，为使图2中嵌套环内的全数字锁相环保持稳定，Kp1、Ki1需大于0，若要使整个嵌套环保持稳定状态，参数Kp2、Ki2的选择还需要满足以下条件：

或

(15)

工程上常取锁相环的阻尼系数为0.707，这里将全数字锁相环环路的等效噪声带宽设置为1 Hz，得到Kp1、Ki1的值分别为13.33、18.86。将Kp1、Ki1的值代入式(15)，可以得到整个系统处于稳定状态时PI控制器系数Kp2、Ki2的取值范围。

3 系统噪声分析

该测距验证系统中，影响测距值精度的除了光纤引入的相位噪声以外，其他噪声主要还包括：时钟频率源噪声、频率合成器噪声。下面将对这些噪声进行分析。

3.1光纤引入的相位噪声

光纤引入的相位噪声主要来自于由温度和机械应力变化引起的光纤长度的变化，长度变化影响光链路的传输延时，从而导致光纤中传输信号的相位出现随机抖动。光纤互联点处的内反射、受激布里渊散射、偏振模色散波动等其他噪声都来自于机械应力的扰动[15]。

温度变化是一个比较缓慢的过程，它对光纤的影响主要体现在长期稳定性。机械应力对光纤的影响主要表现为短期稳定性的变化[12]。在实验室环境下，光纤链路的特点是：光纤裸露，对环境温度变化的响应快，在空调打开的情况下，室内温度变化范围不会太大；振动较少，短期稳定性相对比较好。

当系统开环工作时，即光延时线不对光链路传输延时进行补偿，系统输出相位φout(t)中包含了光纤引入的相位噪声以及其他噪声源的影响。由于目前不具备单独测量光纤延时变化的设备，这里我们对比了不接入光纤、接入100 km光纤两种情况下开环系统输出信号相位φout(t)的阿伦方差，如图3所示。

由图3可知，当平均时间小于40 s，两种情况下的阿伦方差几乎一致，说明接入光链路并没有显著影响输出结果的高频噪声。当平均时间大于40 s，接入100 km光纤的曲线逐渐偏移不接入光纤的曲线，此时100 km光纤引入的低频噪声占主体。假设光纤仅引入低频的相位噪声，对接入100 km光纤的开环系统输出相位进行平滑滤波，滤除高频噪声的同时保留相位的低频漂移趋势。平滑函数采用MATLAB提供的smooth函数。滤波后的相位值作为光纤传输延时的相位漂移模型。

3.2时钟频率源噪声

时钟的相位噪声是各种因素相互作用的复杂结果，影响因素可以从原子组成到物理环境变化。频率源的频率稳定度可以从时域阿伦方差和频域相对频偏的谱密度两个方面来描述和测量[16]。

由于系统中使用的高稳石英频标的性能优于普通相噪仪频率源的性能，无法用普通相噪仪测量高稳石英频标的相位噪声。器件手册上列出了频偏为1 Hz，10 Hz，100 Hz，1 kHz，10 kHz，100 kHz时的相位噪声功率谱密度值，将这几个点的值在MATLAB中进行插值运算，得到插值后的相位噪声功率谱密度曲线如图4所示。插值后的数据作为时钟频率源噪声的仿真模型。

3.3频率综合器噪声

该系统中运用了集成的频率综合器芯片完成倍频功能，因此必须考虑频率综合器的内部噪声。芯片内部的各个噪声源通过锁相环环路的传递后，都将转变成频率综合器输出端的噪声信号。下面根据文献[17-18]提出的噪声仿真分析方法，建立系统中的频率综合器噪声仿真模型。频率综合器内部的噪声源主要包括：

1)鉴相器噪声。频率综合器芯片属于电荷泵锁相环(Phase locked loop,PLL)，其噪声与鉴相频率有关。鉴相器引入的噪声功率谱密度为

Npd(f)=Npd_ref+10lg(fcomp)

(16)

式中：Npd_ref是鉴相器基底噪声，fcomp为鉴相频率。

2)环路滤波器的电阻热噪声。实际采用的3阶环路滤波器结构如图5所示。由于采用了无源滤波器作为环路滤波器，因此需要考虑电阻热噪声。这个噪声是白噪声，噪声功率表示为

Pr_noise=4K·T·B·R

(17)

式中：K为普朗克常数，T为温度，B为带宽，R为电阻值。大多数情况下，采用1 Hz的带宽。

3)压控振荡器(Voltage controlled oscillator,VCO)相位噪声。VCO的相位噪声功率与距离载波的频偏成反比，大多数情况下可以用1/f噪声来近似[19]

Nvco(f)=Nvco_ref-20lg(f/fref)

(18)

式中：fref是参考频率，Nvco_ref是在参考频率点的相位噪声大小。

各个噪声按照传递函数作用在频率综合器的输出端，不同噪声源对频率综合器输出端的传递函数在很多关于锁相环的文献中均有论述，这里不再赘述。实际系统中使用的频率综合器芯片为ADF4360-2，噪声本底Npd_ref是-216 dBc/Hz，鉴相频率fcomp为100 kHz；鉴相器增益Kp为5 mA；VCO在100 kHz频偏处的噪声是-110 dBc/Hz，VCO灵敏度为57 MHz/V。图5中环路滤波器的元件C1的值为180 pF，C2为2.2 nF，C3为82 pF，R2为8.2 kΩ，R3为16 kΩ。频率综合器1的R分频器系数RPLL1为100，N分频器系数NPLL1为22500，频率综合器2的R分频器系数RPLL2为100，N分频器系数NPLL2为21800。以频率综合器1为例，画出频率综合器的噪声功率谱密度曲线如图6所示。

4 系统仿真

输入到频率综合器的时钟频率源噪声按照环路传递函数同样作用于频率综合器的输出端。以频率综合器1为例，最后到达VCO输出端的时钟频率源噪声为

(19)

式中：Suso(f)是时钟频率源的相位噪声谱密度。

用SPLL1(f)、SPLL2(f)分别表示频率综合器1、频率综合器2的相位噪声谱密度，Suso_pll2(f)表示到达频率综合器2的VCO输出端的时钟频率源噪声。分别将SPLL1(f)、SPLL2(f)、Suso_pll1(f)、Suso_pll2(f)开平方并做反快速傅里叶变换(Inverse fast Fourier transform,IFFT)后，得到相应的相位噪声序列，同光纤传输延时的相位漂移模型一起输入到系统的仿真模型中。第2.1节提到由于光延时线工作频率的限制，其PI控制器工作频率较低，最大不超过10 Hz。系统的Simulink仿真模型是根据图2的简化系统模型搭建的z域模型，考虑到PI控制器控制频率的限制，需要在PI控制器的前一级加一个零阶保持器，以改变PI控制器的工作频率。系统的仿真结果如图7所示。

为了得到系统的性能和PI控制器控制频率的关系，分别仿真PI控制器的工作频率为1 Hz、10 Hz和100 Hz时系统能够达到的性能。仿真结果如表1所示。相位值与测距值转换关系为

(20)

式中：ρ是测距值，c是真空中的光速，f是光纤中传输的射频信号的频率，f=2250 MHz，φout(t)是系统输出相位值。

表1 系统在不同控制频率下能够达到的最佳性能Table 1 Optimal performance under different control frequency

图7的仿真结果表明，测距验证系统能够较好地抑制光链路传输延时的低频漂移，使光链路的传输延时保持稳定。同时从表1的仿真结果可以看出，PI控制器的工作频率越高，系统能够达到的精度越高。由此可以推断系统精度可能受限于光延时线的工作频率。由于光纤传输延时变化的频率较低，光延时线能够对其进行补偿，系统中存在的高频噪声影响了系统能够达到的精度。

5 试验校验

实际的测距验证系统如图8所示。图中标示出了石英频标、光纤、电光调制器、光电探测器和光延时线；图中未标出的器件如频率合成器、混频器均集成在电路板上，相位测量模块、延时反馈模块均在现场可编程门阵列FPGA。

根据前面的仿真结果，实际系统中的光延时线工作频率设置为10 Hz。实测测距值曲线如图9所示。在测距值曲线的前半段，曲线近似为一条水平的直线，此时系统为闭环状态，系统能够补偿光纤传输延时造成的测试输出结果的漂移。当断开对光延时线的控制后(见图中开环点)，输出结果发生漂移。图10为系统闭环工作时，输出结果的局部放大波形。系统闭环工作时，计算得到系统实测精度能够达到92.2 μm。试验结果与仿真结果基本吻合。

6 结 论

针对高精度测距系统地面远距离验证困难的问题，本文提出了一种新的验证方法。该方法用100 km的光纤模拟空间远距离，光纤容易受外界温度、振动等因素的影响，导致传输延时发生漂移，造成验证系统的系统误差超过了测距系统的精度。本文将光延时线作为可控延时单元扩展应用到该验证系统中，设计了延时反馈环路，仿真及试验验证该方法能够显著抑制光链路的低频漂移，使光纤与光延时线的总传输延时保持稳定。本文介绍了系统结构，详细分析了系统的相位传递模型和系统的稳定性条件以及系统中存在的影响测距精度的其他噪声，并在Simulink中进行了仿真分析。考虑到PI控制器控制速率的影响，分别仿真了不同PI控制器控制速率条件下的系统性能。结果表明，控制速率越高，系统能够达到的精度越高，仿真得到的系统精度为70.3 μm。最后在实际搭建的系统上进行试验验证，实际测量得到系统的精度是92.2 μm，能够满足高精度测距系统的远距离地面验证要求。

[1] 刘洋, 易东云, 王正明. 编队卫星星间基线的高精度测量方法研究[J]. 宇航学报, 2007, 28(6): 1643-1647. [Liu Yang, Yi Dong-yun, Wang Zheng-ming. Research on high precision measure methods of inter-satellite baselines of formation flying satellites[J]. Journal of Astronautics, 2007, 28(6): 1643-1647.]

[2] 王世练, 路军, 张尔扬. 基于星间无线电测距的卫星自主定轨与导航[J]. 宇航学报, 2002, 23(1): 69-72. [Wang Shi-lian, Lu Jun, Zhang Er-yang. Satellite autonomous orbit determination and navigation based on wireless distance measurement on-board[J]. Journal of Astronautics, 2002, 23(1): 69-72.]

[3] 佘世刚, 王锴, 周毅,等. 高精度星间微波测距技术[J]. 宇航学报, 2006, 27(3):402-406. [She Shi-gang, Wang Kai, Zhou Yi, et al. The technology of high accuracy inter-satellite microwave ranging[J]. Journal of Astronautics, 2006, 27(3): 402-406.]

[4] Jilla C D, Miller D W. Multi-objective, multidisciplinary design optimization methodology for distributed satellite systems[J]. Journal of Spacecraft and Rockets, 2004, 41(1): 39-50.

[5] 郭学卫. 星间高精度测距系统的精度验证及精度优化[D]. 杭州： 浙江大学, 2013. [Guo Xue-wei. The verification and optimization for the accuracy of high-precision ranging system between satellites[D]. Hangzhou: Zhejiang University, 2013.]

[6] Lopez O, Amy-Klein A, Daussy C, et al. 86 km optical link with a resolution of 2×10-18for RF frequency transfer[J]. European Physical Journal D, 2008, 48(1): 35-41.

[7] Kiuchi H. Highly stable millimeter-wave signal distribution with an optical round-trip phase stabilizer[J]. IEEE Transactions on Microwave Theory & Techniques, 2008, 56(6): 1493-1500.

[8] Celano T P, Stein S R, Gifford G A, et al. Sub-picosecond active timing control over fiber optic cable[C]. The 2002 IEEE International Frequency Control Symposium & PDA exhibition, New Orleans, USA, May 29-31, 2002.

[9] Wang X, Liu Z, Wang S, et al. Photonic radio-frequency dissemination via optical fiber with high-phase stability [J]. Optics Letters, 2015, 40(11): 2618-2621.

[10] Wang B, Gao C, Chen W L, et al. Precise and continuous time and frequency synchronisation at the 5×10-19accuracy level[J]. Scientific Reports, 2012, 2: 556.

[11] Sliwczynski, Krehlik P, Buczek, et al. Active propagation delay stabilization for fiber-optic frequency distribution using controlled electronic delay lines[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(4): 1480-1488.

[12] Narbonneau F, Lours M, Bize S, et al. High resolution frequency standard dissemination via optical fiber metropolitan network [J]. Review of Scientific Instruments, 2006, 77(6).

[13] Zhao M C, Wang C H, Jin Z H. Design and derivation of the dual transponder carrier ranging system[J]. Journal of Zhengjiang University-SCIENCE C (Computer & Electronics), 2013, 14(5): 383-394.

[14] 邹伯敏.自动控制理论[M].北京：机械工业出版社,2007：83.

[15] Foreman S M, Holman K W, Hudson D D, et al. Remote transfer of ultrastable frequency references via fiber networks[J]. Review of Scientific Instruments, 2007, 78(2).

[16] 王宏汤. 用自相关系数法分析精密频率源的噪声模型[J]. 宇航学报, 1981, 2(2):34-44. [Wang Hong-tang. An autocorrelation coefficient method for analysing the mode of noise in precise frequency sources[J]. Journal of Astronautics, 1981, 2(2): 34-44.]

[17] 王春晖, 郁发新, 金仲和,等. 皮卫星星载测控应答机的噪声研究[J]. 系统工程与电子技术, 2007, 29(9): 1514-1517. [Wang Chun-hui, Yu Fa-xin, Jin Zhong-he, et al. Research on the noise of TT&C transponder for pico-satellites[J]. Systems Engineering and Electronics, 2007, 29(9): 1514-1517.]

[18] 王春晖，金小军，金仲和，等. 锁相环中数字分频器对输出信号相位噪声和杂散的影响[J]. 宇航学报, 2009, 30(6):2334-2338. [Wang Chun-hui, Jin Xiao-jun, Jin Zhong-he, et al. Effect of digital frequency dividers on spurs and PM noise in PLL[J]. Journal of Astronautics, 2009, 30(6): 2334-2338.]

[19] Hajimiri A, Lee T H. A general theory of phase noise in electrical oscillators[J]. IEEE Journal of Solid-State Circuit, 1998, 33 (2): 179-194.

DesignandImplementationofHigh-PrecisionRangingValidationSystem

YE Bei, WANG Chun-hui, ZHANG Chao-jie, JIN Zhong-he

(Micro-Satellite Research Center, Zhejiang University, Hangzhou 310027, China)

A new method of long-distance ground-based validation for high-precision inter-satellite ranging system is proposed. A piece of optical fiber with a length of 100 km is used as the long-distance signal path. The drift of the optical fiber transmission delay is suppressed substantially by measuring the carrier phase and then feedback controlling the optical delay line. In this way, the total transmission delay of the optical path remains stable. The phase transfer relationship of the system and the main noise in the system are analyzed meanwhile the corresponding models are established in this paper. Simulation and system experiments are performed to demonstrate that the actual accuracy meets the requirements of the system which can be used in the long-distance validation of a high-precision ranging system.

High-precision ranging; Ground-based validation; Long-distance; Delay drift

V566

A

1000-1328(2017)10- 1097- 08

10.3873/j.issn.1000-1328.2017.10.010

2017- 05- 05;

2017- 08- 23

国家自然科学基金(61401389)

叶蓓(1992-)，女，博士生，主要从事星间高精度测距系统研究。

通信地址：浙江省杭州市浙江大学玉泉校区智泉大楼C402(310027)

电话：13738149357

E-mail: yebei@zju.edu.cn

王春晖(1983-)，男，博士，副教授，主要从事皮卫星测控应答机设计、射频集成通讯系统研究。本文通信作者。

通信地址：浙江省杭州市浙江大学玉泉校区智泉大楼C402(310027)

电话：(0571)87953857

E-mail: hytgwch@zju.edu.cn