高轨失稳目标单载荷相对位姿测量方法

李荣华，李金明，陈 凤，肖余之

(1. 大连交通大学机械工程学院，大连 116028；2. 上海宇航系统工程研究所，上海 201109)

高轨失稳目标单载荷相对位姿测量方法

李荣华1,2，李金明1，陈 凤2，肖余之2

(1. 大连交通大学机械工程学院，大连 116028；2. 上海宇航系统工程研究所，上海 201109)

针对线阵扫描型激光雷达在探测高轨失稳目标过程中，发生时空非定常点云数据畸变，而需多载荷协同方式测量相对位姿问题，提出一种激光雷达同向差分扫描测量方法。该方法基于运动目标畸变点云信息瞬时拓扑结构不变性，首先对相邻两次扫描的畸变点云进行配准来获取目标运动增量、解算目标瞬时运动参数。其次，逐条恢复畸变扫描线点云所处目标真实几何位置、完成目标三维重建。然后以目标三维模型为初始位姿基准，通过设定增量次数阈值不断更新位姿基准实现误差自标定。最后通过叠加位姿增量获取目标相对位姿。该方法在缺失非合作目标先验信息的情况下，仅使用单一载荷，不仅实现了目标三维点云模型的重建，而且精确测量了空间非合作目标相对位姿。

同向差分扫描；畸变恢复；自标定；位姿增量

0 引 言

高轨(GEO)由于大量失稳目标的占用，造成了轨位资源的极大浪费，加之高轨卫星在军民领域作用的日益明显，研究高轨失稳卫星的在轨服务技术已刻不容缓[1-3]。其中，高轨失稳目标相对位姿实时性测量技术是实现在轨服务必须解决的关键点和难点。高轨失稳目标作为空间非合作目标由于不能直接利用星间链路来直接传输其位置和姿态信息，导致目前主要以光学测量手段为主[4]。例如：Sharma等[5]基于单目视觉对飞行器进行了位姿测量，但由于单目相机缺少深度信息，需要假设特征点坐标已知；虽然Li等[6]基于双目相机可以实现卫星太阳能帆板的特征提取与相对位姿测量，但由于双目视觉测量依靠同名点的识别与匹配导致对目标表面纹理特性依赖程度很高，且测量精度受太空光照条件等因素限制而只适用于近距离的交会对接测量[7]；哈尔滨工业大学的梁斌等[8]和上海宇航系统工程研究所的刘玉等[9]分别基于ToF相机对非合作目标位姿测量展开过论述和应用研究，但限于获取的点云分辨率过低，导致点云匹配精度无法满足实际任务需求；冯春等[10]提出利用单目视觉与激光测距仪融合测量航天器间相对位姿参数，但多传感器势必会增加空间载荷；虽然激光雷达工作时也会不可避免的受到太阳辐射及其反射产生的噪声干扰，尤其当太阳光强直射并会聚到光学探测器件上会形成“猫眼效应”[11]，但相比其他光学测量手段，激光成像雷达具有工作距离长、工作频率高、波束窄，距离和角度测量精度高等诸多优势，在空间应用上的需求越来越迫切[12-15]。

激光雷达在单点扫描方式的基础上发展了线阵扫描型和面阵非扫描型成像方式。由于高轨目标体积大，面阵非扫描型激光雷达难以实现高分辨率、大视场角测量；而线阵扫描式激光雷达同一时刻只能获取目标的一组线信息，当高轨目标处于失稳状态时，测量获得的时空非定常分布点云数据必然发生畸变，导致后续测量算法无法展开实际应用。美国斯坦福大学空间机器人实验室Russell等[16]采用一种基于非线性估计算法的非合作目标位姿测量方法，该方法无需解决数据扭曲畸变问题就能实现姿态解算，但算法复杂，对硬件处理速度要求很高。本文采用的激光雷达同向差分扫描方法，相比单双目相机可以不需要尺度因子，而是借助扫描点云的拼接，实现目标三维重建；相比面阵激光雷达，本方案测量视场更大，点云分辨率更高，从而保障了位姿测量精度；此外，本文研究内容依据畸变点云拓扑结构的瞬时不变性，通过叠加运动增量而不完全依赖算法即可获取目标相对位姿，解算效率更高；最后，本文还实现了累计误差自标定，保证了测量值的精确性。

综上所述，本研究以解决高轨道失稳非合作目标实时相对位姿测量为目的，针对线阵扫描式激光雷达测量动态目标发生形貌畸变而无法精确测量目标位姿问题，首次提出以畸变配准畸变为核心的激光雷达同向差分扫描方法。该方案的优势在于在国内尚未掌握大面阵激光雷达技术的背景下，仅使用单一载荷(线阵扫描式激光雷达)且不依赖尺度因子的情况下可以实现对动态非合作目标的三维重建，并为解决高轨失稳目标实时相对位姿测量难题提供一种新的研究思路。

1 雷达同向差分扫描估计目标瞬时运动特性

线阵扫描式激光雷达在一定时间内同一扫描方向上对目标扫描两次，并获得点云数据。通过精确配准预测该时间段内目标的运动特性，从而为目标畸变点云形貌恢复及目标三维重建、相对位姿测量提供基础，见图1。

1.1确定目标与雷达坐标系

目标坐标系以目标重心为坐标原点，目标自旋轴方向为Z轴方向，太阳能帆板方向为Y轴方向，并基于右手法则，确定X轴。因为在激光雷达扫描过程中，目标卫星在不断运动，导致获取的每一条目标点云线信息并非处在同一时空状态下，故坐标系的建立以初始获取目标反馈信息的时刻为基准。世界坐标系与雷达坐标系重合，建立目标与雷达的笛卡尔坐标系如图2所示。

1.2差分扫描点云畸变规律不变性的证明

由于失稳目标的不断运动，导致激光雷达扫描过程中获取的点云数据发生运动畸变。证明雷达重复扫描获取的点云数据的畸变规律相同，是实现本文相对位姿测量方法的前提。证明运动目标两组点云畸变规律相同，即证明两组点云的几何尺度和形貌相同。

证明过程依次如下：

1)证明畸变点云几何尺度不变

首先，激光雷达相比其他光学测量手段的优势之一在于可以真实还原现实世界场景尺度；其次，虽然激光雷达扫描过程中点云整体发生畸变，但每一个扫描点到旋转轴的距离并未发生变化，从而以旋转轴建立的目标坐标系下的目标点云几何尺度并未改变，如图3所示。

2)证明畸变点云几何形貌不变

证明点云形貌不变即证明点云中任意两点与旋转轴的夹角在两次扫描中相同。一是，同一条扫描线上的点与点之间到旋转轴的夹角在两次扫描中必然相等。二是，任意两条不重合的扫描线之间夹角的证明只需要证明相邻扫描线的情况成立即可：以图3情况为例，扫描方向与目标自转水平分量方向相逆，设雷达相邻扫描线经过测量时间为t0；目标水平方向自旋角速率为ω；目标真实点云中相邻点与旋转轴夹角为γ；则雷达获取的实际点云中点与点之间夹角表达式为：

γl=γ-ωt0

(1)

因为t0和γ只受激光雷达测量指标决定是定值，目标差分扫描时间内匀速自旋，所以γl在两次扫描中不变，如图3所示：空心点代表目标真实点云，实心点代表实际获取点云，此外由于目标的自转，使得雷达实际获取的点云线之间的密度比真实值变大。证毕。

综上，点云虽然发生畸变，但由于瞬时目标运动特性不变，所以在两次的扫描过程中，点云的畸变规律是相同的，基于此实现畸变点云的配准以及后续的三维重建等工作可行。

1.3雷达同向差分扫描

线阵扫描式激光雷达从t1时刻开始第一次扫描，确保目标完全进入扫描视场，花费扫描时间为T1；将所有获取的点云线信息转换到获取初始第一条线点云所在的坐标系；距离第一次扫描结束一段时间(Δt)后，激光雷达沿着第一次相同扫描方向开始组内差分扫描，花费扫描时间为T2；同样将所有该次获取的点云线信息转换到该次扫描初始时刻坐标系。雷达扫描获取目标可测部位畸变数据示意图见图4。

1.4组内畸变点云配准与相对位姿增量解算

1)组内畸变点云配准

点云自动配准的实质是把不同坐标系中测量得到的数据点云借助重合区域进行坐标变换，以得到更加完整的数据模型。本文的畸变点云配准关键是获取两次扫描点云之间的坐标变换参数R(旋转矩阵)和T(平移矩阵)即雷达在进行差分扫描时间内目标的位姿增量。具体步骤如下：①首先对两次扫描中获取的点云按照同样的关键点选取标准提取关键点；②对选择的所有关键点分别计算其特征描述子；③结合特征描述子在两个数据集中的坐标系位置，以二者的特征和位置的相似度为基础，来估算他们的对应关系，初步估计对应点对；④根据雷达数据噪声特点，除去对配准有影响的错误的对应点对；⑤使用刚体变换把第二次获取的差分扫描点云旋转、平移到第一次扫描时目标所在坐标系，使其满足如下目标函数：

(2)

式中：Qi、Pi为3×1矩阵，分别代表两次扫描点云中的点的三维坐标。

2)相对位姿增量解算

空间失稳目标一段时间内发生空间位移和绕自转轴慢旋，所以配准中的旋转矩阵R和位移矩阵T为

(3)

式中：θ为相邻扫描时间内目标自转角度，在获取旋转矩阵R后，不难解算θ值；X、Y、Z分别为空间位移分量。在求解上，为了适应线性点云和奇异点数据，本文采用四元数方法解算。通过对多组相邻畸变点云数据的配准可以获取沿时间延长的多组有限个相邻扫描时间内的相对位姿增量，见图5。

1.5时间微分获取目标瞬时运动特性

1)统计重合区域点云扫描时间

通过配准，识别两次扫描获取的目标相同部位点云区域，并沿水平方向统计该部位雷达扫描线数N；借助已知的雷达扫描速率v(单位时间雷达所能发射回收的雷达线数)，则T=N/v。(以第一次雷达扫描数据为研究对象)。

2)确定目标相对自身运动趋势

通过配准值中各个量的正负，估计目标相对自身前一时刻的运动方向 ，由此为下一步计算时间间隔提供选择条件。

3)计算扫描重合区域时间间隔t

这里假设目标自旋与雷达扫描在水平方向上相逆，其他情况方法类似。雷达差分扫描时间轴如图6所示，目标从t1时刻(已知条件)开始第一次扫描，经过一段时间开始出现重合区域的第一条线，计该时刻为a1(未知待求量)，再经过时间T(上一步获取)到达t2(已知量)时刻，则第一次扫描结束，共历时T1(已知量)；第一次扫描结束后，经过Δt后的t1′时刻(已知量)雷达开始同向差分扫描，直到差分扫描结束；通过以上表述，可以用t1′时刻与a1时刻的差值来表述待求的时间间隔t，即

(4)

4)计算目标瞬时运动特性

为了恢复激光雷达每一条畸变扫描线的真实位置，需要知道雷达在初始扫描时刻到该条扫描线所经过的时间和目标在该段时间内的平均运动速率。由于相邻扫描时间很短，目标天体可以被认为做瞬时匀速运动。经过第1.4节已经获取第二次扫描点云重合区域相对第一次扫描的位姿增量；经过第1.5节也已经获取了扫描该重合区域所经过的时间，由此可以计算目标在二次扫描时间间隔内相对自身坐标系的相对运动速率(运动速率分为平动速率vx、vy、vz和转动速率ωz。其中相对平动速率以第一次扫描初始时刻的目标坐标系为基准，转动速率绕目标坐标系Z轴旋转)，即

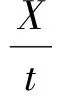
(5)

2 畸变点云线信息恢复与目标三维模型重建

2.1可测部位畸变线信息恢复

以雷达第一次扫描的初始时刻，目标所在空间位置建立目标坐标系，如果想把每一条畸变线信息恢复到目标形貌真实位置(x0,y0,z0)，需要计算该条畸变点云线相对初始时刻所在坐标系的平移量和旋转分量，经过前面的步骤已经获取了目标天体的运动参数模型，可以通过对不同时刻采集的线信息进行逆运算以把多组线信息整合到同一时刻的空间位置，ti代表统计雷达在获取每一条线信息相对初始时刻所经过的扫描时间。则每一条雷达扫描线点云的逆向数据恢复模型为

(6)

其中

(7)

(8)

2.2重建雷达点云三维模型

失稳目标在雷达相邻的两次扫描时间内能够保证有效重合扫描区域，基于此，对目标相邻扫描点云进行拼接；从而在目标旋转周期内，重复扫描、配准过程完成目标表面点云的三维重建。过程如下：

1)获取第j次扫描点云，并作为重建起始，经上一步实现点云畸变信息恢复；

2)获取第j+1次扫描点云，同样恢复畸变信息，与第j次点云进行配准，舍去重合区域；

3)继续获取下一时刻扫描点云，重复上述过程；

4)以当前时刻扫描点云与第j次点云配准重合度作为终止重建条件：当两处点云存在重合区域或者重合度大于设定阈值，认为目标完成一次周期自转，即完成重建工作。

3 增量累计误差自标定与目标相对位姿获取

受激光雷达测量精度、配准算法的截断误差等因素影响，经过一段时间，通过位姿增量叠加来获取的既定时刻相对位姿必然出现误差累计的情况，最终会导致测量值可能严重偏离真值。针对此问题，本方案采用增量累计误差自标定来保证位姿测量精度，如图7所示。

3.1设定增量次数阈值

相对位姿累计误差会随着位姿增量叠加次数的增多而提高，根据技术指标的限定范围和误差源的分析，设定增量叠加次数阈值(M)，实现累计误差最值被限定在技术指标内；而一旦位姿增量次数超出阈值(大于M)，则被认定为测量精度不满足技术指标，从而通过与CAD模型配准重新标定该时刻相对位姿。

3.2匹配三维CAD模型

采用正态分布算法快速稳定获取目标相对模型粗配准参数，使得目标点云与CAD模型大致重合；进一步采用ICP精确配准，实现点云中重合区域同名点对的完全匹配。

3.3标定Tj时刻目标相对位姿基准

以Tj时刻目标所处状态作为位姿基准，根据第一步时间微分方法获取该时刻目标瞬时运动特性，还原Tj时刻目标可测部位真实点云形貌，为该时刻目标相对位姿测量提供基础。Tj时刻目标相对位姿真值的获取通过上一步与三维重建获取的CAD模型配准值获取，该时刻相对位姿不仅作为将来时刻目标相对位姿增量叠加的基准，同时也作为自标定问题标准值的输出。

4 同向差分扫描方法可行性的地面验证试验

为了证明1.1差分扫描点云畸变规律不变性，进而验证本文提出的同向差分扫描方法在非合作目标相对位姿测量中的可行性，分别应用MATLAB 2014a以及VS2013和PCL(Point cloud library)，对上述思想逐一进行仿真实验与验证。

4.1获取目标卫星三维点云模型

已知尼康激光扫描仪获取的卫星模型三维点云，扫描点云密度为5 mm×5 mm，整体尺寸1.88 m×0.65 m×0.60 m，点云可视化后及相应逆向重建效果如图8所示：

4.2模拟雷达噪声

激光雷达信号在真空传播过程中，由于散斑效应、目标场景反射特性、背景噪声和接收机噪声等因素的影响，回波信号的功率可能出现较大幅度的起伏，所成距离像中的某些像素严重偏离真实的距离值，本文针对影响激光雷达成像质量中的散斑效应和接收机噪声分别给出噪声等效功率模型，并根据此模型对目标点云添加等效噪声，噪声等效功率模型为

(9)

式中：Pr,speck为散斑效应的回波功率；Et为接收机噪声功率；并且满足

(10)

(11)

式中：Ss为散斑噪声的强度，与散斑个数M、随机变量均值S、光学系统孔径和散斑大小等相关[17]，见式(12)；Pr为理想状态下的回波功率。

(12)

式(11)中：k为玻尔兹曼常数；T为绝对温度；B为接收机带宽；N为噪声因子；RL为负载电阻；ψi为探测器电流响应度。噪声效果见图9。

4.3获取雷达畸变点云

一般情况下失稳卫星自旋角速率约为15°/s,这里自定义旋转轴过模型质心，方向为(0, 0, 1)，且目标短时间内做匀速位移，假设三个方向速率分别为：vx=10 m/s,vy=6 m/s,vz=2 m/s。

线阵雷达单次扫描周期，即0.5 s，目标旋转7.5°，经过统计可测部位扫描线数，可以推算每一条扫描线绕自旋轴畸变角度。为了更好地展示畸变效果，图10为自旋角速率60°/s的模型(目标竖直方向总体畸变30°)。

第一次扫描结束后，雷达开始同向差分扫描，模拟扫描畸变点云数据如图11所示。目标相比上一次扫描开始时刻自旋30°，竖直方向总体畸变30°。

4.4点云配准与目标运动参数的获取

具体配准效果为：所处理的单组点云数量最大值为24981个点；配准算法基于PCL点云库，并在此基础上添加正态分布算法作为精配准粗值以降低配准迭代周期，提高算法鲁棒性；数据更新率为5 Hz。(当前地面试验搭载的计算机配置为：Core i5 2.50 GHz处理器、4G内存)，见图12。

根据式(3)，通过配准将同时获取相邻扫描时间内目标的位移增量X、Y、Z和自旋增量θ，将其代入式(5)即获取目标在该时间段内的运动参数，部分目标位姿增量情况见表1。

表1 位姿增量Table 1 Pose increment

4.5畸变恢复与三维重建

将上一步获取的目标运动参数代入式(6)，实现目标可测部位点云的畸变恢复如图13所示。

以雷达单周期扫描时间内目标运动7.5°为例，重建目标完整形貌至少需要雷达扫描48次。在模拟重建工作的试验中依次完成了以下工作内容：1)任意水平视角方向，360° 均匀获取目标模型48次；2)以上一步畸变恢复模型为依据，对48组畸变数据同步恢复；3)以第一组数据为基准坐标系，将48组数据按照对应的旋转平移矩阵转换到第一个点云的统一坐标系中；4)借助ICP算法，抽样配准数据，验证上述重建精度。重建效果见图14。

4.6增量累计误差自标定与目标相对位姿获取

1)误差来源分析

①激光雷达测量精度误差，基于ToF测距原理获取的点云三维坐标信息在计算机运算时存在光速常量、圆周率等舍入误差及设备自身测量延迟误差；②截断误差：计算目标瞬时位姿增量时所采用的的配准方式是一种优化迭代算法无法得到理想的精确解，而优化近似解与真实增量值存在一定截断误差。伴随每次组内迭代配准获取位姿增量的过程中都会不可避免的出现误差情况，由此一定时间后的位姿增量叠加必然出现误差累计的情况。

2)累计误差自标定

已知目标相对位姿增量真值：X=5 m，Y=3 m，Z=2 m,φ=0°,φ=0°，θ=7.5°。通过图15的相对位姿增量测量值与真值的对比观察，发现误差趋势在一定范围内随机波动而并无明显规律可寻，由此有必要对相对位姿增量的累计误差进行自标定。

由表1与图15的统计结果发现，位移增量误差绝对值小于0.01 m，角度误差绝对值小于0.25°，根据项目指标要求精度(相对位移测量精度≤0.10+(ρ-15)×0.0014 m，相对姿态测量精度≤1°)，可以计算最大位姿增量累计次数阈值为4。

3) 获取目标相对位姿

首先将解算的组内目标运动参数代入式(6)，获取既定时刻可测部位点云的真实坐标位置与整体形貌；其次以最大位姿增量累计次数阈值判定位姿基准；最后将既定时刻目标真实点云与基准三维模型配准，输出值即为目标在该时刻的相对位姿。

5 结 论

本研究以解决高轨道失稳非合作目标实时相对位姿测量为目的，针对线阵扫描型激光雷达测量动态目标发生畸变、影响配准精度以及算法延时无法满足实时性测量问题，根据畸变目标点云瞬时拓扑结构不变性，采用同向差分扫描方式，配准获取相邻扫描间隔时间内畸变点云位姿增量。该方案的优势在于仅使用单一载荷(线扫描激光雷达)且不依赖尺度因子来实现对动态非合作目标的三维重建、位姿增量累计误差自标定，为解决高轨失稳目标实时相对位姿测量难题提供一种新的研究思路。

[1] 闫海江, 范庆玲, 肖余之. DARPA地球静止轨道机器人项目综述[J]. 机器人, 2016, 38(5):632-640. [Yan Hai-jiang, Fan Qing-ling, Xiao Yu-zhi. Review of DARPA’s geostationary earth orbit robotic programs [J]. ROBOT, 2016, 38(5): 632-640.]

[2] The UCS Satellite Database. Union of concerned scencetists(UCS),Cambridge,Massachusetts,US[EB/OL].2016[2016-6-30].http://www.ucsusa.org/satellite_database.

[3] 梁斌, 徐文福, 李成. 地球静止轨道在轨服务技术研究现状与发展趋势[J]. 宇航学报, 2010, 31(1):1-13. [Liang Bin, Xu Wen-fu, Li Cheng. Research status and development trend of on orbit servicing technology in geostationary orbit [J]. Journal of Astronautics, 2010, 31(1): 1-13.]

[4] 梁斌, 杜晓龙, 李成. 空间机器人非合作航天器在轨服务研究进展[J]. 机器人, 2012, 34(2): 243-256. [Liang Bin, Du Xiao-long, Li Cheng. Advances in space robot on orbit servicing for non-cooperative spacecraft [J]. Robot, 2012, 34(2): 243-256.]

[5] Sharma S, Amico S. Comparative assessment of techniques for initial pose estimation using monocular vision [J]. Acta Astronautica, 2016, 123(1): 435-445.

[6] Li R H, Zhou Y, Chen F. Parallel vision-based pose estimation for non-cooperative spacecraft [J]. Advances in Mechanical Engineering, 2015, 7(7): 118,124.

[7] 蔡晗, 张景瑞, 翟光. GEO非合作目标超近距相对位姿视觉测量[J]. 宇航学报, 2015, 36(6):715-722. [Cai Han, Zhang Jing-rui, Zhai Guang. Relative pose determination for GEO non-cooperative spacecraft under the ultra-close distance [J]. Journal of Astornautics, 2015, 36(6): 715-722.]

[8] 梁斌, 何英, 邹瑜. ToF相机在空间非合作目标近距离测量中的应用[J]. 宇航学报, 2016, 37(9):1080-1088. [Liang Bin, He Ying, Zou Yu. Application of ToF camera for relative measurement of non-cooperative target in close range [J]. Journal of Astornautics, 2016, 37(9): 1080-1088.]

[9] 刘玉, 陈凤, 王盈. 基于激光雷达的航天器相对位姿测量技术[J]. 红外与激光工程, 2016, 45(8): 189-194. [Liu Yu, Chen Feng, Wang Ying. Measurement of relative position and pose between two spacecrafts based on laser lidar [J]. Infrared and Laser Engineering, 2016, 45(8): 189-194.]

[10] 冯春, 吴洪涛, 陈柏. 基于多传感器融合的航天器间位姿参数估计[J]. 红外与激光工程, 2015, 44(5):1616-1622. [Feng Chun, Wu Hong-tao, Chen Bai. Method for relative pose parameters between spacecrafts based on mixing of multi-sensor [J]. Infrared and Laser Engineering, 2015, 44(5): 1616-1622.]

[11] Qin X, Mao J. Noise reduction for lidar returns using self-adaptive wavelet neural network [J]. Optical Review, 2017(1): 1-12.

[12] Miller L K, Masciarelli J, Rohrschneider R. Critical advancement in telerobotic servicing vision technology [C]. AIAA SPACE Conference & Exposition, California, USA, Aug 30-Sept 2, 2010.

[13] Christian J A, Hinkel H, Dsouza C. The sensor test for orion relnav risk mitigation development test objective [R]. Houston: America Institute of Aeronautics, June 2010.

[14] 杜小平, 赵诗玥, 宋一铄. 国外空间目标操控相对位姿测量技术比较研究[J]. 装备学院学报, 2013(5):58-62. [Du Xiao-ping, Zhao Shi-yue, Song Yi-shuo. Comparative studies on relative-pose measurements in foreign space operations for targets [J]. Journal of Academy of Equipment, 2013(5): 58-62.]

[15] Ruel S, Luu T, Berube A. Space shuttle testing of the TriDAR 3D rendezvous and docking sensor [J]. Journal of Field Robotics, 2012, 22(4): 535-553.

[16] Russell S P, Rock S M. Particle filtering range data for pose estimation under torque-free motion[C]. The 14th IASTED International Conference on Robotics and Applications, California, USA, Jan 1-4, 2009.

[17] 王盈, 黄建明, 刘玉. 空间目标激光雷达成像仿真技术[J]. 红外与激光工程, 2016, 45(9):102-107. [Wang Ying, Huang Jian-ming, Liu Yu. Simulation of lidar imaging for space target [J]. Infrared and Laser Engineering, 2016, 45(9): 102-107.]

AMethodofRelativePoseMeasurementbySingleLoadforGEOInstabilityTarget

LI Rong-hua1,2, LI Jin-ming1, Chen Feng2, Xiao Yu-zhi2

(1. School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116028, China; 2. Shanghai Institute of Aerospace Systems, Shanghai 201109, China)

Considering the distortion of point cloud data during the detection of high orbit instability target by linear array scanning Lidar, a method for co-rotating differential scanning is described in this paper. The method is not to rely on multiple sensors to recover the distorted point cloud information, and finally to measure the relative position and orientation of a target. It bases on the topological instantaneous invariance of the distorted point cloud information of a moving target. Firstly, in this method, the motion increment and instantaneous motion parameters of the target are obtained by registration of the distorted point cloud in the adjacent scanning time. Secondly, restore the real geometric position of the distorted scanning line point cloud so as to complete the three-dimensional reconstruction of the target. Then take the target 3D model as the initial pose datum, which is updated continuously by setting the increment frequency threshold. Finally, the relative pose of the target is obtained through superimposing the motion increment. Under the condition of missing the prior information of the non-cooperative target, this method, by only using a single load, not only realizes the reconstruction of the target 3D point cloud model, but also measures the relative pose of the spatial non cooperative target accurately and efficiently.

Co-rotating differential scanning; Distortion recovery; Self calibration; Pose increment

V448.2

A

1000-1328(2017)10- 1105- 09

10.3873/j.issn.1000-1328.2017.10.011

2017- 06- 12;

2017- 08- 21

国家自然科学基金(51505059)；辽宁省自然科学基金(201602121)；上海航天科技创新基金(SAST2016016)

李荣华(1983-)，男，副教授，主要从事空间非合作目标三维位姿测量技术研究。

通信地址：辽宁省大连市沙河口区黄河路794号大连交通大学S-616(116028)

电话：15840612150

E-mail: lironghua705@163.com