两种着陆模式下的着陆器缓冲机构构型优化
吴宏宇,王春洁,2,丁宗茂,丁建中,刘学翱
(1. 北京航空航天大学机械工程及自动化学院,北京 100083;2. 北京航空航天大学虚拟现实技术与系统国家重点实验室,北京 100083)
两种着陆模式下的着陆器缓冲机构构型优化
吴宏宇1,王春洁1,2,丁宗茂1,丁建中1,刘学翱1
(1. 北京航空航天大学机械工程及自动化学院,北京 100083;2. 北京航空航天大学虚拟现实技术与系统国家重点实验室,北京 100083)
分别建立了着陆器在非0高度关机着陆模式下、触地关机着陆模式下的动力学仿真模型。基于仿真模型,应用全因子实验设计方法分析了着陆器在两种着陆模式下的软着陆性能,得到了软着陆极恶劣工况。为了获得软着陆性能最佳的着陆器设计方案,研究了着陆缓冲机构构型参数对软着陆性能的影响。结合仿真模型与实验设计方法获取样本点,构造了极恶劣工况下描述软着陆性能指标值、着陆缓冲机构构型参数之间映射关系的响应面模型。之后利用响应面模型与第二代非劣排序遗传算法(NSGA-II)实现了着陆缓冲机构构型参数的优化。将优化后的参数代入仿真模型验证,着陆器在两种着陆模式下的抗翻倒能力、底面抗损坏能力均得到提升。
腿式着陆器;着陆模式;动力学分析;响应面模型;优化设计
0 引 言
腿式着陆器现已被广泛应用到世界各国的深空探测任务中[1],例如美国的阿波罗号载人登月舱、美国的海盗号火星探测器、我国的嫦娥三号月球探测器等。我国最新公布的火星探测计划也将使用腿式着陆器完成深空探测任务。作为常用的深空探测设备,腿式着陆器的研究工作需要持续进行。考虑着陆器物理样机的制造及实验成本较高,有必要利用动力学仿真方法验证着陆器的软着陆性能。另外,在研制阶段对着陆器进行优化设计,有助于设计出软着陆综合性能最佳的着陆器。
国内外学者对于腿式着陆器的性能分析与优化设计已经进行了大量的研究工作。文献[2]通过理论分析,提出了腿式着陆器用缓冲器缓冲性能的评价方法;文献[3-8]使用数值仿真方法分析了着陆器的软着陆过程,确定了影响着陆器软着陆性能的主要因素;文献[9-10]考虑着陆工况的不确定性,基于蒙特卡罗法分析了着陆器的软着陆稳定性;文献[11-13]针对着陆器的抗翻倒能力和缓冲装置的吸能能力,考虑不同的着陆工况参数,绘制了着陆器安全着陆的稳定性边界;文献[14]基于响应面模型,针对单一着陆工况,对着陆器的着陆缓冲机构进行了优化设计;文献[15]针对多组极恶劣工况,优化了着陆器的着陆缓冲机构。以上文献均针对非0高度关机着陆模式开展研究,而文献[16-17]则针对触地关机着陆模式,应用ADAMS软件分析了该着陆模式下的着陆器软着陆性能,并给出了提升软着陆性能的方法。
上述文献研究了腿式着陆器的性能分析方法与单一着陆模式下的着陆缓冲机构优化方法,但同时考虑多种着陆模式对着陆器进行优化设计的研究较少。由于着陆器实际应对的空间环境复杂多变,为保证其可靠软着陆,需为其设计多种软着陆模式,即当首选着陆模式失效时,备选着陆模式依旧可以保证着陆器安全软着陆。因此,同时考虑多种着陆模式,对着陆器进行优化设计具有重要意义。本文基于响应面模型与多目标优化方法,考虑某型着陆器的两种着陆模式,对其缓冲机构进行了优化。优化后的缓冲机构使着陆器在两种着陆模式下的软着陆性能均得到提升。
1 着陆器动力学建模
1.1机械系统动力学建模
本文所研究的着陆器由主体及四套对称分布于主体周围的着陆缓冲机构组成。四套缓冲机构的构型与尺寸完全相同,均由主支柱、辅助支柱、足垫和缓冲杆组成,如图1所示。主支柱的上端与缓冲杆使用万向节连接、下端与足垫固连,主要起支承作用。辅助支柱与主体使用万向节连接,与主支柱使用球铰连接,其内外筒之间装有缓冲元件以吸收冲击载荷。缓冲杆的上端与主体固联,主要通过弯曲变形的方式吸收冲击载荷。
本文应用ADAMS软件实现着陆器动力学仿真模型的建立。为了提高仿真效率,模型中的小变形构件均简化为刚体,大变形构件则通过等效方法模拟其作用效果[18]。
辅助支柱内部缓冲元件的作用效果通过添加与辅助支柱内外筒相对位移(D)相关的力(FD)来模拟。FD与D的关系曲线利用有限元软件求得,如图2所示。
缓冲杆通过弯曲变形的方式缓冲主支柱传递来的冲击力,其动力学分析模型采用文献[18]提出的刚体等效方法建立,如图3所示。图中,αb表示缓冲杆受弯时的等效转角,M表示缓冲杆受弯时的等效转矩,S表示缓冲杆受弯时的等效轴向位移。αb与M,αb与S的关系曲线利用有限元软件求得,如图4所示。
本文将足垫与着陆面之间的相互作用力分解为法向冲击力与切向摩擦力,法向冲击力与切向摩擦力分别采用非线性阻尼弹簧模型与库伦摩擦模型模拟[4,15-18]。
1.2主发动机及姿控推进器推力等效模型
为了实现着陆过程的制动与调姿,着陆器装有一个用于制动的主发动机与若干用于调姿的姿控推进器[19-20]。在后文的研究中,将考虑主发动机与姿控推进器的作用效果,因此需建立模拟主发动机与姿控推进器推力作用效果的等效模型。
本文考虑的姿控推进器共有10台,其中2台位于主体上方,喷口方向平行于主体上表面、垂直于探测车驶离方向,编号为A1、A2。另外8台位于主体下方,喷口方向垂直于主体下表面,编号为B1~B8。10台推进器的位置如图5所示。
为了实现10台姿控推进器的控制,定义着陆器的控制坐标系如下:
XC轴:通过主体的几何中心,垂直于主体上表面,指向天空方向为正;
YC轴:位于主体上表面内,与XC、ZC方向构成右手系;
ZC轴:位于主体上表面内,与探测车驶离方向成45°夹角。
当处于1-2-1着陆工况时,控制坐标系示意图如图6所示。
在着陆器着陆过程中,测得着陆位置东(Y)-北(Z)-天(X)坐标系按照Z-X-Y的转序转到与控制坐标系平行位置时绕自身X、Y、Z轴转过的角度θX、θY、θZ,再测得控制坐标系相对于东-北-天坐标系的角速度在控制坐标系XC、YC、ZC轴的投影值ωX、ωY、ωZ。根据推进器控制策略可得各姿控推进器起作用时的推力函数如式(1)~(10)所示[16,20]。
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
其中,FA1、FA2表示A1、A2推进器的推力值,FB1~FB8表示B1~B8推进器的推力值。FM1与FM2分别表示A与B系列推进器可提供的最大推力值,ai、bi、ci均为与推进器控制策略相关的常数,上述参数取值根据文献[16]确定。
主发动机位于主体下方中心位置,喷口方向垂直于主体下表面。在关机指令发出前,主发动机推力方程如式(11)所示[16]。
(11)
其中,F表示主发动机推力值,ML表示着陆器整机质量,vx表示着陆器竖直速度。
在仿真模型主体上,对应主发动机、姿控推进器的位置处施加与主发动机、姿控推进器喷口方向相反的力,分别用来模拟主发动机与姿控推进器的作用效果。在仿真模型中建立实时测量,测得θX、θY、θZ、ωX、ωY、ωZ与vx的值,并根据式(1)~(11)更新各推力的取值,最终建立了主发动机及姿控推进器的推力等效模型。
2 着陆器的软着陆模式
本文研究的着陆器在正常工作状态下将采用非0高度关机模式(mode1)实现软着陆。该着陆模式下,着陆器通过高度传感器感知当前位置与星球表面之间的距离,在上述距离满足预定值时,着陆器关闭所有发动机,之后作自由落体运动直至足垫与着陆面接触后由缓冲机构吸收剩余冲击能量,实现稳定软着陆。
若非0高度关机模式出现故障导致主发动机无法及时关闭,则着陆器在下降过程中将受到主发动机产生的持续“地面效应”,软着陆稳定性将严重下降[21-22]。为了可靠关闭主发动机,着陆器的足垫装有触地敏感器感知触地动作,当非0高度关机失败时,则由触地敏感器发出关机信号以关闭主发动机,保证稳定软着陆,将上述关机方式称为触地关机着陆模式(mode2)。鉴于文献[17]的结论,在触地关机模式下,开启姿控推进器进行实时姿态调整,有助于提高着陆器的软着陆稳定性。考虑触地敏感器的信号采集时间与主发动机关机后效,主发动机的推力变化过程如图7所示。此外,从关机指令发出到姿控推进器推力开始下降的时间间隔为0.4 s,此段时间内姿控推进器正常工作,其推力从开始下降到降为0 N的时间间隔可忽略不计。
利用第1节所述方法分别建立两套动力学仿真模型。其中一套不包含主发动机及姿控推进器的推力等效模型,另一套则包含上述等效模型,两套模型分别用于分析着陆器在非0高度关机着陆模式下与触地关机着陆模式下的软着陆性能。
3 软着陆性能分析及极恶劣工况的确定
3.1软着陆性能判据
本文的研究内容主要针对着陆器的着陆稳定性。根据探测任务要求,着陆器的主要软着陆性能判据如下:
1)着陆器在着陆过程中不发生翻倒。即着陆器质心距包含相邻两足垫中心点的竖直平面的最小距离(LD)在着陆过程始终大于0,否则认为着陆器翻倒。且LD越大,着陆器抗翻倒能力越强[23];
2)着陆器在着陆过程中应避免底面与星球表面相撞。即着陆器尾喷管的底面中心点与星球表面的最小距离(HM)在着陆过程始终大于许用值(350 mm)。且HM越大,着陆器底面越不易与星球表面相撞。
3.2着陆初始条件
为了提高仿真效率,动力学仿真模型从着陆器首个足垫触地的瞬间开始进行仿真计算。鉴于上文提到的两种着陆模式,不考虑着陆器未触地之前的主动控制误差,着陆器触地时水平速度、三轴角速度为0、主体质量约770Kg。考虑着陆器装有地貌识别系统,足垫落入凹坑或撞击石块的可能性极小。因此,将着陆初始条件简化为着陆面摩擦系数(μ)、着陆面坡度(α)、着陆偏航角(θp)和着陆器竖直速度(vx)如图8所示。
考虑着陆器的几何对称性,θp在0~45°之间取值即可覆盖评判软着陆性能所需的全部着陆工况。
因此,本文考虑着陆初始条件参数的取值如表1所示[9-10,17-18]。

表1 着陆初始条件参数取值Table 1 Range of parameters of initial landing conditions
3.3极恶劣工况的确定
基于两套动力学仿真模型,本文采用全因子实验设计方法分析着陆器在两种着陆模式下的软着陆性能。实验设计中设置α以2°为增量从0°增至12°,设置μ以0.1为增量从0.3增至0.5,设置θp以3°为增量从0°增至45°。根据全因子实验设计的原则,完成一种着陆模式下的软着陆性能分析共需要7×3×16=336次动力学仿真。通过仿真计算,得到两种着陆模式下LD与HM取得最小值的工况如表2~3所示,将表2~3所示的四组工况定义为极恶劣工况。

表2 非0高度关机着陆模式极恶劣工况Table 2 Worst landing conditions under shutdown at specified height landing mode

表3 触地关机着陆模式极恶劣工况Table 3 Worst landing conditions under shutdown at touchdown landing mode
仿真结果显示,着陆器采用非0高度关机着陆模式时,HM存在低于许用值的情况。为了提升着陆器在两种着陆模式下的软着陆性能,下文将基于4组极恶劣工况,对着陆器的缓冲机构进行优化设计。
4 缓冲机构构型优化
4.1优化设计变量的确定
为了使着陆器整体结构满足在运载火箭中的安装要求,无法调整辅助支柱与主体的连接点位置、辅助支柱与主支柱的连接点相对于足垫的位置、主支柱与缓冲杆的连接点位置与缓冲杆与主体的连接点位置。在满足上述要求的前提下,能够进行优化调整的构型参数有足垫中心至着陆器中心轴的水平距离(dz)、主缓冲支柱的长度(LM)及辅助支柱可提供的缓冲力大小。其中,dz与LM的几何含义如图9所示,辅助支柱提供的缓冲力大小以缓冲力缩放倍数(kz)描述。后文将分析可调的构型参数对着陆器软着陆性能的影响,以确定本文的优化设计变量。
本文通过控制变量的方式分析dz、LM和kz对着陆器软着陆性能的影响,分析结果如下:
1)保持dz和kz不变,LM的增大将使着陆器整机高度提升,虽能够降低HM超出许用范围的可能性,但由于质心的提高也将使着陆器的抗翻倒能力降低。反之,则将增大HM超出许用范围的可能性,增强着陆器抗翻倒能力。
2)保持dz和LM不变,kz的增大将使软着陆过程中辅助支柱的缓冲行程减小,从而降低HM超出许用范围的可能性,但kz的增大同样也使着陆器着陆过程中的质心下降量减小而降低了其抗翻倒能力。反之,则将增大HM超出许用范围的可能性,增强着陆器抗翻倒能力。
3)保持kz和LM不变,dz的增大将使足垫间距离增大并降低着陆器整机质心,此时着陆器不易发生翻倒,但由于整体结构的降低也增大了HM超出许用范围的可能性。反之,则将减小HM超出许用范围的可能性,降低着陆器的抗翻倒能力。
根据以上分析结果,三项构型参数对软着陆性能的影响较为复杂,难以做出初步筛选。因此,本文选取全部三项参数作为设计变量对缓冲机构构型进行优化。根据设计要求,dz、LM和kz的初值与取值范围如表4所示。

表4 设计变量范围及初值Table 4 Initial values and range of design variable
4.2响应面模型的建立
采用优化算法所需迭代次数较多,而动力学仿真模型计算时间成本较高,若仍利用仿真模型计算着陆器的软着陆性能指标值将影响优化效率。为此,本文采用式(12)所示的完全四阶多项式响应面模型建立LD、HM与dz、LM、kz的映射关系,利用响应面模型进行优化迭代计算将大幅度提高计算效率。
(12)
式中:x1、x2、x3分别表示三个输入变量,βi表示多项式的各项系数。利用实验设计获得输入变量样本点,将n个样本点代入仿真模型计算出对应的输出值,并将输入、输出数据代入式(12),得到向量表达形式的响应面计算模型如式(13)所示。
(13)

本文将表2、表3所示的4组极恶劣工况分别代入对应的两套仿真模型,得到四套着陆工况确定的仿真模型。针对上述四套仿真模型,采用优化拉丁超立方实验设计方法在设计变量取值范围内抽取40组输入变量样本点,代入仿真模型,对应计算出LD、HM。基于仿真结果,拟合出着陆器采用非0高度关机着陆模式在工况1下的LD近似表达式LD-mode1、着陆器采用非0高度关机着陆模式在工况2下的HM近似表达式HM-mode1、着陆器采用触地关机着陆模式在工况3下的LD近似表达式LD-mode2、着陆器采用触地关机着陆模式在工况4下的HM近似表达式HM-mode2。
本文利用均方根相对误差值(RMSE)和决定系数(R2)来检验响应面模型对样本数据的拟合精度,如式(14)、(15)所示。
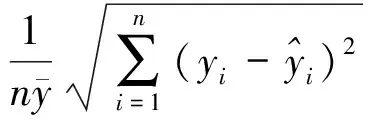
(14)

(15)
式中:n依旧表示输入变量样本点总数;yi表示仿真模型计算出的输入样本点对应的输出值;表示响应面模型估计值;表示yi的平均值。RMSE→0,R2→1说明响应面精度较高。表5为本文构建的响应面模型精度检验结果,其显示响应面模型可准确描述缓冲机构构型参数与软着陆性能指标值之间的映射关系。

表5 响应面模型精度分析Table 5 Accuracy analysis table of response surface models
4.3优化迭代计算及结果校验
上文的仿真结果显示,着陆器在两种模式下均不存在翻倒情况,但HM在非0高度关机模式下存在超出许用值的情况,因此本文的优化计算以最大化LD-mode1、HM-mode1、LD-mode2、HM-mode2为目标,以HM-mode1、HM-mode2不超过许用值为约束条件。为了防止优化后HM与许用边界重合,优化过程中将HM的许用值提
升为360mm。考虑触地关机模式为非0高度关机模式的备用方案,将LD-mode1与LD-mode2、HM-mode1与HM-mode2加权求和作为优化目标函数,构造优化数学模型如下。其中,加权系数可以根据不同的需求做出调整。
(16)
式中:x=(dz,LM,kz)T表示设计变量向量,x(L)与x(U)分别表示设计变量向量的下界与上界。
本文应用NSGA-II算法进行优化计算,算法参数配置如表6所示。

表6 优化参数设置Table 6 Value of optimal parameters
经过优化迭代计算,得到该优化问题的帕累托最优解集,根据帕累托最优解集,绘制帕累托前沿曲线如图10所示。
本文选取抗翻倒能力最强的缓冲机构构型作为最优构型,即最优解x*=(dz,LM,kz)T=(1411.736 mm,947.677 mm,1.107)T。将该组解代入仿真模型,并利用第3.3节方法获得新的极恶劣工况如表7~8所示。

表7 非0高度关机着陆模式极恶劣工况Table 7 Worst landing conditions under shutdown at touchdown landing mode

表8 触地关机着陆模式极恶劣工况Table 8 Worst landing conditions under shutdown at specified height landing mode
对比表2和表3可知,针对极恶劣工况,优化后的缓冲机构使着陆器采用非0高度关机着陆模式时的抗翻倒能力提升了4.77%、底面抗损坏能力提升了8.13%,使着陆器采用触地关机着陆模式时的抗翻倒能力提升了3.77%、底面抗损坏能力提升了5.87%。
5 结 论
本文应用ADAMS软件,分别建立了某型着陆器在非0高度关机着陆模式下、触地关机着陆模式下的动力学仿真模型,并结合仿真模型与全因子实验设计方法分析了着陆器在两种着陆模式下的软着陆性能,得到了软着陆极恶劣工况。根据仿真模型计算结果,建立了用于计算着陆器在极恶劣工况下软着陆性能指标值的完全四阶多项式响应面模型,并基于响应面模型与NSGA-II算法,实现了两种着陆模式下的着陆器缓冲机构构型优化计算。通过仿真模型验证,优化后的缓冲机构构型使着陆器在两种着陆模式下的软着陆性能均得到了提升。本文的优化设计结果对某型着陆器的设计具有指导意义,且本文的研究方法适用于其他型号着陆器的研制过程。
[1] 李萌. 腿式着陆缓冲装置吸能特性及软着陆过程动力学仿真研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. [Li Meng. Research on energy absorbers of legged-type lander and dynamic simulation on its soft landing process[D]. Harbin: Harbin Institute of Technology, 2013.]
[2] 刘荣强, 罗昌杰, 王闯, 等. 腿式着陆器用缓冲器缓冲性能及其评价方法研究[J]. 宇航学报, 2009, 30(3): 1180-1188. [Liu Rong-qiang, Luo Chang-jie, Wang Chuang, et al. Research on cushion properties and its evaluation methods of legged-type lander′s shock absorber[J]. Journal of Astronautics, 2009, 30(3): 1180-1188.]
[3] 王永滨, 蒋万松, 王磊, 等. 载人登月月面软着陆缓冲装置设计与分析[J]. 航天返回与遥感, 2015, 36(6): 22-28. [Wang Yong-bin, Jiang Wan-song, Wang Lei, et al. Research of landing gear technology of human lunar landing[J]. Spacecraft Recovery and Remote Sensing, 2015, 36(6): 22-28.]
[4] Nohmi M, Miyahara A. Modeling for lunar lander by mechanical dynamics software[C]. Modeling and Simulation Technologies Conference and Exhibit, San Francisco, USA, August 15-18, 2005.
[5] 蒋万松, 黄伟, 沈祖炜, 等. 月球探测器软着陆动力学仿真[J]. 宇航学报, 2011, 32(3): 462-469. [Jiang Wan-song, Huang Wei, Shen Zui-yi, et al. Soft landing dynamic simulation for lunar explorer[J]. Journal of Astronautics, 2011, 32(3): 462-469.]
[6] 丁建中, 王春洁, 王家俊, 等. 着陆工况对月球着陆器着陆缓冲性能影响分析[J]. 载人航天, 2016, 22(1): 132-137. [Ding Jian-zhong, Wang Chun-jie, Wang Jia-jun, et al. Effects of touchdown conditions on the buffering performance of the lunar lander[J]. Manned Spaceflight, 2016, 22(1): 132-137.]
[7] 岳帅, 聂宏, 张明, 等. 一种用于垂直降落重复使用运载器的缓冲器性能分析[J]. 宇航学报, 2016, 37(6): 646-656. [Yue Shuai, Nie Hong, Zhang Ming, et al. Analysis on performance of a damper used for vertical landing reusable launch vehicle[J]. Journal of Astronautics, 2016, 37(6): 646-656.]
[8] 陈金宝, 万峻麟, 李立春, 等. 月球探测器着陆性能若干影响因素分析[J]. 宇航学报, 2010, 31(3): 669-673. [Chen Jin-bao, Wan Jun-lin, Li Li-chun, et al. Analysis on the influencing factors of performance in lunar lander[J]. Journal of Astronautics, 2010, 31(3): 669-673.]
[9] Merchant D H, Sawdy D T. Monte Carlo dynamic analysis for lunar module landing loads[J]. Journal of Spacecraft and Rockets, 1971, 8(1): 48-55.
[10] Muraca R J, Campbell J W, King C A. A Monte Carlo analysis of the Viking lander dynamics at touchdown[R]. NASA-TN-D-7959, 1975.
[11] Maeda T, Otsuki M, Hashimoto T, et al. Attitude stabilization for lunar and planetary lander with variable damper[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(8): 1790-1804.
[12] Ponnusamy D, Maahs G. Development and testing of leg assemblies for robotic lunar lander[C]. The 14th European Space Mechanisms and tribology Symposium, Noordwijk, Holland, September 28-30, 2011.
[13] 朱汪, 杨建中. 月球着陆器软着陆机构着陆稳定性仿真分析[J]. 宇航学报, 2009, 30(5): 1792-1796. [Zhu Wang, Yang Jian-zhong. Touchdown stability simulation of landing gear system for lunar lander[J]. Journal of Astronautics, 2009, 30(5): 1792-1796.]
[14] 王家俊, 王春洁, 宋顺广. 基于响应面法的月球着陆器软着陆性能优化[J]. 北京航空航天大学学报, 2014, 40(5): 707-711. [Wang Jia-jun, Wang Chun-jie, Song Shun-guang. Performance optimization of lunar lander based on response surface methodology[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(5): 707-711.]
[15] 吴宏宇, 王春洁, 丁建中, 等. 基于多工况的新型着陆器软着陆性能优化[J]. 北京航空航天大学学报, 2017, 43(4): 776-781. [Wu Hong-yu, Wang Chun-jie, Ding Jian-zhong, et al. Soft landing performance optimization for novel lander based on multiple working conditions[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 776-781.]
[16] Wu H Y, Wang C J, Ding J Z, et al. Dynamics simulation analysis for novel lander based on two kinds of landing mode[C]. The 9th International Conference on Measuring Technology and Mechatronics Automation, Changsha, China: January 14-15, 2017.
[17] 丁宗茂, 王春洁, 吴宏宇, 等. 探测器触地关机软着陆稳定性分析[J/OL]. 2017[2017].http://kns.cnki.net/kcms/detail/11.2625.V.20170630.0901.003.html. [Ding Zong-mao, Wang Chun-jie, Wu Hong-yu, et al. Landing stability analysis of the explorer while using the footpad contact with surface as the signal for engine shutdown[J/OL]. 2017[2017].http://kns.cnki.net/kcms/detail/11.2625.V.20170630.0901.003.html.]
[18] 吴宏宇, 王春洁, 丁建中, 等. 不确定着陆环境下的着陆器缓冲机构优化设计[J/OL]. 2017[2017].http://www.cnki.net/kcms/detail/11.2625.V.20170324.1604.002.html. [Wu Hong-yu, Wang Chun-jie, Ding Jian-zhong, et al. Optimization design of landing gear under the uncertain landing environment[J/OL].2017[2017].http://www.cnki.net/kcms/detail/11.2625.V.20170324.1604.002.html.]
[19] 雷娟萍, 兰晓辉, 章荣军, 等. 嫦娥三号探测器7500N变推力发动机研制[J]. 中国科学:技术科学, 2014, 44(6): 569-575. [Lei Juan-ping, Lan Xiao-hui, Zhang Rong-jun, et al. The development of 7500N variable thrust engine for Chang’E-3[J]. Science China: Technology, 2014, 44(6): 569-575.]
[20] 张洪华, 关轶峰, 黄翔宇, 等. 嫦娥三号着陆器动力下降的制导导航与控制[J]. 中国科学:技术科学, 2014, 44(4): 377-384. [Zhang Hong-hua, Guan Yi-feng, Huang Xiang-yu,et al. Guidance navigation and control for Chang’E-3 powered descent[J]. Science China: Technology, 2014, 44(4): 377-384.]
[21] Doiron H H, Zupp G A. Apollo lunar module landing dynamics[C]. Structure Dynamics and Materials Conference and Exhibit, Atlanta, USA, April 3-6, 2000.
[22] 吴建云, 王春洁, 宋顺广. 月球探测器典型故障模式分析[J]. 宇航学报, 2014, 35(6): 633-638. [Wu Jian-yun, Wang Chun-jie, Song Shun-guang. Analysis of typical failure modes for lunar lander[J]. Journal of Astronautics, 2014, 35(6): 633-638.]
[23] Zupp G A, Doiron H H. A mathematical procedure for predicting the touchdown dynamics of a soft-landing vehicle[R]. NASA-TN-D-7045, 1971.
[24] Kurtaran H, Eskandarian A, Marzougui D. Crashworthiness design optimization using successive response surface approximations[J]. Computational Mechanics, 2002, 29(4-5): 409-421.
[25] Li M, Deng Z Q, Guo H W, et al. Optimizing crashworthiness design of square honeycomb structure[J]. Journal of Central South University of Technology. 2014, 21(3): 912-919.
ConfigurationOptimizationofLandingGearunderTwoKindsofLandingModes
WU Hong-yu1, WANG Chun-jie1,2, DING Zong-mao1, DING Jian-zhong1, LIU Xue-ao1
(1. School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100083, China;2. State Key Laboratory of Virtual Reality and Systems, Beijing University of Aeronautics and Astronautics, Beijing 100083, China)
The dynamic simulation models of a lander under two kinds of landing modes, namely, shutdown at the specified height landing mode and shutdown at the touchdown landing mode, are established. Based on the simulation models, the soft landing performance of the lander under two kinds of landing modes is analyzed by full factorial design, and the worst landing conditions are obtained. In order to get the optimal soft landing performance of the lander, the influence of the configuration parameters of the landing gear on the soft landing performance is studied. Aiming at worst landing conditions, the sampling points are obtained by using the simulation models and experiment design method, and the response surface models which reflects the mapping relationship between the configuration parameters of the landing gear and the values reflecting the soft landing performance are established. Then the configuration parameters of the landing gear are optimized based on the response surface models and the non-dominated sorting genetic algorithm II (NSGA-II). Finally, the simulation is carried out under two kinds of landing modes by using the optimized parameters. And it shows that both the ability of the lander to resist being overturned and the ability of the bottom of the lander to resist being damaged are enhanced.
Legged lander; Landing modes; Dynamics analysis; Response surface model; Optimization design
V423
A
1000-1328(2017)10- 1032- 09
10.3873/j.issn.1000-1328.2017.10.003
2017- 06- 19;
2017- 08- 14
国家自然科学基金重点项目(51635002)
吴宏宇(1993-),男,硕士生,主要从事航天机构的设计与动力学分析研究工作。
通信地址:北京航空航天大学新主楼B312(100083)
电话:(010)82316899
E-mail:hongyu@buaa.edu.cn
王春洁(1955-),女,博士,教授,主要从事数字化设计与仿真研究工作。本文通信作者。
通信地址:北京航空航天大学新主楼A802(100083)
电话:(010)82339818
E-mail:wangcj@buaa.edu.cn

