创新创业教育背景下高等数学教育模式的探讨
吕凤姣
(黄河科技学院 信息工程学院, 河南 郑州 450063)
创新创业教育背景下高等数学教育模式的探讨
吕凤姣
(黄河科技学院 信息工程学院, 河南 郑州 450063)
针对在创新创业教育背景下的高等数学教学方法所存在的问题进行探究,提出高等数学创新创业教育的新模式——问题牵引式教学法.以方向导数与梯度的概念为例,以问题牵引式教学思想为指导进行教学过程设计,更好地把高等数学的教学与实现优质人才培养目标统一起来.
创新创业教育; 高等数学; 问题牵引式教学法; 方向导数; 梯度
0 引言
随着中国经济和科学技术的飞速发展,数学的重要性也在其相互交会中日益凸显出来,创新教育对教育体系的调整至关重要,因此高等数学的教与学也倍感重要.当今倡导的基于创新创业教育而实行的高等数学教学,对于促进“学习型”人才培养模式向“应用型”人才培养模式的转变具有积极意义.高等数学作为理工科高校重要的专业基础课程,找到该课程与应用型高校人才培养相匹配的教学方法是十分重要的.笔者在认真分析创新创业教育特点的基础上,并结合我国自身教学实践和国际教学经验,提出了高等数学创新创业教育的新模式——问题牵引式教学法,希望能为高等数学教学方法提供新的参考.问题牵引式教学法是基于苏联教育家马赫穆托夫提出的“问题教学法”演变而来的.马赫穆托夫反对只注重知识传授的教学,要求引进科学实践的方式,把解决课题或问题作为教学的基本过程[1-3].
由于学习数学的最主要目的是应用,能够结合数学的思想方法,对实际问题给予恰当的解决.在高等数学教学中针对具体内容,适时实施问题牵引式教学,可以让学生更好地掌握数学知识,做到学以致用,从而激发他们学习数学的兴趣,提高他们的数学修养.问题牵引式教学法就是以“问题”牵引为主线组织教学,即以问题为中心,学生为主体,教师为主导,在教学中教师把教学内容设计成一系列问题,围绕知识点,层层设问,并指导和启发学生围绕“问题”积极思考,在一种问题氛围中促使学生掌握要点、难点、注意事项,从而达到学习知识和启迪思维的目的.本文以“方向导数与梯度”的概念为例,对教学的具体环节进行设计,以探讨高等数学教学中牵引式教学法的应用.
1 教学环节设计
1.1 陈述案例,提出问题,激发兴趣

图1 地形图Fig1 Topographic map
学生在学习高等数学的过程中,常常反映概念的引入、理论的建立过于抽象,感觉学习就是从概念到概念、由定理得到定理,与日常的生活实际联系不足,因此容易产生学习兴趣不浓的现象.为了避免这种情况,在方向导数与梯度的教学中,考虑创设合适的问题情境.实践证明,合适的问题情境能使学员的求知欲高涨,能充分调动学员的探索欲望和主观能动性.首先在PPT上播放一段山洪暴发的视频,当大家感受震撼画面的时候,老师提出问题.
案例南方某山区(地形图如图1)由于暴雨引发山洪,部分村舍被冲毁,地方政府决定择址重建安置受灾群众.通过相关部门勘测,现在地形图上标示了几个供选地点,请你从防洪的角度做出选择.
分析此案例取材于实际生活,具有很强的现实意义,从而使学生产生强烈的探索兴趣,为后续教、学创造了良好的情境.
1.2 分析案例,构建概念
案例的展示激发了学生的兴趣后,学生会进行激烈的讨论,但往往会缺失思考方向,讨论显得较为凌乱,这时就需要教师对学生的分析讨论进行引导,通过教学互动构建相关概念.
导语1新的选址应该避开可能形成的山洪线路,而“水往低处流”的经验告诉我们,真正应该关心的是水流下降最快的路径.由于山地表面可以视为一个二元函数的图像,因此我们需要从理论上讨论二元函数沿某一方向的变化率问题.
导语2这里提到了变化率,大家马上想到的是导数的概念,但是如何反映方向呢?对,利用向量的概念.由于问题只关心方向性,因此只采用单位向量即可.
导语3导数的本质是函数改变量与自变量改变量之比的极限.现在请大家模仿导数、偏导数的定义,讨论如何表述这种结合了方向的导数概念.
教学效果这样就引出了方向导数的概念,既避免了直接给出方向导数概念的抽象性,还为学员理解方向导数的实质、掌握方向导数的应用奠定了基础.
经过分析讨论后得出:

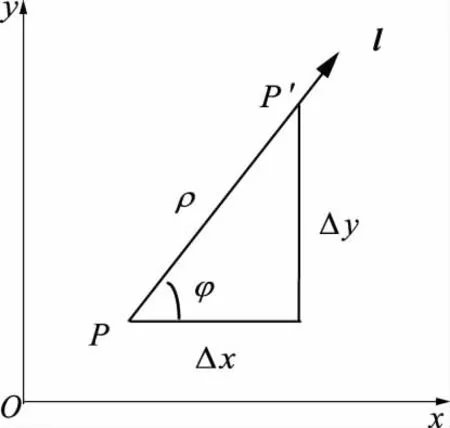
图2 方向导数的定义Fig2 The definition of directional derivative
定理1[4](方向导数的存在性)如果函数f(x,y)在点P(x,y)处是可微分的,那么函数在该点沿任意方向l的方向导数都存在,且有
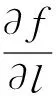
其中φ为x轴正向到方向l的转角.
教学效果通过引导学生对案例分析和对问题思考的逐步深入,构建出方向导数的概念,让学生体会和感受从实际问题中产生概念的思想过程.
1.3 深化问题,建立理论
在案例教学中,案例的作用不仅仅是作为引例激起学生的兴趣、引出概念,更应该在整个教学过程中紧紧围绕案例,通过引导学生对案例中提出的问题深入思考,以问题解决为指向,以已有知识为基础,经过创造性思维活动建立起相关的理论.
导语4前面经过大家的思考、讨论,类比导数的概念构建了方向导数的概念.请大家想想案例中的问题解决了吗?没有.因为我们要寻找山洪路线,也即是二元函数沿着什么方向的变化率最大?换个说法就是寻找使方向导数最大的方向.
导语5直接考察方向导数可能感觉无从入手,那么请大家注意在前面定义的l={cosα,sinα},然后尝试着对方向导数的表达式从向量运算的角度进行变形,可以得到什么结果呢?
导语6有同学将方向导数变形为向量的数量积形式,
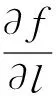
这种形式能帮助我们解决“方向导数最大”的问题吗?我们知道,当两向量同向时,数量积最大.那么除了l={cosα,sinα}外,另一向量叫什么,它有什么特点呢?
由此引入梯度的概念.
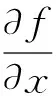
gradf(x,y)=f(x,y)=i+j,
进一步讨论可得梯度与方向导数的关系:
函数在一点的梯度是个向量,它的方向是函数在这点的方向导数取得最大值的方向,而它的模等于方向导数的最大值.
分析通过对问题的深入探讨,引导学生围绕“变化率最大的方向”这个问题,结合向量的运算性质,对方向导数的表达式进行形式转化,在问题解决的同时,自然地引入梯度的概念及其特点,使学生的理论思维得到训练.
1.4 解决问题,总结方法
利用通过案例分析、问题深化环节构建的概念和理论,对案例中的问题进行解决,是案例教学的关键环节,可以让学生体会到“实际—理论—实践”的过程.
导语7现在我们已经知道了梯度方向是方向导数取得最大的方向,也就是山洪的流向.那么如何在地形图上标示出山洪可能的路径呢?
导语8地形图上标示了山地的等高线,如果能找出梯度与等高线的位置关系,就可以以等高线为参照,绘出山洪流向.请大家分析讨论梯度向量与等高线之间的位置关系.
首先给出等高线的概念,并讨论得出梯度与等高线的关系:
函数在一点的梯度方向与等高线在这点的一个法线方向相同,且从数值较低的等高线指向数值较高的等高线(图3).
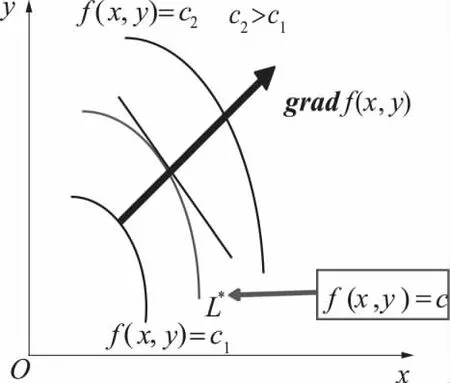
图3 等高线Fig3 Contour line
导语9大家讨论得到一点处的梯度向量垂直于过此点的等高线.现在就请大家在地形图上绘出山洪的形成和流经路线,从而对选址工作提供可靠的理论参考.为了使学生更直观地观察山洪流经路线,又借助Matlab数学软件画出了山洪流下路线.通过增加这一教学环节,使得数学教学变得更加生动有趣,还能培养学生几何直观能力及结合计算机解决问题的能力.
导语10希望大家通过本节课的学习,理解并体会方向导数和梯度的概念以及它们之间的联系,对于具体计算,是下节课要学习的内容.
分析通过回归案例,引导学生利用本堂课所建立的理论知识对问题进行解决,使学生真切地感受到知识从形成到应用的过程,同时使学生的认识得到升华.
2 结语
高等数学教学是高等教育的重要部分,在“大众创业,万众创新”的新时代口号下,更多地注重学生的实践能力变得越来越重要,要想将当今高等数学培养创新型人才的改革需要得到有效的使用,在传统的高等数学教学过程中,需要将学生的专业知识进行有效结合,有效利用问题牵引式教学法.与传统教学方法相比较占有一定的优势,是新时代教育下的一种素质教育,它既注重学生问题意识的培养,又注重学生数学知识运用能力的培养,它把开放式教学和探究式教学融于一体,对培养学生创新意识和创新能力,提高学生分析问题、解决问题能力及综合运用知识的能力具有重要作用,完全符合新形势下国家对人才培养的需要,是一种具有重要意义的教学方法[5].实践表明,利用问题牵引式教学法,可以将学生的学习兴趣进行有效的激发,让学生产生主动求知欲,将学生的思路进行有效的拓宽,还可以为专业知识的学习奠定坚实的基础,使数学课堂教学效果得到有效的提高,完成新型人才培养的目标.
[1] 黄刚.高等数学教学与应用型高校人才培养的对接[J]. 曲靖师范学院学报,2015,34(3):25-26.
[2] 田苗,白雪洁,李春兰.大学数学案例教学法的研究与实践[J].河北农业大学学报(农林教育版),2012,14(2):76-77.
[3] 杨雯靖.“高等数学”教学中数学思维与创新能力的培养[J].中国电力教育,2010,29(24):135-142.
[4] 同济大学应用数学系.高等数学[M].7版.北京:高等教育出版社,2014:103-111.
[5] 王慧敏.高等数学教学提高学生数学应用能力的策略[J].西部素质教育,2016,17(15):166-180.
DiscussiononHigherMathematicsEducationModeintheBackgroundofInnovationEducation
LV Fengjiao
(CollegeofInformationEngineering,HuangheScienceandTechnologyCollege,Zhengzhou450063,China)
Aiming at the problems existing in the teaching methods of higher mathematics in the background of innovation education, a new model of higher mathematics innovation education, problem based teaching method, is put forward. Taking the concept of directional derivative and gradient as an example, the teaching process under the guidance of problem based is designed. It is necessary to unify the teaching of higher mathematics with the goal of achieving high quality talents.
innovation education; higher mathematics; teaching method of problem based; directional derivative; gradient
2017-07-14
郑州市科技局基金项目(20141375)
吕凤姣(1983—),女,河南商丘人,黄河科技学院信息工程学院讲师.
10.3969/j.issn.1007-0834.2017.03.013
G642.0;O172.1
A
1007-0834(2017)03-0058-04

