小波包和GA-SVM在轴承故障诊断中的应用

， ，

(西南交通大学 机械工程院,成都 610031)

小波包和GA-SVM在轴承故障诊断中的应用

蒋恩超，傅攀，张思聪

(西南交通大学机械工程院,成都610031)

为了解决傅里叶变换难以兼顾信号在时域和频域中的全貌和局部化特征以及支持向量机惩罚参数c和核函数参数g选取的问题，提出了基于小波包和GA-SVM的轴承故障诊断方法;首先通过实验采集多种工况下故障轴承和正常轴承的振动信号，从振动信号中提取能够表征轴承运行状态的时频域特征以及基于小波包分析的特征向量来作为GA-SVM的输入，然后在SVM的基础上，针对SVM的惩罚参数和核函数参数在不同应用场景下的取值难以确定的特性，采用了遗传算法对支持向量机进行参数优化的GA-SVM算法进行模式识别;实验结果显示，基于小波包和GA-SVM的轴承故障诊断方法比SVM和BP都具有更高的识别精度。

滚动轴承；模式识别；GA-SVM；参数优化

0 引言

滚动轴承是各种机械设备中应用最广、最容易发生故障的机械部件之一。如果机械设备的滚动轴承发生故障往往会导致设备运行不平稳，产生异常的振动和噪声，如果不及时进行维护，则会对设备造成损坏，更有甚者，则会导致灾难性的事故[1]。因此，对滚动轴承进行故障诊断有着重大的意义。

由于滚动轴承故障会产生异常的振动和噪声，因此往往通过采集滚动轴承的振动信号来进行故障诊断的研究，其中主要分为振动信号处理，信号特征提取，轴承状态识别这3个部分[2]。

傅里叶变换是20世纪70年代发展出来的一种分析方法, 是用一系列三角波来表示信号方程的方法[3]。傅里叶变换只能分别给出信号在时域或频域的统计平均结果，无法兼顾信号在时域和频域中的全貌和局部化特征。小波通过对信号进行伸缩或者平移等数学手段，对信号进行了更加多尺度，细化的分析，解决了傅立叶变换不能解决的许多困难，能有效的从信号中提取信息[4]，因此近几年来小波分析在信号处理领域得到了广泛的应用[5-6]。

支持向量机(support vector Machine,SVM)是一种机器学习方法，在90年代中期基于统计学习理论得到了发展，在90年代后获得了大量的应用，同时也在实际的使用过程中获得了良好的分类效果，表现出了广阔的应用前景[7]。但是在支持向量机的使用过程中其也存在着不少的问题，其中最大的问题在于支持向量机的分类效果在很大程度上受制于核函数参数和惩罚因子的选取。传统的参数选择方法是根据使用者的经验设定支持向量机的参数，但是在实际使用过程中发现，小幅的参数变化往往都会导致分类结果产生巨大偏差[8-9]。因此很多学者致力于研究支持向量机参数选取的方法，目前往往通过在交叉验证(CV)思想下使用网格法来寻找支持向量机最优的惩罚参数和核函数参数，但是这种方法存在大范围搜索时搜索效率低下的问题[10-12]。

遗传算法(genetic algorithms,GA)是一种智能优化方法，该方法不仅适用性广，而且操作相对简单。该方法的基本思路是通过拟自然界基因的遗传和复制机制对优化目标进行随机搜索优化[13]。针对支持向量机参数选取的特征，将遗传算法和SVM结合在一起，提出了一种基于遗传算法的参数优化方法，这种方法能筛选出最佳的核函数参数和惩罚因子，从而确定支持向量机模型。然后利用小波分解提取出轴承振动信号的特征作为支持向量机的输入，同时使用遗传算法对支持向量机的参数进行优化，建立基于GA-SVM的故障识别模型，为轴承故障诊断提供了更高的精度，是一种行之有效的方法。

1 信号采集

由于滚动轴承故障会产生异常的振动，因此采用振动传感器采集轴承的振动信号，实验装置如图1所示。在基座架上安装电机、联轴器、轴承、轴承座、减速箱、磁粉制动器等设备。

轴承安装在轴承座内，难以直接对轴承进行监测。所以本实验利用磁铁将振动传感器安装在轴承座上。

图1 实验平台

本实验中，变频器分别在25 Hz、30 Hz两种工况下工作，且每种工况下，又有正常和故障两种状态。两种状态各10个样本，共40个样本。

从采集的样本数据可以看到样本数据有零点漂移的现象，因此要对采集的原始数据进行零均值化处理。由于随机干扰信号的频带较宽，有时高频成分所占的比例还很大，使得由采集到的离散数据绘成的振动曲线呈现出许多毛刺，很不光滑。为了削弱干扰信号的影响，提高振动曲线光滑度，因此对采样数据进行五点三次平滑处理。图2为数据平滑处理后的频域图，从频域图形上看，高频部分明显变少变小，而低频部分基本无变化。因为故障的频率主要集中在低中频部分，这样处理不仅对故障的分析无影响,而且去除了部分噪音，减少干扰。

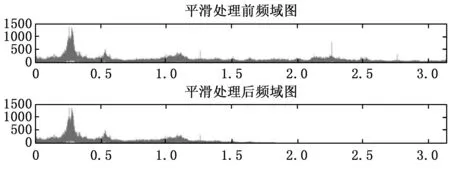
图2 平滑处理前后频域图

2 特征提取

2.1 时域特征计算

时域信号是振动信号的直观体现，在时域中往往也能提取出一些有用的特征。用xi来表示采集到的振动信号的时间序列(i=1,2,…,n)。常用的时域特征包括以下几种。

1)均方根值：

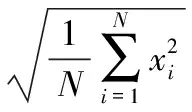
轴承的振动信号的均方根值往往和由轴承表面的不平顺而产生的无规则振动的波形有比较好的相关性。

2)峰值：

峰值由信号的一系列最大瞬时幅值取均值得到，他能够反映出信号的强弱，对表面点蚀等能够产生瞬时冲击的故障有比较好的适用性。

3)峰值因子：

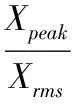
峰值因子是峰值除以均方根值。相比于峰值，峰值因子不会受到信号幅值大小的影响，因此对传感器的灵敏度的依赖性比较低，即使传感器的灵敏度产生变化，峰值因子也不会出现较大的变化。

4)脉冲因子：

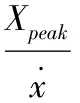
脉冲因子是峰值与绝对均值之比。和峰值一样，脉冲因子和故障产生的瞬时的冲击有较大的相关性。研究表明脉冲因子在故障前期会随着故障加剧而上升，当上升到一定程度后，反而会减弱。

5)波形因子：

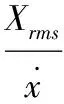
波形因子为均方根值与绝对均值之比。

6)峭度：

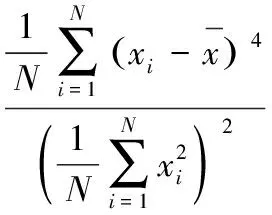
峭度系数取脉冲响应幅值的4次方为判断依据，拉大脉冲信号和背景噪声的差距以提高信噪比，用以表示大幅度脉冲信号出现的概率。其对轴承早期故障较敏感，是轴承故障简易诊断的重要依据。

7)裕度系数：

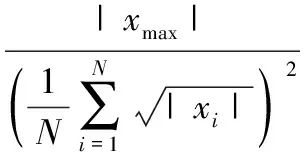
2.2 小波包理论和小波包特征计算

小波分解是把信号分解为许多基本小波的相加，这些基小波函数具有充分的光滑性且能在有限的区间内迅速衰减为零。

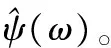
(1)

将母小波函数ψ(t)进行伸展或者压缩或者平移等操作便得到了一个小波基函数，对于一个确定的小波基函数，它对一维连续信号x(t)的连续小波变换为:

(2)

用u0(t)表示尺度函数，用u1(t)表示小波函数ψ(t)，hk(n)、gk(n)为共轭正交镜像滤波器组。则有：

(3)

定义：

(4)

则集合{un(t)}n∈Z为小波包。

使用小波方法提取信号的特征首先要对采样得到的振动信号进行小波包分解，然后计算各频带的能量。本文采用了db5作为小波基函数，对振动信号进行4层小波包分解后, 计算各个频带的能量。

抽取的特征要能够充分反映同类信号之间的相似性，又要充分表征不同状态信号间的差异性。本文参照特征计算结果，从信号的时域特征和小波包特征中共选取了11种满足条件的特征作为状态识别的输入。

3 GA-SVM故障诊断

3.1 遗传算法(GA)

遗传算法是一种适用性广，操作简单的智能优化算法，其主要思想是把问题的解编码为一个“染色体”群体，以挑选的适应度函数为准则，仿照自然界的淘汰机制对个体进行选择，交叉和变异等操作。最后得到满足条件的个体进行反编码得到最优解[11-13]。其主要算法流程如下：

Step1：对优化问题的解进行编码，确认种群的数量，产生种群的初始值。设置当前迭代代数为零。

Step2：根据优化目标确定合适的适应度函数，利用适应度函数计算个体的适应度，留下种群中适应度较好的个体。

Step3：采用轮盘选择算法对从当代群体中选择比较优良的个体进行选择操作，产生下一代群体。

Step4：从群体中按照一定比例任意选择染色体，两两进行随机的交叉操作，得到的新染色体和未进行交叉操作的染色体一起成为新的群体。

Step5：从群体中按照一定比例任意选择染色体进行变异操作，得到的新染色体和未进行变异操作的染色体一同成为新的群体。

Step6:重新计算新群中各个个体的适应度，如果群体中有个体的适应度大于当前最好适应度，则以该适应度取代当前最好的适应度。

Step7：当前迭代代数加1。如果当前迭代代数达到预置最大迭代代数或者最佳适应度个体达到要求则结束算法。否则重复Step3至Step6。

3.2 支持向量机(SVM)

支持向量机是一种分类方法，这种方法通过设计一个最大分类间隔器确定一个最佳分类平面来对样本进行分类。该最佳分类平面要能够获得最大稳定性和分类的确信度，从而拥有良好的推广能力[7-8]。

假设给定一个特征空间上的训练数据集

T={(x1,y1),(x2,y2),…,(xN,yN)}

(5)

其中x∈Rn,y∈{+1,-1},i=1,2,…,N,在特征平面中找到一个超平面w·x+b=0，使得其能对所有样本进行分类。定义几何间隔:

(6)

则构造最优超平面的问题可以转化为:

(7)

显然该问题是一个凸优化问题，有：

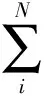
(8)

用d*来表示该问题的最优解，可以把问题转化为如公式(9)所示的对偶问题。

(9)

求解该问题先让L(w,b,ξ,a,r)关于w和b最小化，

即L(w,b,ξ,a,r) 关于w和b的偏导等于零，得到

(10)

则可求得:

(11)

因此有分类函数:

(12)

由于一般情况下的状态都是线性不可分的，对于出现线性不可分样本的情况，可以使用核函数方法，利用核函数建立一定的映射关系，将样本数据从二维空间映射到高维空间，在高维空间寻找一个能够对样本进行分类的超平面。设核函数的映射关系为K(xi,xj)，则分类函数的表达式为:

(12)

3.3 遗传算法改进支持向量机(GA-SVM)

在上一节关于SVM原理的叙述中我们可以发现传统的SVM在处理离散变量和引入核函数的环节中需要确认惩罚参数c和核函数参数g，两者的选择直接影响了支持向量机的分类精度和泛化能力。针对这种情况，目前往往通过在交叉验证(CV)思想下使用网格法寻找最优的惩罚参数c和核函数参数g。为了克服网格法在大范围内寻找最优参数的局限性。可以在传用交叉验证(CV)思想下采用遗传算法来搜索最优的参数。其流程如下所示。

Step1：采用二进制编码，对最佳惩罚参数c和核函数参数g进行编码。

Step2：确定适应度函数为CV意义下的准确率。

Step3：随机产生初始种群。设置当前迭代代数。

Step4：输入训练样本，计算种群个体的适应度，即CV意义下SVM的准确率。

Step5：判断个体适应度是否达到要求，如果达到要求，则对该个体进行解码。如果没达到要求，则对种群进行选择，交叉，变异操作，返回步骤4。

Step6：利用解码得到的最佳参数建立SVM模型。

Step7：利用该模型进行分类。

3.4 GA-SVM故障诊断实验

为了验证GA-SVM方法的有效性。通过实验对该方法进行验证。使用在第一节采集和处理后的40组实验数据作为本次实验的训练样本和测试样本。

基于3.3众多原理，利用matlab平台编程，建立GA-SVM模型。其中设置GA-SVM的种群数量为20，迭代代数为250，适应度函数为CV意义下的准确率。交叉率设为0.9，变异率设为0.2，取RBF核作为核函数，设置惩罚参数c的取值范围为[0,100]、设置核函数参数g的取值范围为[0,100]。

在2.2节中已经对第一节采集的40组实验数据进行了特征提取。得到了40组拥有11个特征的特征向量作为训练样本和测试样本，其中选取4种状态数据各4组共16组数据作为训练样本，其余24组作为测试样本。

使用16组数据通过遗传算法对支持向量机的参数进行寻优，最终得到的最佳惩罚参数为c=0.226、最佳核函数参数为g=0.537。

在编程过程中输入支持向量机的惩罚参数为c=0.226、核函数参数为g=0.537，建立支持向量机模型。利用该模型对剩余的24组数据进行分类。其测试结果如图3所示，其中1表示正常轴承，0表示故障轴承。从图3所示的结果可以看到GA-SVM识别的准确率达到了100%。说明GA-SVM本身具有很高的识别精度。

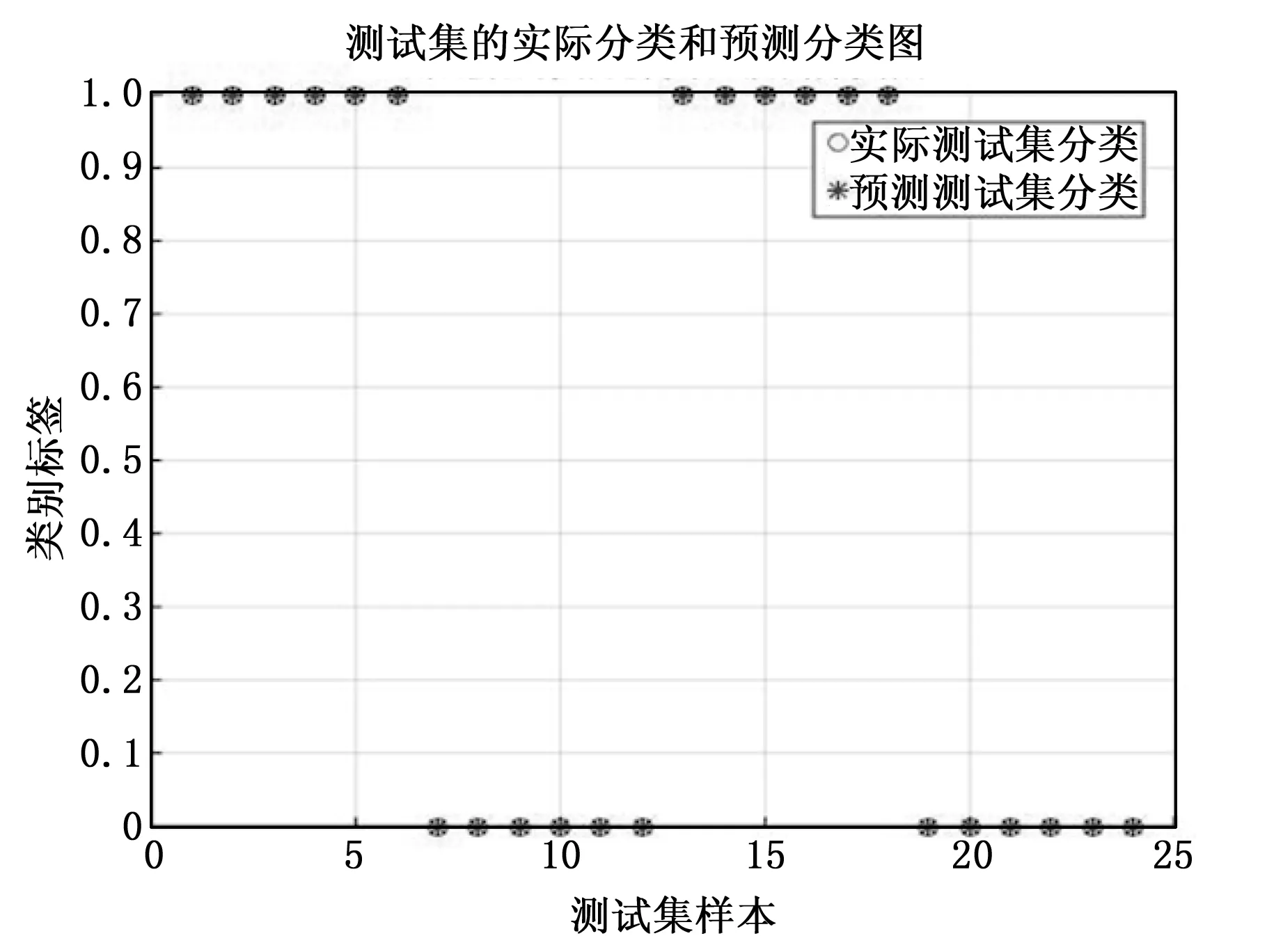
图3 GA-SVM分类结果

为了进一步检验GA-SVM在SVM参数寻优和状态识别上的效果，因此本实验设置了SVM模型和BP神经网络来识别轴承的状态。

其中由于在没有先验知识的情况下，SVM模型的惩罚参数c和核函数参数g需要人为根据经验进行设定，本实验选取惩罚参数为c=1，核函数参数为g=1.5。

BP网络是一种常用的神经网络，由于本文选取了11种特征参数作为特征向量，因此设置网络输入层个数为11层。根据最佳隐层单元数公式n2=2n1+1预计最佳隐层层数为23层，然后在23±3层范围内历遍隐层个数，根据误差最终确定隐层层数 25。输出层为两层，输出0,1分别表示故障轴承和正常轴承。同样选取4种状态数据各4组共16组数据作为训练样本，其余24组作为测试样本。

BP、SVM和GA-SVM模型的分类结果如表1所示。

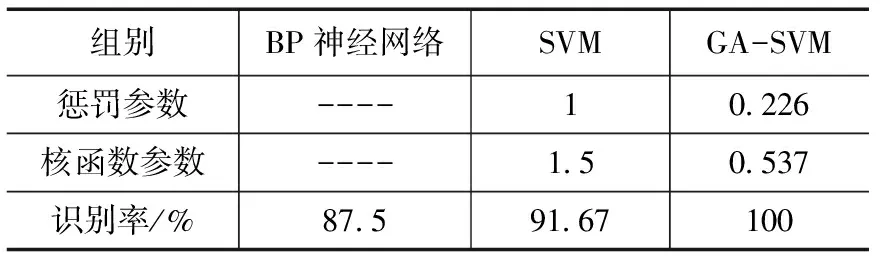
表1 BP、SVM、GA-SVM诊断结果

4 结论

对比SVM和GA-SVM，GA-SVM避免了惩罚参数c和核函数参数g选择的盲目性，寻找出一定范围内最佳的参数，有效的提高了支持向量机的识别精度。同时对比GA-SVM和BP神经网络的识别精度，GA-SVM在提高了支持向量机的识别精度的同时，其本身的模式识别效果也优于传统的识别方法。因此实验结果很好的体现了GA-SVM模式识别中的优越性，有效地提高了滚动轴承状态识别的精度。

[1]盛国裕．滚动轴承质量检验[S]．北京: 中国计量出版社，2005．

[2]Wu S D，Wu P H，Wu C W．et al.Bearing fault diagnosis based on multiscale permutation entropy and support vector machine [J]． Entropy，2012，14( 8) : 1343 - 1356．

[3]张贤达．现代信号处理[M]．北京:清华大学出版社， 2002．

[4]李 敏，傅 攀．EMD 和 Elman 神经网络在滚动轴承故障诊断中的应用[J]．四川兵工学报，2011(8):59-63．

[5]杨秀芳，张 伟，杨宇祥．基于提升小波变换的雷达生命信号去噪技术[J]．光学学报，2014,34(3):1-6．

[6]紫 阳，何正嘉，张周锁．小波分析技术及其在机械设备非平稳故障诊断中的应用[J]．西交通大学报．2004(9):82-87．

[7]克里斯特安尼，李国正．支持向量机导论[M]．北京：电子工业出版社，2004-1．

[8]张小燕，张 强．基于SVM的分类方法综述[J]．科技信息，2008(28)．

[9]Zhang X Y，Liang Y T，Zhong J，et al．A novel bearing fault diagnosis model integrated permutation entropy，ensemble empirical mode decomposition and optimized SVM[J]．Measurement，2015，69: 164-179．

[10]张小龙，张 氢，秦仙蓉,等．基于 ITD 复杂度和 PSO- SVM 的滚动轴承故障诊断[J]．振动与冲击，2016,24(35):102-107．

[11]杨 杰，郑 宇，刘 董,等．基于遗传算法的SVM带权特征和模型参数优化[J].计算机仿真，2008,25(9):113-118.

[12]张 庆，刘丙杰．基于PSO和分组训练的SVM参数快速优化方法[J]．科学技术与工程，2008,8(16)：4613-4616．

[13]常洪江．遗传算法综述[J]．电脑学，2010(3):115-116．

[14]窦丹丹，姜洪开，何毅娜．基于信息熵和 SVM 多分类的飞机液压系统故障诊断[J]．西北工业大学学报，2012，30(4): 529.

ApplicationofWaveletPacketandGA-SVMinBearingFaultDiagnosis

Jiang Enchao1，Fu Pan2，Zhang Sicong

(School of Mechanical Engineering，Southwest Jiaotong University，Chengdu 610031，China)

In order to solve the problem that Fourier transform cannot detect both full view and local feature in time domain and the problem of the action of penalty parameter and kernel function parameter of support vector machine selection．put forward a method of fault diagnosis of bearing based on wavelet packet and GA-SVM．First，Collect vibration signal of fault bearing and normal under various conditions and extract the characteristics which are typical in time domain and wavelet packet domain as the input of GA-SVM input．Then，on the basis of SVM，using the genetic algorithm to optimize the parameter of GA-SVM as the parameters of SVM are hard to put forward.．The experimental results show that the fault diagnosis method based on wavelet packet and GA-SVM has higher recognition accuracy than SVM and BP．

bearing；pattern recognition；GA-SVM；parameter optimization

2017-03-03；

2017-04-24。

蒋恩超(1993-)，男，浙江台州人，硕士研究生，主要从事智能化状态监测和故障诊断方向的研究。

傅 攀(1961-)，男，河南人，教授，主要从事先进测控技术与系统方向的研究。

1671-4598(2017)10-0007-04

10.16526/j.cnki.11-4762/tp.2017.10.003

TH133.33：TH16+.3

A