基于用户预约数据的公共自行车高峰期调度研究
靳文舟,叶钦海,郝小妮
(华南理工大学 土木与交通学院,广东 广州 510640)
基于用户预约数据的公共自行车高峰期调度研究
靳文舟,叶钦海,郝小妮
(华南理工大学 土木与交通学院,广东 广州 510640)
围绕公共自行车系统缺乏高峰期需求预测以及系统调度理念,引起调度滞后、用户满意度低等问题展开分析,探讨公共自行车高峰期调度需求预测和系统平均满意度量化的方法,研究公共自行车调度最优化路径问题。在基于用户预约数据的高峰期调度需求预测模型研究基础上,考虑用户满意度,建立最小化调度综合成本的优化调度模型,并采用改进的遗传算法对模型进行求解。以广州市某区域的公共自行车系统为研究对象,对模型进行实例验证。研究结果表明:与常规调度方案相比,综合成本降低了16.6%,系统平均用户满意度提升了28.7%。
交通运输工程;公共自行车;需求预测;系统平均满意度;优化调度;遗传算法
0引言
交通领域中,自行车交通因其独有的环保性以及便捷性,被认为是改善未来城市交通结构与缓解城市交通问题的良方。公共自行车作为公共交通的延伸,在国家明确提出“切实转变过度依赖小汽车出行的交通发展模式”的大背景下,得到各大城市的青睐,但与此同时,运营中的调度问题也日渐突出。资料显示,现状运营方一般采用人工巡查或实时监控的方式对各服务点进行监测,当服务点的车桩比例临近阈值时(小于0.2或大于0.8),发出调度预警信息,提示管理员安排调度。整个过程各环节随机性大,对用户真实需求缺乏准确预判;调度多针对单个服务点,缺乏系统整体调度;调度路径靠司机经验临时确定,无优化过程。这些现状问题一定程度降低了调度效率,导致整个系统调度滞后,特别是在早晚高峰时段产生借还空白期,严重影响用户的满意度,不利于系统的良性发展。
目前,关于公共自行车调度的研究已成为交通领域的研究热点之一。A. KALTENBRUNNER[1]等以自行车交通流为基础,对任一自行车服务网点的自行车数量进行提取预测,为动态调度提供了依据;M.BENCHIMOL[2]、刘登涛[3]等以运输费用最少为目标建立静态调度模型;R A.RUSSELL[4]、胡列格[5]等在考虑所需运输车辆数最少的基础上建立有时间窗的调度模型;柳祖鹏等[6]将货郎担问题运用到公共自行车的动态调度问题中来,提供了一种优化站间调度思路;董红召、吴满金、秦茜等[7-9]以最大化公共自行车用户的满意度为目标建立调度模型,并采用滚动时域调度算法进行求解,实现了公共自行车系统的动态调度。上述文献多根据用户满意度最大化或运输成本最小化两大目标建立动、静态优化调度模型,并针对求解算法做了一定探索。
但是,现有文献的研究多侧重于调度过程的实施环节,而忽略了需求预测环节,且优化模型在量化系统平均用户满意度时,没有考虑到各服务点间因需求差异从而对系统平均满意度的权重影响也有所不同。因此,考虑调度过程的各环节,笔者尝试探讨基于用户预约数据的高峰期调度需求预测,并建立最小化运输成本、最大化用户满意度的调度模型,优化调度路径,为有效解决高峰期公共自行车“借车难、还车难”问题提供参考。
1基于用户预约数据的高峰期调度需求预测
1.1采集并处理预约数据
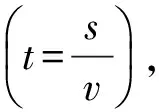
1.2读取并处理历史数据
首先系统读取后台历史记录数据,包括借车数据、还车数据以及对应的时间点,然后进行分类统计,区分工作日、周末以及节假日,剔除异常数据后,编成时间序列,最后综合长期趋势与季节变动等因素,运用SPSS中ARIMA模型对时间序列进行分析预测,得到下一个高峰期Δt时段内网点i的需求量预测值H(i,Δt)。
相比其他模型,ARIMA模型最明显的特点是考虑了预测对象由于季节周期性等因素引起的数据序列非平稳现象,通过差分运算、模型定阶等步骤使得预测值更精确。
1.3确定网点调度需求量
1) 整合预约数据值和根据历史数据求得的预测值,确定不同网点各时间段的预测需求量。
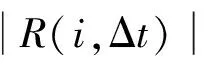
O(i,Δt)=R(i,Δt)×α
(1)
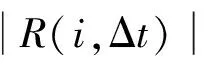
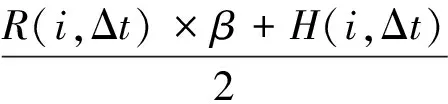
(2)
式中:O(i,Δt)为Δt时段内网点i的公共自行车车辆预测需求量(负值表示车桩需求量);α、β为未预约用户预留系数,初值可取1.1~1.2,随历史数据累计修正。
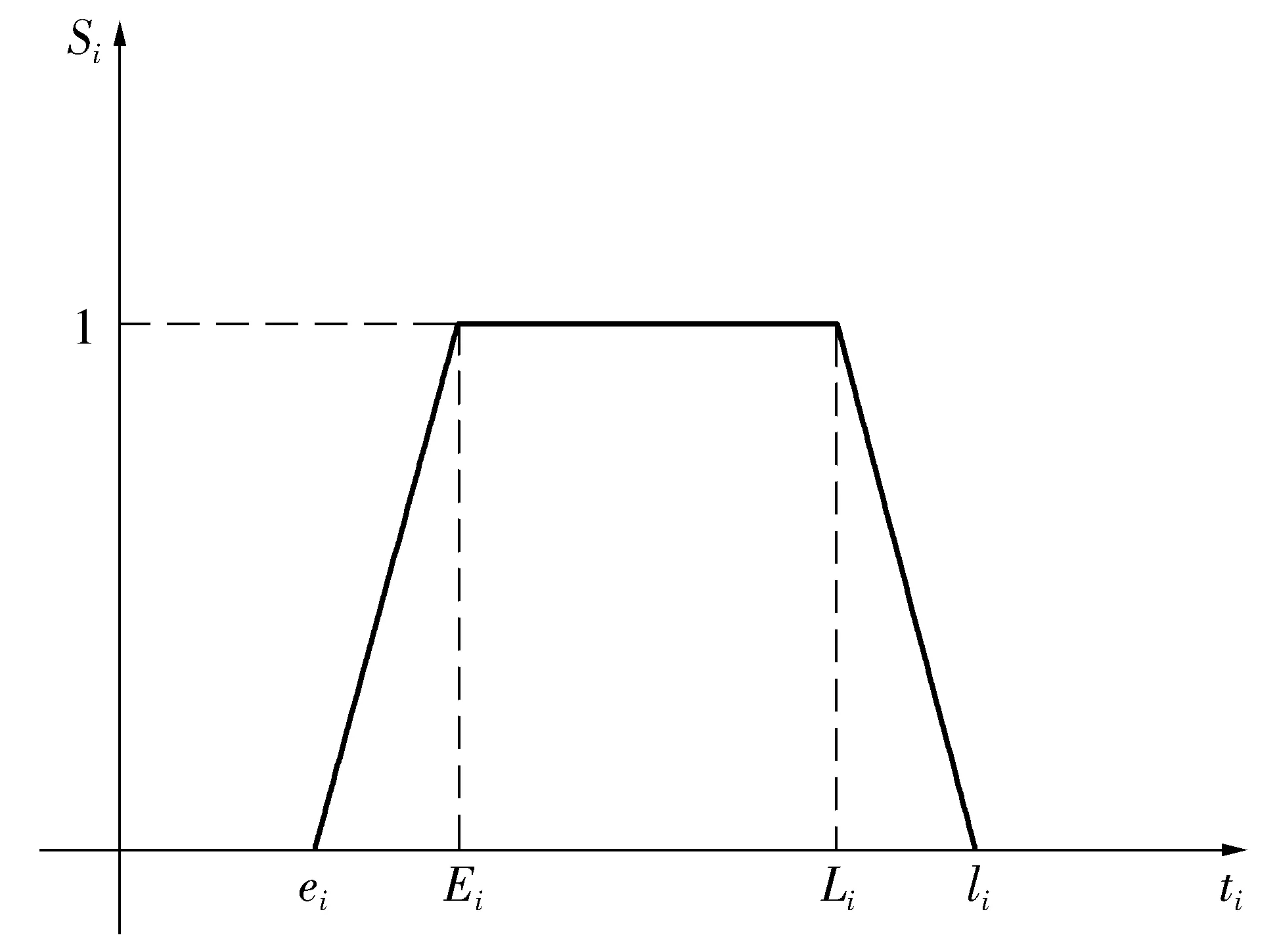
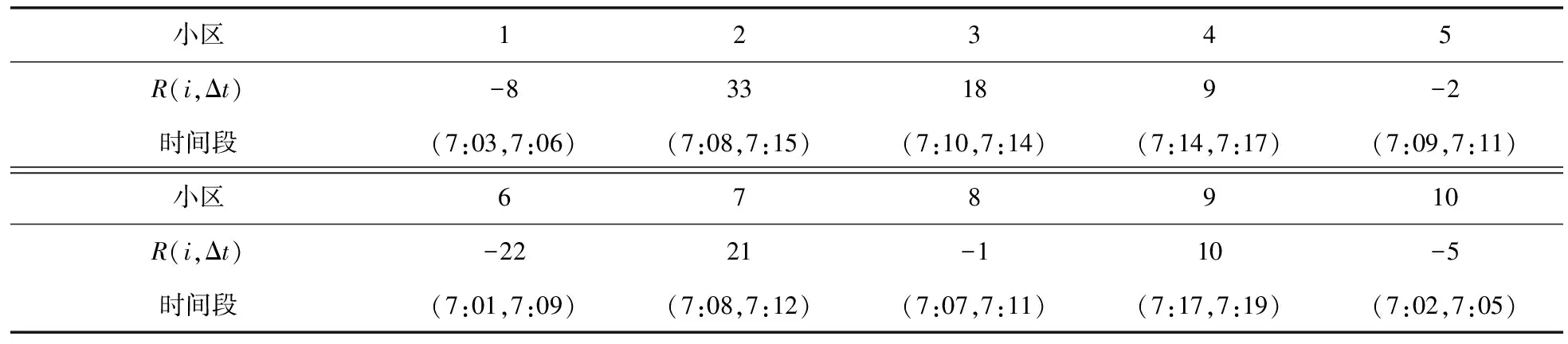
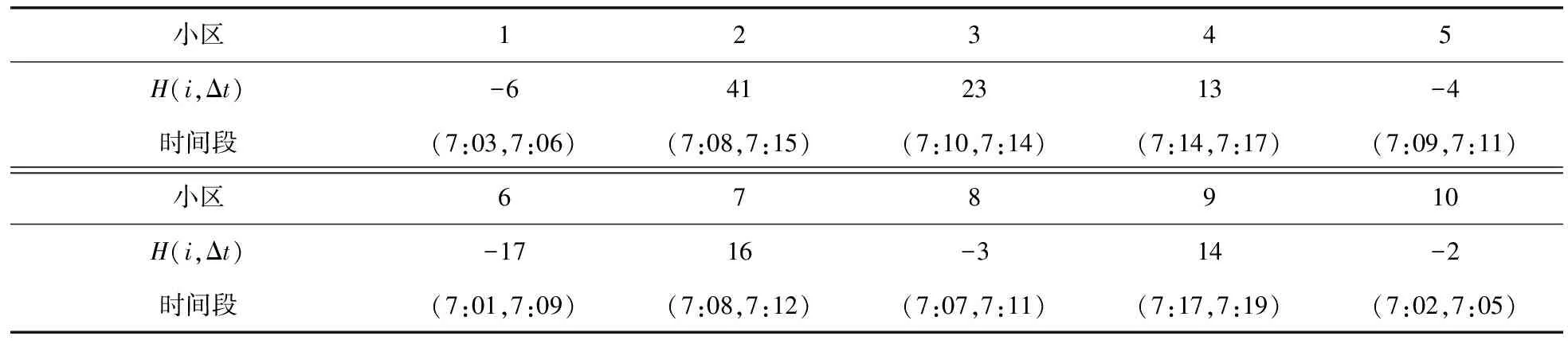
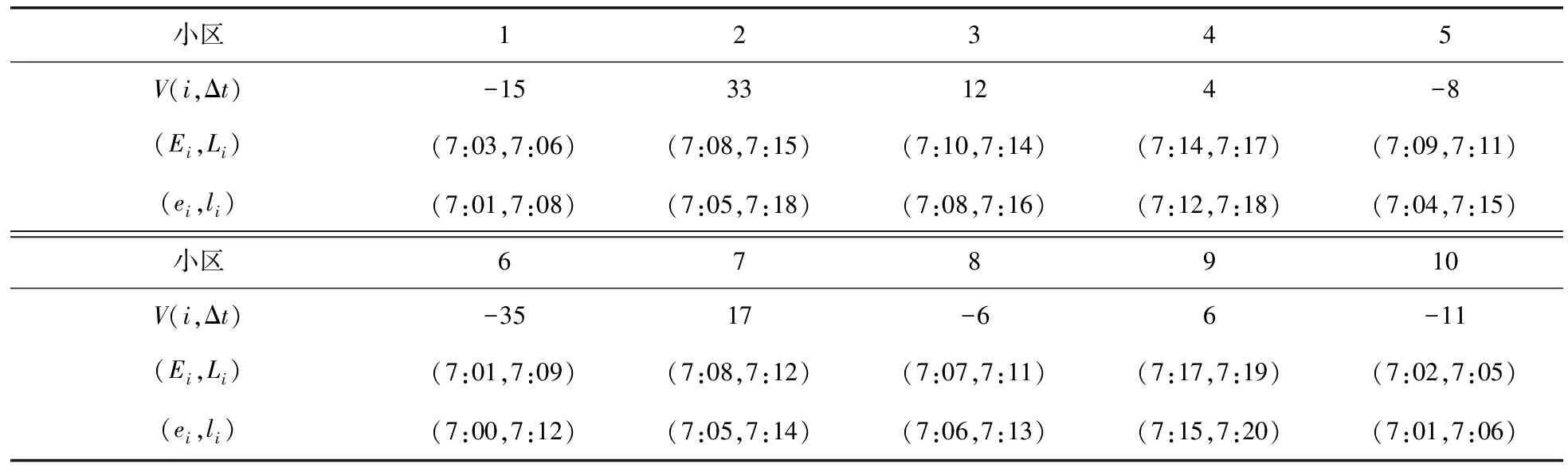
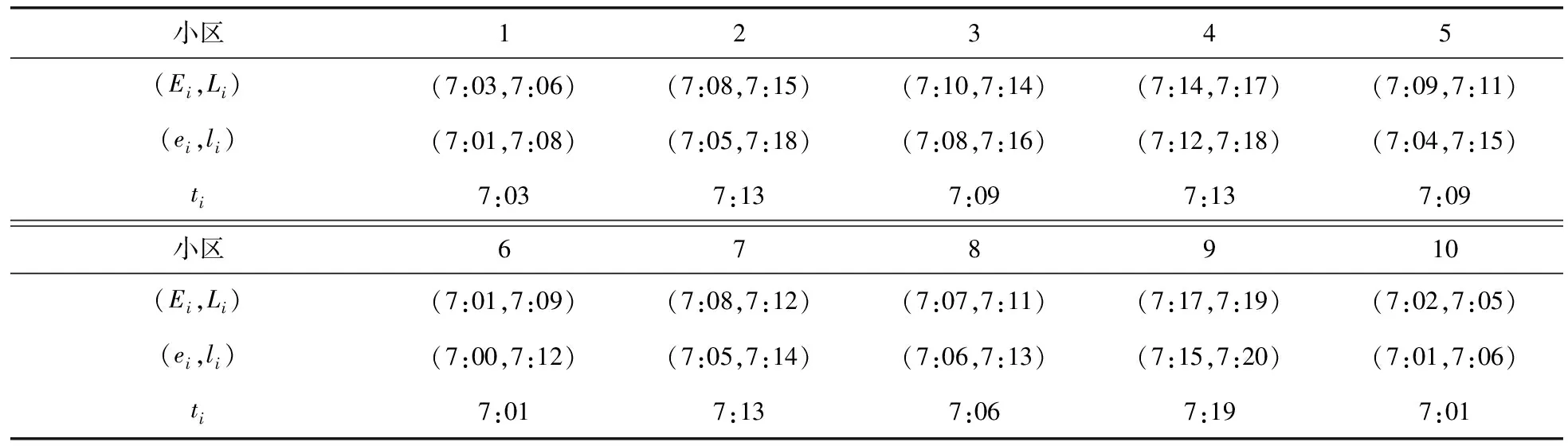
在方案使用初期,R(i,Δt) 2) 结合网点公共自行车存量,确定最终调度需求量。 V(i,Δt)=O(i,Δt)-Pi (3) 式中:V(i,Δt)为网点i在Δt时段的公共自行车车辆调度需求量(负值表示车桩需求量);Pi为各时间段开始前网点i的公共自行车数量。 2.1调度小区划分 城市公共自行车系统服务网点布局广、密度大,导致在运营过程中,面临调度路径复杂、随机误差大、时效性差等问题[10]。针对以上问题,笔者在充分分析各服务网点时空分布特性后,确立了两层分区调度方法,将高峰期借还特性相近且距离不大的服务网点划分为一个小区,每个小区的服务网点个数根据小区整体调度需求灵活设置,但一般不应大于6个。不同层面的调度策略有所差异,小区层面:建立以小区总体需求为基准的小区间软时间窗调度模型,最终确定调度方案;小区内部:根据小区内服务网点的位置和路径,采用最短路模型确定调度固定路线。笔者的研究重点是小区层面的调度。 2.2虚拟小区设置 由于调度模型是针对调度小区建立的,且受运输车辆的容量限制,难免会出现一个调度小区的调度需求量大于运输车辆的最大容量,为了解决这一困惑,笔者采取设置虚拟小区的方法,并假定虚拟小区的坐标信息与原小区的坐标信息一致,虚拟小区的调度需求量由原小区的调度需求量平均分配。 2.3服务满意度量化 公共自行车系统的运营效益,与服务质量有直接关系,而由调度服务时间决定的用户满意度是衡量服务质量的重要因素之一。用户的满意度一般通过借还车过程中的时间消耗值来量化,若在期望时间内完成借还车,则用户满意度最大,服务效果最好;若介于期望时间与可接受时间内完成,则用户满意度随着消耗时间的增加而降低;其它情况下,满意度为0,即用户不可接受,如图1。 图1用户满意度与时间的关系Fig.1Relationship between user satisfaction and time 假设运输车辆到达服务网点i的时刻为ti,则该服务网点的用户平均满意度Si(ti)表示如下: (4) 笔者重点考虑的是高峰期公共自行车系统的调度问题,用户对时间要求都比较高,但由于各服务点间需求存在一定差异,导致不同服务点对系统的平均满意度影响程度不一样,需求大的,其权重影响大,反之亦成立。因此,考虑到各服务点需求差异,系统的平均用户满意度则为: (5) 2.4参数说明 N:调度小区编号{0,1,2,…,n},其中0表示中心车场;M:虚拟小区编号{n+1,n+2,…,n+m};K:运输车辆{1,2,…,p}; i,j∈N∪M;k∈K; i∈N∪M;k∈K; dij:小区i到小区j的实际距离;qi:小区i的调度需求量,调入为正,调出为负;Q:运输车辆的最大载运量;Rqijk:运输车辆k从服务网点i到服务网点j车上载运量: (6) li:小区i可接受的最晚服务时间;ei:小区i可接受的最早服务时间;Li:小区i的期望最晚服务时间;Ei:小区i的期望最早服务时间;ti:运输车辆到达小区i的时间;tij:运输车辆从小区i到小区j的行驶时间;tui:运输车辆在小区i的装卸时间;P:权重系数,P1+P2+P3=1,具体数值根据系统测算需求而定;C0:单位运输车辆的固定成本;C1:运输车辆单位里程的成本费用;C2:满意度与成本换算系数,取值大小与系统平均满意度相关,同时受城市居民平均工资水平、公共自行车系统发展状况等多因素影响。 2.5调度模型建立 综上分析,考虑运营固定成本、行驶成本以及用户满意度,建立综合成本最小化的优化调度模型如下: (7) s.t. (8) (9) 0≤Rqijk-qj≤Q (10) (11) tj=ti+tui+tij (12) (13) 目标函数式(7)第1部分为固定成本,C0的取值与人工费用、车辆折旧费用以及其它固定费用等有关;第2部分为行驶成本,其值与单位油耗、实际行驶距离等有关;第3部分为系统总体满意度;约束条件式(8)表示运输车辆必须从中心车场出发并开始服务;式(9)表示完成调度任务后,运输车辆必须从最后一个服务点回到中心车场;式(10)表示运输车辆服务任一小区时,其原有载运量与该小区调度需求量之和不小于0且不大于运输车辆的最大载运量;式(11)表示任一调度小区至多由1辆运输车服务;式(12)表示到达下一服务网点的时刻由上一服务网点的开始服务时刻、服务时长以及两点间的行程时间决定;式(13)表示运输车辆服务完某一调度小区后,必须从该小区离开。 2.6算法设计 笔者将采用改进的遗传算法对调度模型进行求解。在调度优化问题上,遗传算法相对于其它算法,具有高效、实用性强、鲁棒性强等特点,其良好的全局搜索能力,可以快速地将解空间中的全体解搜索出,而不会陷入局部最优解的快速下降陷阱,并且它可以利用内在的并行性,方便进行分布式计算,加快了求解速度[11]。 针对文中的调度模型,算法设计步骤如下[12-14]: Step1染色体编码 遗传算法在进行搜索前,需选择适当的编码策略,将解数据表示成基因串结构数据。适合文中调度模型的编码方式是实数编码,将需要进行调度的小区用1、2、…、n、n+1、…、n+m表示,求得的解根据运输车辆最大载运量等约束条件分配给不同的车辆。 Step2生成初始种群 系统随机产生一系列初始串结构数据作为初始种群。初始种群的数目一般根据经验得到,一般情况下种群数量越大,生成的解效果越好,但同时也会降低求解速度,其取值通常在20~100之间,本次研究中,算例调度区域相对较小,我们确定初始种群数目为30。 Step3计算适应度值 适应度函数是用来判断群体中个体优劣程度的指标,其值越大,证明该个体相对更优。根据本文调度模型的特性,选取以下函数计算个体的适应度值。 (14) 式中:f(xi)为某个体(调度方案)的目标函数值,f(x)min为种群中所有个体(调度方案)目标函数的最小值。 Step4选择算子 笔者采用最经典的选择方法——轮盘赌算法,该算法选择个体的概率与其适应度值有关,假设种群个体数量为N,则个体i被选中的概率为: (15) Step5交叉操作 从种群中随机选取两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而得到新的优秀个体。本文假设交叉概率Pc为0.85,采用顺序交叉法对个体进行交叉操作。 Step6变异操作 变异操作是为了保持种群的多样性,本文假设变异概率Pm为0.005,采用2-Opt算法对个体进行变异操作。 Step7终止运算 若进化代数大于预设的遗传代数,或算法在连续进化一定代数后,个体的适应度值没有明显改进,则终止运算。 3.1前期准备 笔者选取了广州市某区域的公共自行车系统作为调度研究区域。区域内包含中心车场1个,各类站点共27个,其中公建类11个,公交站点类6个,交通枢纽类2个,住宅类7个,休闲类1个,涵盖类别相对全面。 根据各服务网点坐标、高峰期借还数据进行聚类分析,将研究区域分成10个小区,其中1、5、6小区以公建类为主,2、3、9小区为住宅类,4以交通枢纽类为主,7、8为公交站点类,10为休闲类,各小区的基本信息、各时段的需求预约量以及根据历史数据求得的各时段需求预测值分别如表1、表2、表3。 整合表2与表3,可以确定需要在不同的时间段,对10个调度小区,共147辆公共自行车进行调度服务,具体如表4。 表1不同调度小区基本信息Table 1Basic information of different service areas 表2不同调度小区各时间段的预约量Table 2Reservations of different service areas in each time section 表3不同调度小区各时间段的预测值Table 3Prediction values of different service areas in each time section 表4不同调度小区各时间段的调度需求量Table 4Scheduling demand of different service areas in each time section 3.2结果分析 分别使用人工经验方法和文中的优化算法对上述案例进行求解,结果如表5、表6。对比结果显示,优化后调度方案的综合成本为42.57元,比优化前调度方案的综合成本节约了8.45元,即综合成本降低了16.6%。此外,从表6可以发现,优化后,运输车辆到达各服务小区开始服务的时刻均在用户可接受的时间段内,其中小区1、2、5、6处在用户期望服务的时间段内;换算成满意度后,除小区8和10外,其它小区的用户满意度均在0.5以上,且小区1、2、5、6的满意度值达到1,系统平均满意度值由优化前的0.620 5提升到优化后的0.798 5,提升幅度为28.7%,用户总体较为满意。 由于本算例选取的研究区域面积不到0.5 km2,是广州市某片区总规划用地面积的1/13,因此测算结果中综合成本的绝对数值较小,倘若将此优化调度模型应用至片区乃至全市整个公共自行车系统,其优化效果将更明显。 表5优化前后调度方案的对比分析Table 5Contrastive analysis of dispatching schemes before and after optimization 表6优化后运输车到达各服务点的实际时间Table 6Actual service time which the transport vehicles use to arrive at each service point after optimization 在城市公共自行车“借车难、还车难”问题愈发突出的大背景下,笔者针对现状城市公共自行车调度对系统性考虑不足、路径未经优化等问题,以及高峰期对用户实际需求缺乏预判使得调度滞后、用户整体满意度低的情况,提出基于用户预约数据的高峰期公共自行车需求预测方法,利用互联网平台以及后台历史记录数据,提前预测用户实际需求,然后在量化平均用户满意度的基础上,建立最小化运输成本、最大化用户满意度的公共自行车调度模型,并采用遗传算法进行求解。算例结果表明:该算法可以有效地减少系统综合成本,提升用户满意度,对城市公共自行车优化调度具有一定的指导作用。 准确预测用户需求以便更有针对性的制定调度计划,可以改善用户体验,提升用户满意度。考虑天气、空气质量等影响用户选择自行车出行的指标,可以使需求预测模型更贴近实际,是下一步研究的方向之一。 [1] KALTENBRUNNER A,MEZA R,GRIVOLLA J.Urban cycles and mobility patterns:exploring and predicting trends in a bicycle-based public transport system[J].PervasiveandMobileComputing,2010,6(4):455-466. [2] BENCHIMOL M,BENCHIMOL P,CHAPPERT B,et al.Balancing the stations of a self-service“Bike Hire”system[J].RAIRO-OperationsResearch,2011,45(1):37-61. [3] 刘登涛,方文道,章坚民,郭明泽.公共自行车交通系统调度算法[J].计算机系统应用,2011,20(9):112-116. LIU Dengtao,FANG Wendao,ZHANG Jianmin,GUO Mingze.Scheduling algorithm for public bicycle system[J].ComputerSystems&Applications,2011,20(9):112-116. [4] RUSSELL R A.Hybrid Heuristics for the vehicle routing problem with time windows[J].Transportation Science,1995,29(2):156-166. [5] 胡列格,夏云,王佳,等.城市公共自行车高峰期需求不均衡的调度优化研究[J].铁道科学与工程学报,2015 (2):441-448. HU Liege,XIA Yun,WANG Jia,et al.Scheduling optimization research on demand imbalance of urban public bicycles during peak period[J].JournalofRailwayScienceandEngineering,2015(2):441-448. [6] 柳祖鹏,丁卫东,程逸旻.公共自行车系统站点间调度优化研究[J].城市公共交通,2011(1):39-42. LIU Zupeng,DING Weidong,CHENG Yimin.Research of optimal scheduling between stations for public bicycle system[J].UrbanPublicTransport,2011(1):39-42. [7] 董红召,赵敬洋,郭海峰,等.公共慢行系统的动态调度建模与滚动时域调度算法研究[J].公路工程,2009,34(6):68-71. DONG Hongzhao,ZHAO Jingyang,GUO Haifeng,et al.Research on the dynamic model and rolling horizon scheduling algorithm for public-use bicycle vehicle scheduling problem[J].HighwayEngineering,2009,34(6):68-71. [8] 吴满金,董红召,刘东旭,等.公共自行车多目标动态调度建模与算法研究[J].机电工程,2015,32(7):1006-1010. WU Manjin,DONG Hongzhao,LIU Dongxu,et al.Research on the dynamic model with multi-objective and algorithm for public rebalance problem[J].JournalofMechanical&ElectricalEngineering, 2015,32(7):1006-1010. [9] 秦茜.公共自行车租赁系统调度问题研究[D].北京:北京交通大学,2013. QIN Xi.TheResearchonRepositioninginaBbike-sharingSystem[D].Beijing:Beijing Jiaotong University,2013. [10] CHEMLA D,MEUNIER F,CALVO R W.Bike sharing system solving the static rebalancing problem[J].DiscreteOptimization,2013,10(2):120-146. [11] GASPERO L D,RENDL A,URLI T.Constraint based approaches for balancing bike sharing systems[J].SpringerBerlinHeidelberg,2013,8124:758-773. [12] 史彩霞.公共自行车系统运行数据时空分析及智能调度系统的研究[D].杭州:浙江工业大学,2012. SHI Caixia.AnalysisonRunningDataandResearchintheIntelligentVehicleSchedulingforPublicBicycleSystem[D].Hangzhou:Zhejiang University of Technology,2012. [13] 李锦霞.公共自行车调度优化研究[D].长沙:长沙理工大学,2013. LIN Jinxia.TheSchedulingOptimizationStudyofUrbanPublicBicycle[D].Changsha:Changsha University of Science & Technology,2013. [14] 管娜娜.公共自行车调度路径优化问题研究[D].成都:西南交通大学,2015. GUAN Nana.ResearchonPublicBicycleRoutingandSchedulingOptimization[D].Chengdu:Southwest Jiaotong University,2015. (责任编辑:朱汉容) Scheduling of Public Bicycle during Peak Period Based on the Customer Reservation Data JIN Wenzhou,YE Qinhai,HAO Xiaoni (School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640,Guangdong,P.R.China) The issues of scheduling delay and low customer satisfaction caused by the lack of demand forecast during peak period and the concept of systematic scheduling in the public bicycle system were analyzed.The quantization method of scheduling demand forecast and system average satisfaction of the public bicycle during peak period was discussed; the optimal routing of the public bicycle scheduling was also analyzed.According to the analysis on the scheduling demand forecast model based on the customer reservation data during peak period,the optimal scheduling model to minimize the comprehensive scheduling costs with considering the customer satisfaction level was established,and then an improved Genetic Algorithm was adopted to solve the proposed model.Finally,a case study of the public bicycle system at certain area in Guangzhou was cited to verify the proposed model.Research results show that,compared with the conventional scheduling plan,the comprehensive cost of the proposed model is reduced by 16.6% and the system average customer satisfaction is improved by 28.7%. traffic and transportation engineering; public bicycle; demand forecast; system average satisfaction; optimal scheduling; genetic algorithm U492.2+2 A 1674-0696(2017)10-091-06 2016-07-25; 2016-08-29 国家自然科学基金项目(61473122);中央高校基本科研业务费专项资金项目(2015ZM124) 靳文舟(1960—),男,吉林四平人,教授,博士,主要从事交通运输规划与管理研究。E-mail:ctwzhjin@scut.edu.cn。 10.3969/j.issn.1674-0696.2017.10.152公共自行车调度模型建立
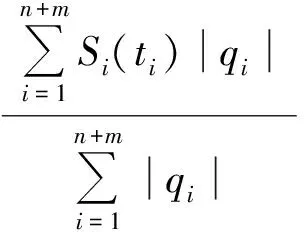
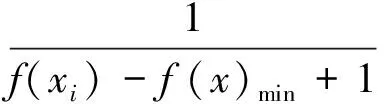
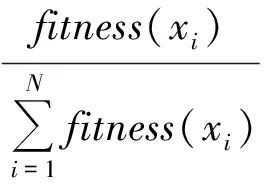
3实例分析
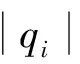


4结语

