列车运行调度MLD模型

王宏刚，马明君

(重庆交通大学 信息科学与工程学院，重庆 400074)

列车运行调度MLD模型

王宏刚，马明君

(重庆交通大学 信息科学与工程学院，重庆 400074)

通过对影响列车运行状态的事件进行分析，指出各类事件对列车状态的影响本质上是改变列车的加速度。采用MLD建模理论建立了列车运行调度模型，该模型将连续行为和离散行为统一在一个框架中并考虑了停站时间、安全距离等约束。以6站5区间的调度区段为例，对模型进行了仿真研究。针对施加干扰后列车发生的晚点的情况，采用压缩列车停站时间和区间运行时间的方法对晚点的列车进行调整，最终列车恢复了正点运行。仿真结果证明了模型的有效性和正确性。

交通运输工程；列车调度；混合逻辑动态系统；仿真；调整

列车连续运行过程和离散变化过程组成了列车运行调度系统，是典型的混杂动态系统。众多学者采用混杂动态系统理论(hybrid dynamic system，HDS)对列车运行调度问题进行了研究。

周磊山等[1]从离散事件角度描述了列车调度问题，并采用离散事件动态系统建模理论建立列车运行调整的系统状态转移方程，并对其进行了求解。王宏刚[2]认为列车运行调度问题的实质是通过采用可控事件(相应的调度命令)来消除或降低不可控事件(不可预测干扰)对列车正常运行造成的影响，从而恢复列车正常运行，并采用Petri网建立了列车运行调度模型。叶阳东等[3]采用Petri网对列车运行过程进行了建模和仿真，利用连续库所变迁描述系统中连续变量的变化过程，并采用关联方程表示连续变量属性的变化，仿真结果证明了模型有效性。上述研究成果偏重于从离散事件角度对列车运行调度系统进行了建模和研究。

根据王宏刚[2]的分析结果，王村等[4]在假设事件对列车运行状态影响体现在对列车运行速度改变的基础上，采用混合逻辑动态系统(mixed logic dynamic，MLD)理论初步对列车运行调度模型进行了研究。该研究成果有一定的借鉴性，但在建立模型时假设速度若发生跃变，则会产生较大误差。

为与实际情况相符，减少误差，笔者在王村等[4]研究基础上，认定干扰事件对列车运行状态的影响是对列车运行加速度的影响，采用MLD理论建立列车运行调度系统模型，使得模型更接近列车的实际运行状况，并进行了仿真。

1MLD建模理论

MLD建模理论是混杂动态系统理论中的一种建模方法。该建模理论充分考虑了系统的定性知识和定量知识，把对象启发式知识、逻辑法则和需要满足的约束条件通过逻辑命题转换成线性不等式，将混杂系统中的连续部分和离散部分统一在一个框架中。

笔者对MLD建模步骤做简单介绍[5-7]：

1) 对系统进行分析，建立能够描述系统在各种不同运动状态下的数学模型；

2) 对系统的定性知识和逻辑约束建立逻辑命题，并将其转换成线性不等式；

3) 根据离散变量和连续变量的耦合关系引入逻辑变量、辅助变量，并结合2)中的线性不等式转换方式，将系统中的离散事件和连续变量整合在同一个框架下，建立MLD模型，如式(1)。

(1)

式中：x(t)为系统状态；A、B、C、D、E为常系数矩阵；y(t)为系统输出；u(t)为系统输入变量；δ(t)为逻辑变量；z(t)为辅助连续变量。

2列车运行调度问题分析

在理想状态下，按照列车运行计划图，列车准点从车站发车，加速到区间速度后保持匀速运行，即将到达前方车站时，列车制动减速运行，直至速度降为0时停车，一直重复该运行过程。根据物理学相关知识，列车在区间的运行状态包含静止、加加速、匀速和匀减速这4种状态。正常情况下，改变列车运行状态的事件包括列车发车、列车进站、列车停车、达到区间速度这4类事件。根据列车运行图可事先计算出这些事件发生的时刻。

由于列车运行跨度大，经常会受到自然环境影响，如强侧向风、暴风雪、泥石流等，同时这些事件发生随机性比较强，且不可预测，这类事件在下文中统称干扰事件。这些情况一旦发生，列车通常需要降速运行甚至临时停车，导致列车发生晚点。干扰事件发生时刻的不确定性导致列车运行状态非正常改变时刻也具有不确定性，即无法事前计算出列车的加速、减速、匀速和停车时刻。

干扰事件消失或减弱后，调度员需要制定出调整计划来恢复晚点列车正点运行或者尽可能的缩小列车实际运行情况与运行图之间的偏差。即在保证列车运行安全的前提下，通过压缩列车在车站的停车时间、区间运行时分等手段来恢复列车运行秩序。就其本质而言，压缩列车停站时间和区间运行时分都是在某个时刻改变列车运行加速度达到改变列车运行状态的目的。

如上所述，干扰事件的发生往往会导致列车实际运行偏离运行图。调度员结合列车运行实际情况和相应的约束条件，确定列车运行状态发生变化的时刻，来实现列车恢复正点运行的目的。笔者根据此思想，采用MLD建模理论建立列车运行调度的模型。

3列车运行调度MLD模型

3.1模型假设

依据实际情况，笔者在建模时做如下两种假设。

3.1.1不会发生极端情况

列车在实际运行中，可能会遇到极端情况，如隧道垮塌、线路异常等。在此极端情况下，全线停车是唯一安全可靠的调度策略。这种情况难以用模型描述，建模时不予考虑。

3.1.2列车加速度为恒值

列车运行加速度跟列车的质量、载客量、牵引性能、制动性能以及线路等因素息息相关。为简化计算，笔者假设列车的加速度a为恒定。当a>0时，列车为匀加速状态；当a<0时，列车为匀减速状态；当a=0时，列车在区间匀速运行或在车站停车。

基于以上假设，列车i运行的空间状态方程如式(2)：

(2)

式中：T为采样间隔时间；ai(k)为列车i在k时刻的加速度；vi(k)为列车i在k时刻的速度；si(k)为列车i在k时刻的位置。

3.2列车运行调度的MLD模型

式(2)描述了列车i正常运行情况。引入逻辑变量ri(k)∈{0，1}，ri(k)=1表示在k时刻向列车i的添加干扰事件，此时列车的运行速度不得大于vg，此时列车i的空间状态方程如式(3)：

(3)

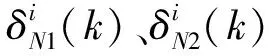
(4)

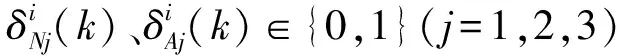
(5)

根据式(5)，式(4)可写成：

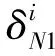
(6)

将式(6)代入式(4)，列车i的空间状态方程如式(7)：

(7)

根据相关规定，列车发车时间不早于运行图规定的发车时间，即调度员对车站r内的列车i下达发车命令时刻kT必须满足：

(8)

式中：tir为列车i在车站r的计划发车时刻；ξ为松弛变量。

根据列车在车站停站时间不得小于最短停站时间，有式(9)：

(kird-kira)T≥τir

(9)

式中：列车i在车站r出站时刻为kirdT；到达车站r的时刻为kiraT；τir为列车i在车站r的最短停车时间。

列车i在区间的运行速度vi(k)满足式(10)：

vi(k)≤vM

(10)

式中：vM为区间规定的最高速度。

设列车i和列车j为同方向的相邻列车，k时刻在同一区间追踪运行。区间的起始位置和终止位置分别为yr-1、yr。列车i在k时刻的位置为si(k)，列车j在k时刻的位置为sj(k)，则相邻列车之间的距离需满足式(11)：

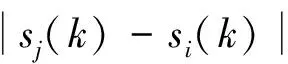
si(k)、sj(k)∈[yr-1，yr]

(11)

式中：la为同方向相邻列车的最小安全距离。

式(5)～式(11)构成对列车i的调度系统模型。其中：式(11)为列车的状态方程；式(5)为引入离散变量的约束条件；式(8)～(11)为规定的约束条件。

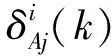
4仿真

4.1实例

通常情况下，复线铁路的双向运行列车在区间运行时互不干扰，即使在进行出入站作业时也很少占用对向列车的进路，因此在仿真时只考虑一个方向的运行列车。以6个车站5个区间的调度区段为例，线路示意如图1。

图1仿真线路示意Fig.1Diagram of simulation railway line

图1中：Si(i=1，2，…，6)表示车站，下角标为车站位置(单位：m)；qj(i=1，2，…，5)表示相应的区间。

列车的参数如表1。列车在中间站S2、S3、S4和S5最小停车时间如表2。

表1列车参数Table 1Parameters of trains

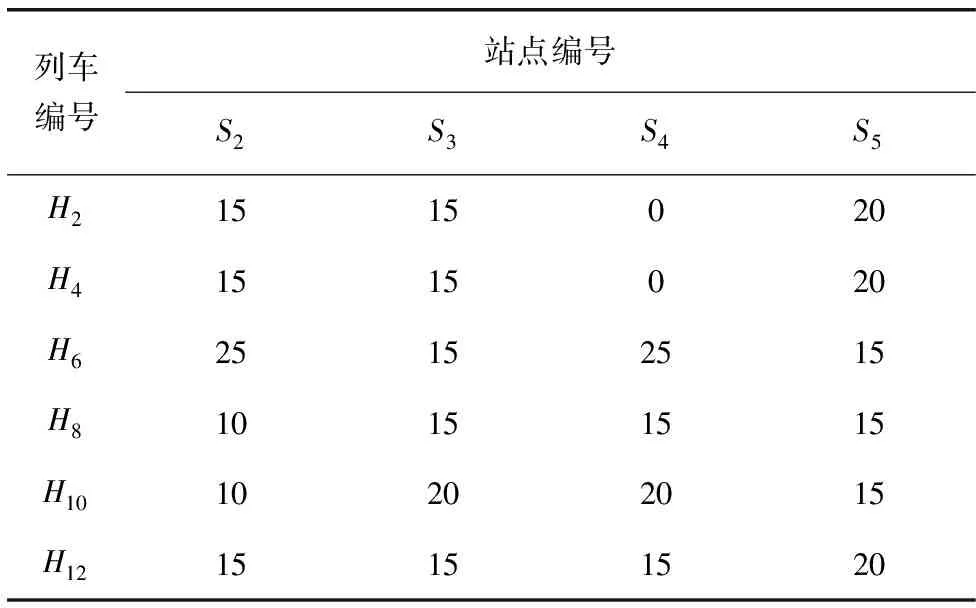
表2列车停靠时间Table 2Train’s dwell time s

仿真时所采用的列车运行计划如图2。

4.2仿真结果

仿真时，在400～1 800 m处施加干扰，干扰开始时刻是第100 s，持续时间200 s。为安全起见，进入干扰区间H8、H10和H12的列车以速度vg匀速运行，直至驶出干扰区间。干扰导致列车H8、H10和H12在到达车站S2时晚点。以列车H10为例，其速度变化曲线和调度命令如图3。

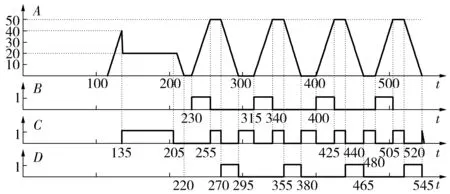
图3调整过程示意Fig.3Diagram of adjusting process

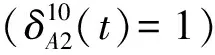
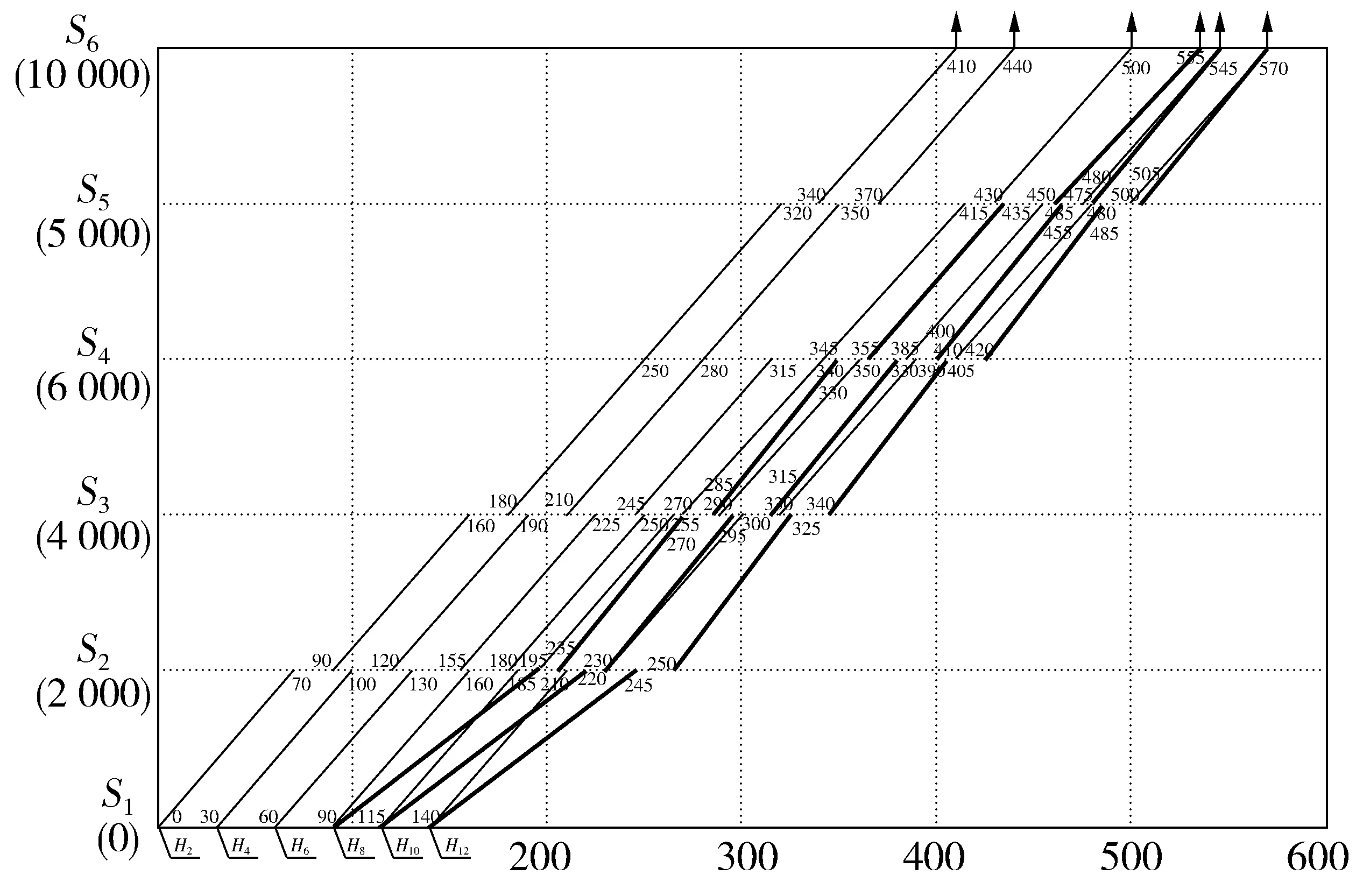
图4调整结果Fig.4Diagram of adjustment results

5结语

列车运行调度问题本质是在保证列车安全的前提下，在某时刻改变列车加速度即列车运行状态来消除或降低干扰因素造成的列车晚点，保证列车按照运行计划或尽量按照运行计划行驶。

在此基础上，笔者采用MLD建模理论建立了列车运行调度的模型，建模时考虑了列车的停站时间约束、发车时间约束以及区间追踪约束等条件。最后以6站5区间的调度区段为例对模型进行了仿真。仿真结果说明了模型的有效性。

[1] 周磊山，秦作睿.列车运行计划与调整的通用算法及其计算机实现[J].铁道学报，1994，16(3)：56-65.

ZHOU Leishan，QIN Zuorui.General algorithm and its realization on computer for the train operation adjustment system[J].JournaloftheChinaRailwaySociety，1994，16(3)：56-65.

[2] 王宏刚.复线列车运行调度的层次Petri模型及仿真[J].系统仿真学报，2011，23(12)：2793-2804.

WANG Honggang.Hierarchical Petri net model and simulation for train traffic control on double railway[J].JournalofSystemSimulation，2011，23(12)： 2793-2804.

[3] 叶阳东，程少芬，王旭，等.基于一种混合Petri网的列车运行系统的建模与分析[J].铁道学报，2009，31(5)：42-49.

YE Yangdong，CHENG Shaofen，WANG Xu，et al.Modeling and analyzing of train operation systems based on a kind of hybrid Petri net[J].JournaloftheChinaRailwaySociety，2009，31(5)： 42-49.

[4] 王村，王宏刚.基于混合逻辑动态的列车运行调度模型[J].工业控制计算机，2011，24(5)：52-55.

WANG Cun，WANG Honggang.Train traffic control model based on mixed logic dynamic[J].IndustrialControlComputer，2011，24(5)： 52-55.

[5] BEMPORAD A，MORARI M.Control of systems integrating logic，dynamic and constraints[J].Automatic，1999，35(3)： 407-427.

[6] 李秀改，高东杰，王宇红.基于混合逻辑动态模型的混杂系统预测控制[J].控制与决策，2002，17(3)：315-319.

LI Xiugai，GAO Dongjie，WANG Yuhong.Predictive control for hybrid system based on mixed logic dynamic model[J].ControlandDecision，2002，17(3)： 315-319.

[7] WANG Yuhong，ZHAO Xu.Improvement of optimal algorithm for hybrid system based on MLD model[C]//CCDC’09Proceedingsofthe21stAnnualInternationalConferenceonChineseControlandDecisionConference.NJ，USA： IEEE Press，2009： 4600-4604.

[8] HIRAGURI S，HIRAO Y，WATANABE I，et al.Advanced train and traffic control based on prediction of train movement[J].JSMEInternationalJournalSeriesC，2004，47(2)： 523-528.

[9] TÖMQUIST J.Computer-based decision support for railway traffic scheduling and dispatching： A review of models and algorithms[C]//5thWorkshoponAlgorithmicMethodsandModelsforOptimizationofRailways.Dagstuhl，Germany，2006，1-23.

[10] Francesco Corman，Andrea D’Ariano，Ingo A.Hansen，et al.Dispatching trains during seriously disrupted traffic situations[C]//2011InternationalConferenceonNetworking，SensingandControl.Delft，the Netherlands，2011，323-328.

(责任编辑：刘韬)

MLD Model of Train Traffic Control

WANG Honggang，MA Mingjun

(School of Information Science & Engineering，Chongqing Jiaotong University，Chongqing 400074，P.R.China)

Through analyzing the events affecting train operation status，it was pointed out that the essence of the effect imposed on trains by various events was to change train’s acceleration.Using the mixed logic dynamic system theory，the train traffic control model was established，which put the continuous and discrete behaviors into a unified framework and considered the constraints，such as the minimal dwell time and safe distance.A dispatch section including 6 stations and 5 sections was used to carry out the simulation study of the proposed model.For train’s delays resulting from the imposed disturbances in simulation，the method of compressing the dwell time and the interval running time in sections was used to adjust the delayed train，which eventually restored the train’s punctual operation.The validity and correctness of the proposed model is verified by simulation results.

traffic and transportation engineering; train control; mixed logic dynamic system; simulation; adjustment

U284.59

A

1674-0696(2017)10-107-05

2015-11-20；

2016-11-17

重庆市自然科学基金项目(cstc2012jjA40065)

王宏刚(1970—)，男，山西临猗人，教授，博士，主要从事列车运行调度和混杂系统理论方面的研究。E-mail： wanghg70@aliyun.com。

马明君(1990—)，男，湖北十堰人，硕士研究生，主要从事列车运行调度理论与混杂系统方面的研究。E-mail： 827876259@qq.com。

10.3969/j.issn.1674-0696.2017.10.18