基于参数优化的支撑矢量机及其在故障诊断中的应用

陈虎

(重庆市轨道交通(集团)有限公司，重庆400042)

基于参数优化的支撑矢量机及其在故障诊断中的应用

陈虎

(重庆市轨道交通(集团)有限公司，重庆400042)

为了有效的诊断出设备的故障，给出了一种基于参数优化的支撑矢量机算法。该算法首先引入免疫克隆选择机制，以两个十进制数表示一个抗体来构建抗体群，以漏报率为基础构造亲和度函数，实现支撑矢量机参数的优化。然后使用优化后的参数构造支撑矢量分类器对设备数据进行分类检测。通过在汽轮发电机组的数据集上进行仿真验证，实验结果表明，该算法相对传统的支撑矢量机算法不会显著增加训练时间，并且能够有效提高检测率和降低误检率。

机电工程；故障诊断；支撑矢量机；参数优化；免疫克隆算法

故障诊断是工程技术领域一个重要的问题。如何及时有效地检测出故障对保证设备正常运行和业务的连续开展有关键作用。近年来故障诊断方法研究也成为学术及工程技术等领域的热点，相关学者提出了许多可用的方法，如神经网络[1]、支撑矢量机[2]、独立分量分析[3]及各种组合算法[4-7]的使用，都取得了一定的效果。

作为一个好的分类器，支撑矢量机相对于其它的分类算法具有更高的推广能力。然而，支撑矢量机在实际的应用中有一个显著的问题是如何选择合适的参数来构造一个有效的分类器并使其具有最好的性能。一般而言，支撑矢量机中的参数选择主要借助于专家的实践经验，但这种参数的确定方法在实践中往往不能够获得最优的分类器，从而影响了支撑矢量机的分类效果。

基于上述原因，笔者引入了免疫克隆选择算法，并将其用于优化支撑矢量机的参数。为验证优化后的分类效果，笔者将优化后的分类器用于对汽轮发电机组的故障进行诊断分类，提出了一种基于参数优化的支撑矢量机故障诊断方法。

笔者的内容组织如下：首先对文中用到的基本技术，既支撑矢量机和免疫克隆选择算法[8]进行介绍；并提出了一种基于免疫克隆选择优化的支撑矢量分类器；最后描述了其仿真结果并对仿真结果进行了分析。

1技术背景

1.1支撑矢量机(support vector machines，SVM)

支持矢量机是当前比较流行的一种小样本分类算法，它能够利用少量的样本进行训练学习，从而得到比较理想的分类效果。其基础理论是利用了统计学中的VC维理论[9]，并引入了结构风险最小化原理。利用少量样本，对SVM进行训练，得到一个相对最佳的超平面，并通过该超平面可实现数据的分类。

SVM主要用来解决二类可分的问题，基本目标就是找到一个最佳的超平面，它可用于线性可分与线性不可分两种场景。在线性可分的情况下，可将寻找最佳超平的问题转化为求解一个最优(凸规划)的问题。而在非线性可分的问题中，则需要使用非线性映射算法将低维线性不可分的问题转化为高维特征空间中线性可分的问题，因此它具有较好的推广能力。同时它基于Vapnik结构风险最小化原则，具有较好的泛化能力。基于SVM的非线性问题的分类算法如下。

假定：x为k维向量，并给定m个样本集分别为(x1，y1)，…，(xm，ym)，x∈Rk，y∈{-1，1}。则有如下超平面：w·x+b=0。

若上述超平面可以将样本分隔为两类，则构造最佳超平面的问题，就可以转化为寻找向量w0和常数b0的问题。由此可给出如下的构造，即使向量w0具有最小的范数，并且满足约束条件：

yi[(xi·w0)+b0]≥1

(1)

引入松弛变量ζi≥0，问题转化为最小化下列二次优化问题，约束条件如式(1)：

(2)

式中：C为正常数，代表对错分的惩罚因子。

在对偶空间求解这个二次优化问题，由此问题转化为

(3)

C≥ai≥0，i=1，…，m

得到解

(4)

最优解w0和b0必须满足Kuhn-Tucker条件，由此得

yi(xi·w0+b0)=1

(5)

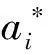
(6)

根据Mercer定理，任何满足半正定的函数都可以作为核函数，而对于满足条件的核函数，都会对应一个特征空间中的内积。因此在最佳超平面上选择合适的内积函数，就可实现线性不可分问题到线性可分问题的映射。由此非线性支持矢量机的优化问题如式(6)。

非线性支持矢量机的判决函数如下：

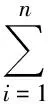
(7)

1.2免疫克隆选择算法

受生物免疫系统克隆选择机理的启发，研究者设计了一种新的智能优化算法，既免疫克隆选择算法(immune clone selection algorithm，ICSA)。该算法可很好的结合先验知识，并引入了生物免疫系统中的自适应能力，所以在信息处理方面具有很强的鲁棒性，在进行优化搜索时可收敛到全局最优。

作为一种新提出的全局最优搜索算法，该算法在实现上能够兼顾全部和局部搜索。在搜索过程中能够构造记忆单元，记忆最优解的群体，从而比单纯的遗传算法具有更好的收敛性。

克隆算法利用记忆单元和将变异算子升级为主要算法，可以在候选解中构造一个变异解的群体，使得搜索范围更大，从而使得抗体群的多样性大大增加，由此可以保证算法能够以概率1收敛到最优解。免疫克隆算法的基本步骤如下：

步骤1：初始化抗体群，设定算法的参数并计算初始亲和度；

步骤2：根据亲和度和抗体克隆规模，进行克隆操作、免疫基因操作、克隆选择，生成新的抗体群；

步骤3：计算新的亲和度；

步骤4：若满足结束条件，则退出；否则，跳转到步骤2。

2参数优化的支撑矢量机

在使用支撑矢量机进行分类的过程中，其参数的选择对分类和检测的性能有很大的影响，因此笔者介绍使用免疫克隆选择算法进行支撑矢量机参数优化的基本思路。

2.1支撑矢量机中的主要参数

在式(2)中：C为一个正常数，它控制对错分样本惩罚的程度。若C太小，则惩罚力度不够，会导致算法对数据的拟合不够；若C太大，则会导致算法的过度拟合。ξ为算法引入的一个正的松弛因子，代表允许错分样本的存在，它会影响到分类器所产生的支撑矢量的个数，从而进一步影响到分类器的最大总误差。如果ξ太大，则获得支撑矢量的个数就会减少，使得分类的误差增加，反之依然。

而核函数中的参数则反应了训练数据的特征，对整体的分类性能有很大影响，因此也需慎重选择。在支撑矢量机中经常用到的核函数是线性核函数、多项式核函数和RBF核函数。笔者选择RBF核函数作为支撑矢量机的核，原因是虽然线性核函数，参数比较少，相对速度快，但对非线性问题无能为力。RBF核函数与多项式核函数相比，RBF需要确定的参数要少，复杂度相应较低。此外，需要考虑的是：多项式核函数存在当阶数较高时，核矩阵元素值过大或过小的问题，而RBF则不会出现此类问题。

RBF核函数的形式如式(8)：

(8)

式中：σ为函数的宽度参数，用于控制函数的径向范围。

2.2编码方案

进行优化的第一步就是对需要优化的参数确定合适的编码方案，能够以指定长度的数字串来标示这些参数在问题空间中的所有取值情况。笔者考虑到所要解决问题的实际情况，以十进制的编码方式来构造抗体种群，基因使用了十进制整数的方式进行编码，设计使用两个十进制数表示一个抗体，参数取值组合的索引则由码位的值来表示。

2.3亲和度函数

优化中抗体选择与否与该抗体值构造的支撑矢量机的分类效果有关。为了尽量降低计算的复杂度，笔者设计的亲和度函数如式(9)：

f=1/(1+F)

(9)

式中：F为漏报率。

3仿真结果

3.1实验中使用的数据集

为评价文中算法的性能，笔者选用汽轮发电机组的故障数据集作为实验数据，以机组常见的3种故障(油膜振荡F1，不平衡F2，不对中F3)为分析对象。表1列出了用于训练的代表性样本，数据中有振幅数据6个，f为发电机转子的频率。

表1汽轮发电机组数据集Table 1Turbo generator data set

3.2获得优化后的参数

选择好实验用的数据集后，利用免疫克隆选择算法根据分类器在分类过程的漏报率进行优化获得优化的参数值。优化过程中当进行800次迭代时，亲和度的变化趋于稳定，最后得到优化后的结果为：C=6.4，ξ=3.9，σ=0.026；为了避免优化过程中的偶然性，提高参数的可靠性，所给出的优化参数是30次试验的均值。

3.3实验结果及分析

在此使用两个指标对算法的性能进行评价，一个是能够正确检测的比率(既检测率)，记作TDR(true detection rate)；另一个是错误检测的比率(既误检率)，记作FDR(falsedetection rate)。在实验中还分别测试了标准SVM算法的诊断结果，实验结果如表2。

由表2看出：文中算法在检测率方面明显优于传统的SVM算法。在误检率方面也比传统的SVM算法低。

表2文中算法和标准SVM的性能比较Table 2Performance comparison of the proposed algorithm and the standard SVM

此外，笔者对引入优化算法后的算法执行效率情况进行了分析。图1表示在不同数据规模的情况下，使用文中算法和标准的支撑矢量算法进行分类器训练学习所消耗时间的比较。

图1文中算法和标准SVM训练时间比较Fig.1Comparison of the training time of the proposed algorithm and the standard SVM

由图1看出：由于笔者在参数优化时所选择的交叉验证的数据量比较小，使得文中算法和传统支撑矢量机的训练速度基本相当。从而也体现了文中算法在提高故障分类诊断检测正确率的情况下，并没有产生时间显著增加的问题，而在算法的诊断检测阶段，由于已经获得了优化的参数，因此在诊断阶段无需再附加优化的过程。

4结语

笔者研究了基于参数优化的支撑矢量机，引入免疫克隆选择算法采用交叉验证的方法，优化获得了支撑矢量机的参数，并在汽轮发电机组故障数据集进行了验证，从实验结果可以看出，文中方法在保证训练速度的基础上提升了识别正确率。

[1] SIMANI S，FANTUZZI C.Fault diagnosis in power plant using neural networks[J].InformationSciencesanInternationalJournal，2000，127(3/4)：125-136.

[2] MURALIDHARAN V，SUGUMARAN V，INDIRA V.Fault diagnosis of mono-block centrifugal pump using SVM[J].EngineeringScienceandTechnologyanInternationalJournal，2014，17(3)：152-157.

[3] 陆百川，张凯，马庆禄，等.基于数据驱动的数据故障诊断模型[J].重庆交通大学学报(自然科学版)，2014，33(5)：111-115.

LU Baichuan，ZHANG Kai，MA Qinglu，et al.Data fault diagnosis model based on data-driven[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2014，33(5)：111-115.

[4] JAYASWAL P，VERMA S N，WADHWANI A K.Application of ANN，fuzzy logic and wavelet transform in machine fault diagnosis using vibration signal analysis[J].JournalofQualityinMaintenanceEngineering，2010，16(2)： 190-213.

[5] 高振兴，郭创新，俞斌，等.基于多源信息融合的电网故障诊断方法研究[J].电力系统保护与控制，2011，39(6)：17-23.

GAO Zhenxing，GUO Chuangxin，YU Bin，et al.Study of a fault diagnosis approach for power grid with information fusion based on multi-data resources[J].PowerSystemProtectionandControl，2011，39(6)：17-23.

[6] 陆百川，郭桂林，肖汶谦，等.基于多尺度主元分析法的动态交通数据故障诊断与修复[J].重庆交通大学学报(自然科学版)，2016，35(1)：134-137.

LU Baichuan，GUO Guilin，XIAO Wenqian，et al.Fault diagnosing and modifying of dynamic traffic data based on MSPCA[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2016，35(1)：134-137.

[7] 王波，刘树林，张宏利，等.相关向量机及其在机械故障诊断中的应用研究进展[J].振动与冲击，2015，34(5)：145-153.

WANG Bo，LIU Shulin，ZHANG Hongli，et al.Advances about relevance vector machine and its applications in machine fault diagnosis[J].JournalofVibrationandShock，2015，34(5)：145-153.

[8] DU Haifeng，JIAO Licheng，WANG Sunan.Clonal operator and antibody clone algorithms[C]//InternationalConferenceonMachineLearningandCybernetics2002 Proceedings.IEEE，2002： 506-510.

[9] VAPNIK V N.TheNatureofStatisticalLearningTheory[M].New York： Springer-Verlag，1995.

(责任编辑：刘韬)

Support Vector Machine Based on Parameter Optimization and Its Application in Fault Diagnosis

CHEN Hu

(Chongqing Rail Transit (Group)Co.Ltd.，Chongqing400042，P.R.China)

In order to effectively diagnose the fault of the equipment，a support vector machine algorithm based on parameter optimization was proposed.Firstly，the immune clonal selection mechanism was introduced.The antibody group was constructed，in which an antibody was expressed in two decimal numbers.Then，the affinity function was established on the basis of the missing report rate.Thus，the parameters of support vector machine were optimized.After that，the support vector classifier with optimized parameters was constructed and used to classify and detect the equipment data.Simulation verification was carried out on the data of turbo generator set.The simulation results indicate that the proposed algorithm does not significantly increase the training time，compared with the traditional support vector machine algorithm.Moreover，it can effectively improve the detection rate and reduce the false detection rate.

electromechanical engineering; fault diagnostics; support vector machines; parameter optimization; immune clone algorithm

TH17

A

1674-0696(2017)10-119-04

2016-03-16；

2016-06-16

国家安全监管总局科技攻关项目(zhishu-031-2013AQ)

陈虎(1982—)，男，山东冠县人，工程师，主要从事事故诊断与检测方面的研究。E-mail： chenhu531@163.com。

10.3969/j.issn.1674-0696.2017.10.20