基于初始孔压非均布条件的软黏土地基固结特性分析

李之达，邵玉

(武汉理工大学 交通学院，湖北 武汉 430063)

基于初始孔压非均布条件的软黏土地基固结特性分析

李之达，邵玉

(武汉理工大学 交通学院，湖北 武汉 430063)

将初始孔压非均布条件用统一表达式表示，采用Merchant模型推导了初始孔压非均布条件下的竖井地基黏弹性解。通过与初始孔压均匀分布条件下的黏弹性解对比，验证了本文解的正确性。并编制计算程序分别分析黏弹性参数、初始孔压参数对于竖井地基固结特性的影响。研究表明：k及η值的增大均使固结速率降低，使同等深度的平均孔压增大，且对竖井地基平均孔压的影响较其对平均固结度的影响明显；同样条件下，k值的变化对竖井地基固结特性的影响更大。

岩土工程；非均布初始孔压；黏弹性；固结特性

0引言

为缓解土地压力，围海造地已成为广泛推广的有效方法之一，其中真空预压法与堆载预压法也得到了广泛应用，进而带动竖向排水地基理论的发展。近年来，现场试验与室外试验均表明，由于井阻作用的存在[1]，使得真空加载所产生的负压及堆载施加所产生的附加应力随着竖井的深度递减。B.INDRARATNA等[2]引入负压线性衰减模式，得到径向渗流情况下的竖井地基解析解；周琦等[1]引入时间衰减系数得到了相应的解析解；徐妍等[3]针对初始孔压非均布的情况，将初始孔压分为3种形式进行了线弹性固结理论的推导；近年来学者们结合涂抹区渗透系数[4]、复合地基[5]、竖井地基起始比降[6]和双层地基[7]进行了研究。因此考虑初始孔压具有实际意义与理论意义。

而就竖向排水地基而言，考虑土力流变模型更贴近工程实际。多年来已有大量学者基于Merchant模型对竖井地基黏弹性理论进行了深入研究：刘兴旺等[8]分别考虑自由应变和等应变，给出了竖井地基固结特性黏弹性解；王瑞春等[9-10]就半透水边界和变荷载条件进行了推导；刘加才等[11-12]分别针对均质深厚软土地基竖井未打穿情况，就层状黏弹性地基得到了相应的解答。

但是在黏弹性理论中，尚未考虑初始孔压非均匀分布的情况。有鉴于此，笔者将其采用统一表达形式表示，基于Merchant模型给出了初始孔压非均布条件下的解析解，并在此基础上进行程序编制分析黏弹性参数及初始孔压参数对地基固结的影响。

1计算简图

图1为笔者所用计算简图。竖井地基为打穿，边界条件为单面排水。不考虑侧向变形。图1中：l为竖井计算长度，等于其软土层厚度；Kh、Kv分别为竖井水平向和竖向渗透系数；Ks、Kw分别为涂抹区和竖井区渗透系数；rw、rs、re分别为竖井区、涂抹区和竖井影响区的半径。

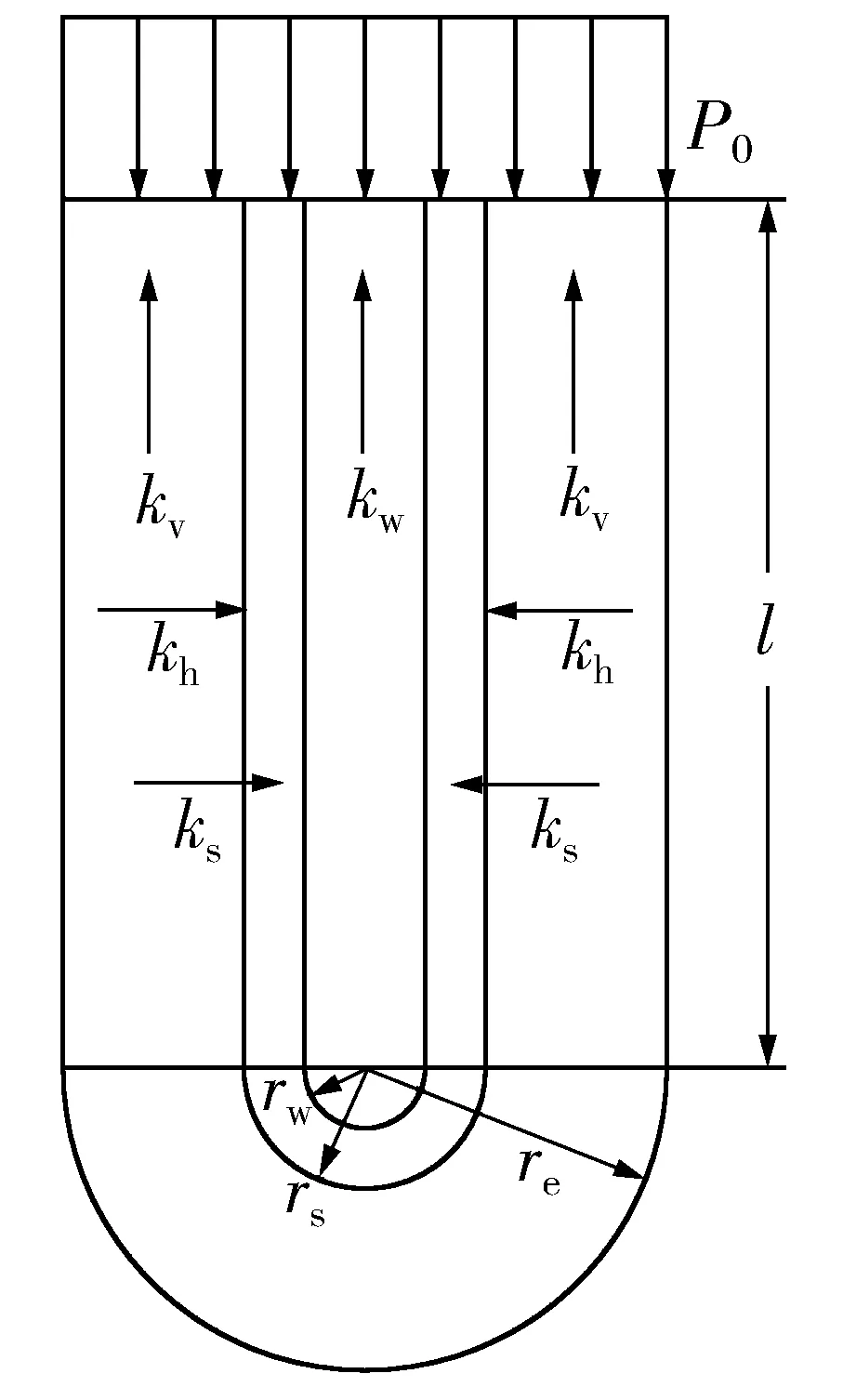
图1竖井地基计算简图Fig.1Calculation sketch of soil ground with vertical drain well

图2为Merchant流变模型示意，假定应力不变的条件，应变随时间的关系式为

(1)

式中：E0、E1分别是两弹簧的模量；K1是黏壶的黏滞系数。

图2Merchant模型Fig.2Merchant model

其柔度函数为

(2)

式中：η=E1/K1。

主要假设与文献[11]相同。

2控制方程

控制方程如下：

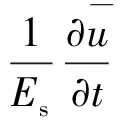
(3)

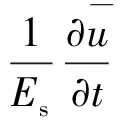
(4)

(5)

(6)

3求解条件

1) 连续条件：

usr=rw=uw；

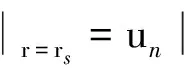
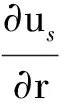
2) 边界条件：

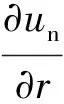
3) 初始条件：

u0(z)为沿深度分布的初始孔压：

其中当k=0时，初始孔压分布为倒三角形分布；当k变动时呈梯形分布；当k=1时，初始孔压分布为矩形分布。具体见图3。

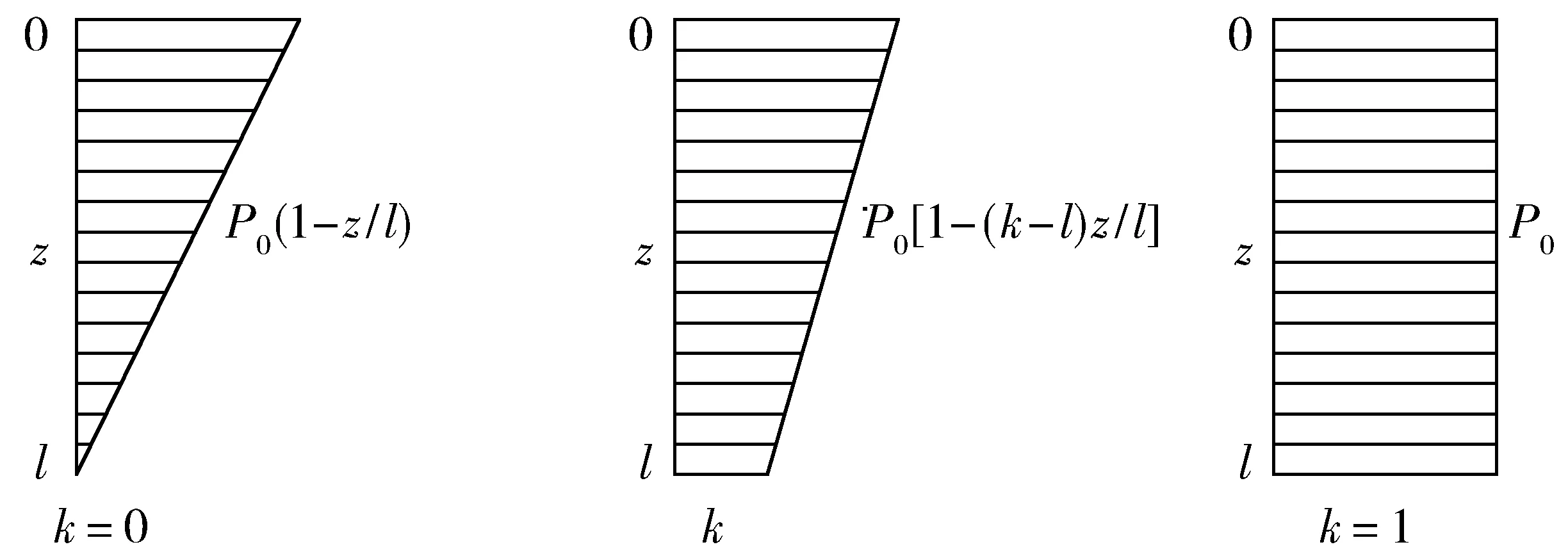
图3孔压分布Fig.3Distribution of initial pore pressure

4方程的求解

根据文献[8]的推导思路，设：

uw(z，t)=Zw(z)T(t)

可得：

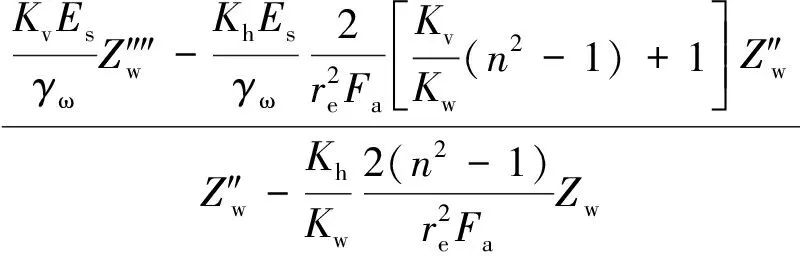
(7)

可得两个微分方程：

(8)

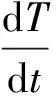
(9)

先求解方程(8)的解为

(10)

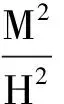
(11)

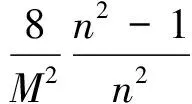
再求解方程(9)，得

Twm(t)=AwmTm(t)=

(12)

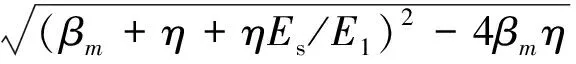
则：

(13)

(14)

(15)

而u0(z)=p0[1+(k-1)z/l]，则根据三角函数的正交关系可得：

(16)

所以：

(17)

(18)

按孔压定义的固结度为

(19)

(20)

当k=0(即初始孔压呈三角形分布)时

(21)

(22)

当k=1(即初始孔压呈矩形分布)时：

(23)

(24)

令η=0时所得结果与文献[3]结果一致，可证明其正确性。

5固结特性分析

重点为分析黏弹性参数η和初始孔压参数k对固结特性的影响，因此取某高速公路试验段参数进行分析。竖井打设长度为20 m，软土层以下视为不透水层。采用排水固压预压法。其计算参数为

l=20 m，re=0.35 m，rs=0.07 m，rw=0.035 m，n=re/rw=10，s=rs/rw=2，Kh=2.0×10-8m/s，Kw=2.0×10-4m/s，Ks=1.0×10-8m/s。

软土的力学指标为

Es=1.5 MPa，Ch=2Cv=3×10-7m2/s，E1=3 MPa。

为便于工程应用，将以上解答编制成为相应的计算程序，并结合实例进行分析。

图4、图5反映了k=1(初始孔压为矩形分布)时，η变化时平均孔压及竖井打设区平均固结度的变化情况。从图4、图5可以看到：取Th=200时竖井打设区η=0(线弹性解)的平均固结度与黏弹性解相差约为4%。黏弹性参数η由小变大时，即K1由大变小时，黏弹性土体前期固结速率较快，后期固结速率反而降低，而平均孔压在相同时间的条件下随之增大。

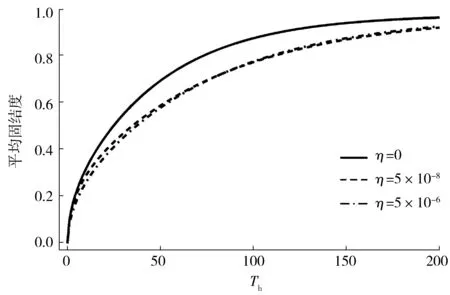
图4不同η时平均固结度比较Fig.4Comparison of average consolidation degrees with different η

图5不同η时平均孔压比较(Th=10)Fig.5Comparison of average EPP with different η(Th=10)

图6不同k时平均固结度比较Fig.6Comparison of average consolidation degrees with different k

图6、图7反映了当η=5×10-8/s时，k=0，0.5，1.0时竖井区内的平均孔压及平均固结度的变化情况。

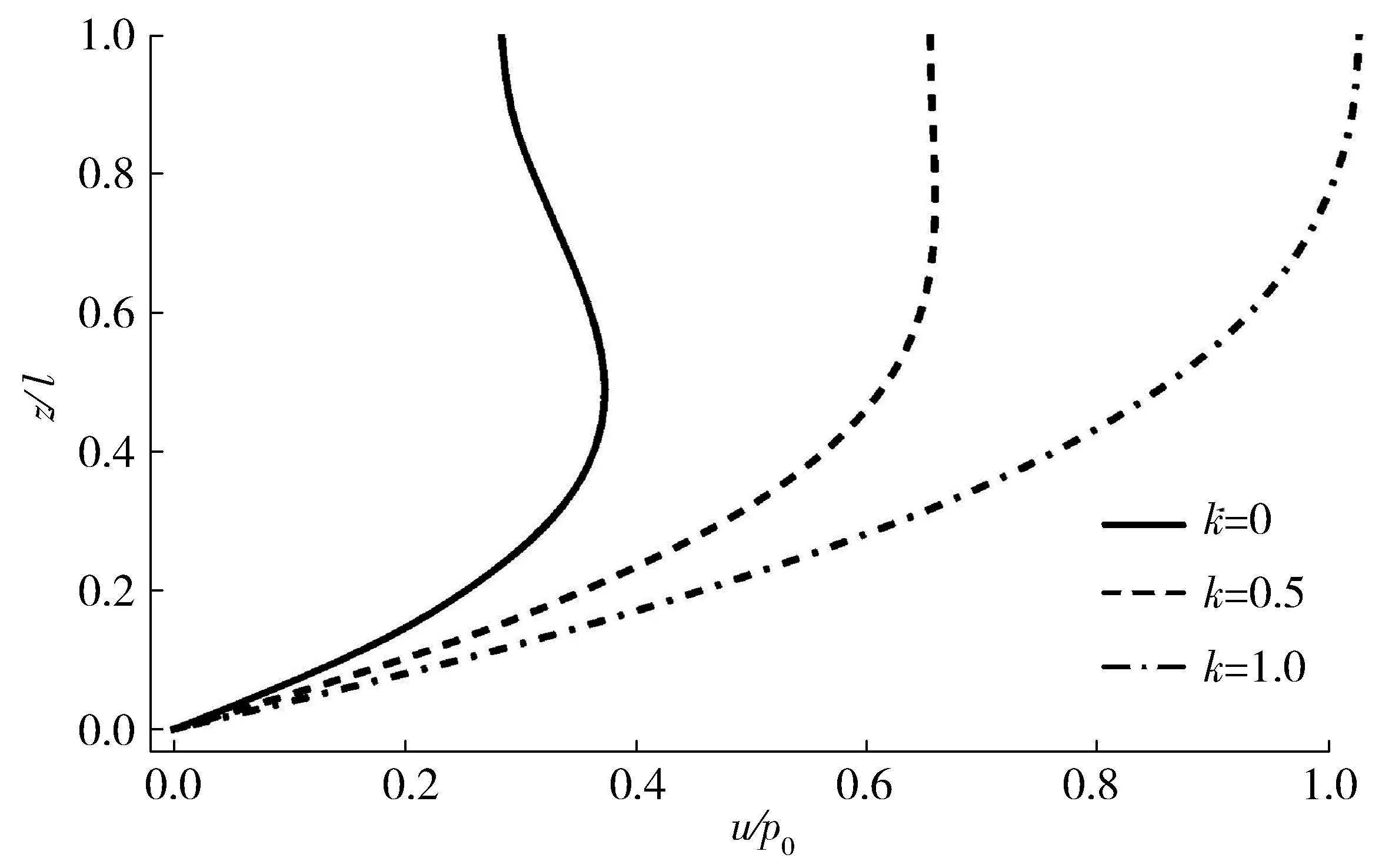
图7不同k时平均孔压比较(Th=10)Fig.7Comparison of average EPP with different k(Th=10)

从图6、图7可以看到：取Th=200时竖井打设区k=0，0.5，1.0时的平均固结度分别为95.79%、94.73%和94.21%。随着k值增大，平均固结度及平均孔压曲线右移，其固结速率减慢，相同深度下平均孔压增大。说明在初始孔压均布由倒三角形向矩形分布变动的过程中，三角形的分布形式最利于固结度的完成，但是对于平均孔压来说，最有利形式为矩形分布形式。

图8不同k，η时平均固结度比较Fig.8Comparison of average consolidation degrees with different k，η

图8、图9反映了不同k，η取值下平均孔压及平均固结度的变化情况。从图8中可以看到，当k=0，1.0时，η的增大对于土体固结度的影响分别为0.38%、0.54%，且随着η的增大，前期土体固结速率较慢，后期较快；当η=5×10-8，5×10-6时，k的增大对于土体固结度的影响分别为1.65%、1.5%，且随着k的增大，固结曲线右移，固结速率减慢。从图9中可以看到，k极大的影响平均孔压的变化形式，而η只在一定程度影响其变化速率。综合而言，k值的变化对竖井地基固结特性的影响更大。

图9不同k，η时平均孔压比较(Th=10)Fig.9Comparison of average EPP with different k，η(Th=10)

6结论

1) 采用基础的Merchant流变模型，从现有的初始孔压非均布线弹性解答出发，得到了相应的竖井地基黏弹性解答，并分析了初始孔压参数及黏弹性参数。

2) 黏弹性参数η的增大，对基于孔压的固结度的影响是负面的，对平均孔压的影响是正面的。

3) 在初始孔压非均布的黏弹性解答中，k值的变化对竖井地基平均固结度及平均孔压均产生影响且对后者影响较明显。初始孔压均布由倒三角形向矩形分布变动的过程中，三角形的分布形式最利于固结度的完成，但是对于平均孔压来说，最有利形式为矩形。

4)k值会极大的影响地基固结特性的变化形式，而η只在一定程度影响其变化速率。相较而言，k值的变化对竖井地基固结特性的影响更大。

[1] 周琦，张功新，王友元，等.真空预压条件下的砂井地基Hansbo固结解[J].岩石力学与工程学报，2010，29(增刊2)：3994-3999.

ZHOU Qi，ZHANG Gongxin，WANG Youyuan，et al.Hansbo’s consolidation solution for sand-drained ground under vacuum preloading[J].ChineseJournalofRockMechanicsandEngineering，2010，29(Sup2)： 3994-3999.

[2] INDRARATNA B，RUJIKIATKAMIORN C，SATHANANTHAN L.Analytical and numerical solutions for a single vertical drain including the effects of vacuum preloading[J].CanadianGeotechnicalJournal，2005，42(4)： 994-1014.

[3] 徐妍，吴芳，谢康和，等.初始孔压非均布竖向排水井地基固结方程的解析解[J].水利学报，2008，39(7)：829-835.

XU Yan，WU Fang，XIE Kanghe, et al. Analytic solution of consolidation equation for soft soil with vertical drains subject to non-uniformly distributed initial pore water pressure[J].JournalofHydraulicEngineering，2008，39(7)： 829-835.

[4] 蔡新，谢康和，徐妍，等.初始孔压非均布条件下涂抹区渗透系数变化的砂井地基固结解[J].岩土工程学报，2010，32(1)：104-108.

CAI Xin，XIE Kanghe，XU Yan，et al.Analytical solution for consolidation of sand-drained ground under non-uniform distribution of initial excess pore water pressure and variation of permeability coefficient in smear zone[J].ChineseJournalofGeotechnicalEngineering，2010，32(1)：104-108.

[5] 张玉国，岳峰，谢康和.初始孔压非均布条件下散体材料桩复合地基固结理论研究[J].岩土力学，2011，32(9)：2675-2680.

ZHANG Yuguo，YUE Feng，XIE Kanghe.Study of consolidation theory of composite ground with granular columns under non-uniform distribution of initial excess pore water pressure[J].RockandSoilMechanics，2011，32(9)：2675-2680.

[6] 王坤，谢康和，刘兴旺，等.初始孔压非均布考虑起始比降的一维固结解[J].岩石工程学报，2011，33(9)：1419-1424.

WANG Kun，XIE Kanghe，LIU Xingwang，et al.Solution for one-dimensional consolidation with threshold gradient subjected to non-uniformly distributed initial pore water pressure[J].ChineseJournalofGeotechnicalEngineering，2011，33(9)：1419-1424.

[7] 江唯伟，张军辉.初始孔压非均布双层地基一维固结性状分析[J].长江科学院院报，2013，30(9)：80-84.

JIANG Weiwei，ZHANG Junhui.One dimensional consolidation behavior of double-layered ground with non-uniform distribution of initial pore water pressure[J].JournalofYangtzeRiverScientificResearchInstitute，2013，30(9)： 80-84.

[8] 刘兴旺，谢康和，潘秋元，等.竖向排水井地基粘弹性固结解析理论[J].土木工程学报，1998，31(1)：10-19.

LIU Xingwang，XIE Kanghe，PAN Qiuyuan，et al.Viscoelastic consolidation theories of soils with vertical drain wells[J].ChinaCivilEngineeringJournal， 1998，31(1)： 10-19.

[9] 王瑞春，谢康和.半透水边界的竖向排水井地基粘弹性固结分析[J].长江科学院院报，2001，18(6)：33-36.

WANG Ruichun，XIE Kanghe.Analysis on viscoelastic consolidation of soil foundations by vertical drain wells considering semi-permeable boundary[J].JournalofYangtzeRiverScientificResearchInstitute，2001，18(6)： 33-36.

[10] 王瑞春，谢康和.变荷载下竖向排水井地基粘弹性固结沉降解析解[J].土木工程学报，2001，34(6)：93-99.

WANG Ruichun，XIE Kanghe.Analytical solutions for viscoelastic consolidation by vertical drains under time-dependent loading[J].ChinaCivilEngineeringJournal，2001，34(6)： 93-99.

[11] 刘加才，赵维炳，明经平，等.均质未贯穿竖井地基粘弹性固结分析[J].岩石力学与工程学报，2005，24(11)：1972-1977.

LIU Jiacai，ZHAO Weibing，MING Jingping，et al.Viscoelastic consolidation analysis of homogeneous ground with partially penetrated vertical drains[J].ChineseJournalofRockMechanicsandEngineering，2005，24(11)：1972-1977.

[12] 刘加才，马强.层状粘弹性地基一维固结特性[J].土木建筑与环境工程，2012，34(3)：34-38.

LIU Jiacai，MA Qiang.One dimensional consolidation analysis of layered clay soils exhibiting rheological characteristics[J].JournalofCivil，ArchitecturalandEnvironmentalEngineering，2012，34(3)： 34-38.

(责任编辑：谭绪凯)

Consolidation Characteristics of Soft Clay Ground Subject to Non-uniformly Distributed Initial Pore Pressure

LI Zhida，SHAO Yu

(School of Transportation，Wuhan University of Technology，Wuhan 430063，Hubei，P. R. China)

A new solution under the non-uniform distribution of initial pore pressure expressed in a unified expression was derived from the equivalent strain governing equation for the consolidation by vertical drain wells on the basis of the Merchant rheological model.The correctness of the proposed solution was verified by comparing with the viscoelastic solution under the uniform distribution of initial pore pressure.The calculation program was coded to analyze the influence of the viscoelastic parameters and the initial pore pressure parameters (described bykandη)on the consolidation characteristics of soil ground with vertical drain wells.The research shows that the increase ofkandηwill slow down the rate of the consolidation，and increase the average pore pressure at the same depth.The increase ofkandηhas more significant influence on the average pore pressure of soil ground with vertical drain wells than that on the average degree of consolidation; under the same condition，the change ofkmakes much more influence on the average degree of consolidation than that on the average pore pressure of soil ground with vertical drain wells.

geotechnical engineering; non-uniformly distributed initial pore pressure; viscoelastic characteristics; consolidation characteristics

U416.1；TV223.2

A

1674-0696(2017)10-045-06

2016-08-20；

2017-02-13

李之达(1957—)，男，湖南平江人，教授，博士生导师，主要从事工程材料流变、破坏与损伤方面的研究。E-mail： zhidali@163.com。

10.3969/j.issn.1674-0696.2017.10.08