研究性公开课的实践和思考
沈 军
江苏省扬州中学 (225009) 戚有建江苏省高邮中学 (225600)
研究性公开课的实践和思考
沈 军
江苏省扬州中学 (225009) 戚有建江苏省高邮中学 (225600)
随着高中数学新课改的推进,“研究性学习”的观念越来越得到大家的认可,作为一线教师,笔者也在努力创造研究性学习的实践机会.笔者发现,在课堂教学中进行研究性学习,既能提高课堂效率,提高学生的学习成绩,又能逐步改变学生的学习方式,提高学生的学习兴趣,提高学生的创新精神和实践能力.前不久,应江苏省滨海中学所邀,笔者去滨海中学上了一节研究性公开课,下面是本人这次公开课的教学过程和教学感想.
一、问题引入

图1
问题如图1,在ΔABC中,AB=2x,AC=x,BC=6,求ΔABC面积的最大值.
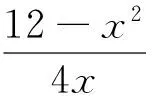
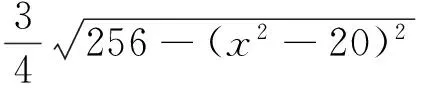
点评:解法1是处理最值问题的通法,即构建目标函数求最值,多数学生能想到这种解法,教学中可探讨:求哪个角的余弦值好?很多学生求的是cosA,实际上求cosC更好,因为cosC的表达式更简单些,另外,教学中,有少部分学生打算作高(例如AD)然后用勾股定理求高从而求三角形面积,这种想法也可以,但是要按照D点在线段BC上还是在线段BC的延长线上讨论处理.

图2
解法2(借助A点轨迹求最值) 如图2,以BC所在直线为x轴,BC的中点为坐标原点,建立坐标系,则B(-3,0),C(3,0),设A(x,y),由AB=2AC,得(x-5)2+y2=16,所以A点的轨迹为圆(去掉与x轴的交点),不难发现,当A(5,±4)时,三角形的高最大,对应的面积最大,所以ΔABC面积的最大值为12.
点评:解法2实际上是用方程来研究曲线,即用坐标法来研究动点A的轨迹,只要将几何关系AB=2AC坐标化即得圆的方程(x-5)2+y2=16,“圆”来如此,直观形象,充分体现了解析法的基本思想,下面很容易发现三角形高的最大值就是圆的半径,从而很容易求得三角形面积的最大值.通过解法2很自然就能引出这节课的主题——阿波罗尼斯圆.
二、知识构建
1.阿氏圆定义

图3


2.命题结构

三、变式研究
变式1 在ΔABC中,AB=AC,D是AC中点,

分析:先考虑ΔABD面积的最大值,因为AB=2AD,所以A点的轨迹为阿氏圆.
(答案:24.)
点评:变式1中用向量形式来呈现长度,需要学生能挖掘出题目中隐含的阿氏圆并用来解决问题.另外,从变式1出发,也可以让学生自己进行变式编制习题(要尽量将变式的权利交给学生,让学生自己去变,在变中体会不变),教学中,很多学生编制了下面的变式2.

分析:先考虑ΔABD面积的最大值,因为AB=3AD,所以A点的轨迹为阿氏圆.

点评:教学过程中,可以探讨:能否不求出阿氏圆的方程就能知道阿氏圆的半径?实际上是可以的,因为在上面图3中, 直径MN的两个端点M,N实际上是AB的两个内外分点.




变式4 已知A(0,3),B(0,0),圆C:(x-a)2+(y-2a+4)2=1上存在点P满足PA=2PB,求a的取值范围.
分析:在ΔPAB中,因为PA=2PB,所以P点的轨迹为阿氏圆,又因为P点在圆C上,所以问题转化为阿氏圆和圆C有交点.

点评:本题是14年江苏高考题,江苏高考最近几年多次考到阿氏圆,08年考到,14年又考到,命题专家为何对阿氏圆情有独钟呢?实际上通过阿氏圆是为了考查解析法的基本思想,即用方程来研究曲线.
四、逆向研究

如果交换条件和结论,就可以研究下列两类问题:①③⟹②;②③⟹①.




答案:存在A(-2,0),B(4,0)或A(-6,0),B(-12,0)满足要求.



答案:B(4,0).
点评:教学中,可以探讨能否先猜出定点B的坐标,实际上是可以的,先借助对称性可以确定定点B在x轴上,再特殊化处理,例如取P点为(0,0),
(-8,0),从而求出点B的坐标为(4,0),下面只要验证B(4,0)符合要求,此时实际上也就是上面的变式5.
五、类比研究
阿氏圆与“距离之比为定值”有关,类似的我们可以联想到“距离之和为定值”,“距离之差为定值”,或者“距离之积为定值”,所以就可以研究下面的问题.
变式8 在ΔABC中,AB=6-x,AC=2,BC=x,求ΔABC面积的最大值.
分析:在ΔABC中,因为BA+BC=6>2,所以B点的轨迹为椭圆(去掉左右顶点).

变式9 在ΔABC中,AB=6+x,AC=10,BC=x,则ΔABC面积存在最大值吗?
分析:在ΔABC中,因为BA-BC=6<10,所以B点的轨迹为双曲线的一支(去掉顶点)
答案:无最大值.
点评:“距离之积为定值”的问题难度稍大,它与卡西尼卵形线有关,可以留给学生课后去研究.
一节课很快就结束了,这节课学生一直都沉浸在发现问题、提出问题、分析和解决问题的喜悦中,看到学生精彩的表现,看到学生满意的眼神,回馈我的是欣喜、是思考.
六、教学反思
1.研究性课堂是实践新课程理念的有效途径
教学方式的转变是新课程改革的本质要求,新课程强调,教师要更新教育观念,改变教学方式,让学生由被动学习转变为主动学习,倡导通过各种不同形式的探究活动,让学生亲身体验数学发现和创造的过程,培养和提高学生的创新能力.本节课中,教师由原来的知识传授者转变为学生学习的组织者、引导者、合作者与共同探究者,学生从原来的被动接受者转变为主动探究者,体验到了数学的乐趣、体验到了探究的乐趣、体验到了成功的乐趣.
2.研究性课堂可以从问题开始
问题是思维的动力,一个有价值的问题是研究性课堂成功的前提.这个问题要具有以下特征:①问题要有一定的知识容量,涉及到的知识面要宽、思想方法要多;②问题要具有层次性,可供不同水平学生作不同层次的探究;③问题要具有开放性,探究的过程和结果丰富多彩;④问题要具有沿展性,可供学生发现新问题作进一步的探究.波利亚也说过“一个好的教师能够拿出一个有意义的题目,去帮助学生发掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域”.
3.研究性课堂中要放手让学生去自主探究、去体验(成功和失败)


