解题教学：重在通过解题活动深化学生数学思维*

潘小明

江苏省泰州学院 (225300)

解题教学：重在通过解题活动深化学生数学思维*

潘小明

江苏省泰州学院 (225300)

数学教学是数学活动的教学，作为数学教学重要环节和重要内容的解题教学自然也是解题活动的教学.解题教学既然是解题活动的教学，就应当是一个有着思路探究和结果整理的思维过程.由此，在解题教学过程中应当重视师生双方解题过程的暴露.对在解题教学中起主导作用的教师而言，尤其要注意合理暴露诸如“思路寻探”“方法优化”“结果分析”“监控调节”和“过程反思”等关键性解题思维过程.缺少对解题活动过程的有效暴露，解题教学很容易沦为机械性的刺激反应活动，学生不仅难能经由解题实践激发有深度的数学思维，而且难能经由“问题理解”“思路寻找”和“获得解答”这一系列的过程学会如何解题.相反，不良的解题习惯还会使越来越多的学生在对“解题方法模仿”“解题结论记忆”的过程中走向不是深度而是表层化的数学学习.本文拟结合一则数学教学案例的分析，讨论当下的数学解题教学何以会异化数学解题的活动？何以会分裂解题活动与数学思维的对接？并在此基础上初步探讨如何改进数学解题教学的对策.

一、教学案例的描述

Y老师在高二(3)班给学生提供了如下一道数学题：已知函数f(x)=ax2+bx,且1≤f(-1)≤2,2≤f(1)≤4,试探求f(-2)的取值范围.

Y老师认为，这道题并不是太难，自己所教的班级是重点班，他想，“学生会的自己就不必多费口舌”“今天要完成的教学工作量比较大，这道题交给学生自己来解决”.基于自己的思考，Y老师在出示题目后，要求学生自己来“做一做”，并让一位他认为解题能力不错的学生1到讲台前的黑板上进行板演.学生1的板演如下：

Y老师一看，答案与自己的完全相同，应当没有什么漏洞，于是笑着说：“大家看一看，这个解法是正确的.如果没有什么问题，我们就来做下面的一道题.”

就在老师准备就此而过的时候，学生2突然举手要求发言.“嗯，有人举手了.好的，你有什么问题？请讲！”Y老师对学生2微笑说.

解:∵f(-1)=a-b,f(1)=a+b,f(-2)=4a-2b,由已知条件有1≤a-b≤2,①2≤a+b≤4,②∴3≤2a≤6.又∵4a-2b=2a+2(a-b),∴3+2×1≤f(-2)≤6+2×2.即所求f(-2)的取值范围为[5,10].

学生2：老师，我的答案和黑板上的不一样！

Y老师：你是不是哪儿不小心，算错了？你得认真仔细地重新检查一下！

学生2：老师，我认真检查过了，我的答案没问题！

师：怎么可能？你肯定在某个地方搞错了.好吧，你也到前面来，在黑板上把你的解题过程写出来，让大家帮你看看问题究竟出在哪儿？

学生2根据教师的指令在黑板上写下了自己的解题过程.

解:∵f(x)=ax2+bx,1≤f(-1)≤2,2≤f(1)≤4,∴1≤a-b≤2,①2≤a+b≤4,②①+②得3≤2a≤6,即32≤a≤3,③由②得-4≤-(a+b)≤-2,④①+④得-3≤-2b≤0,即0≤b≤32⑤③×⑤+⑤×(-2)得3≤4a-2b≤12,∴所求f(-2)的取值范围为[3,12].

Y老师一看，答案确实不一样!学生1的解答与自己的解答、参考书上的解答都是一样的.学生2的解答肯定是错了，那么，错在哪儿呢？Y老师用眼睛再一次瞄了瞄黑板，一下子没有看出学生2的解法致错的原因.怎么办？Y老师头脑迅速地转着，他决定将解题的皮球先踢给下面的学生们.

Y老师：同学们一起来看看，现在有了两种不同的解答了，结果不同.那么谁对谁对？错在什么地方呢？大家可以相互讨论.

老师的话音一落，教室里叽叽喳喳地议论了起来，“第二种解答肯定是错的！”“我的解答和第一种相同，可第二种答案看来也不错呀！”“第一个结果是第二个结果的真子集”“第二个范围更大”“也许这两种解答都不对”……教室里看来有点乱.

利用学生相互讨论的这段时间，Y老师自己对解答有了正确的判断：学生2的答案是错误的，他问了几个学生对学生2解答的看法，见学生说不出一个所以然，他想，“如果再问下去，肯定是浪费时间，自己还有任务要完成”“干脆自己来讲吧！”于是他果断地把自己对学生2解法的正确认识当众揭晓.

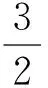
Y老师讲解后，再也没有其他学生提出异议.Y老师终于舒出了一口气，接着讲解他预先备好的下一道题……

二、教学案例的反思

这个案例可以从多个角度来反思，从“解题活动”“数学思维”两个角度来反思，我们可以提出如下的一些问题：Y老师是如何展开解题教学的？在这一解题教学中，存在着哪些解题活动？主导教师解题活动的内在因素是什么？Y老师的解题价值观可能是什么？从学生的表现看，Y老师解题教学能否算成功？为什么？在这一解题教学中，学生在思维训练方面有哪些收获？存在哪些不足？为了进一步深化学生的数学思维，类似的解题教学还可做哪些改进？下面就尝试所提出的问题作一些分析.

Y老师主要是通过“让学生做题”“让学生板演”“让学生提问”“自己讲解”来展开教学的，之所以这样展开教学，是因为Y老师有着诸如“这道题并不是太难”“所教的班级是重点班”“学生会的自己就不必多费口舌”“今天要完成的教学工作量比较大，这道题交给学生自己来解决”等一系列的教学预设.表面看来，Y老师的教学预设中也有着浓浓的“学生主体意识”“课堂效率意识”.所谓的“学生主体意识”，在这里主要表现为数学教学要让学生动脑、动手，先有学生的做数学，再有教师的讲数学.而所谓的“课堂效率意识”，在这里主要表现为“学生会的教师就不讲”“教师课堂语言精练”，尽可能节约时间、尽可能多讲解一些题目.然而从实际效果来说，教师并没有真正体现“学生主体意识”，比如，对学生2解法的分析最终仍是教师“塞给学生的”“是直接向学生奉送答案的”.Y老师没有真正地认识到，自己所教的班级有着近50名的学生，他们有着不同的数学基础、思维风格，他们不是空着脑袋走进教室的，他们不应象一张白纸一样任由教师涂画，也不应象一个空洞的容器一样任由教师直接塞正确的解法.教学认识的缺失必然导致教学行为的不当，由Y教师主导的解题教学中就实然地丧失或减弱了学生的主体性.事实上，尽管有许多学生在解法上与学生1的解法相同，但是，他们为什么这样解？同一解法背后是否都有着同样的数学思维？教师没有探究，也不知晓.此外，在Y老师讲解学生2解法错误的原因之前，他也听到了教室里一些叽叽喳喳的议论——“第二种解答肯定是错的！”“我的解答和第一种相同，可第二种答案看来也不错呀！”第一个结果是第二个结果的真子集”“第二个范围更大”“也许这两种解答都不对”，由于当时忙于思考如何评判学生2解答的科学性，所以，尽管Y老师听到了议论，而且这些议论中可能会有一些值得进一步挖掘的教学资源，但他并没有真正有效利用学生的议论，本质上就是无视学生的存在.其次，教师也没有真正体现“课堂效率意识”，简单地把一道题一带而过，教师内心贪图的是讲更多的题，本质上是长期存在的“题海战术”教学思想在作怪.数学问题似海洋，题海战术很荒唐，所以尽管人们强调数学学习要多做题，但不主张题海战术.比如，曾经用麻袋装草稿的数学家陈景润在与他的学生讨论数学解题时也强调“题有千变，贵在有根”，认为只有寻探到了题目的“根”，才能促进学生数学核心素养的提高.这也表明，做数学题目、教数学题目，贵在将题目做透，贵在将学生的数学思考通达至题目的“根子上”，只有这样，学生才能“举一反三”“触类旁通”，让做过的数学题目具有真正的“生长性”和教学效益.在解题教学中顾数量不顾质量显然不是真正意义上的“讲效率”，也不是“精讲精练”的内在要求.

从总体上说，Y老师对于这道题目的教学尽管有一些优点，但确实不能算成功.虽然我们可以看到，在这一解题教学过程中已经有学生“动了起来”——“做题”“板演”“交流”“讨论”，等等，但这些“动起来”并非是真正意义上的数学活动，因为这些“动起来”并未与思维暴露、思维内容、思维深化有机融合起来.学生1的解答虽然是正确的，但他是如何思考的？不得而知.学生2的解答虽然是错误的，但他错误的结果与学生1正确的结果又存在着一定的关系(学生2所求解集真包含学生1所求解集)，为什么会这样？学生在解题活动过程中出现错误是一种正常甚至是必然的现象，由此对于解题教学而言，教师就应当认识到对学生错解的分析与处理是解题教学重要、必要而又非常正常的业务，并且，由于来自学生的错解具有“正例示范所不可替代的作用”，所以合理处理学生的错解有利于发展学生的批判性思维和提高解题教学的完整性.特别地，应当看到，来自学生的错解或相关的疏忽，既可能产生一些消极的教学因素(如耗时、费口舌、学生丧失信心、影响士气)，也有可能产生一些积极的教学因素(如借机完善学生的数学认知结构、加强数学知识的联结).在本教学中，Y老师对此显然缺少正确的认识.从逻辑上讲，教学过程中出现了两种具有包含关系的结果可以证明至少有一种解答是错误的，利用学生讨论的时机，教师把学生2出错的原因想通了，并进行了讲解，但这样的教学并没有能正视学生“也许这两种解答都不对”的担心，源于数学知识的逻辑分析并不等于学生心理上的接受，更不等于学生有深度的数学思维和更本质的数学理解.这是因为，学生2的出错并不能保证学生1的正确，即使学生1的解答与参考答案以及老师本人的解法相同，也不能保证这种解法一定是正确的(尽管它确实是正确的).至少，仅仅用教师本人对一种错误分析的讲解还不能揭示数学题目真正的“数学化”本质，教师替代性数学思考远远不能等同于学生建构性数学思考.

从根本上说，Y老师在解题教学中并未将“解题活动”与“思维活动”有效对接.解题思路的探求主要反映解题者的思维活动过程，所求问题答案的呈现主要反映解题者数学思维活动的结果.Y老师在解题过程中更多关注了解题的结果，对解题思路的探求过程还没有高度重视，比如，除了如学生1的解题思路外，还有没有其他的解题思路？在不同的解题思路中，哪些或哪一个是更为本质的？不同的解题思路之间有着怎样的内在联系？诸如此类的问题，教学中都没有涉及.当然，Y老师自己本人也存在着“麻痹”“轻视”的心理，他因为自己在备课时很快做出了答案并且和参考答案相符，就没有对题目进行深究，这其实也反映了教师解题习惯和数学核心素养的不足，特别是当他看到学生2错误的解答后并未能迅速定位学生出错的原因和有效的教学，也进一步反映了数学功底和教学能力的欠缺.在现实的数学解题教学中，象Y老师这样的数学教师人数众多，他们喜欢将解题教学的关注点停留于最终解题结果的呈现，对于解题过程要么不敢暴露(教师自己事先看了参考答案然后照本宣科)，要么不会暴露，不能处理好暴露什么？如何暴露？暴露到什么程度？由于教师不会暴露解题思维，不少学生虽然能看得懂教师所提供的一些解法，但是相应的解法究竟怎么来的不得而知，长此以往，学生会感觉到从教师那里会有越来越多解题方法的简单堆积或者各种各样解题技巧的神秘出现.解题教学不仅要求教师懂数学、会做题，而且要求教师会暴露解题思维、揭示数学方法，只有合理暴露数学解题的过程和透彻地分析问题中所涉及数学知识和数学方法的本质，数学解题教学才能有较强的数学感染力和思维穿透力.忽视解题活动与数学思维的对接，教师讲题目觉得无聊，学生做题目觉得无奈，教和学的兴趣共同淹没在题海中，教和学的智慧共同丧失于傻练中.

三、改进教学的意见

就核心价值而言，解题教学要引导学生通过解题活动与数学思维的对接实现相关数学知识的掌握和数学能力的提高，为了实现这一核心理想，这道题的教学还可以从如下方面作一些优化或改进：

其一，教师本人要在事先立足于学生的深度学习进行充分的备课.深度学习更注重学习者的主动性、协作性和探究性，“三性”究竟如何通过教学设计来实现？数学问题背后隐藏着许多思想和方法，教师如何通过有效而深入分析予以揭示？提高解题教学的预见性关于在于对问题和学生的深研，为此，教师要深度预测学生在解题活动中可能性的解法及其可能性的错误，要自觉地防范和克服仅仅因教师个人解法与参考书“不谋而合”就不再深究的教学行为，要在平时加强自己的解题修养，要通过解题、读书(包括数学、教育和心理学等方面的书)、和他人交流和自主反思不断开阔自己的解题视野，要有意识地从数学教材、教参、教辅等现有资料的局限性中跳出来，除了将题目“做全”“做对”，还要将题目“做深”“做透”，要善于在更高的层次、更高的观点下看待自己的数学解题与教学实践，不断增强对数学题目和所教学生的理解.

其次，就学生解答，除了让学生板演“怎样解的”，还应当让学生说明“为什么这样解？是如何想到？”比如，对于学生1的正确解答，要防止“碰巧”产生的做法，而是要让学生说出对题目的理解，认识到其本质是已知a+b和a-b的范围，并据此求4a-2b的范围，在此基础上说明自己的解题思路的关键是“设法将4a-2b用a+b和a-b来表示”，本质上是一种从整体进行数学思考的方法.针对学生2的错解，教师自己明白了错因后，不能立即向学生讲解，而是引导学生对学生2的思维过程进行讨论，由于错误具有一定的隐蔽性，所以要舍得留时间给学生思考、讨论和交流，自己讲解后，要有恰当的机制评价学生“是否真的懂了”“是否真的掌握了”.

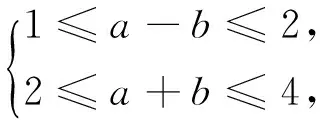
(1)若f(x)=ax2+bx，且1≤f(-1)≤2,2≤f(1)≤4，那么f(k)的范围是什么？(2)若f(x)=ax2+bx，且a1≤f(x1)≤b1,a2≤f(x2)≤b2,那么f(k)的范围是什么？(3)如果f(x)=ax2+bx+c，且1≤f(-1)≤2,2≤f(1)≤4,5≤f(2)≤10，能否求出f(3)的范围？

解题教学的重心不是解题，而是想法，如果教师仅仅引导学生根据已知条件和问题目标进行形式化的计算、推理、演绎，而不能涉及所求解问题背后的数学本质，即使做了很多题目，也无异于猪八戒吃了许多人参果食而不知其滋味，这样的解题教学就很难体现解题活动和数学思维的应有价值.为了提高解题教学的价值，教师在解题教学中应通过“解题活动”与“数学思维”自觉、主动的对接，巩固所学的数学知识与技能，增强对所学概念和命题的理解，优化数学思维的品质，将真正数学核心素养的培养落细、落实.

泰州学院教授博士基金项目“数学教师实践性知识研究”(TZXYJB/201502)阶段性成果之一.江苏省高校自然科学基金项目“关于拓扑空间中反射族的研究”(14KJB110024)阶段性成果之一.