基于QPSO的模糊分类系统优化设计*

诸云晖， 孙 俊

(江南大学 物联网工程学院，江苏 无锡 214122)

基于QPSO的模糊分类系统优化设计*

诸云晖， 孙 俊

(江南大学物联网工程学院，江苏无锡214122)

提出了构建模糊分类系统的有效方法。通过量子位选择的方法对初始的模糊规则进行优化，减少种群规模、提高全局搜索能力，且可以大幅缩短训练时间，达到快速收敛、有效分类的目的。为了优化模糊分类空间和减少模糊规则数目，提出了量子行为粒子群优化(QPSO)算法,提高初始模糊分类系统的性能。实验结果证明：优化方法较之其他方法更有效率，准确率更高。

模糊分类系统； 模糊规则； 量子进化； 量子行为粒子群优化

0 引 言

模式分类是模式识别领域内最重要的研究方向之一，作用是将每一个输入量划分到合适的分类集合中。模式分类包含了分类系统设计和分类系统应用。在实际分类问题中，数据集往往包含了不确定性和噪声干扰,可能导致离散的分类方法不能准确地将数据分类到正确的集合当中。模糊集合与模糊逻辑理论为更灵活地分析数据集数据提供了一种连续分类方法[1,2]。例如，利用模糊规则进行分类系统设计被认为是一种很好的分类方法。这种方法贴近于人类日常的知识表达，所以可以用来设计出效率高、过程透明简单、解释性强的分类系统。在过去几十年里，模糊分类方法广泛地应用于包括过程控制[3]、项目决策[4]、信号处理[5]在内的各个研究和生产领域。

本文提出了一种新方法来改进模糊分类系统，即量子行为粒子群优化(quantum-behaved particle swarm optimization，QPSO)算法[6]。作为PSO算法的变式算法，QPSO算法因其强大搜索能力解决了很多优化问题。但对于多次应用在连续搜索空间问题，QPSO不能直接应用在一个由离散数据组成的优化问题当中。而模糊规则的优化恰属于离散问题。因此，文中将量子位[7]的概念结合到QPSO算法中，使之成为可以适用于离散问题的算法，并用此算法来改进模糊分类规则。在这种算法中，每个个体粒子被编组成独立的量子位。利用机器学习数据库中的数据集对上述算法进行了实验测试，验证了算法的有效性和准确性。

1 基于量子位表达和量子衍生粒子群算法的模糊分类系统

1.1 量子位表达理论

量子计算，信息由一个量子位表示，其中，单个量子位值可以表示0或1或两者的叠加。根据该信息的概率，叠加可能的状态既可以是0也可以是1。量子状态用波函数的希尔伯特空间构建[8]，定义如下

|Ψ〉=α|0〉+β|1〉

(1)

式中α和β为复数，用来指定相应状态的概率振幅。|α|2给出了该量子位将在“0”状态中找到的概率，|β|2给出了该量子位将在“1”状态中发现的概率[9]。量子状态的标准化要保证

|α|2+|β|2=1

(2)

1.2 QPSO算法

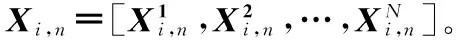
1.3 PSO的量子计算原理

PSO的应用已经扩展到量子计算领域，称为量子衍生粒子群优化(quantum-inspired particle swarm optimization，QiPSO)算法。 QiPSO的主要思想是用量子角度θ更新粒子位置。在常规的PSO中速度更新方程被修改可以得到一个表示量子位新概率的新的量子角度

Δθn=w×Δθn-1+c1×rand()×(θgbestn-θn)+

c2×rand()×(θpbestn-θn)

(3)

在特征变量选择中，每一个量子位用一个量子旋转角度θ定义来表示一个特征。在这种情况下，量子坍缩态的“1”值表示特征被选择，“0”值表示特征未被选择。

1.4 基于QiPSO和量子位表达的模糊分类系统优化

在模糊分类系统中，初始化操作构建了第一代种群粒子;确定输入空间划分基于随机的个体方法;模糊规则的类别输出标号和置信度依赖于计算输入空间中的训练数据。在接下来的每一次迭代计算过程中，QPSO算法划分每个输入空间并计算模糊规则的分类输出标号和置信度。

1)种群编码

一般的模糊分类系统直接根据专家经验或者实践经验构建模糊规则，虽然保证了一定的合理性，但很难达到快速建立分类系统的目的，而且对于比较复杂的研究对象，构建的分类系统会出现模糊规则较大冗余的情况。利用种群编码再进行量子选择可以避免上述问题。

量子进化算法中的每个种群个体包含了一个模糊分类系统中所有IF-THEN型模糊规则的前件，每个个体进行二进制编码后，均包含了特征分量控制部分和模糊划分控制部分，两部分共同作用对于输入数据的每个个体进行输入空间划分。

2)设定适应度函数

基于QiPSO和量子位表达的模糊分类系统的重点就是要寻找最优的个体，尽可能提高分类系统的分类正确率，即最大的正确分类样本的个数；同时也要使得模糊分类模型中含有较少的模糊规则个数。设定的适应度函数为

F(t)=w1×f1(t)+w2×Ns(t)+w3×Nr(t)

(4)

3)种群更新

在量子理论中，利用量子门变换矩阵来实现各个状态之间的转移，同时可以利用量子旋转门的旋转角度来完成染色体的变异过程，在变异的过程中可以产生新的个体，从而达到加快收敛的目的。在0/1编码的问题中，利用式(5)来设计量子更新算子

(5)

1.5 模糊分类系统优化算法步骤

采用QiPSO的方法对模糊分类系统进行设计，具体设计步骤如下：

1)对种群相应参数进行初始化设置包括算法的迭代代数G，种群的个数PopSize，输入变量位个数l，量子操作(量子旋转门角度θ)，重叠因子μ，适应度函数参数w1，w2和w3。

2)令g=1，随机产生第一代的初始种群个体。

3)令k=1，表示当前种群的第k个个体。

4)根据第k个个体的二进制编码确定模糊规则的特征分量个数和模糊划分个数，从而确定模糊规则数目。

5)由训练数据确定每条模糊规则的隶属度函数，从而确定模糊分类系统模型的IF-THEN型模糊规则的前件内容,即IF部分。

6)运用隶属度函数对训练数据进行相应的计算得出输出类别标号及置信度，从而确定模糊分类系统模型的IF-THEN型模糊规则的后件内容,即THEN部分。

7)记录该模糊分类系统模型的模糊规则数目，并利用测试数据来检验所建立的模糊分类系统模型能正确进行分类的数据个数。

8)根据适应度函数计算出第k个个体的适应度值。

9)令k=k+1，若k

10)令g=g+1，若g

11)利用量子操作(如量子旋转)来产生下一代的种群个体，然后跳至步骤(3)。

12)找出适应度值最高的种群个体，由具有最大适应度值的种群决定模糊规则库确定最终模糊分类系统模型。

2 实验与分析

为了测试算法的性能，选取了UCI机器学习数据库的3个数据集进行实验，分别为：1)比马糖尿病数据集Pima。2)文档页面模块数据集Blocks。3)心脏CT扫描图像数据集Hearts。从分类精确度、模糊规则数目同分类运行时间等指标入手，比较PSO的分类模型同其他算法优化的分类模型之间的性能优劣。

每个数据集都经过遗传算法(genetic algorithm,GA)、量子进化算法(quantum evolution algorithm,QEA)、QPSO算法的性能测试，测试参数设置为：PopSize=200，G=81，RunningTimes=11。算法结果如表1所示。

表1 模糊分类性能综合分析

从表1中可以看出:直接模糊分类系统建模的模型规则数据量比较大，初始模型的模糊规则数会随着属性个数的增加和输入变量的增加呈现指数性的增加。虽然所建模型的优点是精确性较高，但是解释性差，系统规模巨大，不适合实际的工程运用。利用PSO算法和量子化表达建立的模糊分类模型是在直接模型建模的基础上进行的优化过程，精简了初始分类模型的结构，提高了系统的运行效率，也使得模型的解释性得到提高。

3 结束语

本文重点研究了模糊分类系统的建模方法和实际工程的分类应用，主要内容包括量子化表达理论和群体智能算法在模糊分类系统中的具体应用，并对不同数据库进行仿真分类模拟，比较分类结果。根据实验结果分析出，利用量子化理论和PSO算法得出的模糊分类系统模型在保证分类精度的前提下，精简了系统结构，降低了模糊规则库规模，提高了分类模型的解释性，有较高的实际应用价值。

[1] Zadeh L A.Fuzzy logic[J].Computer,1988,21(4):83-93.

[2] Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.

[3] 谢黎明,查富生,李国慧.快速运动过程中双足机器人重心稳定的自适应模糊控制[J].机床与液压,2004(9):65-67.

[4] 赵振武,唐万生.基于模糊模拟的风险投资项目决策[J].模糊系统与数学,2007,21(4):150-155.

[5] 张国光.采用ZigBee和模糊PID控制的水声信号采集系统[J].舰船电子工程,2015(9):156-159.

[6] Sun J,Feng B,Xu W.Particle swarm optimization with particles having quantum behavior[C]∥2004 Congress on Evolutionary Computation,CEC2004,IEEE,2004:1571-1580.

[7] Prince J D.Quantum computing:An Introduction[J].Journal of Electronic Resources in Medical Libraries,2014,11(3):155-158.

[8] Han K H,Kim J H.Quantum-inspired evolutionary algorithm for a class of combinatorial optimization[J].IEEE Transactions on Evolutionary Computation,2002,6(6):580-593.

[9] Han K H,Kim J H.Genetic quantum algorithm and its application to combinatorial optimization problem[C]∥Proceedings of 2000 Congress on Evolutionary Computation,IEEE,2000:1354-1360.

OptimizationdesignoffuzzyclassifcationsystembasedonQPSO*

ZHU Yun-hui, SUN Jun

(SchoolofInternetofThingsEngineering,JiangnanUniversity,Wuxi214122,China)

An effective method for construction of fuzzy classification system(FCS)is proposed.In FCS,the initial fuzzy rules are optimized with a quantum bit which has many unique advantages such as small population size,fast convergence,short training time and strong global search ability.After then,in order to accomplish the optimization for the fuzzy classification space and reduce number of fuzzy rules,quantum-behaved particle swarm optimization(QPSO)algorithm is proposed to improve characteristics of initial FCS.The experimental result demonstrates that this method is more efficient and accurate than other methods without QPSO.

fuzzy classification system; fuzzy rules; quantum evolution; quantum-behaved particle swarm optimization(QPSO)

10.13873/J.1000—9787(2017)10—0089—03

2016—10—09

国家自然科学基金资助项目(61672263)

TP 391.4

A

1000—9787(2017)10—0089—03

诸云晖(1991-)，男，通讯作者，硕士研究生，主要研究方向为模式识别、模糊系统，E—mail:cloudhow10211@126.com。