金属壳谐振陀螺研究进展*

刘 宁， 苏 中， 李 擎

(高动态导航技术北京市重点实验室 北京信息科技大学，北京 100101)

金属壳谐振陀螺研究进展*

刘 宁， 苏 中， 李 擎

(高动态导航技术北京市重点实验室北京信息科技大学，北京100101)

金属壳谐振陀螺是振动陀螺的一个重要分支，其敏感结构为金属制成的壳体，称为金属谐振子，当谐振子随载体旋转时，哥氏效应引起敏感结构振型的“移动”是其对“旋转”敏感的基本表现形式。金属壳谐振陀螺不仅具有传统陀螺的惯性品质，而且具有能够抗高过载、量程大的特点，这是其他类型陀螺所不具备的。本文综述了金属壳谐振陀螺的研究进展，从设计思想、理论建模、结构设计、信号处理等方面进行了讨论，并指出了金属壳谐振陀螺的发展趋势。

金属壳谐振陀螺； 振动陀螺； 哥氏效应； 谐振子

0 引 言

金属壳谐振陀螺因其采用合金材料作为谐振子，具有结构强度高、抗过载能力强的优点，在兼顾抗过载、量程和精度上表现出了巨大的潜力[1～8]。文献[6,7]将金属壳谐振陀螺、半球谐振陀螺归属于固体波动陀螺范畴。金属壳谐振陀螺是目前能够有效解决大量程、高过载环境下角速率测量的重要传感器。国内对于该类型陀螺的研究与国外还有很大差距，且国内外对其大量程、抗高过载特性的研究已进入瓶颈。因此，急需从设计思想、理论建模、结构设计、信号处理等方面开展创新研究，研制出能够适应民用、军事等领域载体(钻探机构、弹丸等)大量程、高过载环境、结构简单的新型陀螺。下面分别对国内外研究现状加以分析。

1 国外金属壳谐振陀螺研究现状

1890年,英国著名物理学家Bryan G进行了轴对称壳谐振子的振动特性研究，奠定了金属壳谐振陀螺的理论基础，同时代的科学家Ralyeigh为描述谐振子的振型提供了数学分析依据[9]。美国从20世纪60年代便开始了相关振动陀螺的研制，20世纪90年代，Lynch D D对轴对称壳谐振陀螺提出了新的构想，使得该类陀螺的发展进入了快车道，形成了独特的陀螺理论分支[2,4]。在同一时期，苏联学者马特维耶夫等人也做了大量的研究工作，为轴对称壳谐振陀螺的发展奠定了坚实的基础[6,7]。

金属壳谐振陀螺的概念是进入21世纪后才被提及与归纳的[4，5]。金属壳谐振陀螺的发展，得益于半球谐振陀螺的研制。半球谐振陀螺虽然不属于金属壳谐振陀螺范畴，但其发展却时时影响着金属壳谐振陀螺。半球谐振陀螺是目前性能最高的轴对称壳谐振陀螺，已广泛应用于飞船与卫星的稳定控制、航天器导航、深海导航等领域，代表了轴对称壳谐振陀螺的最高水平。然而半球谐振陀螺采用熔融石英材料作为谐振子，采用静电激励和电容检测方式检测输入角速率，为了保证精度，采用力平衡工作模式，进行角度输出，其过载能力、量程均受到限制[10]。

最早的金属壳谐振陀螺是Marconi公司在20世纪80年代初研制的筒形波动陀螺，其产品代号为“START”，寓意为新的开始[11，12]，1987年制造出原理验证样机，1995年开始大批量生产。该陀螺的谐振子是圆柱形结构，其核心部件由压电电极、圆筒型谐振子和基座构成，如图1所示[6～8]。该陀螺谐振子采用了金属和石英2种材料，最终生产的为金属结构的谐振子。圆筒型陀螺的研制成功，使金属壳谐振陀螺从理论变成了现实。其自由端(即谐振子开口端)沿环向固定有8个压电电极，压电电极驱动谐振子自由端产生四波腹振型，在哥氏力作用下谐振子自由端振型产生进动，利用压电电极的压电效应提取进动量，最后利用电路系统解算输入角速率。该陀螺的研究过程，也为后续的金属壳谐振陀螺研制奠定了基础。据公开的文献报道，其最高分辨率可达到0.01°/s[6,12,13]。但是，由于压电电极紧贴自由端，影响了谐振子的刚度分布，导致模态干扰误差增大，稳定性、量程均受到限制，同时其抗过载能力受结构制约，仅能达到kgn水平。

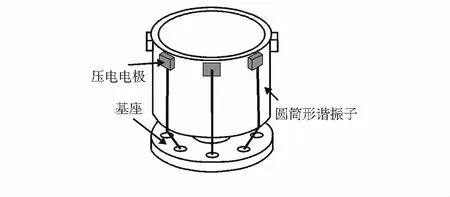
图1 “START”圆筒型陀螺

针对这种标准圆柱形结构形式的金属壳谐振陀螺，挪威学者Kristiansen D研究了这类振动陀螺的非线性振动模型与控制方法，给出了简化动力学模型，并通过谱分析手段对模型进行了验证[14]，阐述了圆柱形金属壳谐振陀螺的建模、分析与控制器设计[15]，但受限于当时的器件水平，Kristiansen D并未制作出样机，仅是在理论上给出了验证。弗吉尼亚理工大学学者Loveday P W同Kristiansen D一样，对这类陀螺的建模、控制器设计进行了研究[16]，但其研究的内容主要涉及以压电材料构成的圆柱形谐振陀螺[17]，针对有缺陷谐振子的建模与控制也进行了阐述，并对信号解算方法进行了研究与仿真验证，利用多回路控制手段抑制缺陷谐振子的频率裂解，显著提高了陀螺的整体性能[18]。上述两位学者，分别针对金属和压电谐振子系统阐述了圆柱形谐振陀螺的设计过程。而不同点在于，在谐振子模型建立方面，前者根据实验结果，利用Donnell-Mushtari理论和拉格朗日方法建立了谐振子振动过程中的非线性模型，而后者是利用Hamilton原理和Rayleigh-Ritz方法分析了耦合机电动力学的谐振子模型，并给出了边界条件；在信号处理方面，前者重点研究非线性观测器设计，并提出了针对这种二维振动系统的控制方式；而后者系统的阐述了多回路控制方法，利用速率解算回路输出角速率信息，同时利用正交控制回路抑制振子正交误差。两位学者只是在理论和研究思路上进行了创新，并未从工程实践角度提高圆柱形金属壳谐振陀螺的整体性能。

2004年，英国学者Kanani B在其1990年研究的基础上，制作出了一款大量程的圆柱形金属壳谐振陀螺(图2)，量程可达到800°/s[19]。与Marconi公司的产品相比，该款陀螺修改了结构尺寸和安装方式，其谐振子壁厚为2mm，底部厚度为10mm，外径21mm，整体高度30mm。由于提高了壁厚，同时增大了尺寸，使得谐振子整体弹性阻尼变强，增大了量程。但自此之后，Kanani B并未公开后续研究成果，该陀螺的其他指标也无法获知。可以肯定的是，Kanani B为金属壳谐振陀螺研制提出了新的方向，即调整结构来增大量程。

图2 Kanani B研制的金属壳谐振陀螺

美国Watson公司，也是较早研制该类陀螺的厂家，其研制的谐振子有压电陶瓷谐振子(图3(a)和图3(b))、金属壳谐振子(图3(c))，谐振子形式为圆柱形结构[20]。不同于“START”的是：金属壳谐振子的固定方式与结构形式不同。为避免前者稳定性差的不足，后者在进行压电电极粘贴时选择远离自由端的约束端进行布置，有效降低了模态间干扰，显著提升了整体精度。目前，Watson公司在售的金属壳谐振陀螺，零偏稳定性优于200°/h，标度因数稳定性优于300×10-6，量程不大于500°/s，抗过载性能达到500gn[21]。相比Marconi公司的金属壳谐振陀螺，并未有效提高精度、量程和抗过载能力等综合性能，且两者皆采用模拟量形式输出，其内部信号处理采用模拟电路方式实现，综合性能属于同一水平。

图3 Watson公司谐振子

著名陀螺专家Lynch D D利用平均方法给出了轴对称壳谐振陀螺的通用模型，模型中涉及刚度系数、阻尼系数、材料系数等一系列参数，为该类陀螺的推广奠定了基础[22]，使金属壳谐振陀螺研制真正进入了快车道[3]。其中，最有成效的是Innalabs公司，其通过将典型圆柱设计成两层结构，提高了谐振子刚性轴系上的刚度；同时将压电电极至于圆杯底部，降低了模态间耦合误差；利用Ni43CrTi合金材料提高了稳定性和灵敏度；研制了数控回路技术，有效的将振子控制与误差补偿有机结合，实现了陀螺的动态平衡和温度实时补偿，显著的提高了产品的性能[23～25]。目前Innalabs公司已有大量成熟产品，并广泛应用于无人机、无人车、制导炮弹、稳定平台控制等领域，其代表性产品及其组件如图4所示[26]。

图4 Innalabs公司的金属壳谐振陀螺组件

Innalabs公司经过多年的技术积累与创新，已经研制出目前综合性能最高的金属壳谐振陀螺,目前其典型陀螺性能指标对比如表1所示[26]。

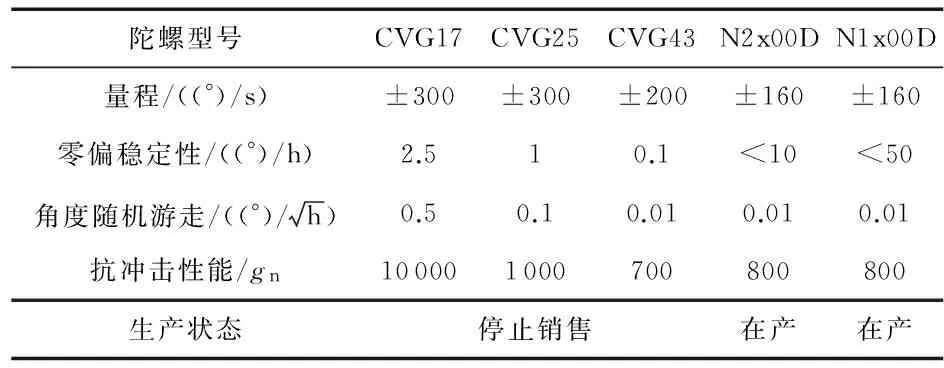
表1 Innalabs公司陀螺性能对比

虽然Innalabs公司的陀螺在抗高过载和精度方面的性能已经显著提高，相关研究已经达到了世界领先水平，但是受其结构特点影响，量程始终无法提高。

除此之外，2007年乌克兰科技大学的Bakalor T O等人，针对圆柱形金属壳谐振陀螺的高频控制问题，提出了一种低频结构的圆柱形金属壳谐振陀螺。其主要是在谐振子结构上进行修改，将壁厚变薄，从而降低了谐振频率，降低了电路设计的难度，从公开的资料中可以看出，其谐振子结构与Innalabs公司的谐振子基本一致，仅进行了细微调整，但该陀螺的其余性能指标均未见报道[27,28]。

图5 乌克兰科技大学的金属壳谐振陀螺

从20世纪90年代末到本世纪初期，吸引了大批学者对该陀螺进行研究，包括谐振子的理论建模、信号处理、测试评估和制造工艺等，形成了一套该类型陀螺的分析方法。在理论建模方面，主要围绕半球壳、圆柱壳和环形结构这类轴对称壳谐振陀螺进行研究，包括利用Donnell-Mushtari理论和拉格朗日方法建立谐振子振动的非线性模型[15]；利用Hamilton原理和Rayleigh-Ritz方法分析建立谐振子的机电耦合模型[18]；利用轨迹图法[29]、平均法[22]建立通用哥氏振动陀螺的数学模型；利用薄壳力学理论研究谐振子动力学方程并利用布勃诺夫—加廖尔金法进行求解，得到简化动力学方程[6,7,29]；分析布朗效应与各项同性非线性阻尼的关系并和本征值问题[30,31]，利用试验数据进行模型参数辨识[32]等。同时对谐振子的频率裂解问题展开研究，分析频率裂解产生的原因、误差传播的特性以及抑制方法[33～35]。在信号处理方面，首先提出了基于幅度控制回路、频率控制回路、正交控制回路和速率解算回路的多回路控制方法[18,24,25]；在此基础上，提出了利用先进控制理论，对这类陀螺的强耦合特性进行分析与求解[36]。

随着MEMS技术和材料科学的发展，有大量学者将轴对称壳与MEMS相结合，研制出了立体圆环结构[37,38]、圆柱形结构[39]、半球壳结构[40]、蜂窝鸟巢结构的MEMS陀螺；同时，也有学者通过改用高Q值高纯度单晶蓝宝石结构制作谐振子[41]，但由于材料上的特点，决定了该结构谐振子加工制造上的难度。工艺和材料上的新变革，拓展了金属壳谐振陀螺的新方向，然而仅通过这两项革新，仍然不能从根本上增大量程，提高抗过载能力，还需结构上、理念上的根本创新。

综上所述，国外对于金属壳谐振陀螺进行了多方位研究，已积累了大量的经验，形成了完整的研究体系。但是从公开的文献来看，在大量程、抗高过载方面，并没有太大进展，急需一种新结构形式的金属壳谐振陀螺，从本质上来提高这类陀螺的大量程、抗高过载性能。

2 国内金属壳谐振陀螺研究现状

与国外相比，我国相关研究起步较晚，在金属壳谐振陀螺范畴内至今未有成熟产品面世，许多研究工作只处于理论分析或实验室验证阶段。清华大学、复旦大学、浙江大学、哈尔滨工业大学、东南大学、哈尔滨工程大学、国防科技大学、中电26所、航天三院33所、北京航空航天大学、北京理工大学、南京理工大学等机构，是国内振动陀螺研究的中坚力量，目前研制成功有MEMS陀螺、石英音叉陀螺、半球谐振陀螺，代表了国内谐振陀螺研制的最高水平，为研制金属壳谐振陀螺积累了宝贵经验[42～50]。

国内最早报导的金属壳谐振陀螺研究，是北京航空航天大学樊尚春等学者。在20世纪80年代末90年代初，就开展了相关研究，但当时研究重点均围绕在壳体模型的分析上，其先后分析了谐振筒[51]、半球壳、缺陷半球壳、圆柱壳[52,53]等轴对称壳的理论建模、振型特性以及进动特性，开辟了国内该项研究的先河。同时，创新性地提出了变厚度轴对称壳谐振子的概念，并给出了传统轴对称壳、变厚度轴对称壳的近似解析公式，对谐振子的固有频率、振型、进动特性均作了统一分析。在对谐振子的结构设计、有限元仿真分析、信号处理、试验测试等方面也进行了大量探索。在理论建模方面，利用传统的薄壳力学思想和弹性力学中的能量原理相结合，提出了一种适用于轴对称壳动力学分析的全新方法；在仿真分析方面，率先在国内利用有限元方法分析了该类陀螺谐振子；在试验测试方面，提出了利用He-Ne激光器方法，得出谐振子的全息干涉图来谐振子的振型，这些研究为我国金属壳谐振陀螺的研究奠定了坚实的基础。

2013年，樊尚春教授出版了专著《轴对称壳谐振陀螺》，系统的对这类陀螺的发展与研究过程进行了总结，同时给出了近年来的相关试验验证结果[4]。

此外，国防科学技术大学吴学忠及其研究团队，也进行了大量的研究，已研制出多款陀螺样机。其早期研制的杯形波动陀螺(图6)，主体结构与Innalabs公司的金属壳谐振陀螺类似，谐振子均是典型的底部开孔式圆柱壳，壁上分为两级结构，将压电电极粘贴于杯形底部[28,54]。建立了杯形波动陀螺的数学模型，利用Ansys有限元分析软件分析了谐振子的振动特性，利用激光测振仪测试了谐振子振动幅值与振型；提出了利用谐振环顶部沿圆周方向开修形槽方式进行机械平衡调节，将频率裂解控制在0.01 Hz以内[54]。

图6 杯形波动陀螺

在此基础上，国防科学技术大学于2011年提出了一种新型环形振动陀螺(图7)，该陀螺靠8根粘贴有压电电极的隔离柱，支撑起谐振环振动，同时再利用隔离柱上的压电电极检测谐振环的振动。这种结构显著提高了杯形谐振陀螺的量程[55]。

图7 新型环形波动陀螺

同年，该项目组又提出了一种组合式谐振陀螺(图8)，利用金属壳和石英材料构成了组合式的结构，显著提高了陀螺的灵敏度，但其线性度指标明显降低[56，57]。

图8 组合式石英圆柱壳体振动陀螺

在后续研究中，重点针对典型的杯形波动陀螺进行研究，相继提出了杯形波动陀螺的品质因数分析[58]、振型偏移角快速辨识、谐振子结构参数优化等特性分析方法；同时还对其误差因素进行了研究，包括压电电极粘接胶层、温度[59]、谐振子加工缺陷等人[60]误差源特性分析与抑制；在谐振子测试方面，提出了利用声学传播方法分析谐振子模态参数[61]、利用MEMS声传感器进行振型检测[62]等先进的测试方法；在信号处理方面，在传统电路基础上，设计了高稳定度正弦驱动电路，并对测控系统进行了数字化改造[63]；在材料改进方面，提出了利用单晶金刚石研制微杯形谐振子的激光刻蚀制造方法[64]。该项目组近年研制的金属壳谐振陀螺具体指标如表2所示。可以看出，陀螺的零偏稳定性已能满足基本应用，达到了国际同类水平；但量程相对较低，仅能适用于低转速领域；抗过载能力，在研制过程中均未提及具体指标。

2010年至今，北京理工大学、北京信息科技大学研究团队受中国传统大钟启发，与金属壳谐振陀螺设计思想相结合，创新性的提出了一种能够满足高动态环境下使用的钟形振子式角速率陀螺，并对其抗高过载、大量程设计进行研究，成功研制出样机[65]。该陀螺与loper E J等人所提出的钟形陀螺具有本质区别，loper E J等人当时提出的“Bell”形陀螺只是半球谐振陀螺的一种结构形式，采用熔融石英加工的半球壳形式作为谐振子，在申请了3项专利之后，未见后续报导[66]。

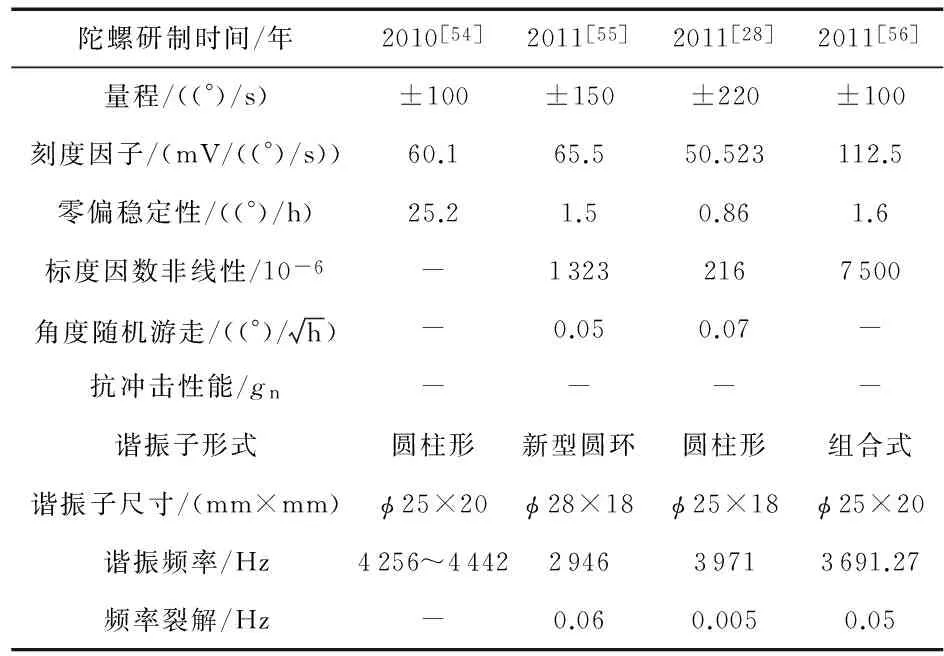
表2 国防科学技术大学杯形波动陀螺指标汇总

总而言之，国内对于金属壳谐振陀螺的研究虽然起步较晚，但也取得了一些进展。首先在结构形式上，紧跟国际步伐，研制出基本结构形式的金属振子；在陀螺精度上，研制出的样机已经达到了国际同类水平。

3 结束语

综合国内外金属壳谐振陀螺的研究现状可以看出，目前该类陀螺的抗高过载能力已得到国内外同仁广泛认可，其发展趋势在于如何兼顾量程、过载和精度。在研究过程中，还面临如下问题：

1)在总体性能方面，现有圆柱形、改进的圆柱形、立体圆环形等结构在综合量程、抗过载能力上和精度上没有达到要求，精度已经能够满足角速率检测需求，但量程最大仅为800°/s，过载最大为10 000gn，无法满足大量程、高过载环境应用。

2)在结构设计方面，现有结构选取方法仅是通过分析结构参数、材料参数变化，找到合适参数，没有进行系统性的优化分析，所得到的参数不一定是最优值，影响了谐振子的振动特性，限制了陀螺的量程。

3)在信号处理方面，现有的信号处理方法，没有考虑回路间控制信号耦合问题，所提出的先进控制解算方法，没有针对金属壳谐振陀螺进行设计，控制精度不理想，制约了陀螺精度。

[1] Mario N A,Caterina C,Francesco D,et al. Advanced in gyroscope technologies[M].Berlin:Springer,2013:1-30.

[2] Lynch D D.Coriolis vibratory gyros[C]∥Proceedings of the Symposium Gyro Technology,1998.

[3] IEEE 1431—2004.IEEE standard specification format guide and test procedure for coriolis vibratory gyros[S].New York:Institute of Electrical and Electronics Engineers,2014.

[4] 樊尚春.轴对称壳谐振陀螺[M].北京:国防工业出版社,2013.

[5] 刘 宇.固态振动陀螺与导航技术[M].北京:中国宇航出版社,2010.

[6] 马特维耶夫B A,利帕特尼科夫B И,阿廖欣A V,等.固体波动陀螺[M].杨亚非,赵 辉,译.北京:国防工业出版社,2009.

[7] Mатвеев B A,Лунин Б С,Басараб M A.固态波陀螺仪导航系统[M].马菊红,译.哈尔滨:哈尔滨工业大学出版社,2013.

[8] Shkel A M.Type I and type II micromachined vibratory gyro-scopes[C]∥2006 Position,Location,and Navigation Symposium,IEEE/ION,2006:586-593.

[9] Bryan G.On the beats in the vibrations of a revolving cylinder or bell[C]∥Proceedings of the Cambridge Philosophical Society,1890.

[10] 方 针,余 波,彭 慧,等.半球谐振陀螺技术发展概述[J].导航与控制,2015,14(3):2-7.

[11] Langdon R M.The vibrating cylinder gyroscope[J].The Marconi Review,1982(45):231-249.

[12] Ander J,Pearson R.Application of the“START”vibratory gyroscope[J].GEC Review,1994(9):168-175.

[13] 胡爱民.微声电子器件[M].北京: 国防工业出版社,2008:178-180.

[14] Kristiansen D,Egeland O.Nonlinear oscillations in coriolis-based gyroscopes[J].Nonlinear Dynamics,1999,19(3):193-235.

[15] Kristiansen D.Modeling of cylinder gyroscopes and observer design for nonlinear oscillations[D].Norway:Norwegian University of Science and Technology,2000.

[16] Loveday P W,Rogers C A.Free vibration of elastically supported thin cylinders including gyroscopic effects[J].Journal of Sound & Vibration,1998,217(3):547-562.

[17] Loveday P W，Rogers C.Modification of piezoelectric vibratory gyroscope resonator parameters by feedback control[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,1998,45(5):1211-1215.

[18] Loveday P W.Analysis and compensation of imperfection effects in piezoelectric vibratory gyroscopes[D].Virginia:Virginia Polytechnic Institute and State University,1999.

[19] Kanani B.Operating principles of the monolithic cylinder gyroscope[C]∥2004 IEEE Ultrasonics Symposium,2004:1195-1198.

[20] Watson W S.Vibrating inertial rate sensor utilizing skewed drive or sense elements:USA,US 7526957[P].2009—05—05.

[21] Watson Industries Inc.Pro gyro spec sheet[EB/OL].[2015—03—05].http:∥watson-gyro.com.

[22] Lynch D D.Vibratory gyro analysis by the method of avera-ging[C]∥Proc of The 2nd St Petersburg Conf on Gyroscopic Tech-nology and Navigation,St.Petersburg.1995:26-34.

[23] Chikovani V V,Yatzenko Y A,Kovalenko V A.Coriolis force gyroscope with high sensitivity:USA,US7513156[P].2009—04—07.

[24] Chikovani V V,Yatsenko Y A,Barabashov A S,et al.Improved accuracy metallic resonator CVG[J].IEEE Aerospace and Electronic Systems Magazine,2009,24(5):40-43.

[25] Okon I M,Simonenko D V,Barabashov A S.Sensing element of Coriolis force gyroscope:USA,US721228[P].2010—03—10.

[26] Innalabs Technologies,Inc.High performance ITAR-free gyro-scopes[EB/OL].[2015—09—15].http:∥www.innalabs.com.

[27] Bakalor T O,Bondar P M.Research of a low-frequency spectrum of resonators Coriolis vibrating gyroscope[C]∥Movement Control and Aerospace Technic Engineering,Ukraine,2007:110-114.

[28] 陶 溢.杯形波动陀螺关键技术研究[D].长沙:国防科学技术大学,2011.

[29] Apostolyuk V,Gorbunovich I.Mathematical model of Coriolis vibratory gyroscopes motion trajectory[J].Редакц?йна колег?я,2010(5):39-42.

[30] Joubert S V,Shatalov M Y.Manzhirov A V.Bryan’s effect and isotropic nonlinear damping[J].Journal of Sound and Vibration,2013,332(23):6169-6176.

[31] Joubert S V,Shatalov M Y,Fay T H.On numerically solving an eigenvalue problem arising in a resonator gyroscope[J].Applied Mathematics and Computation,2014,246:561-571.

[32] Shatalov M Y,Lunin B S.Vibratory gyroscopes:Identifica-tion of mathematical model from test data[C]∥The 14th International Conference on Integrated Navigational Systems(ICINS),2007.

[33] Shatalov M Y,Joubert S V,Coetzee C E.The influence of mass imperfections on the evolution of standing waves in slowly rotating spherical bodies[J].Journal of Sound and Vibration,2011,330(1):127-135.

[34] Choi S Y,Kim J H.Natural frequency split estimation for inextensional vibration of imperfect hemispherical shell[J].Journal of Sound and Vibration,2011,330(9):2094-2106.

[35] Lynch D D.CVG’s utilizing non-axisymmetric structures opera-ting in whole-angle mode[C]∥2014 International Symposium on Inertial Sensors and Systems(ISISS),IEEE,2014:1-4.

[36] Leland R P.Adaptive tuning for vibrational gyroscopes[C]∥IEEE Conference on Decision and Control,IEEE,2001:3447-3452.

[37] Abdul-wahed A M,Mahmoud M A E.Vibratory ring six-axis motion sensor[J].Microsystem Technologies,2014,21(10):1-12.

[38] Yoon S.W,Lee S,Najafi K.Vibration sensitivity analysis of MEMS vibratory ring gyroscopes[J].Sensors and Actuators A:Physical,2011,171(2):163-177.

[39] Desta Y M.Fabrication of high aspect ratio vibrating cylinder microgyroscope structures by use of the liga process[D].Louisiana:Louisiana State University,2005.

[40] Senkal D,Ahamed M J,Trusov A A,et al.Electrostatic and mechanical characterization of 3D micro-wineglass resonators[J].Sensors and Actuators A:Physical,2014,215:150-154.

[41] Sergii A,Sarapuloff.High-Q single-crystalline resonator fabrica-tion of CRG-1 for inclinometry of oil & drilling[J].Special Technologies & Machines,2009,1(2):101.

[42] 陈泓伍,陈玺浩,彭 晨,等.全对称振动陀螺的结构设计与参数优化分析[J].仪表技术与传感器,2014(12):1-4.

[43] 许 昕,何 杰,王 文,等.微机械陀螺仪的新进展及发展趋势[J].压电与声光,2014,36(4):588-595.

[44] 姜 萌,冯巧玲,梁同利,等.基于增强石英音叉的光声探测器研究进展[J].激光与光电子学进展,2015,52(9):11-20.

[45] 余 磊,徐大诚,郭述文.硅微角振动陀螺仪温度特性补偿方法研究[J].传感器与微系统,2016,35(11):26-29.

[46] 朱 京,温廷敦,许丽萍,等.基于介观压光效应的MEMS陀螺研究[J].传感器与微系统,2015,34(3):15-17,20.

[47] 韦 念,吴校生,刘 武,等.压电微固体模态陀螺的安装技术[J].传感器与微系统,2015,34(10):41-43,53.

[48] 刘弘毅,宋来亮,张春熹.三轴一体IMU组件中光纤环热分析[J].传感器与微系统,2016,35(6):9-12,16.

[49] 李丽锦,汤恒先,周志广,等.框架式垂直陀螺仪误差特性研究[J].传感器与微系统,2015,34(12):51-53.

[50] 高胜利,吴简彤.半球谐振陀螺的漂移机理及其控制[J].弹箭与制导学报,2008,28(3):61-64.

[51] 刘广玉,樊尚春.压电激励谐振筒压力传感器的研究[J].仪器仪表学报,1988,9(2):134-140.

[52] 樊尚春,刘广玉.圆柱壳角速率敏感器实际结构设计[J].北京航空航天大学学报,1996,22(4):397-401.

[53] 樊尚春,刘广玉.圆柱壳角速率敏感器耦合振动的近似解析分析[C]∥中国自动化学会第十三届青年学术年会，张家界， 1998：226-229.

[54] 吴学忠,陶 溢,崔红娟,等.杯形波动陀螺的杯形谐振子及其机械平衡方法:中国,201010203042.7[P],2010—09—29.

[55] Tao Y,Wu X Z,Xiao D B,et al.Design,analysis and ex-periment of a novel ring vibratory gyroscope[J].Sensors and Ac-tuators A:Physical,2011,168(2):286-299.

[56] 栾清磊.组合式石英圆柱壳体振动陀螺的研究[D].长沙:国防科学技术大学,2011.

[57] 吴宇列,吴学忠,崔红娟,等.组合式石英杯形波动陀螺谐振子:中国,201110190891.8[P].2011—07—08.

[58] Xi X,Wu X,Zhang Y,et al.A study on Q factor of the trimmed resonator for vibratory cupped gyroscopes[J].Sensors and Actuators A:Physical,2014,218:23-32.

[59] Xi X,Wu Y,Wu X,et al.Modeling and analysis of the stress effects for trimmed cupped resonator under varying tempera-ture[J].Sensors and Actuators A:Physical,2013,189:429-440.

[60] 朱炳杰.杯形陀螺谐振子振动特性分析及修整技术研究[D].长沙:国防科学技术大学,2011.

[61] Xi X,Wu X,Wu Y,et al.Structural-acoustic coupling effects on the non-vacuum packaging vibratory cylinder gyroscope[J].Sensors,2013,13(12):17176-17192.

[62] Zhang Y,Wu Y,Wu X,et al.A novel vibration mode testing method for cylindrical resonators based on microphones[J].Sensors,2015,15(1):1954-1963.

[63] 谢 笛.杯形波动陀螺数字化测控技术研究[D].长沙:国防科学技术大学,2011.

[64] 何汉辉,李 微,肖定邦,等.单晶金刚石微杯形谐振子的激光刻蚀制造方法[J].强激光与粒子束,2015,27(2):14-18.

[65] Liu Ning,Su Zhong,Li Qing.Design and experiment of a novel bell-shaped vibratory gyro[J].Sensors and Actuators A:Physics,2016,238:37-50.

[66] Loper E J,Lynch D D.Sonic vibrating bell gyro:USA,US4157041[P].1979—06—05.

Researchprogressofmetalsheelvibratorygyro*

LIU Ning, SU Zhong, LI Qing

(BeijingKeyLaboratoryofHighDynamicNavigationTechnology,BeijingInformationScience&TechnologicalUniversity,Beijing100101,China)

Metal shell vibratory gyro is an important branch of vibratory gyroscope,the sensitive structure of metal shell is called metal resonatro,when resonator rotate with vector,mobility of resonator caused by the Coriolis effect is the basic form of “spin” sensitive. Metal shell vibratory gyroscope not only has traditional gyro inertia quality,but also has features of characteristics that can resist high overload,and has large range ,this is what other types of gyro do not have.Research progress of metal shell vibratory gyroscope is reviewed,from design idea,theory modeling,structure design,signal processing,etc,are discussed,and development trend of metal shell resonant gyroscope are pointed out.

metal shell vibratory gyro; vibratory gyro; Coriolis effect; resonator

10.13873/J.1000—9787(2017)10—0004—06

2016—08—18

国家自然科学基金资助项目(61471046)；北京市教委市属高校创新能力提升计划资助项目(TJSHG201510772017)；高动态导航技术北京市重点实验室开放课题项目

TQ 028.1

A

1000—9787(2017)10—0004—06

刘 宁(1986-)，男，通讯作者，博士，助理研究员，从事高动态惯性器件、组合导航算法以及环境力测量研究工作，E—mail:nng.liu@bistu,edu.cn。