正交空间调制系统的低复杂度检测算法

陈发堂，刘 燕，李玉河

(重庆邮电大学 重庆市移动通信技术重点实验室，重庆 400065)

正交空间调制系统的低复杂度检测算法

陈发堂，刘 燕，李玉河

(重庆邮电大学 重庆市移动通信技术重点实验室，重庆 400065)

正交空间调制(quadrature spatial modulation, QSM)作为一种扩展的空间调制(spatial modulation, SM)传输方案，近年来受到业界的广泛关注。它通过在发送端将发送的复值符号的实部和虚部分开传输来提高频谱效率。由于正交空间调制系统的最大似然(maximum likelihood, ML)检测算法在整个搜索空间进行穷搜索，导致计算复杂度极高。针对QSM系统接收端检测算法复杂度较高的问题，利用QSM系统信号固有的稀疏特性，提出了一种QSM系统的压缩感知(compressed sensing, CS)检测算法。仿真结果表明，新的检测算法在误码性能上接近ML检测算法，复杂度约为ML的4.7%。

正交空间调制；检测算法；低复杂度；压缩感知

0 引 言

随着通信技术的不断发展，第五代通信系统(5 generation, 5G)需要满足多种终端设备同时接入和多样化的业务需求，并且达到系统频谱效率与能源效率的平衡，最终实现真正的绿色通信[1]。传统MIMO(multiple input multiple output, MIMO)系统发送端通过激活所有可用的天线同时传输多个数据流，并且选择适当的预编码矩阵，以实现信息复用或者发射分集增益[3]。这种方案虽使系统频谱效率提高，但系统并没有达到最佳的能源效率，并且存在许多弊端。而空间调制(spatial modulation, SM)[2]方案独创性地将发送信息映射到输入比特与发射天线上，在获得较高的频谱效率与系统性能的同时，能够有效地克服传统MIMO技术的弊端。

2001年，“空间调制”的编码原则在文献[4]中被首次提出，并被称为空移键控(space shift keying, SSK)调制，它是利用不同天线接收到的信号差异来区别不同的传输信息。2004年，S. Song等人提出了一种“信道跳变”技术[5]中输入信息的一部分用于空间星座点的映射，另一部分用于选取发送天线索引传输信息，这种传输方案被称为空间调制的MIMO系统(spatial modulation-MIMO, SM-MIMO)。直到2006年，Mesleh等人在文献[2]的研究基础上，第一次使用“空间调制”的术语来定义该种编码机制。为了进一步提高系统频谱利用率，文献[6]提出了激活多根发送天线的广义空间调制(generalized spatial modulation, GSM)方案，该方案中系统发送端通过激活至少2根天线来发送数据。随后人们又提出一种新颖的高频谱效率的正交空间调制(quadrature spatial modulation, QSM)方案，系统通过在发送端激活一根或两根天线分别用来发送星座符号的实部和虚部来提高频谱效率[7]。在传统SM系统中，每一时隙只使用单射频链路来避免信道间干扰(inter-channel interference, ICI)问题。而在高频谱效率的GSM系统中因为每一时隙激活多个天线来发送数据，所以存在ICI问题。但在QSM系统中，每一时隙激活天线发送的调制符号实部和虚部是正交的，所以QSM系统在提高系统频谱利用率的同时也避免了ICI问题[7]。

QSM的优势逐渐受到学者们的关注，而在系统接收端如何正确恢复出发送端的原始数据不同于传统MIMO系统接收端的解调。QSM系统特殊的映射方式，使得系统的解调变得困难。在当前现有的检测算法中，文献[7]中实现了QSM系统中最优检测即最大似然(maximum likelihood, ML)检测算法，但是该算法联合搜索所有可能的发射天线组合和调制符号导致计算复杂度极高。文献[8]中提出了一种基追踪降噪算法，并且取得较好的误码性能，但该算法计算复杂度还有待降低。同时该文献将迫零检测算法(zero-forcing, ZF)应用在QSM系统中，ZF算法以牺牲系统性能为代价换取较低计算复杂度。文献[9]中提出一种信号矢量基最小均方误差检测算法(signal vector based minimum mean square error, SVMMSE)，该算法将SVD和OB-MMSE结合，需在接收端先判断出发送端激活天线个数。如果判断发送端激活单根天线，则采用SVD检测算法；如果判断发送端激活两根天线，则采用OB-MMSE检测算法。仿真结果表明SVMMSE算法有较好的误码性能，且计算复杂度较低，但该算法在每次检测时都需要计算SVD和OB-MMSE两种算法。

最近，基于压缩感知(compressed sensing, CS)[10]稀疏信号重构理论被广泛应用在大规模天线系统中，因为其在信号检测方面有着极低的计算复杂度。许多学者利用GSM系统中信号的稀疏性将一些经典的CS算法应用在其中，比如正交匹配追踪(orthogonal matching pursuit, OMP)算法[11]，基追踪(basis pursuit, BP)算法[12]，压缩采样匹配追踪(compressive sampling matching pursuit, CoSaMP)算法[13]等。但是以上基于CS理论的算法都是在每一时隙激活天线数固定即信号稀疏度固定的GSM系统中实现的，并取得次于排序块最小均方误差算法(OB-MMSE)[14]和改进的OB-MMSE(IOB-MMSE)[15]的误码性能。然而QSM系统中发送端在每一时隙激活的发射天线数是在1和2之间根据输入的不同信息流变化的。文献[8]中将基追踪降噪算法应用在QSM系统接收端，虽然取得较好误码性能，但仍具有较高的计算复杂度。

本文充分利用QSM系统发送端信号固有的稀疏性的特点，结合CS理论中的OMP算法进行改进推广，从而提出新的检测算法。本文提出的次优算法有望在大规模天线空间调制系统中，成为性能与计算复杂度之间折中的有效方案。

1 正交空间调制系统模型

QSM系统模型如图1所示，发送天线数和接收天线数分别为Nt，Nr，数字调制符号为M阶传统星座图(M-QAM或M-PSK)的系统。

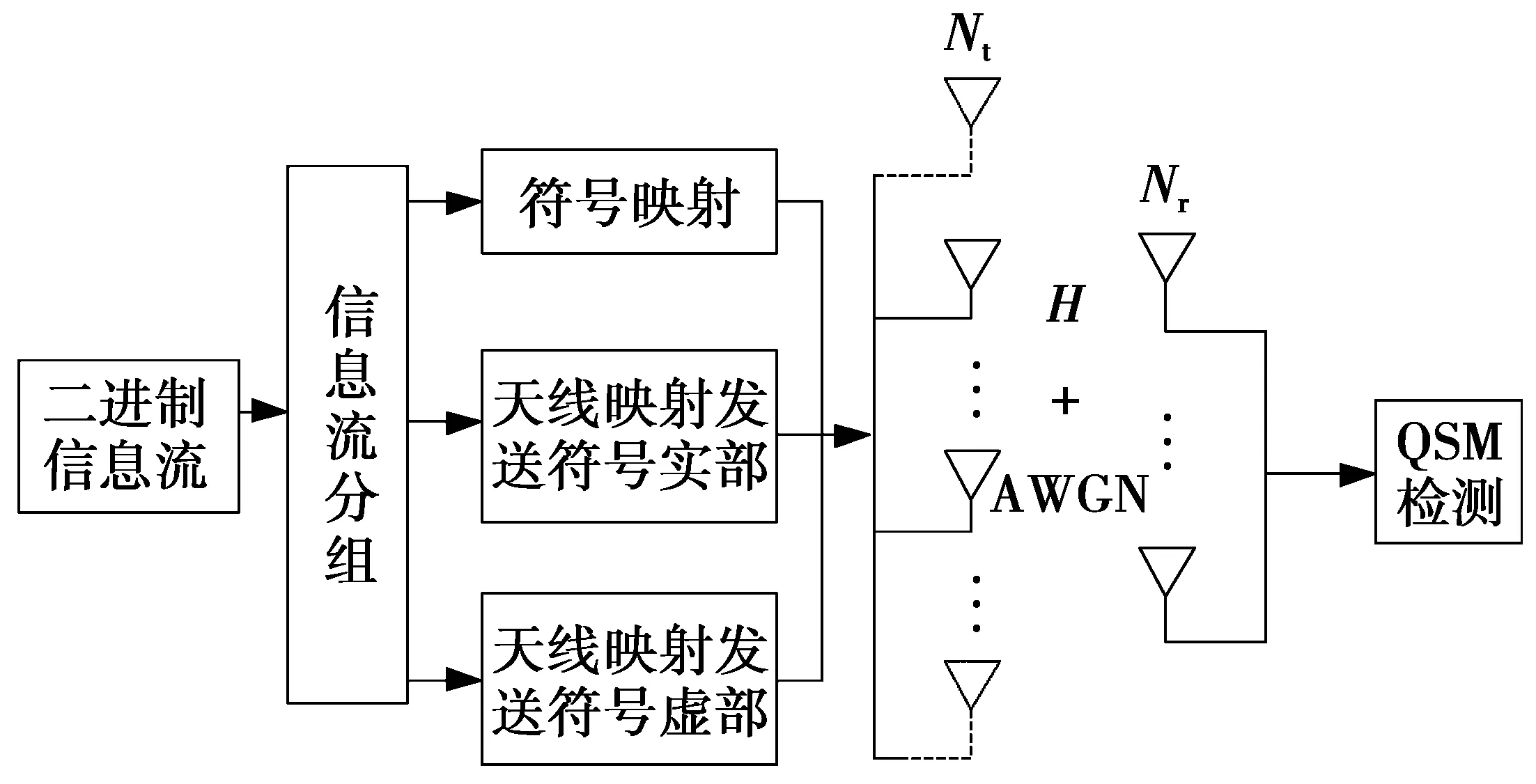
图1 QSM系统模型Fig.1 QSM system model

为了更清楚地阐述QSM系统的调制原理，考虑一个有4根发送天线3根接收天线的4QAM调制系统。当前发送端输入一组长度为R=6的信息比特为010110，第1部分01用来确定4QAM调制符号的第2个符号(1+i)被发送(如表1方式映射)，第2部分01用来选择第2根发送天线发送调制符号的实部(1)(如表2方式映射)，第3部分10用来选择第3根发送天线发送调制符号的虚部(i)(如表2方式映射)。

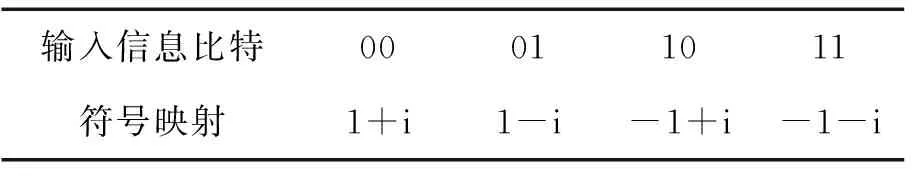
表1 调制符号映射

表2 天线索引映射

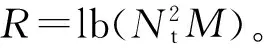
1)发送调制符号实部的天线索引lR大于发送虚部的天线索引lI时

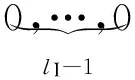
(1)

2)发送调制符号实部的天线索引lR等于发送虚部的天线索引lI时

(2)

3)发送调制符号实部的天线索引lR小于发送虚部的天线索引lI时

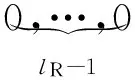
(3)

(1)—(3)式中：lR=(1,…,Nt)，lI=(1,…,Nt)。对于QSM系统，发送向量x∈Nt×1中只有1个或者2个元素为非零值。

令H∈Nr×Nt表示信道传输矩阵，n∈Nr×1表示加性高斯白噪声。H为服从均值为0，方差为1的复高斯随机变量，则H具有有限等距性(restricted isometric property,RIP)特性。n为独立同分布且均值为0，方差为δ2的复高斯随机变量。则QSM系统接收端的接收向量y∈Nr×1为

y=Hx+n=hlRsR+jhlIsI+n

(4)

(4)式中：hlR，hlI分别表示信道矩阵H的第lR列和第lI列。

对于QSM系统接收端检测，传统ML算法需要联合检测激活天线索引和数字调制符号的实部和虚部，数学表达式为

(5)

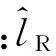
2 基于信号稀疏性的检测算法

通常采用凸松弛算法和贪婪算法来求解信号的稀疏问题。文献[8]中将凸松弛算法中的基追踪(BP)降噪算法应用在QSM系统中，用l1范数替代l0范数并结合QSM系统信号的特点来恢复出原始信号。然而对于一般的观测矩阵，凸松弛算法仍具有非常高的计算复杂度。贪婪算法比凸松弛算法具有比较低的复杂度，故本文主要将贪婪算法中的OMP算法进行改进推广并结合QSM系统信号的特点来进行信号检测。

从QSM系统发送端向量x∈Nt×1的表达式(1)式、(2)式及(3)式，可以看出其中少数元素不为零，具有稀疏性。故在QSM系统接收端的信号检测可以使用CS中的稀疏信号中重构算法来恢复出QSM系统发送端的原始信号。目前，成熟的CS理论都是在实数域展开的，在开始稀疏重构算法之前对基于复数域的QSM系统中接收向量变形，得到

(6)

(6)式中：R(·)和I(·)表示取变量的实部和虚部。(6)式等价为

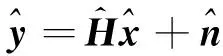
(7)

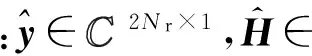
对于R(x)和I(x)表示取数字调制符号s的实部和虚部，展开得

(8)

(9)

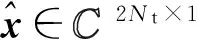
2.1 传统OMP算法的QSM信号检测

传统OMP算法。

2)fort=1:2

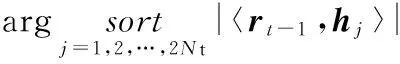
end

2.2 新的基于OMP算法的QSM信号检测

由于传统的OMP算法在每一次迭代过程中只取一个与当前残差相关最大的值作为天线索引，当接收信号受到深度衰落时，极大可能地搜索到错误的天线索引作为最终检测结果。从而导致在QSM系统的接收端采用传统OMP算法进行检测时，系统的误码性能较差。

本文提出算法。

2)fort=1:2

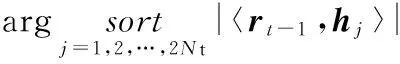
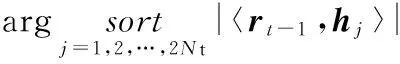
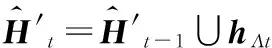
end

3)分别从集合Λ1，Λ2中取一个天线索引号进行组合，共S2种天线组合存入集合Γ

3 性能仿真与复杂度分析

本文对ML算法、OMP算法、BP算法[12]、及OB-MMSE算法[14]在相同信道环境和频谱效率下进行蒙特卡洛仿真，得到不同QSM系统参数配置下的误码性能。

3.1 仿真结果分析

仿真结果如图2和图3所示。图2的仿真参数为Nt=32，Nr=16，4QAM调制。图3的仿真参数为Nt=64，Nr=16，4QAM调制。其中S表示在每次迭代过程中选择的天线索引个数。

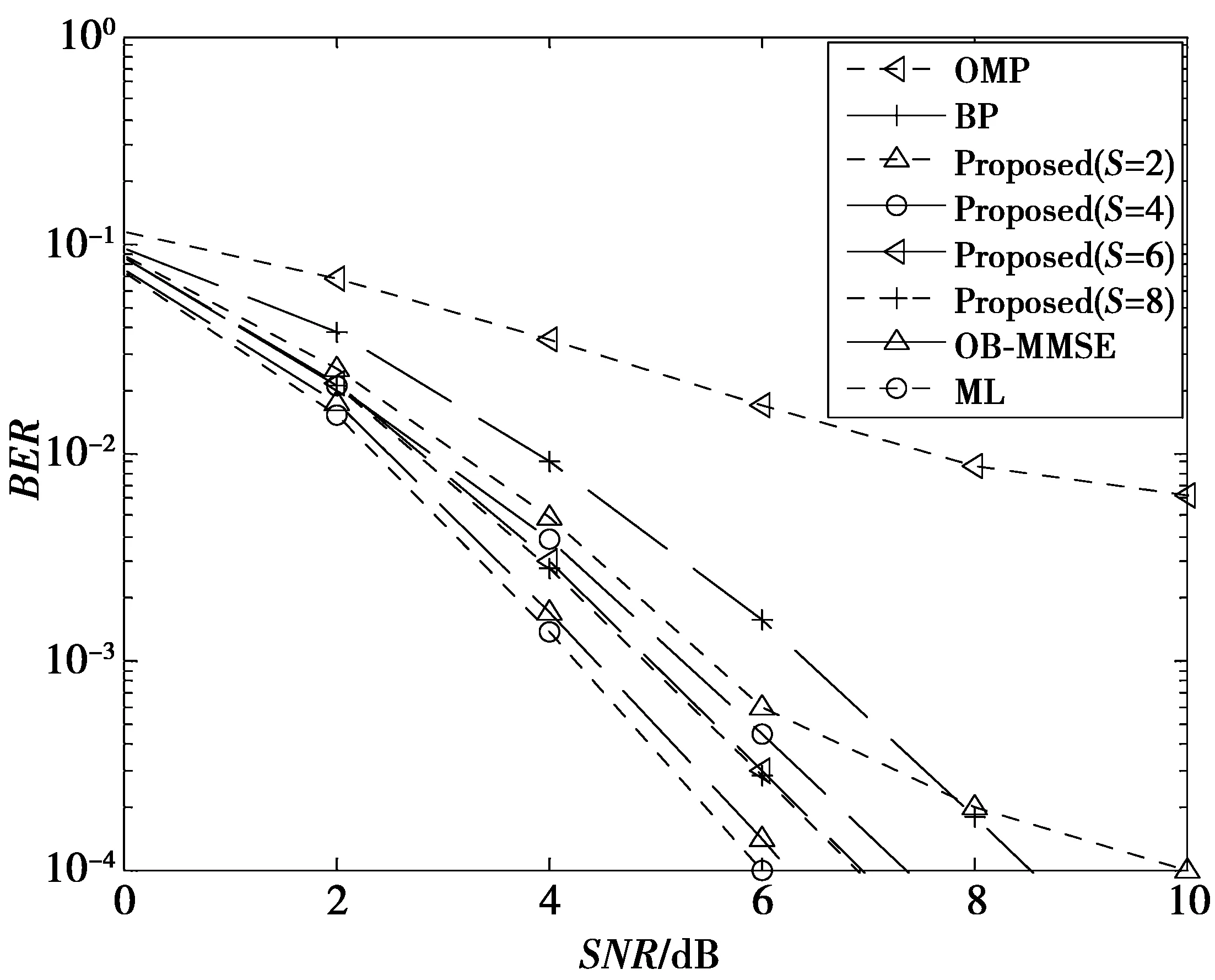
图2 QSM系统BER性能比较图(Nt=32)Fig.2 BER performance comparison of QSM system(Nt=32)

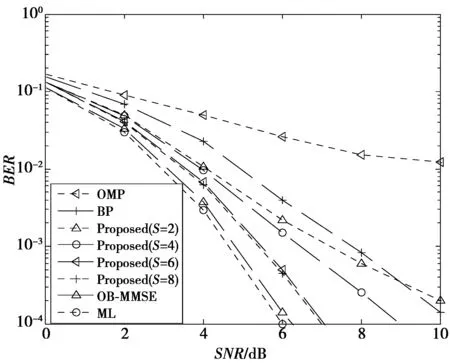
图3 QSM系统BER性能比较图 (Nt=64)Fig.3 BER performance comparison of QSM system(Nt=64)

仿真结果表明，在相同的频谱效率下，传统OMP算法误码性能较差，且在SNR≥8 dB时出现地板趋势。本文提出的算法随着每次迭代选择的天线索引个数S的增加误码性能显著提高。从仿真结果可以看出，索引个数S=6时，本文提出的算法的性能已达到最佳，性能曲线与OB-MMSE算法和ML算法相差较小。

综上，当每次迭代选择的天线索引个数S=6时，包含最优解的可能性与S=8相同，但比S=4，S=2包含最优解的可能性大，所以S=6的误码性能曲线与S=8时的误码性能曲线重合，优于S=4，S=2时的误码性能曲线。虽然随着天线索引个数S的增加误码性能显著提高，但随之增加的计算复杂度仍然远低于其它检测算法及ML算法。

3.2 计算复杂度分析

本文将每一次实值加法和实值乘法都定义为一次浮点运算，假设有A∈m×n，B∈n×p，C∈n×1，D∈n×1则AB，‖分别需要2mnp-mp，2n-1，n次浮点运算。根据(5)式，ML算法的计算复杂度为

(10)

本文提出的算法复杂度分析如表3所示。

表3 本文提出的算法计算复杂度分析

本文提出的算法计算复杂度与ML算法进行比较如表4所示，其中R=(C本文提出/CML)×100%为复杂度百分比，即本文提出算法的计算复杂度与ML算法的计算复杂度百分比：

从表3和表4可以看出，对于仿真参数Nt=32，Nr=16，采用4QAM调制方式的QSM系统，本文提出的检测算法在S=6时性能最佳，此时计算复杂度约为ML的4.7%；对于仿真参数Nt=64，Nr=16，采用4QAM调制方式的QSM系统，计算复杂度约为ML的1.3%。虽然OMP算法的计算复杂度最低，但是其误码性能却最差。可见，本文提出算法的计算复杂度相较于ML所占的复杂度百分比，随着发射天线的增加而降低。

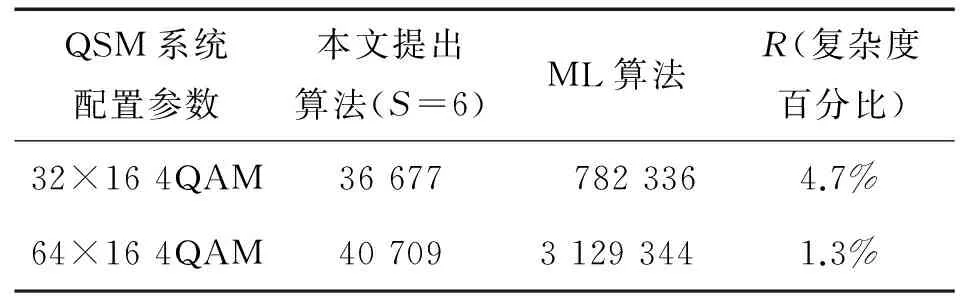
表4 本文提出算法与ML算法计算复杂度比较

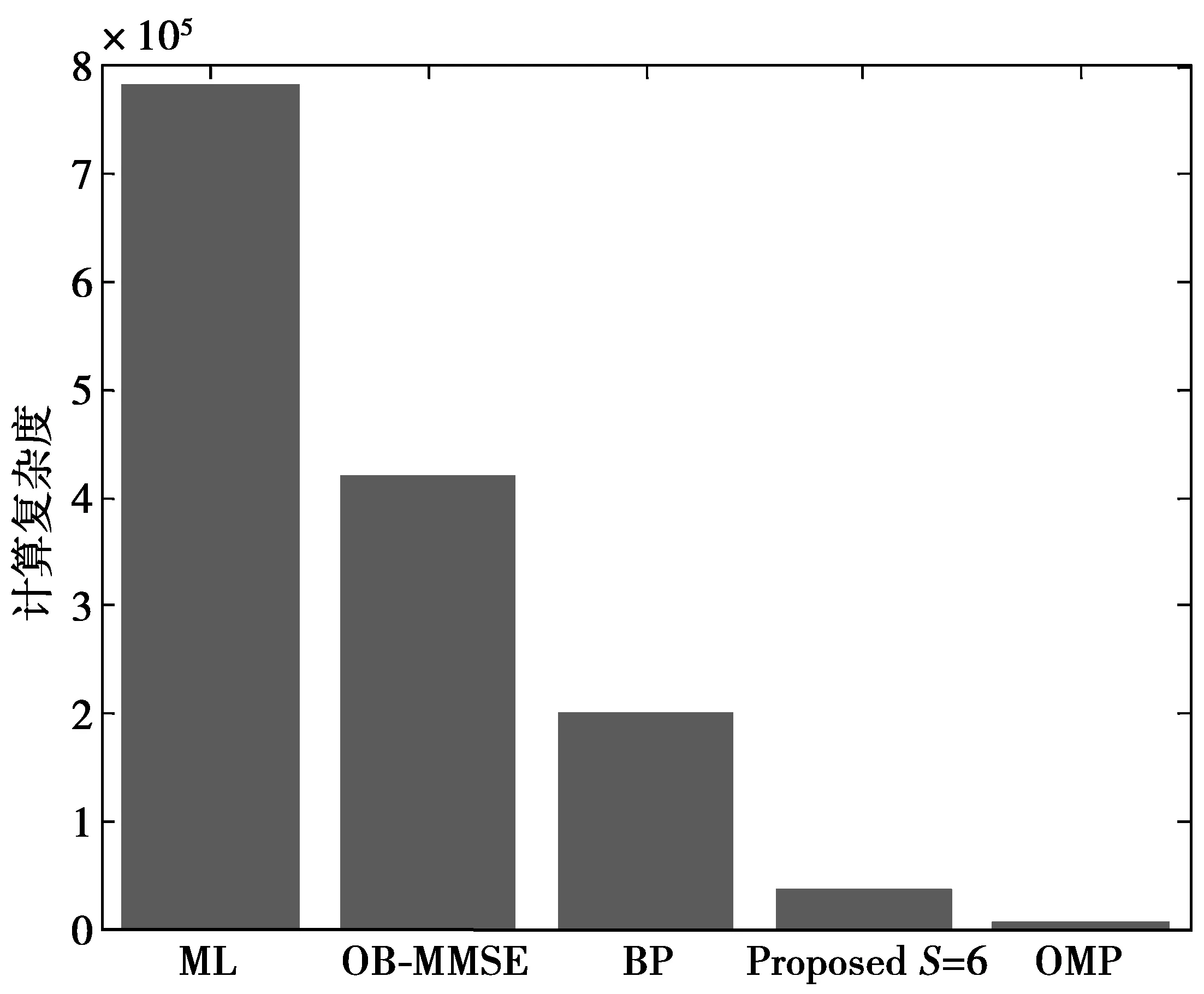
图4 QSM系统计算复杂度(Nt=32)Fig.4 Computation complexity of QSM system(Nt=32)

4 总 结

在正交空间调制(QSM)系统中，为避免ML最优检测算法因联合检测符号和天线而具有高计算复杂度导致不利用实际中实现的问题，将压缩感知理论应用在QSM系统接收端恢复出原始信号。本文根据QSM系统生成发送向量的特点，分析OMP算法为代表的贪婪算法，同时利用最大似然的思想得到一种新的次优检测算法。仿真结果表明，提出的次优检测算法能够在计算复杂度和误码性能之间进行平衡，有着较低的复杂度和较优的误码性能。此外，绿色通信逐渐成为未来通信发展趋势，这也限制了类似ML、OB-MMSE这类高复杂度检测算法的实际应用范围。随着大规模天线阵列MIMO的研究及发展，本文提出的检测算法具有一定的实际意义和较高的工程应用价值。

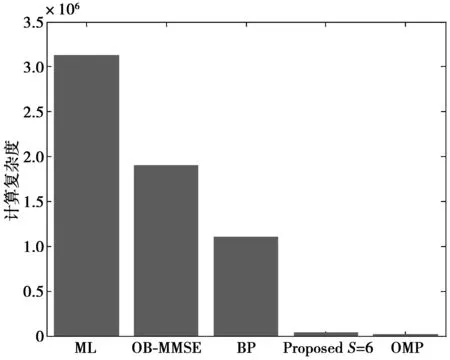
图5 QSM系统计算复杂度(Nt=64)Fig.5 Computation complexity of QSM system(Nt=64)

[1] MAO Guoqiang.5G Green Mobile Communication Networks[J].China Communications,2017,14(2):183-184.

[2] RAED Y M, HARALD H, SINAN S，et al. Spatial modulation[J]. IEEE Transactions on Vehicular Technology, 2008, 57(4): 2228-2241.

[3] MIETZNER J, SCHOBER R, LAMPE L, et al. Multiple-antenna techniques for wireless communications-A comprehensive literature survey[J]. IEEE Commun Surv Tut, 2009, 11(2): 87-105.

[4] CHAU Y, YU Shihong. Space modulation on wireless fading channels[C]//Vehicular Technology Conference.[S.l.] :IEEE,2001: 1668-1671.

[5] SONG S, YANG Y L, XIONG Q,et al. A channel hopping technique I: Theoretical studies on band efficiency and capacity[C]//Communications, Circuits and Systems, 2004. International Conference on.[S.l.]:IEEE,2004: 229-233.

[6] FU J, HOU C, XIANG W, et al. Generalised spatial modulation with multiple active transmit antennas[C]// GLOBECOM Workshops.[S.l.]:IEEE, 2010:839-844.

[7] MESLEH R, IKKI S S, AGGOUNE H M. Quadrature Spatial Modulation[J]. IEEE Transactions on Vehicular Technology, 2014, 64(6):1-1.

[8] BASAR E, YIGIT Z. Low-Complexity Detection of Quadrature Spatial Modulation[J]. Electronics Letters, 2016, 52(20): 1729-1731.

[9] LI J, JIANG X, YAN Y, et al. Low Complexity Detection for Quadrature Spatial Modulation Systems[J]. Wireless Personal Communications, 2017(4): 1-13.

[10] DUARTE M F, ELDAR Y C. Structured Compressed Sensing: From Theory to Applications[J]. IEEE Transactions on Signal Processing, 2011, 59(9):4053-4085.

[11] YU C M, HSIEH S H, LIANG H W, et al. Compressed Sensing Detector Design for Space Shift Keying in MIMO Systems[J]. IEEE Communications Letters, 2012, 16(10):1556-1559.

[12] LIU W, WANG N, JIN M, et al. Denoising Detection for the Generalized Spatial Modulation System Using Sparse Property[J]. IEEE Communications Letters, 2014, 18(1):22-25.

[13] GARCIA R A, MASOUROS C. Low-Complexity Compressive Sensing Detection for Spatial Modulation in Large-Scale Multiple Access Channels[J]. IEEE Transactions on Communications, 2015, 63(7):2565-2579.

[14] XIAO Y, YANG Z, DAN L, et al. Low-Complexity Signal Detection for Generalized Spatial Modulation[J]. Communications Letters IEEE, 2014, 18(3):403-406.

[15] CHEN C E, LI C H, HUANG Y H. An Improved Ordered-Block MMSE Detector for Generalized Spatial Modulation[J]. IEEE Communications Letters, 2015, 19(5):707-710.

(编辑：张 诚)

Alowcomplexitysignaldetectorinquadraturespatialmodulationsystem

CHEN Fatang, LIU Yan, LI Yuhe

(Chongqing Key Lab of Mobile Communications, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R. China)

QSM (quadrature spatial modulation) has been paid much attention recently to an extended spatial modulation transmission scheme which improves the spectral efficiency by independently transmitting the real and imaginary parts of a complex data symbol. ML (maximum likelihood) detector for QSM system has to exhaustively search in the whole search space, so the complexity of ML detector is very high. For the high complexity of QSM system detection, a low complexity detector based on the concept of CS (compressed sensing) is proposed by exploiting the fixed sparse property of quadrature spatial modulation system signals. The simulation results show that the novel detector exhibits near-maximum likelihood detector bit error performance and its complexity is about 4.7% of ML.

quadrature spatial modulation (QSM); detector; low complexity; compressed sensing (CS)

s：The National Science and Technology Project of China(2017ZX03001021-004); The Science and Technology Project of Chongqing Municipal Education Commission(KJ1500428); The Fundamental and Frontier Research Project of Chongqing(cstc2016jcyjA0209)

TN929.5

A

1673-825X(2017)05-0604-07

陈发堂(1965-)，男，重庆綦江人，研究员，硕士生导师，主要研究方向为移动通信和TD-LTE系统开发。E-mail:Chenft@cqupt.edu.cn。

刘 燕(1993-)，女，安徽合肥人，硕士研究生，主要研究方向为LTE-A系统物理层算法和空间调制技术。E-mail:790693383@qq.com。

李玉河(1992-)，男，四川巴中人，硕士研究生，主要研究方向为LTE-A系统物理层算法及DSP实现和空间调制技术。E-mail:759202752@qq.com。

2017-04-12

2017-10-28

刘 燕 790693383@qq.com

国家科技重大专项(2017ZX03001021-004)；重庆市教委科学技术研究项目(KJ1500428)；重庆市基础与前沿研究计划项目(cstc2016jcyjA0209)

10.3979/j.issn.1673-825X.2017.05.005