降低FBMC-OQAM峰均值比方法的研究

李若梦，唐青青

(重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065)

降低FBMC-OQAM峰均值比方法的研究

李若梦，唐青青

(重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065)

针对滤波器组多载波/正交幅度调制(filter bank multi-carrier/offset quadrature amplitude modulation，FBMC-OQAM)系统峰均值比(peak to average power ratio,PAPR)过高的问题，提出一种应用在FBMC-OQAM系统中的双层迭代部分传输算法。所提算法在传统迭代部分传输序列(iterative partial transmit sequence algorithm，IPTS)算法的基础上，改进搜索方式，将相位因子向量分为奇偶分别进行迭代，扩大了搜索范围。再结合FBMC-OQAM系统的重叠特性，对数据块之间的重叠部分加以利用，将使得当前符号块加权后的信号与寄存窗中的信号之和的PAPR最小的相位因子向量作为最优相位因子向量，从而在不增加过多计算量的基础上提高了抑制PAPR的性能。仿真结果表示，改进的双层迭代部分传输序列(partial transmit sequence algorithm，PTS)算法的PAPR抑制效果显著优于传统算法，误码率低于传统算法，且计算复杂度显著低于PTS算法。

滤波器组多载波；峰均值比；迭代PTS算法

0 引 言

近年来，多载波技术(filter bank multi-carrier, FBMC)被广泛应用于高速率数据传输的通信系统，并被认为是未来无线通信的候选调制方案。其中，正交频分复用(orthogonal frequency division multiplexing, OFDM)技术是最为著名的多载波方案之一，然而循环前缀(cyclic prefix, CP)降低了系统的频谱效率，并且矩形脉冲整形导致了十分严重的高带外辐射。为了消除这些影响，滤波器组多载波-偏移正交幅度调制(filter bank multi-carrier /offset quadrature amplitude modulation, FBMC-OQAM)越来越受到研究者的关注[1-3]，作为第5代无线通信网络的候选调制方案，FBMC/OQAM通过基于快速傅立叶逆变换/快速傅里叶变换(inverse fast Fourier transform/fast Fourier transform, IFFT/FFT)的滤波器组和OQAM符号将实数符号以FBMC/QAM符号速率的2倍载入子载波。因此，在理论上FBMC/OQAM具有较高的频谱效率以及频偏和多普勒扩展的鲁棒性。此外，FBMC/OQAM系统不需要循环前缀，却可以提供比CP-OFDM系统更高的数据速率。然而，所有多载波通信系统都存在高峰均值比(peak to average power ratio, PAPR)的问题，FBMC-OQAM也不例外。

通常，高PAPR意味着需要使用具有巨大输入回退的线性放大器。因此，为了解决高PAPR的问题，同时又不影响功率效率，已经有了许多降低PAPR的方案。在OFDM系统中，降低PAPR的方案已经相当成熟，而且具有可忽略的误码率(bit error ratio, BER)降级[4]，文献[5-7]对不同抑制OFDM系统PAPR的方案进行了概述，但由于FBMC系统固有的符号重叠，现在降低FBMC-OQAM系统PAPR的方法还比较少，用于FBMC系统中的技术通常都需要额外的处理和复杂性来解决问题[8-10]。目前，降低FBMC-OQAM的方案基本有2种思路：①直接把OFDM系统降低PAPR的方法应用在FBMC中[11]；②根据FBMC-OQAM系统的特点，提出新的算法[12]。例如文献[11]对选择性映射(selected mapping, SLM)算法进行改进，提出多数据块联合优化的SLM(multi-block selective mapping, MB-SLM)算法，文献[12]提出了具有多块联合优化的PTS(multi-block PTS, MB-PTS)方案，证明了当重叠性质被合理利用时，FBMC的表现优异于OFDM。

本文分析了FBMC-OQAM系统中的PAPR和目前已有的抑制方法，通过对传统算法进行改进，提出一种应用在FBMC-OQAM系统的基于迭代部分传输序列(iterative partial transmit sequences,IPTS)算法的改进双层IPTS算法，结合FBMC-OQAM数据块重叠的系统特性，再引入双层思想，在每层搜索中，将相位因子向量按照迭代次序分成奇偶向量分别进行迭代，对数据块之间重叠的部分加以利用，完成内层搜索，再进行外层搜索，形成新的双层IPTS算法。该算法能够显著降低系统的PAPR，且具有较低的计算复杂度。

1 FBMC-OQAM系统模型

1.1 系统模型

FBMC-OQAM的信号发送图如图1所示。信号首先经过QAM调制，映射成为信号Am，其中，Am=[a0,m,a2,m,…,aN-1,m]，m代表符号块索引，N代表子载波数，经过串并转换后，信号的实部和虚部分开在子载波上传输，再经过原型滤波器和相位调制，子载波信号叠加得到传输的FBMC-OQAM数据块。

FBMC-OQAM系统中符号块的数学描述为

(1)

(1)式中：R和I代表信号的实部和虚部；h(t)表示长度为βT的原型滤波器；β为重叠系数；n表示子载波索引。h(t)在时间和频率上的移动得到的hm,n(t)表示为

hm,n(t)=h(t-mτ0)ej(m+n)π/2ej2πnv0t

(2)

(2)式中：mτ0表示函数在时间上的偏移，以半个周期为步长；nv0表示函数在频率上的偏移，以相邻子载波的频差为步长；相位因子ej(m+n)π/2的作用是保证同相与正交分量之间的错位。

FBMC-OQAM系统中，第m个数据块的时域表达式为

(3)

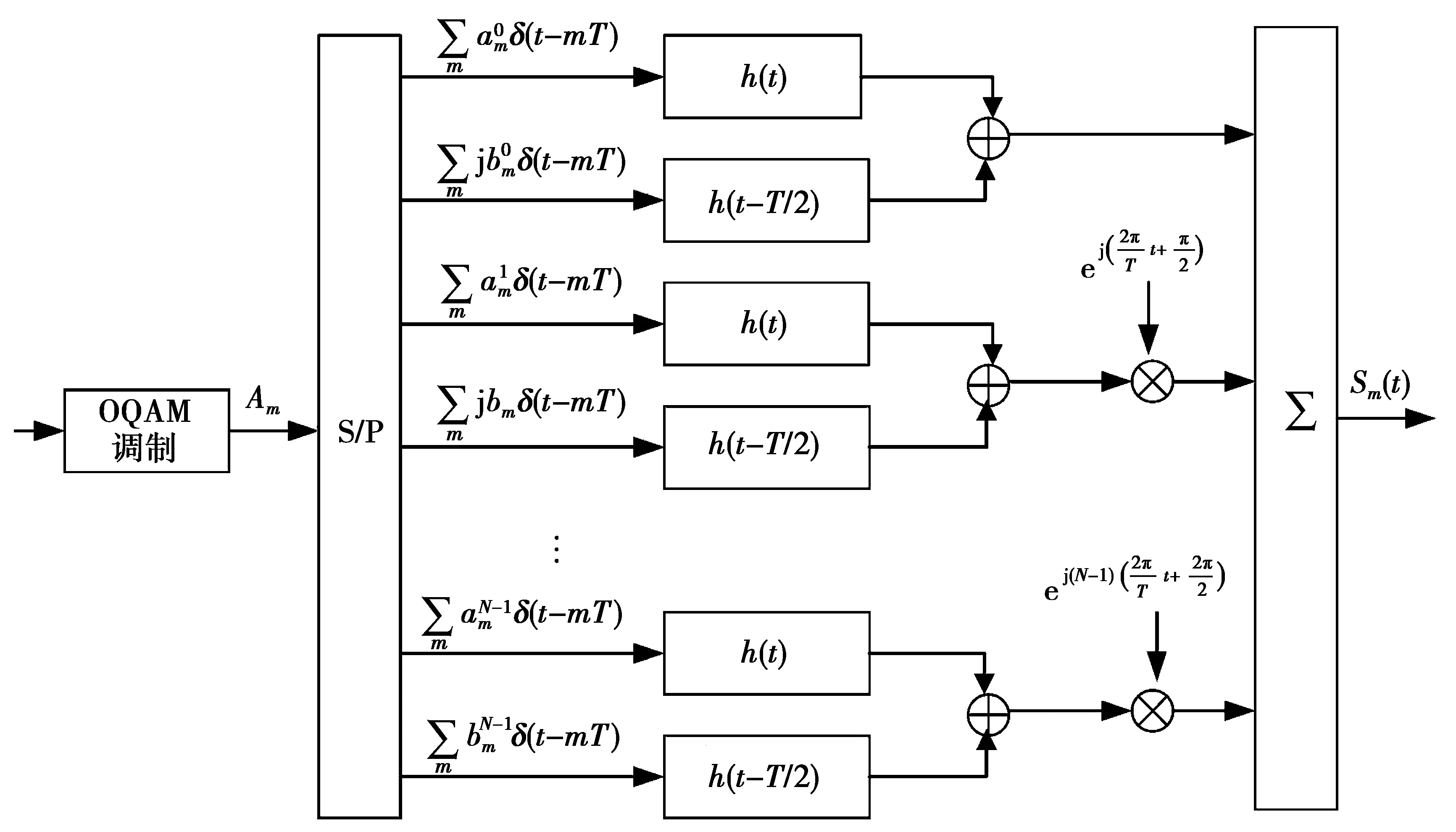
图1 FBMC-OQAM系统框图Fig.1 Block diagram of FBMC-OQAM system

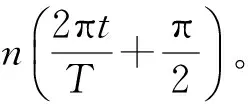
经过QAM调制后的数据可以表示为

(4)

(3)式可表示为

(5)

(5)式中表示的数据块示意图如图2所示。可以看出，每个sm(t)0≤m≤(M-1)由2部分组成，且2部分交错T/2个周期。每个数据块的长度为βT，第m个数据块sm(t)的长度为(β+1/2)T，则M个数据块的长度为(β+M+1/2)T。

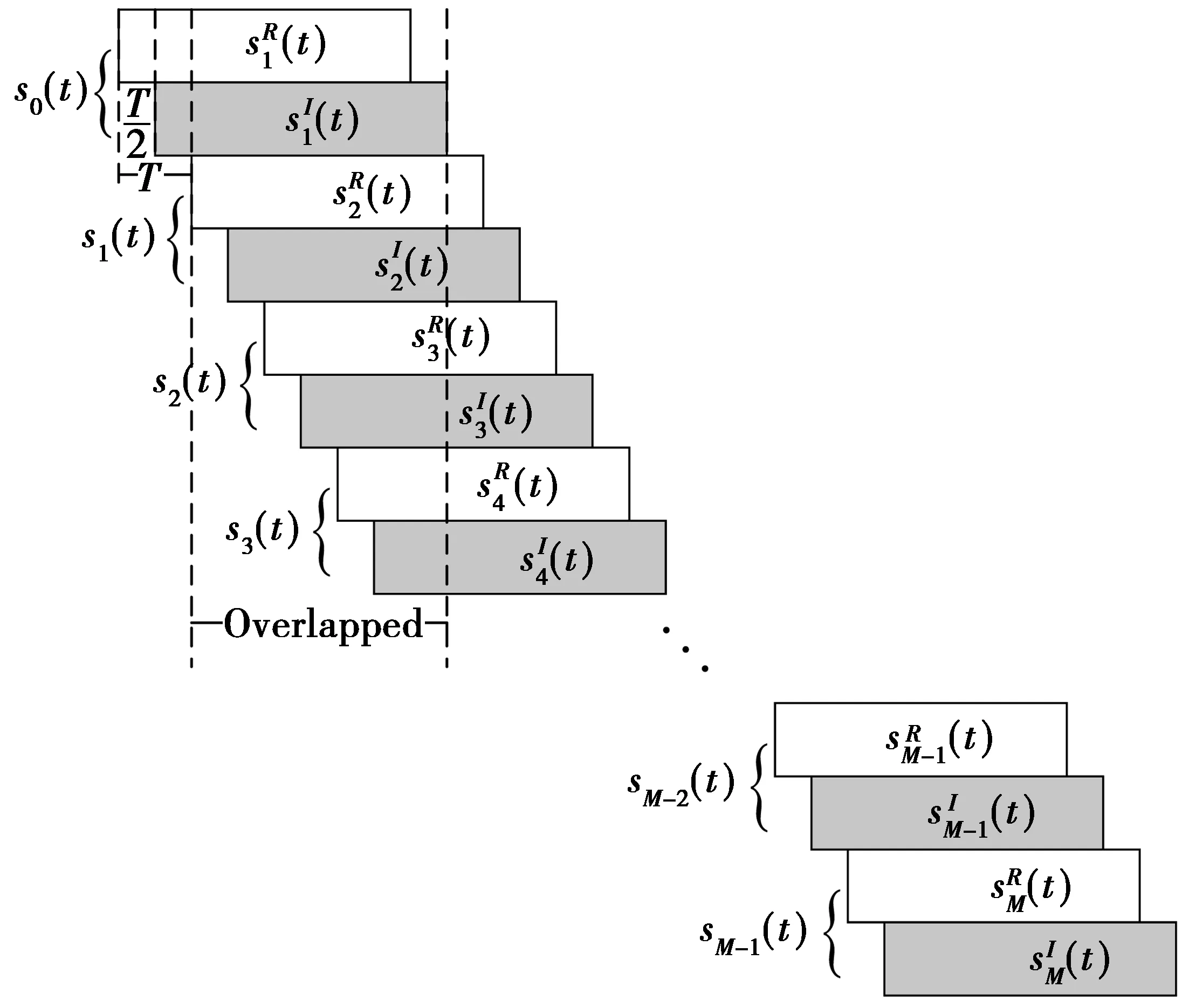
图2 FBMC-OQAM信号结构图Fig.2 Structure of FBMC/OQAM signal

在这里，我们采用PHYDYAS滤波器[13]作为原型滤波器，涉及的分析参数有子载波数量N，重叠因子β，滚降系数α和滤波器长度L=βN。β=4时，原型滤波器的时域脉冲响应与滤波器系数表示为

(6)

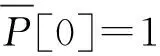
1.2 系统PAPR分析

在PAPR中，用于描述信号s(t)的参量被定义为

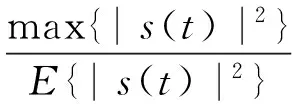
(7)

(7)式中：|s(t)|是信号的幅度值；E{·}为信号的期望值。

通常，用补充累计分布函数(complementary cumulative distribution function,CCDF)来表示γ，它可以计算出PAPR超过给出的门限值P0的概率。在OFDM中，γ仅仅是测量单个数据块的PAPR的函数，而在FBMC-OQAM中，γ是几个连续数据块的函数，这种依赖性需要考虑FBMC-OQAM信号模型再进一步调查。

考虑到FBMC-OQAM的重叠性与信号在FBMC系统中的瞬态，为了尽可能准确地测量FBMC中的PAPR，可以将信号s(t)分成Q+α个时间间隔，每段长度都为T(最后一段长为T/2)。每段时间间隔的PAPR可以定义为

i=0,1,…,M+β-1

(8)

目前，抑制PAPR有很多方法，部分传输序列(partial transmit sequences,PTS)[14-16]作为一种无失真方法，应用最为广泛。

2 传统解决方案

PTS的思想是将输入的频域信号分割成V个互不重叠的子块，所有子块乘以不同的相位旋转因子，并分别计算不同组合的PAPR，最后在所有组合中选择PAPR最小的一组发送。算法的实现如图3所示。

假设N个子载波组成的输入信号为X=[X0,X1,…,XN-1]，经过分割的V个子块可以表示为

(9)

(9)式中，v代表子块索引。本文采用相邻分割，将分割后的V个子块分别与相位旋转因子相乘，得到

(10)

(10)式中，bv∈{ej2πi/W,i=0,1,…,W-1}，W表示子块中的相位因子的个数。

对加权后的子序列进行傅里叶逆变换，使信号由频域转为时域，表示为

(11)

PTS算法的目标是选择可减小X′峰均比的一组相位因子，即最优相位因子。即

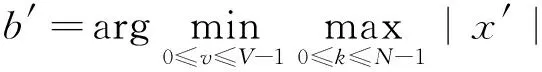
(12)

可以看出，PTS算法在执行的时候需要遍历所有组合的PAPR，计算复杂度太大。因此，有学者提出了演进的部分传输序列算法，例如IPTS算法，双层相位部分传输序列方法(dual layered phase sequencing, D-IPTS)，这些方法都是以牺牲PAPR性能为代来换取复杂度的降低。

IPTS[17]的步骤：选择{±1}为候选相位因子，将数据分成V块再进行IFFT变换之后，开始迭代步骤。

步骤1将V个子序列块的相位因子均设为1，计算其PAPR值；

步骤2将第1个相位因子变成-1，并计算其PAPR值，若新的PAPR值小于原来的PAPR，就将第1个相位因子保留为-1，否则为1；

步骤3依次对第2，第3，直到第V个相位因子进行变换，即得到最终的相位因子向量。

该算法的优点是复杂度低，但性能不如PTS算法，因为在搜索相位因子时，不能寻求全局最优的相位因子组合。因此，出现了DIPTS算法，该算法的基本思想是采用两层相位因子优化数据，对数据进行2次优化。

具体思想：将N个子载波的数据块分成V个子序列，再将V个子序列划分为D个区段，则每个区段包含V/D个子序列。即相位优化分为2层：微观层优化和宏观层优化。第1层，即微观层，数据被分成V个子序列，在每个子序列内采用IPTS算法进行优化，保留得到的最小PAPR的一组相位因子。 第2层，采用宏观优化，将V个子序列分成D个区段，将每个区段看作一个整体，对D个区段进行IPTS优化。双层结构的模型如图4所示。

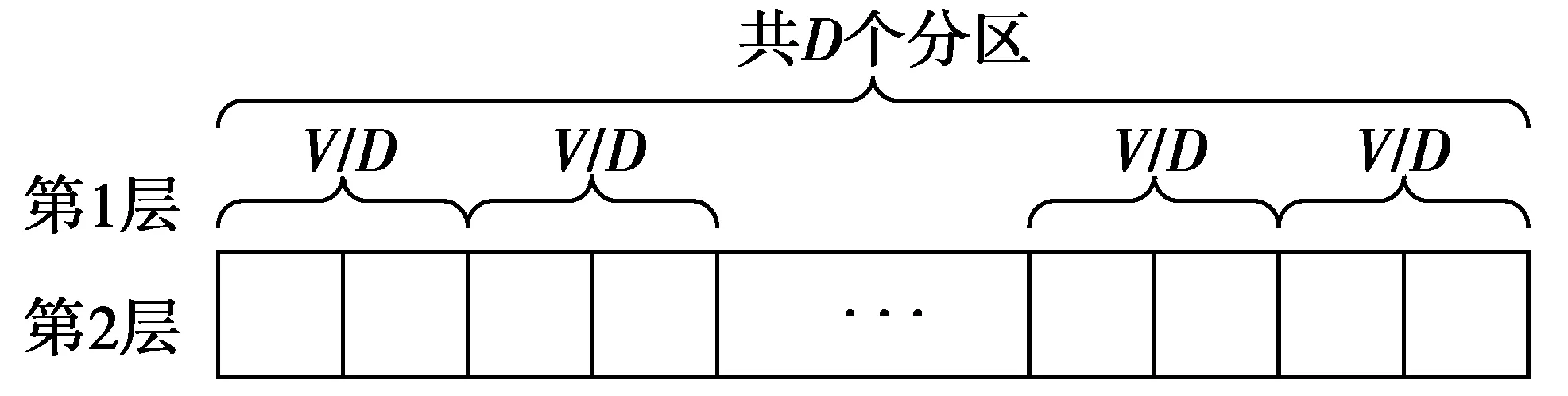
图4 双层搜索算法分块示意图Fig.4 Structure of the algorithm with dual layered phase

本文只针对自下而上算法进行研究与优化，数据信号被划分为VvDd的形式，M个数据符号被划分为V个子数据序列，D个区段，每个区段将V/D个相位旋转因子看作一个整体，对子序列进行优化。

3 改进算法

所提算法在IPTS算法的基础上加以改进，具体内容如下。

用于OFDM降低PAPR的方法都是针对单独的数据块，而FBMC-OQAM系统因为原型滤波器使用非矩形脉冲，且传输信号的实部虚部相差半个符号周期，导致FBMC系统数据块之间相互重叠，因此，为了有效降低FBMC-OQAM系统的PAPR，需要考虑相邻数据块所产生的影响，对IPTS算法加以改进。

即增添一个寄存窗口以保存即将与当前符号进行混叠的信号，对每个符号块进行调制时，将之前的符号块的最优传输序列寄存在寄存窗。进行调制时，保留使得当前符号块加权后的信号与寄存窗中的信号之和的PAPR最小的相位因子向量为作为最优相位因子向量。

首先，把FBMC-OQAM信号s0(t)=[s0,0(t),s0,1(t),…,s0,N-1(t)]，分割成V个子块，分割之后的信号表示为

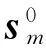
(13)

(13)式中，V表示子数据块的个数。每一个子数据块可以表示为

(14)

(13)式中的每一个子数据块的信号可以表示为

0≤n≤N-1,0≤v≤V-1

(15)

第1个数据块的相位因子向量的合集表示为

(16)

(17)

因为数据块间存在重叠，所以计算第2个数据块的最佳相位因子向量时，需要考虑之前数据块的影响。假设数据块与最佳相位因子向量相乘后得到的最优传输序列表示为

(18)

因此，第2个的最佳相位因子集合可以通过(19)式得到

(19)

按照(19)式，在搜索每个子数据块时都要考虑前一个重叠数据块的影响，直至第M个数据块。

第m个FBMC-OQAM数据块的相位因子集合可以表示为

(20)

所有数据块的相位因子向量确定之后，可以得到最佳相位因子向量为

c={c0,c1,…,cM-1}

(21)

最优传输序列为

(22)

然后，对IPTS搜索相位因子的迭代方式进行改进，把将要进行变换的第i个相位因子向量bi，按照i分为奇偶2类，若i为偶数，将bi-2的第i/2个因子变为-1；若i为奇数，将向量bi-2的第(i+1)/2个因子变为-1，再与因子改变之前的PAPR进行比较，保存PAPR较低的相位因子向量。

最终，保留的相位因子向量即为数据块的最优相位因子向量。变换几次后就可以发现，每次迭代时搜索的相位因子向量的数量都比传统的IPTS算法扩大了2倍，所有可能的相位因子的组合都能被搜索到。

假设有N个子载波，每个子载波有M个数据符号块，将每个数据符号分成V个子序列块，V个子序列块再分成D个分段。改进算法的具体步骤如下。

步骤1搜索内层相位因子，设置初始相位因子向量为1，即b=[1,1,…,1]；

步骤2从第1段开始搜索，将相位因子全部设置为1，记此时的相位因子向量为b0和b1，计算此时信号的PAPR值，记为PAPR0；

步骤3将即将得到的向量b的序列数记为i，i≥2，将i分为奇偶2类，开始依次按照序号进行迭代；

步骤4当i为偶数时，将向量bi-2的第i/2个因子变为-1，得到的相位因子向量记为bi，计算此时信号的PAPR，并与PAPR0进行比较，若小于PAPR0,则赋给PAPR0，例如当i=4时，将向量b2的第2个因子变为-1，记得到的相位因子为b4，再计算信号的PAPR，并与PAPR0比较；

步骤5当i为奇数时，将向量bi-2的第(i+1)/2个因子变为-1，得到的相位因子向量记为bi，计算此时信号的PAPR，并与PAPR0进行比较，若小于PAPR0,则赋给PAPR0，例如当i=5时，将向量b3的第3个因子变为-1，记得到的相位因子向量为b5，再计算信号的PAPR，与PAPR0比较；

步骤6直到第1个区段的所有2V/D个相位因子都被搜索到为止，迭代结束，即完成第1个区段的搜索；

步骤7以同样的方式搜索第2个区段的相位因子向量，同时将第1区段所得到的最小PAPR的相位因子向量保留下来，未优化的仍然记为1。直到所有区段都搜索完毕，就得到了内层的最佳相位因子向量。将此时的最佳相位因子向量记为c0，相应的最佳候选序列为s0(t)c0；

步骤8计算第2个数据块s1(t)的最佳相位因子向量。分成数据子块后依然根据改进的IPTS算法进行搜索，得到i个相位因子向量，数据子块经过相位因子加权得到多个候选序列。由于数据块s1(t)与s0(t)重叠，因此，求其最优传输序列时需要考虑s0(t)传输序列的影响，此时候选序列中与s0(t)c0相加的PAPR最小的bi即为最优传输序列，记得到的最佳相位因子向量为c1，最优传输序为s1(t)c1；

步骤9以此为例，计算出所有数据块的内层最佳相位因子向量为C1={c1,0,c1,1,…,c1,M-1}；

步骤10接下来搜索外层相位因子向量，将所有外层向量因子均设置为1；

步骤11将V组分为D区之后，每个区段的相位因子向量含有V/D个向量因子，把每个区段内的向量因子看作一个整体，变换时，令每一区段的bi全部等于1或-1；

步骤12按照内层的搜索方法搜索外层相位因子，依次计算M个数据块的最佳相位因子向量c2,m，得到最优传输序列sm(t)c2,m；

步骤13由此得到M个数据块的外层最佳相位因子向量为C2={c2,0,c2,1,…,c2,M-1}；

步骤14将得到的内层相位因子与外层相位因子对应位置相乘，即为最后所需的最佳相位因子向量。

改进算法在选择每个数据块的最佳相位因子向量时，不仅扩大了搜索范围，引入双层结构，还考虑了数据块之间的重叠产生的影响，因此，可以预见与每个数据块直接应用传统方法相比，改进算法能够更好地抑制系统的PAPR。

接下来对改进算法的复杂度进行分析，对于有M个数据块的FBMC-OQAM系统，这里的复杂度指的是每发送1个FBMC符号需要计算的PAPR次数，其中，内层相位因子需要D×2V/D次迭代，因为每个分区需要2V/D次迭代，共有D个分段，而外层因子的确定需要2D-1次迭代，即可得到M个数据块的搜索复杂度。每个数据块被分为V个子数据块，每个子数据块有W个相位旋转矢量。各算法复杂度的比较如表1所示，可以看出，与PTS算法相比，改进算法不仅在复杂度上较低，性能也更优。虽然复杂度和DIPTS相同，较IPTS有所增加，但PAPR的抑制性能明显优于2种算法，因此，与IPTS算法相比，改进算法以较小的复杂度增加换取较大的性能改善，降低了系统成本。这些方法降低PAPR的性能比较将在第4节中说明。

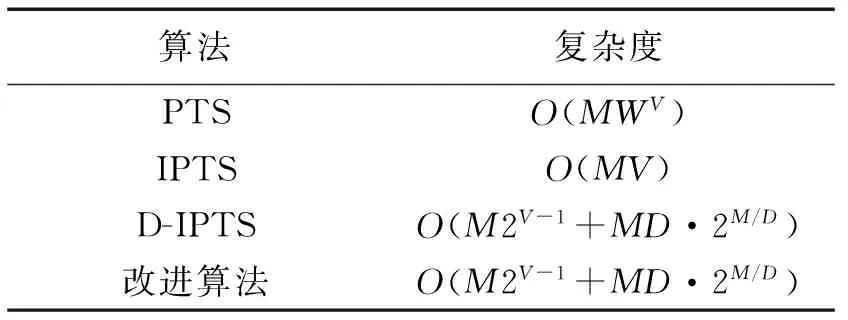
表1 各算法复杂度的比较

4 仿真结果分析

在本节中，对改进算法与传统抑制PAPR算法的性能进行对比分析。仿真参数：数据块个数M=250，子载波数N=32，采用4QAM调制方式，重叠因子β设为4。

FBMC-OQAM系统中应用传统PTS，IPTS，DIPTS方法的效果对比如图5所示。分组数V设定为8，可以看出，当CCDF=0.000 1时，IPTS，DIPTS，PTS使系统的PAPR性能分别提高了1.99 dB，2.51 dB，3.52 dB。可见，IPTS算法性能较PTS算法有较大差距，DIPTS虽然在IPTS的基础上提高了性能，但性能还是不如PTS算法，所以还需要对FBMC-OQAM系统抑制算法进一步研究。

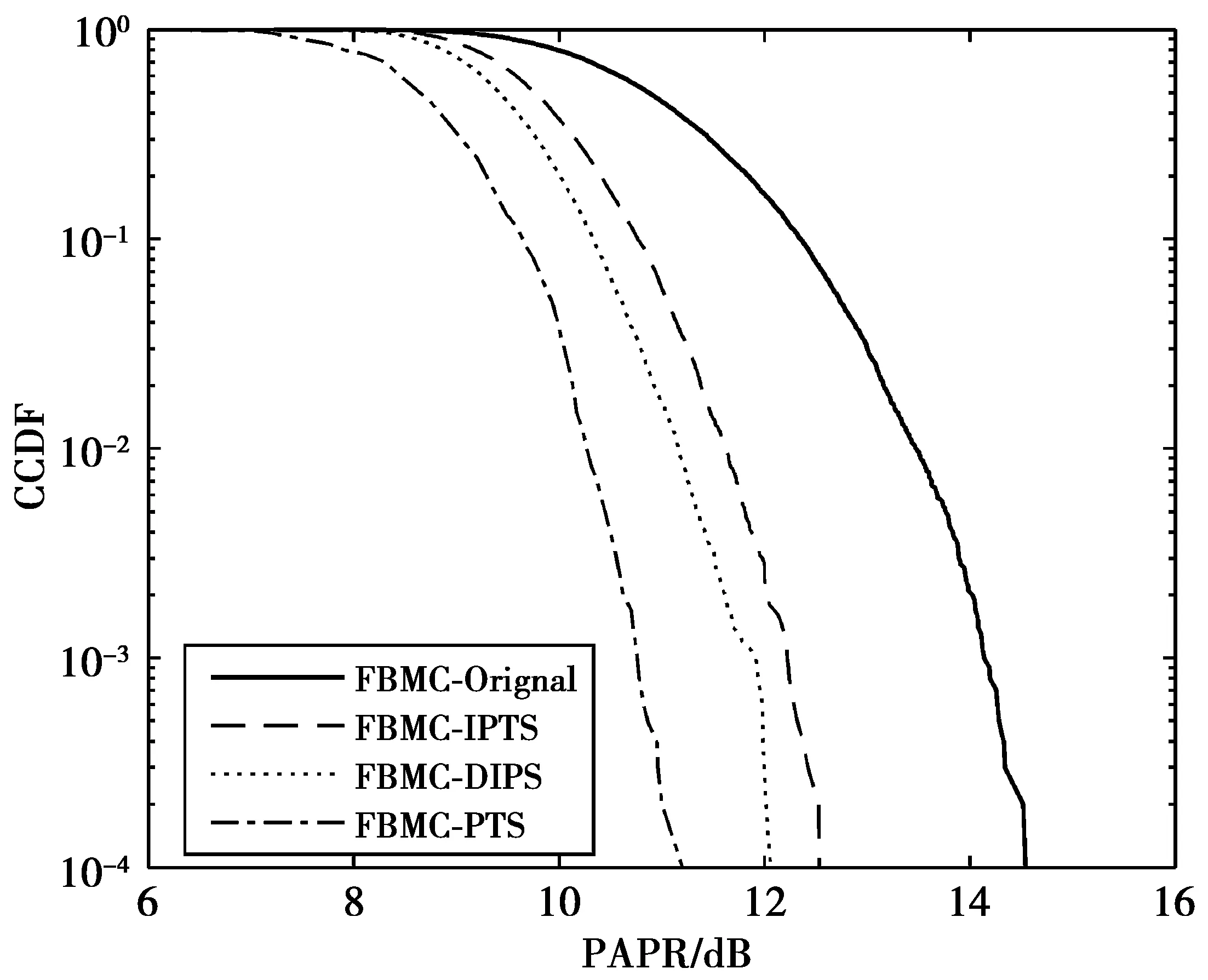
图5 传统算法的抑制效果图Fig.5 PAPR reduction of the conventional schemes

改进算法与传统PTS，DIPTS算法的性能对比如图6所示。分组数V=8，当CCDF=0.000 1时，PTS，DIPTS，改进算法的PAPR性能分别提高了约2.46 dB，3.12 dB，3.9 dB，可见，改进后的算法对系统PAPR的抑制性能是最好的，这是因为引入了双层思想的改进方法应用在FBMC-OQAM系统中更加合理，所以取得的效果更好。

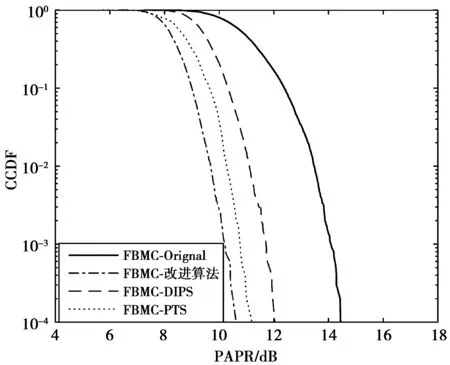
图6 改进方法与传统方法抑制PAPR对比图Fig.6 PAPR reduction of the conventional scheme and improved scheme

改进方法和DIPTS方法的PAPR性能对比如图7所示。当分组数V=4，V=8，CCDF=0.000 1时，改进算法降低系统PAPR的效果比传统DIPTS算法提高了1.62 dB和1.7 dB，可以看出，分组数不同时，所提的算法效果依然明显优于传统DIPTS方法。

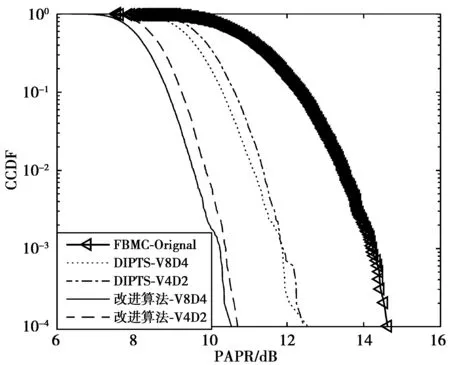
图7 当V，D取值不同时改进算法与传统算法的抑制PAPR对比图Fig.7 PAPR reduction of the conventional scheme and improved scheme When V，D values are different

图8给出了所提算法中，V，D取不同值时的PAPR抑制性能对比。CCDF=0.000 1的情况下，当V=4，D=2时，系统抑制PAPR的性能最差，其次，是V=8，D=4。当V=16，D=8时，系统的性能最优，相比于V=16，D=4时，性能提高了0.339 dB。由分析可知，算法性能的主要影响因素是V和D，当D一定时，V越大，系统的复杂度越高，PAPR性越好；同样地，当V一定时，D越大，系统的复杂度越大，性能也越好。

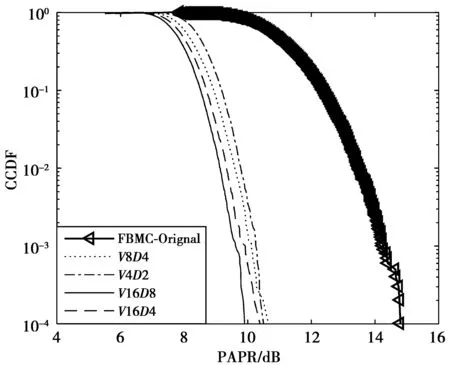
图8 当V，D取值不同时改进算法抑制PAPR对比图Fig.8 PAPR reduction of the conventional scheme and improved scheme when V，D values are different

各种算法在加性高斯白噪声(additive white gaussian noise，AWGN)信道中的误码率(bit error ratio，BER)性能对比如图9所示。分组数V=8，信道采用高斯白噪声信道，信号放大器输出功率等于FBMC-OQAM信号的平均功率放大器的输出功率，通过分析能够发现，IPTS与DIPTS算法的误码率基本相同，PTS算法则优于这2种算法，这是因为PTS算法处理PAPR的性能优于后者，而改进算法的误码率较PTS算法有了较小的提升，可见，考虑信号重叠特性的合理性，改进算法的PAPR抑制能力更强，处理后的信号出现高峰值的几率更低，所以具有更好的BER性能。

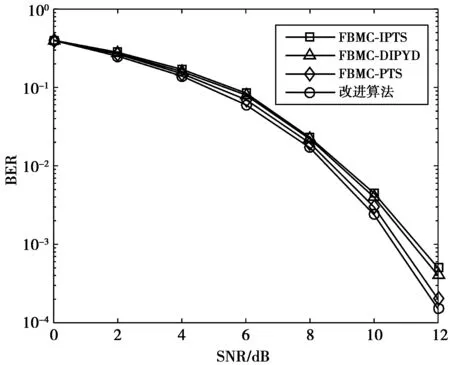
图9 各种算法在AWGN信道中的BER性能对比Fig.9 Comparison of BER performance of various algorithms in AWGN channel

5 结束语

迭代PTS方法是抑制PAPR的经典方法，但应用在FBMC-OQAM系统中还有着诸多不足，本文考虑到FBMC-OQAM的系统结构特点，对迭代PTS算法加以改进，结合系统的重叠特性，扩大算法的搜索范围，同时引入双层思想，从而能够有效地降低系统的PAPR，并且未显著增加复杂度。通过仿真验证了改进的算法在FBMC-OQAM系统中的可行性和有效性。结果证明，应用改进算法后，系统的PAPR得到了明显的抑制。

[1] PETROV D, OBORINA A, GIUPPONI L, et al.Link performance model for filter bank based multicarrier systems[J].Eurasip Journal on Advances in Signal Processing, 2014, 2014(1):169.

[2] YOUSSEF R, CAISSIERE M, HELARD M, et al. Distributed coding/modulation scheme with OFDM/OQAM based transmission for wireless cooperative relays systems[C]//IEEE.International Symposium on Personal Indoor and Mobile Radio Communications.New York:IEEE Press, 2014:1196-1200.

[3] NADAL J, NOUR C A, BAGHDADI A. low-complexity pipelined architecture for FBMC/OQAM transmitter[J]. IEEE Transactions on Circuits & Systems II Express Briefs, 2016, 63(1):19-23.

[4] FARHANG B B.OFDM Versus Filter Bank Multicarrier[J].IEEE Signal Processing Magazine,2011,28(3):92-112.

[5] WALDHAUSER D S, NOSSEK J A. Multicarrier systems and filter banks[J].Advances in Radio Science, 2006,4(C1):165-169.

[6] MOGENSEN P, PAJUKOSKI K, TIIROLA E, et al. 5G small cell optimized radio design[C]//IEEE.GLOBECOM Workshops.New York:IEEE Press,2014:111-116.

[7] 庄陵,翁海涛,王光宇.一种基于预留子载波的CA-FBMC系统PAPR抑制算法[J].重庆邮电大学学报：自然科学版,2016,28(5):713-720.

ZHUANG Ling, WENG Haitao, WANG Guangyu. An effective method of reducing PAPR in FBMC system with carrier aggregation[J].Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition, 2016,28(5):713-720.

[8] THEIN C, SCHELLMANN M, PEISSIG J. Analysis of frequency domain frame detection and synchronization in OQAM-OFDM systems[J]. Eurasip Journal on Advances in Signal Processing, 2014, 2014(1):83.

[9] PENG C, SHI Z J, ZHU S J. An overview of peak-to-average power ratio reduction techniques for O-OFDM system[J].Journal of Anhui Vocational College of Electronics & Information Technology, 2014,2(5):54-62.

[10] MOHAMMADY S, SIDEK R M, VARAHRAM P, et al. A low complexity selected mapping scheme for peak to average power ratio reduction with digital predistortion in OFDM systems[J].International Journal of Communication Systems, 2013, 26(4):481-494.

[11] LAABIDI M, ZAYANI R, BOUALLEGUE R. A novel multi-block selective mapping scheme for PAPR reduction in FBMC/OQAM systems[C]//IEEE. Information Technology and Computer Applications Congress. New York: IEEE Press, 2016:1-5.

[12] QU D, LU S, JIANG T. Multi-block joint optimization for the peak-to-average power ratio reduction of FBMC-OQAM signals[J].IEEE Transactions on Signal Processing, 2013, 61(7):1605-1613.

[13] JIANG J Z,LING W K,OUYANG S.Efficient design of prototype filter for large scale filters bank-based multicarrier systems[J].IET Signal Processing,2017,1(5):521-526.

[14] YAO Y C, HUNG H L, WEN J H. OFDM system with reduce peak-to-average power ratio using optimum combination of partial transmit sequences[C]// International Conference in Swarm Intelligence. Berlin, Heidelberg：IEEE Press，2013:459-466.

[15] LEE K S, NO J S. Efficient PTS scheme with adaptive selection method for dominant samples in OFDM systems[C]//IEEE. Ubiquitous and Future Networks (ICUFN), 2017 Ninth International Conference on.New York:IEEE Press,2017: 387-392.

[16] HOU J, GE J, LI J.Peak-to-average power ratio reduction of OFDM signals using PTS scheme with low computational complexity[J].IEEE Transactions on Broadcasting, 2011, 57(1):143-148.

[17] CIMINI L J, SOLLENBERGER N R. Peak-to-average power ratio reduction of an OFDM signal using partial transmits sequences[J].IEEE Communications Letters, 2000, 4(3):86-88.

(编辑：王敏琦)

ResearchonthealgorithmforreducingPAPRofFBMC-OQAM

LI Ruomeng, TANG Qingqing

(Chongqing Key Lab of Mobile Communication Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, P. R. China)

Aiming at the problem that the Peak-to-Average Power Ratio(PAPR) is too high for the Filter Bank Multicarrier/Offset Quadrature Amplitude Modulation(FBMC-OQAM) system, a dual layered iterative partial transmit sequence algorithm in FBMC-OQAM system was proposed. Based on the traditional iterative partial transmit sequence algorithm, the proposed algorithm improves the search method, divides the phase factors into parity vectors to iterate, thus expandsing the search scope of the algorithm. Moreover, combined with the overlapping characteristics of FBMC-OQAM system, it uses the overlap between the data blocks. The proposed algorithm takes the phase factor vector that minimizes the PAPR of the sum of the signal after the current symbol block and the signal in the register window as the optimum phase factor vector, so as to improve the performance of the PAPR without increasing the amount of calculation. The simulation results show that the PAPR suppression effect of the improved dual layered iterative partial transmit sequence algorithm is significantly better than that of the traditional algorithm, the bit error rate is lower than that of the traditional algorithm, and the computational complexity is significantly lower than that of the partial transmission sequence algorithm.

multi-carrier filter bank/quadrature amplitude modulation; peak to average power ratio; iterative partial transmit sequence algorithm

s：The Changjiang Scholars and Innovative Team Development Program (IRT1299); The Chongqing Municipal Science and Technology Commission Key Laboratory of Special Funded Projects (cstc2013yykfA40010)

TN92

A

1673-825X(2017)05-0625-08

李若梦(1993-)，女，陕西渭南人，硕士研究生，主要研究方向为无线个人通信。E-mail:563282521@qq.com。

唐青青(1990-)女，河南项城人，硕士研究生，主要研究方向为移动通信。E-mail: 1548830778@qq.com。

2017-05-08

2017-09-11

李若梦 563282521@qq.com

长江学者和创新团队发展计划(TRT1299)；重庆市科委重点实验室专项经费(cstc2013yykfA40010)

10.3979/j.issn.1673-825X.2017.05.008