考虑微观形貌时平面型推力滑动轴承润滑性能数值研究

,

(华东理工大学机械与动力工程学院,上海 200237)

考虑微观形貌时平面型推力滑动轴承润滑性能数值研究

李姗姗,安琦

(华东理工大学机械与动力工程学院,上海200237)

选择平面型推力滑动轴承为研究对象,通过对粗糙表面的数值模拟,基于雷诺方程,构建了考虑微观形貌时的平面型推力滑动轴承润滑性能的计算模型。运用Matlab软件编程,针对一个具体的算例,采用数值计算研究了轴承工作时推力环旋转一周过程中最大油膜压力、承载能力、最小油膜厚度等参数的变化规律,发现其润滑性能与表面形貌有关;研究了转速、表面粗糙度等因素对推力滑动轴承润滑性能的影响规律,绘制了在保持全油膜润滑状态下速度和承载能力、摩擦力矩之间的关系曲线,并对这些曲线进行了分析。

推力滑动轴承; 微观形貌; 润滑性能; 数值模拟

流体动压推力滑动轴承是承受轴向推力并限制轴作轴向移动的滑动轴承,广泛应用在水利、电力、机械及化工等工业领域。推力滑动轴承主要有4种结构:平面多沟推力轴承、 斜-平面推力轴承、阶梯面推力轴承和可倾瓦块推力轴承。其中,平面型推力滑动轴承在中小载荷场合应用十分广泛,其主要依靠表面微观形貌在相对运动过程形成一层很薄的油膜来承受载荷,表面形貌如何影响其润滑性能,至今仍然是工程界面临的需要解决的问题。

芦定军等[1]研究了瓦块倾斜角和瓦块最小油膜厚度对推力滑动轴承性能的影响,得出了最佳的推力瓦块倾斜角和最佳的最小油膜厚度值。高磊等[2]研究了瓦高比、长宽比和瓦块数对轴承润滑性能的影响规律,指出了推力滑动轴承最佳结构参数的确定方法。朱旭辉[3]研究了不同转速和不同黏度对油膜压力的影响,结果表明,转速越高,油膜黏度越大,柱面弧形油楔推力滑动轴承的动压承载能力就越高。Ettles等[4]比较了大型可倾瓦推力滑动轴承在3种不同支撑方式下的各项性能,得到了最优结构设计。

也有研究者在考虑表面形貌的条件下研究润滑问题。Hu等[5]提出一种基于时间序列模型、数字滤波技术和Johnson转换系统的粗糙表面模拟方法,分别模拟了各向同性与各向异性、高斯与非高斯分布条件下具有不同形式自相关函数的粗糙表面。王晓雷等[6]研究了表面微坑分布对材料摩擦学性能的影响,认为适当的表面织构有助于在接触表面间建立或局部建立动压润滑薄膜。Jian等[7]研究了纵向粗糙度对薄膜混合弹流润滑的影响,指出拥有纵向粗糙度的表面能形成润滑油膜。周琼[8]通过基于对轴和密封唇的三维随机粗糙表面的模拟,提出并构建了一种能够同时考虑密封唇和轴表面微观形貌、密封唇过盈量、密封唇的弹性变形等因素的流体动压润滑性能的数值模拟计算方法。Wang等[9]利用虚拟变形技术,研究了微观表面织构与润滑性能的关系,认为润滑性能不仅与表面粗糙度有关,还跟表面形貌和纹理有重要关系。Gherca等[10]研究了表面织构对稳态和瞬态润滑状态下推力轴承动力润滑性能的影响,指出将表面纹理放置在轴承转子上可在一定条件下改善润滑性能。段京华等[11]研究了轴承表面形貌和润滑剂黏温效应对燃油泵滑动轴承润滑性能的影响,指出表面形貌和热效应对燃油泵滑动轴承的润滑性能存在直接影响。卢宪玖等[12]采用涉及轴承滚道和滚球体面上的余弦粗糙波数学模型,考察了表面粗糙度对角接触球轴承的压力和膜厚的影响。

综上可以看出,以往对推力滑动轴承的研究大多集中于对瓦块式推力滑动轴承润滑性能的研究,对平面型推力滑动轴承润滑性能的研究较少。在考虑微观表面形貌方面的研究中,大多数研究的是规则纹理或采用规则分布的粗糙表面,而实际中应用的平面型推力滑动轴承的微观表面形貌是随机分布的。因此,在考虑微观形貌前提下研究平面型推力滑动轴承润滑性能很有必要。

1 计算模型构建

1.1平面型推力滑动轴承工作原理

平面型推力滑动轴承的结构原理如图1所示,主要由轴、推力环、轴承衬、轴瓦构成。工作时,推力瓦固定,推力环以相对角速度ω旋转。根据流体动力润滑基本理论,由于两接触的粗糙表面存在随机分布的微凸体,从微观上看接触区域内将离散分布着许多微小的收敛楔形间隙,两表面的相对运动将润滑油带进这些微小的收敛形间隙,从而建立起一层润滑油膜,产生流体动压润滑。

图1 平面型推力滑动轴承三维结构图(a)及二维剖面图(b)Fig.1 Three dimensional structural drawing (a) and two-dimensional cross-section (b) of planar thrust bearings

1.2三维粗糙表面模拟方法

要对推力滑动轴承进行润滑性能研究,首先要构建微观粗糙表面。根据文献[5]中的理论,粗糙表面可以视为一个平稳的、离散的随机过程,即为一个个离散的数值,所对应的离散化自相关函数形式如下:

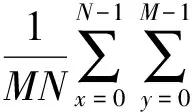
(1)

式中:τx,τy分别为x,y方向采样点间距;z(x,y)为坐标(x,y)处高度;M、N分别为x,y方向采样点个数。

生成具有指定自相关函数的粗糙表面的步骤如下:

(1) 利用计算机生成一个高斯分布白噪声二维随机序列η(x,y) ,计算其傅里叶变换A(ωx,ωy);

(2) 给定自相关函数:

(2)

式中:σ为表面均方根粗糙度;βx,βy分别为x,y方向上的相关长度。对式(2)进行傅里叶变换可求得输出信号功率密度谱函数G(ωx,ωy);

(3) 计算滤波器的传递函数H(ωx,ωy);

(4) 计算输出序列的傅里叶变换Z(ωx,ωy);

(5) 对Z(ωx,ωy)进行傅里叶逆变换,从而求得表面微观形貌分布函数z(ωx,ωy)。

1.3润滑力学模型

推力环和推力瓦的接触面均考虑为随机粗糙表面,如图2所示,由于表面粗糙度的存在,两个相对滑动的表面间从微观上将离散分布着微小楔形间隙。根据流体润滑力学的基本理论,将形成离散的流体动压区域,若这种流体动压足够大就形成流体动压润滑,其控制方程可用雷诺方程表达,其三维普遍形式为

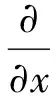
12ρ(V1-V2)

(3)

式中:x表示周向坐标;y表示径向(膜厚方向)坐标;p为压力;ρ为润滑油密度;μ为润滑油黏度;h为两个表面之间的间隙(即润滑膜的厚度);U1,U2分别为推力环和推力瓦周向速度;V1,V2分别为推力环和推力瓦法向速度。

由于推力滑动轴承工作时推力环旋转,推力瓦静止,稳定运转时,推力滑动轴承的温度基本不变,润滑油黏度和密度在润滑区域可以看作常数,不考虑法向速度V1、V2的变化。

式(3)可以简化为

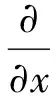
(4)

对于推力滑动轴承,将方程(4)采用柱坐标系进行表达:

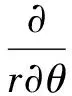
(5)

式中:r表示径向坐标;θ表示周角坐标;U=ωr,ω为轴颈旋转角速度。

图2所示为推力滑动轴承滑动面间隙示意图,其间隙表达式如下:

h(x,y)=h0+z1(x,y)+z2(x,y)

(6)

其中:h0为中心油膜厚度;z1、z2为膜厚的随机部分,即粗糙表面在该点的轮廓高度。

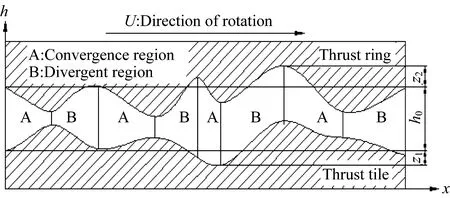
图2 收敛形间隙示意图Fig.2 Schematic diagram of convergence-shaped gap

为减少变量个数,方便求解,对雷诺方程进行量纲为一化,各参数的量纲为一表达式如下:

(7)

p是未知变量,事先难于选定某一特征p值作为其相对单位,以某一未定的p0暂表之,则量纲为一压力为

(8)

将以上量纲为一形式代入雷诺方程,得到量纲为一雷诺方程:

(9)

(10)

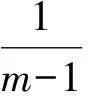
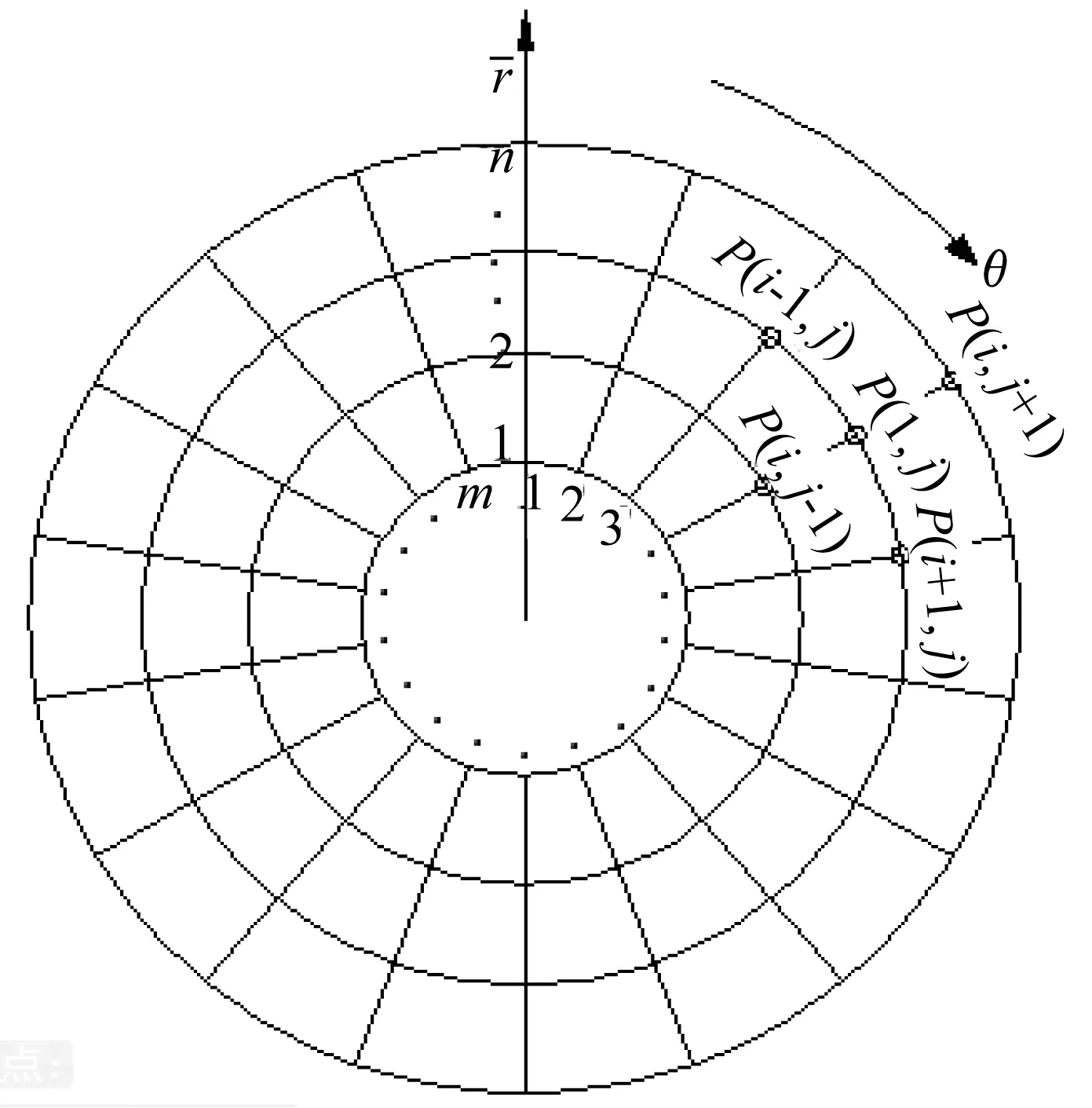
图3 网格划分示意图Fig.3 Schematic diagram of meshes generation

为便于编程求解,利用差分法将偏微分方程离散化,即将连续方程中的偏导用差商表示,最后得到离散化的偏微分方程表达式为

Ai,jPi+1,j+Bi,jPi-1,j+

Ci,jPi,j+1+Di,jPi,j-1-Ei,jPi,j=Fi,j

(11)

其中:

i,j分别为周向和径向节点坐标。

引入边界条件:

j=1,j=n,p(i,j)=0

对于方程得出的迭代计算结果,用如下的收敛准则进行收敛性判断:

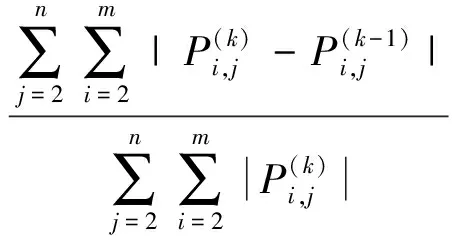
(12)

其中:k为迭代次数;取计算精度ε=10-6。

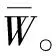
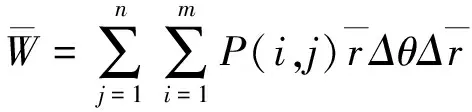
(13)

(14)

具体计算流程如图4所示。

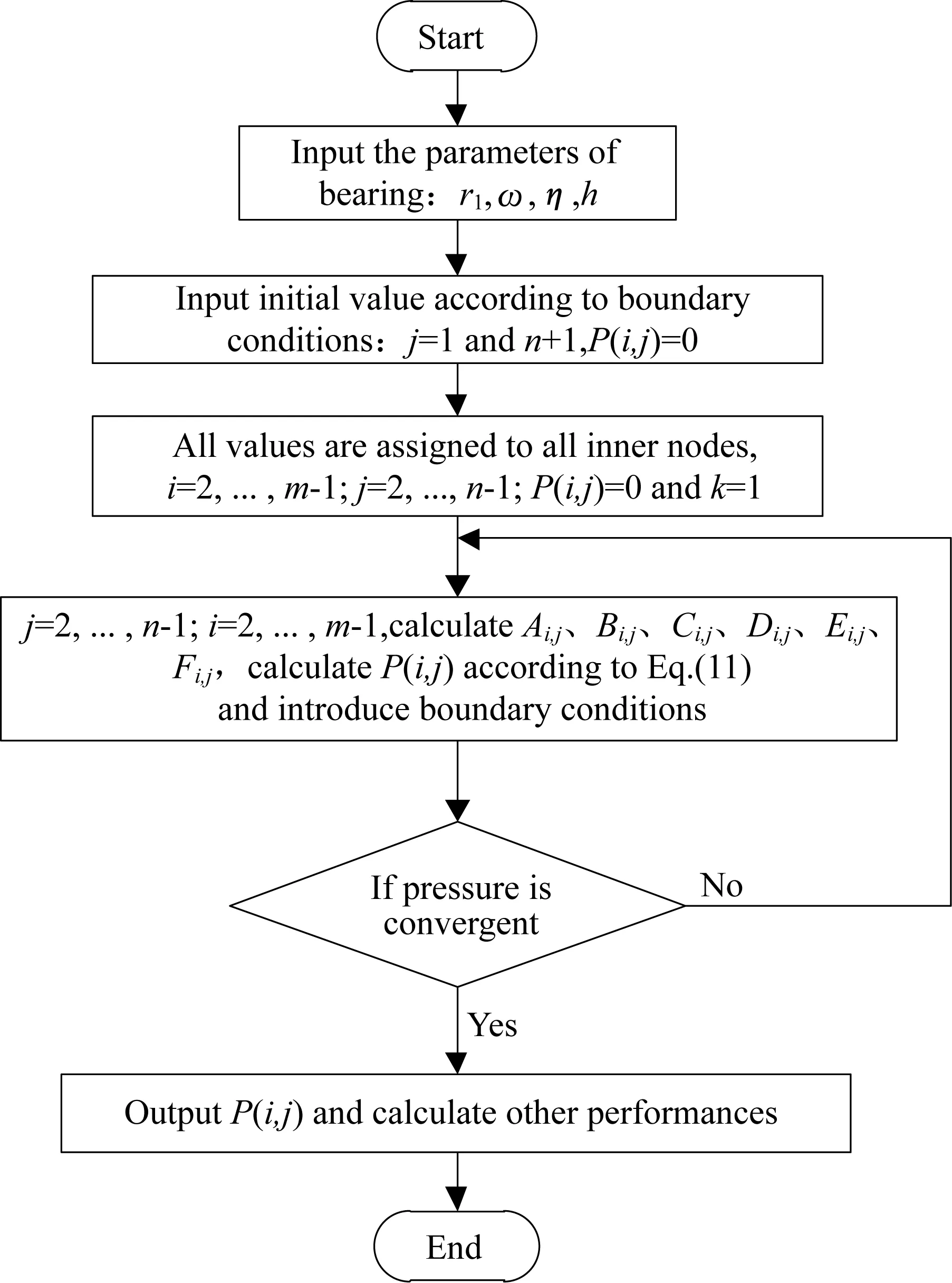
图4 计算流程图Fig.4 Calculation flow chart

2 算例研究

轴承表面经过磨削、研磨加工,其表面粗糙度Ra一般为0.1～3.2 μm。应用上述理论,以某推力滑动轴承为例,模拟推力环和推力瓦的粗糙表面,并计算轴承的润滑性能,所取的计算参数如表1所示。粗糙表面的模拟结果分别如图5、图6所示。

用有限差分法对雷诺方程进行离散时,根据接触面尺寸,划分计算区域所取网格数m×n为400×300。图7(a)和7(b)分别为润滑区域量纲为一油膜压力分布和油膜厚度分布图,图8(a)和8(b)分别为轴承中径处二维量纲为一油膜压力和油膜厚度曲线图,可以看出,当计入微观表面形貌时,油膜压力和油膜厚度分布具有不规则性,且在相对间隙小处会出现压力峰值。

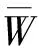
表1 推力轴承计算参数表

Rz1andRz2mean the root-mean-square roughness of thrust tile surface and thrust ring surface,respectively

图5 推力瓦表面Fig.5 Surface of thrust tile

图6 推力环表面Fig.6 Surface of thrust ring

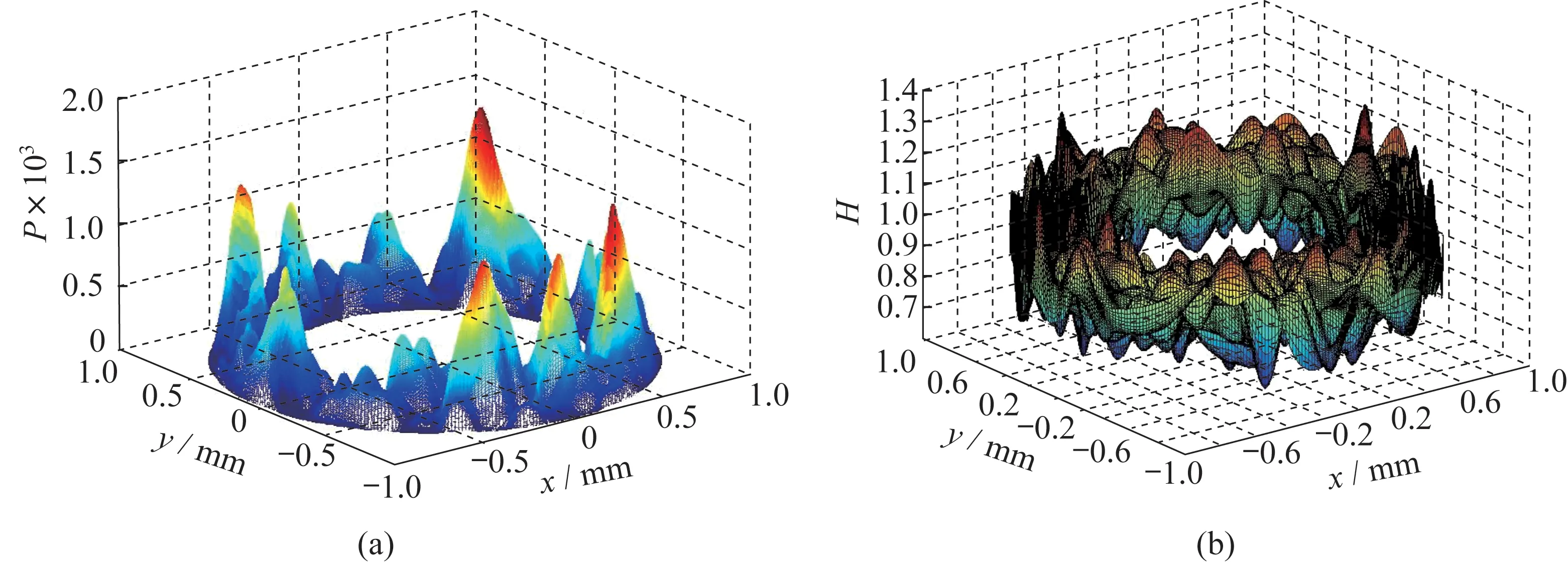
图7 量纲为一的油膜压力(a)和膜厚(b)三维分布图Fig.7 Three-dimensionless oil film pressure (a) and thickness (b) distribution

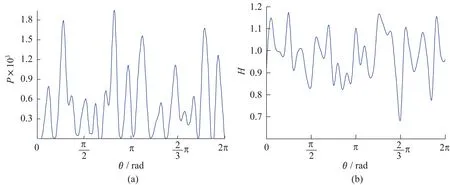
图8 轴承中径处量纲为一油膜压力(a)和膜厚(b)二维分布图Fig.8 Two-dimensionless oil film pressure (a) and thickness (b) distribution

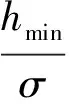
取载荷F=150 N,推力环表面粗糙度Ra1=0.1 μm,推力瓦表面粗糙度Ra2为0.05、0.1、0.2 μm,计算转速为600～2 000 rad/min时,推力轴承的承载能力达到额定载荷时的最小油膜厚度和膜厚比。图10(a)、10(b)分别示出了不同的两表面粗糙度下,转速与最小油膜厚度、膜厚比之间的关系。可以看出,当载荷一定时,随着转速的增大,最小油膜厚度和膜厚比均增大。由图10(a)可知,当转速相同时,两个表面粗糙度差异越大,形成的油膜厚度越大。由图10(b)可知,表面粗糙度越大,膜厚比越小,越难以形成全油膜润滑。

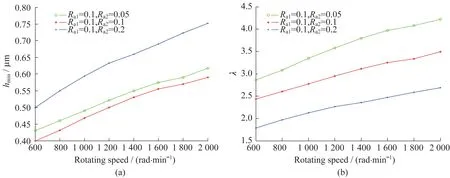
图10 转速对最小油膜厚度(a)和膜厚比(b)的影响Fig.10 Influences of speed on minimum oil film thickness and film thickness ratio (b)

在保持膜厚比λ=3的条件下,分别取转速为1 000、1 400、1 800 rad/min,得到承载能力和摩擦力矩与两表面综合粗糙度之间的关系,如图11(a)、11(b)所示。在相同的转速下,推力轴承在液体润滑状态下的承载能力W和摩擦力矩Tf随着表面粗糙度的增大而减小,转速越大,承载能力和摩擦力矩的下降幅度越大。当两表面综合粗糙度达到一定值时,承载能力很小,增大转速会增加摩擦力矩,而对提高承载能力效果甚微。

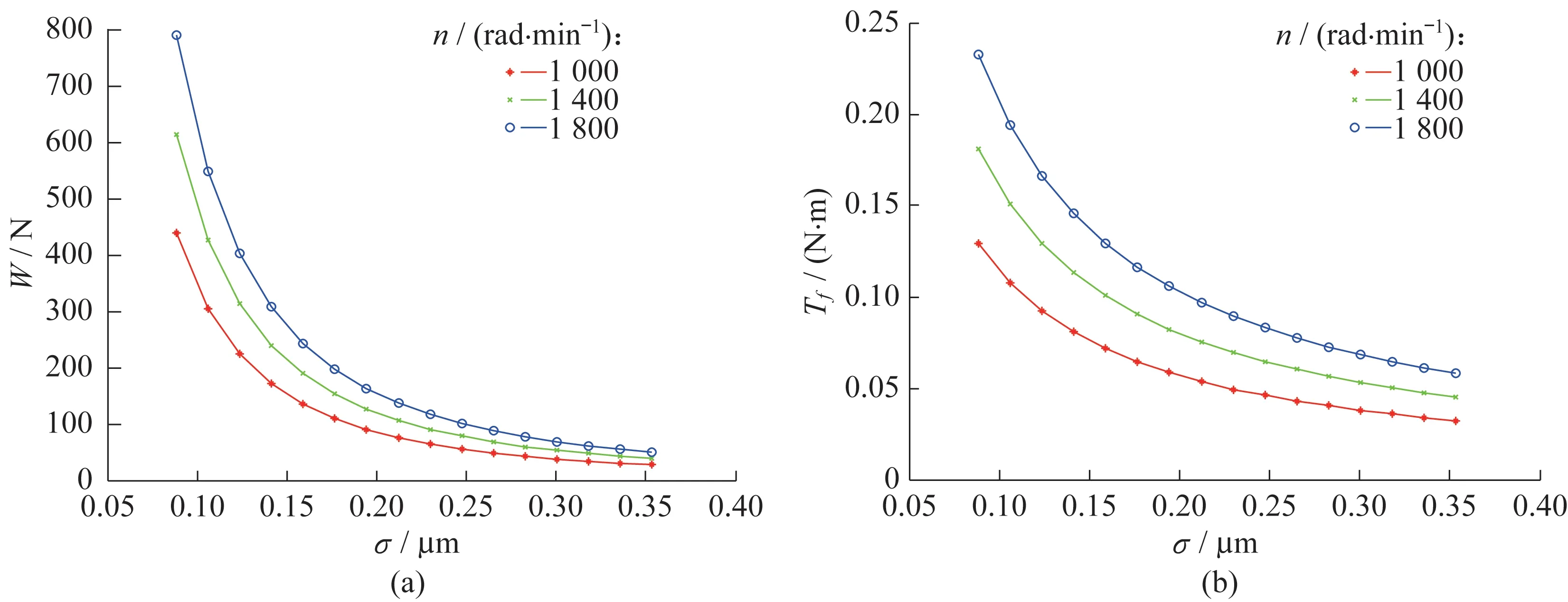
图11 表面粗糙度对承载能力(a)和摩擦力矩(b)的影响Fig.11 Influences of surface roughness on carrying capacity (a) and friction torque (b)

3 结 论

(1) 以平面型推力滑动轴承为研究对象,通过对推力环和推力瓦两个粗糙表面的数值模拟,基于雷诺方程,构建了两个粗糙表面间润滑力学计算模型。通过对模型的量纲为一化和离散化,运用Matlab语言编制计算程序,成功实现了在考虑表面微观形貌时对平面型推力滑动轴承的润滑性能计算。

(2) 应用所建立的计算方法,通过一个具体的算例,研究了推力滑动轴承在旋转一周过程中最大油膜压力、最小油膜厚度、承载能力、摩擦力矩的变化过程,得出了具体的变化曲线,发现平面型推力滑动轴承的润滑性能与表面形貌有关;研究了在某一定载荷作用下轴承运转过程中,转动速度和表面粗糙度对滑动面润滑性能的影响规律,发现当载荷一定时,在相同转速下,两个润滑面的表面粗糙度差异越大,产生的油膜厚度越大,但随着表面粗糙度的增大,膜厚比减小,越难以形成全油膜润滑;研究了在保持全油膜润滑的条件下,转动速度和表面粗糙度对轴承承载能力和润滑面摩擦力矩的影响规律,发现当膜厚比一定时,在相同的表面粗糙度下,承载能力随着转速的增大而增大,当两表面综合粗糙度达到一定值时,转速增大不仅无法提高承载能力,而且会增加摩擦力矩。

[1] 芦定军,杨建军,黄德全,等.推力滑动轴承瓦块倾角的数值研究[J].润滑与密封,2004(3):40-41.

[2] 高磊,刘俊,安琦,等.推力滑动轴承结构参数的数值研究[J].华东理工大学学报(自然科学版),2007,33(6):874-877.

[3] 朱旭辉.基于CFX的柱面弧形油楔推力滑动轴承仿真分析[J].机械工程师,2014(8):144-146.

[4] ETTLES C M,LPEZ G D,BORGN A H.Optimized design of a large reversible thrust bearing[J].Journal of Tribology,2016,138(4):041701.

[5] HU Y Z,TONDER K.Simulation of 3-D random rough surface by 2-D digital filter and fourier analysis[J].International Journal of Machine Tools & Manufacture,1992,32(1):83-90.

[6] 王晓雷,王静秋,韩文非.边界润滑条件下表面微细织构减摩特性的研究[J].润滑与密封,2007,32(12):36-39.

[7] ANDREW J,DUMONT M L.The influence of longitudinal roughness in thin-film,mixed elastohydrodynamic lubrication[J].Tribology Transactions,2006,49(2):248-259.

[8] 周琼.唇形密封圈润滑性能及对转子动力学性能影响研究[D].上海:华东理工大学,2013.

[9] WANG Q J,ZHU D.Virtual texturing:Modeling the performance of lubricated contacts of engineered surfaces[J].Journal of Tribology,2005,127(4):722-728.

[10] GHERCA A,FATU A,HAJJAM M,etal.Influence of surface texturing on the hydrodynamic performance of a thrust bearing operating in steady-state and transient lubrication regime[J].Tribology International,2016,102:305-318.

[11] 段京华,孙军.计及表面形貌和热效应的燃油泵滑动轴承润滑分析[J].机械设计,2016(6):1-5.

[12] 卢宪玖,王优强,律辉,等.微观表面形貌对角接触球轴承热弹流润滑的影响[J].润滑与密封,2014,39(6):49-55.

NumericalStudyonLubricationPerformanceofPlanarThrustBearingConsideringMicrocosmicTopography

LIShan-shan,ANQi

(SchoolofMechanicalandPowerEngineering,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

Based on the numerical simulation of the rough surfaces and Reynolds equation,the calculation model for planar thrust sliding bearing with considering microcosmic topography was established.By use of a specific example,the changes of the maximum oil film pressure,bearing capacity and minimum oil film thickness of the thrust bearing during rotating were numerically calculated by using Matlab programming.The results show that the lubricating performance of planar thrust sliding bearing is relative with its microscopic morphology.The influences of rotation speed and surface roughness on the lubrication performance of thrust sliding bearing were studied in detail.The curves of relations between rotation speed,bearing capacity and friction torque under the condition of full lubrication film were obtained,and these correlation curves were analyzed.

planar thrust sliding bearing; microscopic morphology; lubricating performance; numerical simulation

TH117.2

A

1006-3080(2017)05-0733-07

10.14135/j.cnki.1006-3080.2017.05.020

2017-01-09

上海市设计学Ⅳ类高峰学科资助项目(DA17014)

李姗姗(1992-),女,浙江人,硕士生,研究方向为工程摩擦学。

安 琦,E-mail:anqi@ecust.edu.cn