大规模MIMO中基于低复杂度雅克比预编码算法及实现
王 雷
(南京理工大学电子工程与光电技术学院 江苏 南京 210000)
大规模MIMO中基于低复杂度雅克比预编码算法及实现
王 雷
(南京理工大学电子工程与光电技术学院 江苏 南京 210000)
迫零线性预编码可以获得接近最优的系统容量,不同于传统MIMO系统,大规模MIMO将会配置成百根天线,随着天线数量增加,使得迫零线性预编码矩阵求逆计算复杂,不利于在应用中实现。为了减小线性预编码计算复杂度,提出基于低复杂度的雅克比迭代算法,该算法通过线性迭代,避免了矩阵求逆运算,减少了计算量。为了更进一步的减少计算时间,提出基于统一计算架构的异构多核并行算法,该方法利用GPU具有多核多线程结构特点,实现了异构多核并行计算。仿真结果表明,基于低复杂度雅克比预编码算法可以达到迫零预编码算法性能,同时与传统的线性预编码相比,该算法的计算量更少、时间更短。
预编码 雅克比 统一计算架构 迫零 异构多核
0 引 言
和传统的MIMO系统不一样,大规模MIMO系统在基站端配置了大量的天线单元(几百根)同时对小区中的多个用户同时传输数据。理论证明大规模MIMO系统比传统的小规模MIMO系统提高了几个数量级的系统容量和能效,该技术有望用在未来5G无线通信系统当中[1]。
然而,在实际的大规模MIMO系统中,面临着许多挑战。例如,在下行链路多用户系统中,为了消除其他用户对某个用户的干扰,该用户必须做均衡处理[2]。然而,在用户端做复杂的均衡处理,会使得用户设备能耗高。目前,pad、手机如何节约能效一直是一个难点,在实际当中,在用户端做复杂的均衡计算,往往是不切实际的。因此,有必要对发射端做预编码(尽管会增加基站负荷),将会大大减少用户端均衡复杂度。最优的预编码是非线性脏纸预编码DPC(dirty paper precoding)[3]。然而在大规模MIMO中,由于维度很大,脏纸预编码算法难以实现。线性预编码中,有向量转置预编码、格约简辅助预编码和迫零预编码[4-5],该三种线性预编码在低维度时,计算量少,然而随着天线数量增加,其复杂度将大大增加。因此,如何减少计算复杂度同时获得接近最优的系统容量,是一个迫在眉睫的问题。
与传统的中心处理单元CPU不同,图形处理单元GPU提供了大量的并行架构,GPU中大多数晶体管是用来处理算术逻辑单元ALU(Arithmetic Logic Unit),而不是像CPU那样大多用来缓存和数据流控制[6-9]。理论测试表明,显卡Geforce GT620可以到达到每秒约120亿次浮点计算。在无线通信系统中,基于GPU加速是一个研究热点,尤其在加速仿真和软件无线电SDR(software defined radio)。
本文提出了基于低复杂雅克比算法。该算法通过迭代的方法,避免了矩阵求逆计算,分析表明本文提出的算法比传统求逆迫零预编码算法减少一个数量级的计算量,同时获得了和迫零预编码算法一样的性能。为了更进一步地减少计算时间,提出了基于统一计算架构的异构多核并行算法,该方法利用GPU具有多核多线程结构特点,实现了异构多核并行计算。仿真结果表明,基于低复杂度雅克比预编码算法可以达到迫零预编码算法一样的性能,同时与传统的线性预编码相比,该算法的计算量更少,时间更短。
1 系统模型
我们考虑单基站,多用户大规模MIMO系统,如图1所示,基站端配置天线个数为N,用户数为K,每个用户配有一根天线,其中N≥K。在下行链路系统中,基站同时对K个用户传输数据,可以表示为:
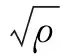
(1)
其中,ρ表示的是信噪比SNR,H∈CK×N表示平坦衰落瑞利信道矩阵,该矩阵中的每个元素服从CN(0,1),n=[n1,n2,…,nK]T表示加性高斯白噪声,服从CN(0,1),用户端接收信号为y=[y1,y2,…,yK]T。x是预编码之后的发射数据。
x=Ps
(2)
其中P是预编码矩阵,s=[s1,s2,…,sK]T是传输给K个用户的信息,且x满足:
E{‖x‖2}=K
(3)
当发射端天线数N增大时,信道矩阵H中的列向量趋近于正交,因此利用简单的线性预编码技术可以获得接近最优的容量。
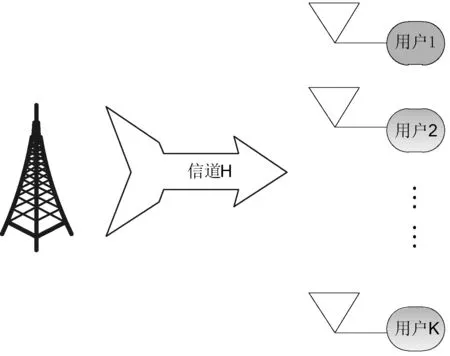
图1 多用户MIMO系统
2 低复杂度雅克比预编码实现
本小节,首先简要介绍一下经典迫零ZF(zero forcing)算法,其次提出了基于雅克比迭代算法,然后介绍了基于CUDA的并行架构,最后对提出的算法进行了复杂度分析。
2.1 迫零预编码原理
在基站端做迫零预编码,可以消除用户之间的干扰,经典的迫零预编码矩阵PZF可以表示成如下形式:
PZF=βH+=HH(HHH)-1=HHG-1
(4)
其中HH表示信道矩阵H的厄米特共轭转置,H+表示矩阵H的伪逆矩阵,G=HHH,β表示每个用户的平均发射功率,我们可设β为:
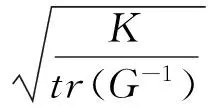
(5)
根据式(1)、式(2)、式(4)和式(5),可以得到等效信道:
Heq=βHHHG-1
(6)
由式(4)可知道PZF需要矩阵求逆,其计算复杂度为O(K3),当用户数增多时,其将会大大增加基站的负荷。
假设基站可以完全获得信道状态信息,对于任何用户k,其信干噪比SINR可表示为:
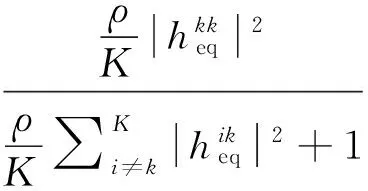
(7)
利用式(4)可得其信干噪比为:
(8)
经典迫零矩阵使得其他用户对某个用户的干扰完全消除。在利用基于雅克比迭代求解时,如果迭代次数不够,会使得式(7)中分母的第一项不为0,会降低信干噪比,使得误码率增加。通过仿真表明,当迭代次数为3以上时,性能就已经很接近迫零算法。
最后根据式(7),可得到总的系统频谱效率为:
(9)
2.2 基于雅克比迭代预编码算法
雅克比迭代算法(Jacobi)是用来求解如下形式的线性方程组:
Ay=b
(10)
其中矩阵A是大小为N×N的矩阵,b是已知的大小为N×1向量,y是所求的列向量。不同于传统的直接求解y=A-1b,雅克比算法通过如下迭代求解y:
yk+1=-D-1(L+U)yk+D-1b
(11)
其中A=D+L+U,矩阵D为矩阵A的对角矩阵,矩阵L为矩阵A的严格下三角矩阵,矩阵U为矩阵A的严格上三角矩阵,yk+1表示向量y的第k+1次迭代。
由式(2)和式(4),向量x可表示为:
x=Ps=βHHG-1s
(12)
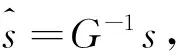
引理1矩阵G可逆且是正定矩阵
由于G=HHH,GH=HHH,因此G=GH,说明矩阵G厄米特共轭转置。对于任意非零列向量α:
αHGα=(αHH)(αHH)H≥0
(13)
在瑞利信道矩阵H下,信道H中列向量趋于正交,因此矩阵H是列满秩的,因此αHGα>0,说明矩阵G可逆且是正定矩阵。
2.3 异构多核并行架构
异构多核架构通常包含主机端(CPU)和设备端(GPU)。主机端通常处理和控制级联算法,而设备端含有大量的核,通常用来做并行计算。如图2所示。
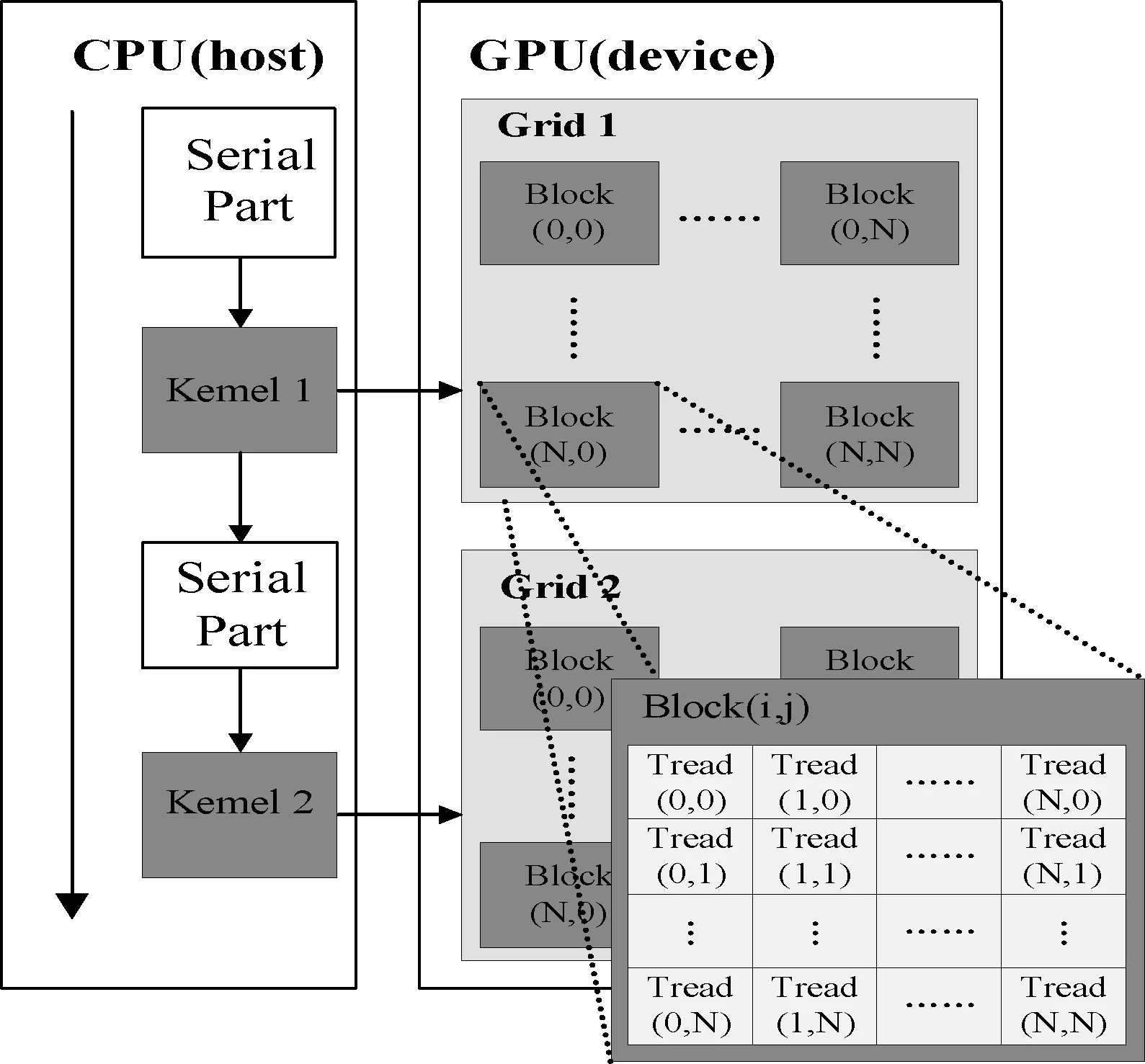
图2 异构多核架构
统一计算架构CUDA(Compute Unified Device Architecture)是用来对GPU作并行计算的运算平台。我们可以把设备端的数据传输到主机端,也可以把主机端的数据传输给设备端,因此设备端和主机端之间的数据可以相互传输。首先把所处理的数据存在主机端,主机端把该数据传输到设备端中去,设备端对这些数据进行处理计算,计算后的值再传输到主机端中去,CUDA-GPU通常包含四种寄存器:全局寄存器、共享存储器、常量存储器和纹理存储器。由于共享内存嵌入在线程块中,可以提供最快的读写操作,每个线程块中的线程通过合作同步高效率的执行。
2.4 复杂度分析
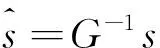
(14)
3 仿真分析
为了分析基于雅克比预编码算法性能,我们把该算法与经典迫零算法进行了比较。调制方式为64QAM,N×K=256×16,仿真结果如图3所示。
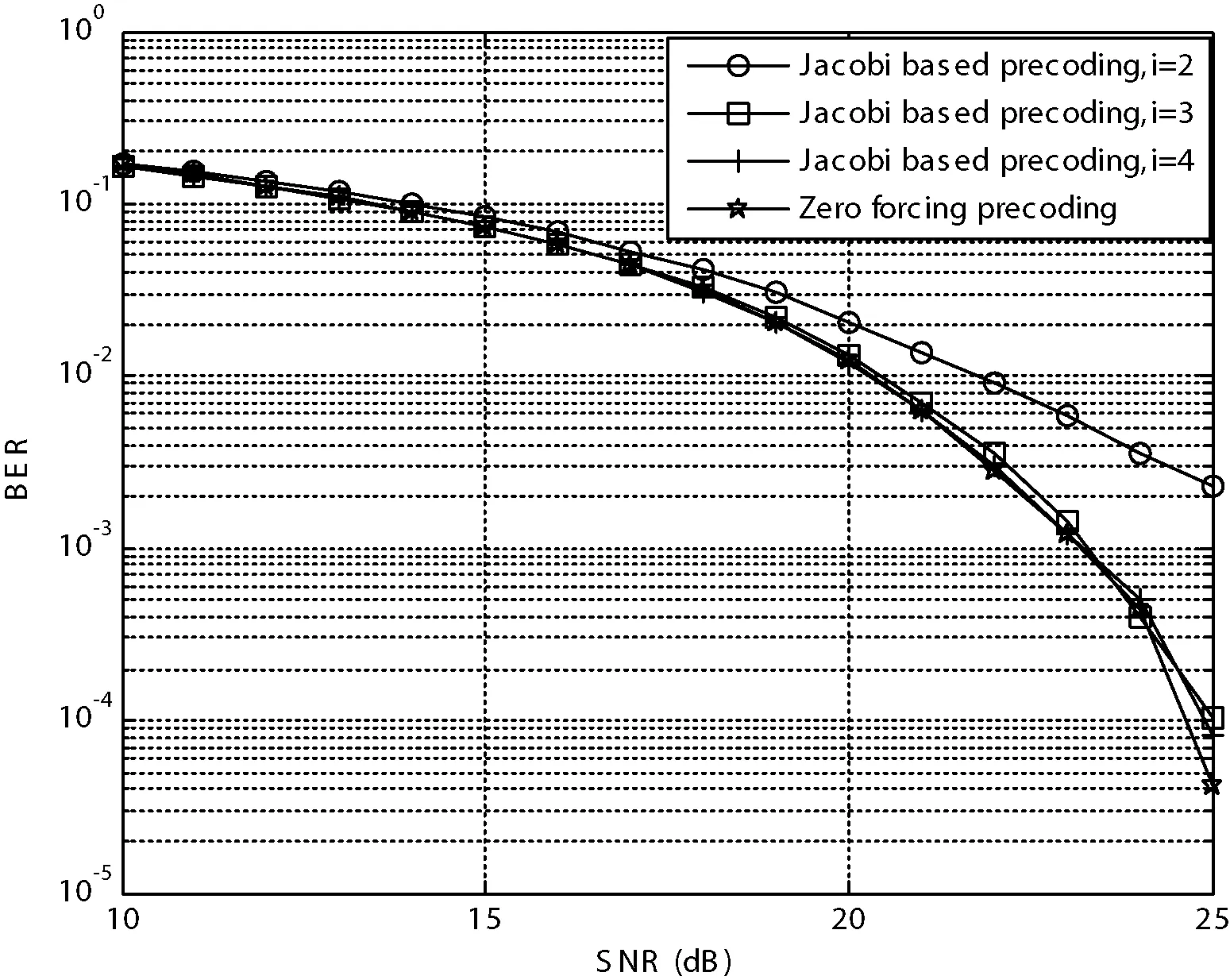
图3 迫零算法与基于雅克比算法性能分析对比
如图3所示,基于雅克比算法迭代次数为i=2时,在信噪比小于15 dB时,误比特率与迫零算法接近相同,当信噪比大于15 dB时,其误比特率要高于迫零算法,这是由于迭代次数过少,迭代出的值有较大的误差。然而,当迭代次数大于等于3时,其误比特与迫零算法趋于一致,这说明当迭代次数大于等于3时,就可以得到精确的值,说明了该算法收敛速度快,所需的计算量少。
考虑到基于雅克比预编码算法的并行性能,CPU是i3-3220四核内存,GPU是英伟达Geforce GT620,共包含32个CUDA核,如图4所示。

图4 基于CPU串行与GPU并行计算时间比较
从图4可以看出,相同矩阵维数,基于CPU计算时间比GPU并行计算时间要长,为了定量知道并行程序的执行速度相对于串行程序的执行速度加快了多少,我们定义其加速比,表示的是同一个任务在单处理器系统和并行处理器系统中运行消耗的时间比率。如图5所示给出了雅克比算法次数为2、3和4时的加速比,仿真结果表明,随着矩阵维数增大,其加速比越大,说明时间缩短的比例越大。
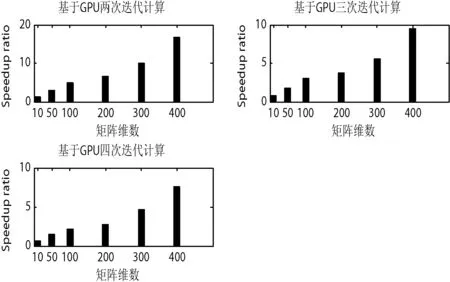
图5 基于GPU并行计算加速比
4 结 语
本文针对无线通信系统预编码计算量大的缺点,提出了基于低复杂雅克比算法。该算法通过迭代,避免了矩阵求逆计算,与传统的迫零算法相比,计算量减少了一个数量级,仿真结果表明该算法收敛速度快。当迭代次数大于等于3时,就可以得到精确的值,所需的计算量少。然后,我们提出了快速雅克比预编码算法并行实现。仿真结果表明并行计算可以大大减少计算时间,当矩阵维数越大,其获得的加速比越大,说明了相对于串行计算时间而言,并行计算所需要的时间更短。
[1] Rusek F,Persson D,Lau B K,et al.Scaling Up MIMO:Opportunities and Challenges with Very Large Arrays[J].IEEE Signal Processing Magazine,2012,30(1):40-60.
[2] Gao X,Dai L,Zhang J,et al.Capacity-approaching linear precoding with low-complexity for large-scale MIMO systems[C]//2015 IEEE International Conference on Communications (ICC),2015:1577-1582.
[3] Costa M.Writing on dirty paper[J].IEEE Transactions on Information Theory,1983,29(3):439-441.
[4] Gao X,Dai L,Hu Y,et al.Matrix inversion-less signal detection using SOR method for uplink large-scale MIMO systems[C]//Global Communications Conference.IEEE,2015:3291-3295.
[5] Prabhu H,Rodrigues J,Edfors O,et al.Approximative matrix inverse computations for very-large MIMO and applications to linear pre-coding systems[C]//Wireless Communications and NETWORKING Conference.IEEE,2013:2710-2715.
[6] 陈国良.并行计算[M].高等教育出版社,2011.
[7] 卢风顺,宋君强,银福康,等.CPU/GPU协同并行计算研究综述[J].计算机科学,2011,38(3):5-9.
[8] Yu D,He S,Huang Y,et al.A fast parallel matrix inversion algorithm based on heterogeneous multicore architectures[C]//IEEE Global Conference on Signal and Information Processing,2015:903-907.
[9] Mahfoudhi R,Mahjoub Z,Nasri W.Parallel Communication-Avoiding Algorithm for Triangular Matrix Inversion on Homogeneous and Heterogeneous Platforms[J].International Journal of Parallel Programming,2015,43(4):631-655.
LOWCOMPLEXITYJACOBIBASEDPRECODINGFORLARGE-SCALEMIMO
Wang Lei
(SchoolofElectronicandOpticalEngineering,NanjingUniversityofScienceandTechnology,Nanjing210000,Jiangsu,China)
Linear precoding techniques, such as zero forcing, can achieve the near optimal capacity. In contrast to traditional multiple input multiple output (MIMO), large scale MIMO installed hundreds of antennas, with the increasing numbers of antennas, zero forcing precoding involve the matrix inversion of large size with high computational complexity, which may cause difficulty for the realization of the application. To reduce the computational complexity of linear precoding, we propose a low complexity iterative algorithm based on the degree of Jacobi. This method realized through the linear iteration meanwhile avoided the matrix inversion. To further reduce the computation time, we propose a heterogeneous multicore parallel algorithm based on CUDA (compute unified device architecture), which leverage the Graphics Processing Unit (GPU) characteristic of multicores and multithreads to realize heterogeneous multicore architecture parallel computation. Experimental result demonstrates this proposed algorithm not only can achieve the same performance of zero forcing precoding, but also has less computation time and shorter time than traditional linear precoding.
Precoding Jacobi CUDA Zero forcing Heterogeneous multicore
TP391
A
10.3969/j.issn.1000-386x.2017.10.052
2017-01-03。王雷,副研究员,主研领域:通信与信息系统,信号信息处理。

