基于遗传交叉改进粒子群算法的充电站布局
张志宇 张会林 徐 辉 叶玉凤
(上海理工大学光电信息与计算机工程学院 上海 200093)
基于遗传交叉改进粒子群算法的充电站布局
张志宇 张会林 徐 辉 叶玉凤
(上海理工大学光电信息与计算机工程学院 上海 200093)
为了合理地规划城市电动汽车充电站布局,采用一种基于遗传交叉改进粒子群算法的寻优处理方案。在传统粒子群算法的基础上,引入局部极值对速度更新公式进行优化,采用自适应惯性权重,并且对当前种群的最优解和每个粒子最优解进行交叉操作产生新解。最后通过改进后算法对城市算例进行求解。结果验证了模型的有效性和准确性,表明改进算法在保持全局最优解的同时能提高70%收敛速度,有效降低总成本、提高便利性。
充电站 粒子群算法 遗传交叉 惯性权重
0 引 言
随着全球能源日趋紧张,生态环境日益恶化,新能源汽车的开发与应用问题已经成为各国汽车工业积极探索的焦点[1]。科技发展推动电动汽车电池技术的不断革新,使得许多欧美国家的电动汽车产业逐步规模化,中国也提出到2020年电动汽车保有量达到500万辆的发展计划[2]。因此,如何合理建设城市电动汽车充电站是现阶段所面临的首要任务。
目前,根据电动汽车充电的方式不同,电动汽车充电设施可以分为充电桩、充电站、换电站三种类型。杨现青等[3]简要分析了影响充电站布局规划的因素,考虑需求点分布,建立了收益最大化得非线性目标函数,但是只考虑到了建设和运营成本,忽略了用户的出行使用成本。应夏晖等[4]构建了基于充电站运营费用和用户充电费用的最小化模型,并用遗传算法进行了求解,遗传求解时采用固定的交叉变异概率,容易导致优良基因遭到破坏,从而陷入局部最优。冯超等[5]将标准遗传算法和交叉定位分配算法结合,形成一种新的混合算法,建立多种群协同进化搜索,但是由于种群数量多,可能造成算法计算量大和求解时间长的现象。Pan等[6]充分考虑城市电网的电网结构强度,在分析正常城市生活荷载变化的时空特征的基础上,提出了一种新的集中充电站布局策略。通过上述分析可知,虽然国内外有诸多文献对充电站的布局规划有过研究,但是考虑问题时并不是很全面,导致算法寻优的效果不是很理想。因此,本文建立了以经济性和便利性为目标的充电站模型,着重改进了传统的粒子群算法,并且引入遗传算法的交叉操作,利用改良后的算法对城市小区实例进行了验证求解,最终确定了充电站的规划布局。
1 影响充电站规划的因素
1.1 交通便利性
交通便利性主要体现在充电站附近的车道情况和车流量大小[7]。车道数量越多,车流量越大,则这点的交通便利性越好,充电站建设在这里能够利益最大化。当然,充电站的服务半径不宜过大或过小,太大了不能满足电动汽车的续航范围,太小了会导致过于集中以至于经济浪费。
1.2 充电需求量
充电需求量是指某一时间段特定区域内一定数量的电动汽车对电能的需求量,它直接影响充电站的地理位置选取和所需提供的功率的大小。只有建设充电容量足够大的充电站,才能满足待充汽车的需求量。因此,在对充电站进行规划之前,先应该计算出当前区域的电动汽车充电总负荷量。
1.3 经济性
经济性最优是充电站建设的重要目标之一。这主要表现在两个方面,一方面投资者希望投资建设费用和运行成本最低;另一方面用户希望能花费最少的费用获得最好的充电服务,具体体现在用户从需求点到达充电站所消耗的路上成本最小,它和需求点到充电站的距离成正比例关系。
2 选址模型
2.1 经济性
经济性主要从三个方面考虑,分别是初期投资固定成本、充电站运行成本和用户充电成本。
MinZ=Z1+Z2+Z3
(1)
(2)
式中:Z1为初期投资固定成本。F为购地、变压器、充电机及其他设备费用,m为充电站数目,n为充电站运行年限,r为投资回收率。
(3)
式中:Z2为充电站运行成本(维护费用、材料、人员工资等)。运行成本折算到初始投资费用,α为折算系数。
Z3=c·k·η·t(∑i∈I∑j∈JgijniDij)×10-4
(4)
式中:Z3为一年充电费用,c为一年天数365,k为每辆车每天充电次数,η为道路的曲折系数,t为汽车行驶每公里成本,I为充电需求点的集合,J为充电站的集合,gij为点i是否到充电站j充电(到j充电则为1,否则为0),ni为需求点i处需充电的汽车数量,Dij为点i到充电站j的直线距离。
约束条件:
(5)
式(5)的目的是保证在充电过程中只到一个充电站充电。
Dij≤Rj
(6)
式(6)的目的是充电半径应该大于汽车到充电站的距离。
∑i∈IPi≤Sje(Sj)cosφj
(7)
式中:Pi为到j充电站充电的电动汽车所需负荷,Sj为j充电站容量,e(Sj)为负载率,cosφj为功率因数。式(7)的目的是为了保证充电站的容量要大于到该充电站充电的电动汽车的所需总负荷。
2.2 交通便利性
在这里交通便利性以各用户到相应充电站的平均距离来表征,可以表征为:

(8)
充电站数目确定:
(9)
式(9)表示每天到充电站充电的所有汽车总充电需求量比上充电站充电的电动汽车的所需总负荷取整加1。
3 算法优化
粒子群算法(PSO)属于进化算法的一种,起源于对鸟群捕食的行为研究[8]。PSO算法的研究对象是一群随机粒子,它们有各自自己的属性(位置和速度)。这些粒子在空间中运动不断地更新自己,并且能够保留记忆每个粒子到当前为止所找到的最优位置以及所有粒子目前找到的全局最优位置。通过不断地更新速度和位置来获取最优解。
标准PSO算法的数学表述为:假设在一个q维搜索空间中有m个粒子,第i个粒子的位置向量和速度向量分别为:
xi=(xj1,xi2,…,xid)
vi=(vi1,vi2,…,vid)
通过式(10)、式(11)的每一次迭代来更新速度和位置:
vid(t+1)=w×vid(t)+C1×rand1×
[pid(t)-xid(t)]+c2×rand2×
[pdk(t)-xid(t)]
(10)
xid(t+1)=xid(t)+vid(t+1)
(11)
式中:vid(t+1)为更新后的速度,w为惯性因子(表示搜索范围),vid(t)为当前粒子速度,c1、c2为加速因子,rand1、rand2为[0,1]之间的随机数,xid(t)为当前粒子的位置,pid(t)、pgd(t)分别为粒子个体和全局的极值。xid(t+1)为更新后的粒子位置,xid(t)为当前粒子位置。
PSO算法规则简单,易于实现,收敛速度较快,特别是在算法运行的初期,但是它也有精度较低和容易陷入局部最优等缺点。在式(10)中,我们可以看到粒子的速度更新依赖于粒子自身的历史最优值pid(t)和全局历史最优值pgd(t)。这是在对全局进行搜索,忽略了对局部搜索的力度,一定程度上可能使算法不能取得正确的最优解。因此,在这里引入一个当代种群粒子的最优值pnd(t),它能更好地实现粒子和群体之间的信息交流。实现局部搜索和全局搜索的结合,提高精准度。更新后的速度公式为:
vid(t+1)=w×vid(t)+c1×α×rand1×
[pid(t)-xid(t)]+c2×rand2×
[pgd(t)-xid(t)]+c1×(1-α)×
rand1×[pnd(t)-xid(t)]
(12)
从式(12)可知,改进后的粒子速度与自身历史最优值pid(t)和全局历史最优值pgd(t)以及当代种群粒子的最优值pnd(t),理论上能够使PSO算法在保证收敛性的同时不陷入局部最优。其中α是一个可变权重值,体现了粒子的速度更新在参考粒子个体最优值的同时,一定比重地参考当代种群的最优值。当然,惯性权重也是一个和重要的参数,它直接影响算法的收敛精度,这里利用线性惯性权重,更新公式为:
w(t+1)=4w(t)(1-t)
(13)
遗传算法(GA)是一种模仿自然界生物进化的全局搜索优化方法,借鉴了达尔文的进化论和孟德尔的遗传学说[9]。遵循生物进化中优胜劣汰、适者生存的原理,通过编码与不断进化寻优,最终获得最优解函数值。在GA算法中,主要依靠选择、交叉和变异三个操作。交叉操作是遗传算法产生后代的主要方式,通过交叉实现父代个体的信息交流,这也是新个体的主要产生形式。而PSO算法中,粒子之间并没有直接通过信息交流来产生新的解。因此,在这里引入GA算法的交叉操作,对PSO算法的迭代结果(全局最优位置和每个粒子的最优位置)进行交叉操作,理论上能够利用信息交流产生新解,有效地跳出局部收敛。交叉公式为:
sid=rpid(t)+(1-r)pgd(t)
(14)
式中,sid(t)为进行完第t代交叉后的产生的第i个粒子的d维量,r为(0,1)之间的随机数。
算法步骤:
1) 初始化参数,设定粒子数量和最大进化代数,随机初始化粒子的位移,速度选取[0,1]的随机数,并且对惯性权重w,最大进化代数tmax个体最优解pid(t),全局最优值pgd(t)以及初代种群粒子的最优值pnd(t)进行设定。
2) 计算目标函数,并对初始种群进行评价,计算改进后的惯性权重,利用式(11)、式(12)对粒子进行位置速度更新。
3) 将该粒子的更新后新位置和原来的pid进行比较,若前者由于后者,则将pid替换;若pid优于pgd,则令pgd=pid。
4) 判断所有粒子是否迭代更新完毕,完毕则进行下一步操作,否则转到步骤2)继续。
5) 利用式(14)对已经迭代完成的粒子进行遗传交叉操作。
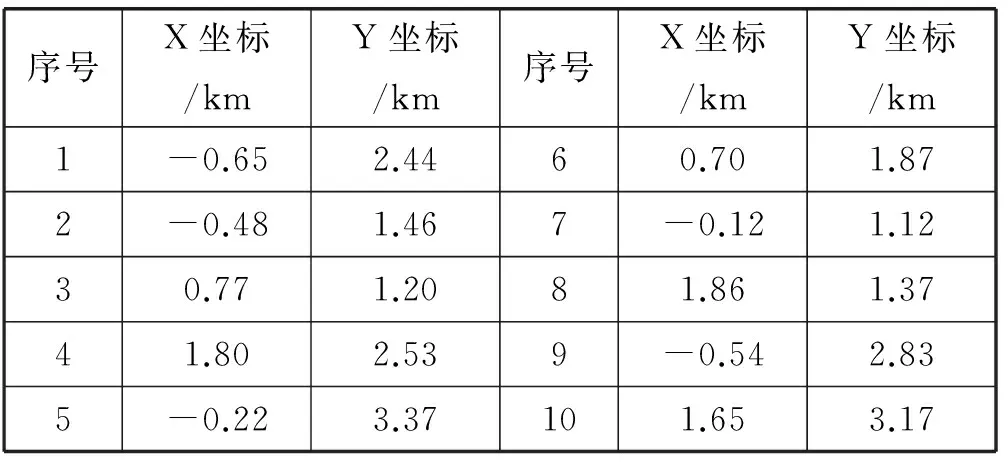
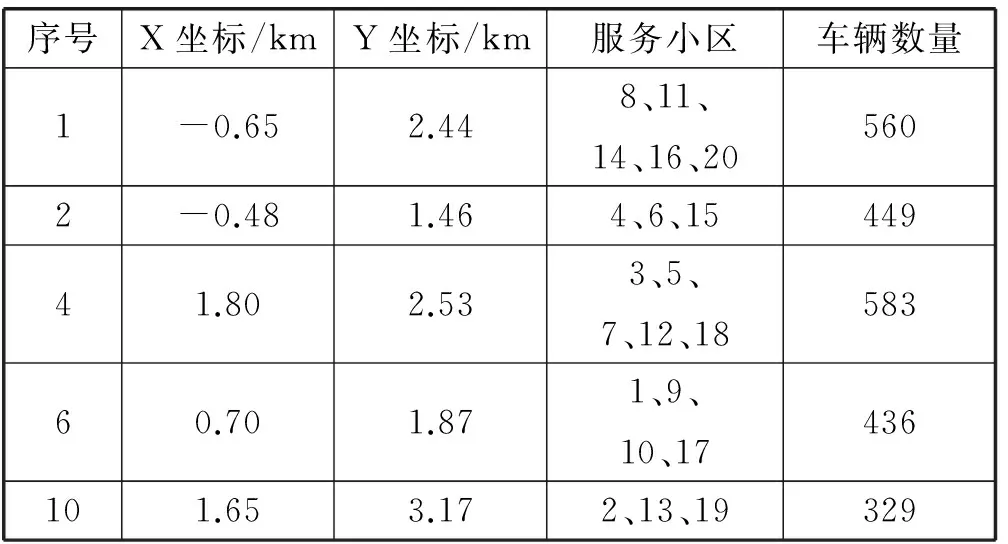
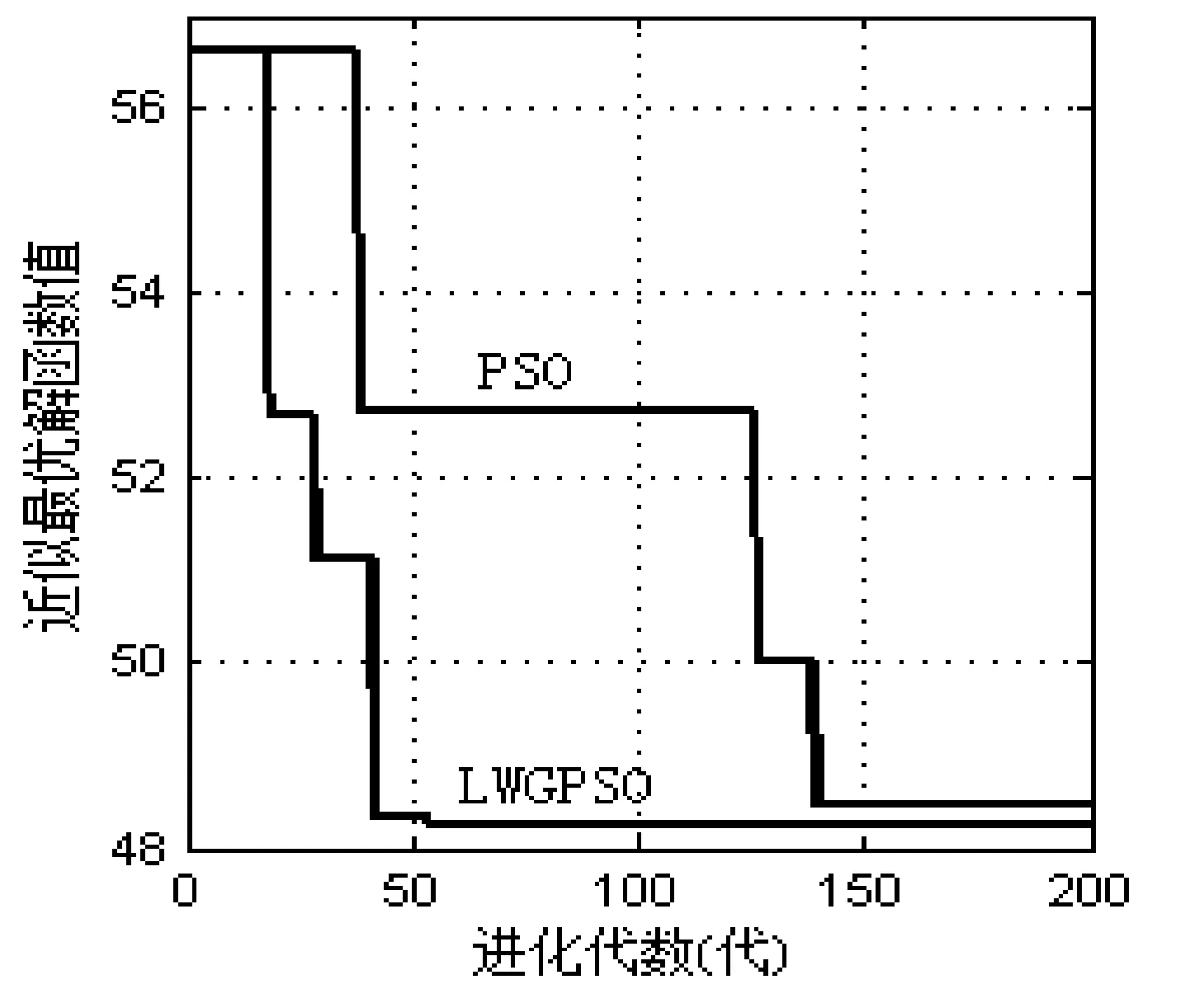
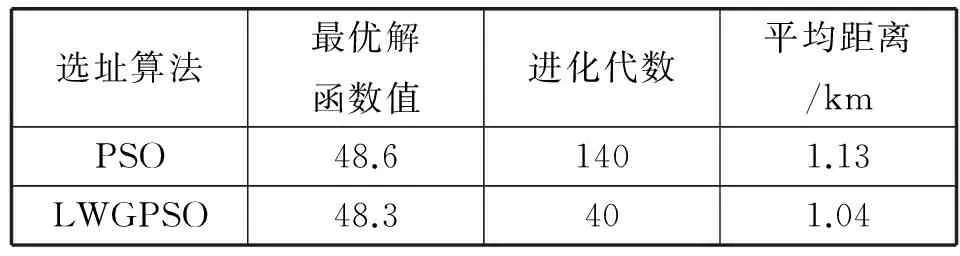
6) 如果t 为验证本文所提出算法(简称LWGPSO)的可行性和有效性,利用以下选址实例进行测试。上海市一个规划区面积为13 km2,在规划时间内电动汽车的保有量为2 357辆,通过分析汽车的分布情况,确定划分为20个充电需求小区。小区的几何坐标中心及电动汽车数量如表1所示。 表1 小区坐标及电动汽车数量 续表1 在规划区内建设充电站为电动汽车提供持续电能,需要先对一些必要的参数进行合理化的选取,如初始投资费用、充电效率、充电服务半径等。部分参数设置如表2所示。 表2 规划区内参数选取 计划在规划区内建设充电站供电动汽车补给电量,通过粗略计算确定需要建设5座充电站,现有10座候选充电站的位置如表3所示。 表3 候选充电站坐标 在这里采用PSO和改进后的LWGPSO算法分别对选址问题进行编码,运用MATLAB对实例编写程序,可以得到模型的优化结果。最终确定充电站及服务小区分别如表4、表5所示。 表4 (PSO算法)充电站坐标及服务小区 表5 (LWGPSO算法)充电站坐标及服务小区 根据表4、表5所示的结果,我们可以确定出LWGPSO算法求得的充电站的选址分布情况,如图1所示。两种算法求解的迭代图如图2所示。 图1 LWGPSO算法确定的充电站及服务小区 图2 两种算法的迭代曲线 从图2可知,PSO求解选址问题需要进化140代左右,最终确定的最优解函数值为48.6,经过计算得到充电站运行年费用为1 586.91万元;而经过优化后的LWGPSO算法只需要进化40代就能取得最优解函数值为48.3,波动次数少,经过计算得到充电站运行年费用为1 558.32万元。两种选址算法的性能比较如表6所示。 表6 两种选址算法结果比较 通过结果比较可以看出,对PSO算法优化并结合GA算法后,明显加快了算法求解的收敛速度。不仅减少了算法计算时间和迭代次数,同时也对目标数值有所优化。各个充电站服务划分明确,基本上符合就近充电原则,实现了费用和便利的双优化目标。 本文对影响充电站规划选址的因素进行深入分析,建立了合理化的选址模型,利用改进后的LWGPSO算法求解规划问题。改进后的算法处理问题时不仅更加准确,而且克服了PSO算法容易陷入局部最优、收敛速度慢等缺点,在一定程度上使得计算结果更优于传统算法。通过对算例的仿真求解,取得了相应的结果,并且更进一步验证了算法的可行性和模型的准确性,为充电站布局规划工作提供了一定的理论经验。 [1] 张宝中.新能源光伏汽车充电站发展现状与分析[J].科技与创新,2016(16):106-107. [2] 朱柯羽.城市电动汽车充电站选址规划研究[J].科技展望,2016,26(8):263-264. [3] 杨现青,刘法胜,杨玲玲,等.电动汽车充电站选址优化研究[J].交通科技与经济,2016,18(3):14-18. [4] 应夏辉,李锦霞.电动汽车充电站的选址优化研究[J].交通科技与经济,2014,16(1):43-46. [5] 冯超,周步祥,林楠.电动汽车充电站规划的多种群混合遗传算法[J].电力系统及其自动化,2013,25(6):123-129. [6] Pan Z J,Zhang Y.A novel centralized charging station planning strategy considering urban power network structure strength[J].Electric Power Systems Research,2016,136:100-109. [7] 杨铎.计及电动汽车电池集中充电站接入的电网稳定性分析[D].北京:华北电力大学电气与电子工程学院,2014. [8] 张俊溪,张嘉桐,张玉梅.一种改进的粒子群优化算法[J].陕西师范大学学报,2016,44(2):15-20. [9] 陈香.解决面试工作安排中专家资源合理分配问题[J].湖南农机,2014,41(10):29-30. LAYOUTOFCHARGINGSTATIONSBASEDONIMPROVEDPARTICLESSWARMOPTIMIZATIONWITHGENETICCROSSOVER Zhang Zhiyu Zhang Huilin Xu Hui Ye Yufeng (SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China) In order to plan the layout of electric vehicle charging station reasonably, this paper adopts an optimization scheme based on improved particle swarm optimization with genetic crossover. On the basis of traditional particle swarm optimization, the local extremum is introduced to optimize the speed updating formula, and the adaptive inertia weight is adopted. A new solution is generated by the cross operation of the optimal solution of the current population and each particle optimal solution. At last, the improved algorithm is used to solve the urban examples. The results verify the validity and accuracy of the model, and show that the improved algorithm can improve the convergence rate of 70% while getting the global optimal solution and effectively reduce the total cost, improve the convenience. Charging station Particle swarm optimization Genetic crossover Inertia weight TP3 TP18 A 10.3969/j.issn.1000-386x.2017.10.049 2016-12-01。沪江基金资助项目(B1402/D1402)。张志宇,硕士生,主研领域:模式识别与人工智能。张会林,副教授。徐辉,硕士生。叶玉凤,硕士生。4 验证分析





5 结 语

