“学”中求“问”“问”中引“思”

陈荣芳

【摘要】问题是思维的重要特征，培养学生的问题意识需要在教学中引导学生提出问题，学会梳理问题，理解问题的本质，培养提问的习惯，从而不断启发学生思维，激发学生探究欲望，促进学生深度学习。

【关键词】数学教学问题意识数学思维

问，是儿童的天性，是开启智慧的金钥匙，也是发展思维的助推器。然而实际情况是，儿童之“问”与学生的学习渐行渐远，学生在课堂上不提问，不会问，不敢问，也无权提问，学习变成单纯地接受知识的过程。美国教育家尼尔·博斯特曼说过：一旦你学会了提问，掌握提出有意义、恰当的和实质性问题的方法，你就掌握了学习的技巧。因此，教师应该注重学生问题意识的培养，让学生在“问”中思考，“问”中学习。

一、引导学生提出问题，不惜其“时”

我们都知道，提出一个问题比解决一个问题更为重要。但是在实际教学中，往往看到更重视教师提问的预设，重视问题探究的过程，却忽视学生提出问题能力的培养。如教学《三角形内角和》时，教师引导学生观察学具盒里两把三角尺，得出直角三角形的内角和是180°后，就会直接代替学生提问：是不是所有三角形的内角和都是180度呢下面，我们来进行探究。

引导学生进行猜想和验证是重要的，但是引导从直角三角形的内角和联想一般三角形的内角和，能够提出这样的问题同等重要，甚至更为重要。因为，这是学生思维从具体到一般的突破，是培养学生问题意识、推理能力和联想能力的良好契机。在教学中，教师要舍得花时间，引导学生思考，引导学生学会提问。

在教学这个内容时，有一位教师是这样引导的：

刚才大家通过测量，知道了这两个三角形的内角和是180度，你能初步得出什么结论

生1：三角形三个内角相加是180度。

师做疑问状：你能这样确定我们也只仅仅看了这两个三角形呀。

生2（补充）：这两个三角形都是直角三角形，我可以得出结论：直角三角形三个内角的和是180度。

师表扬：你的思维真严谨！根据刚才的活动，我们可以很有根据地得出直角三角形的内角和是180度。

教师进一步引导：这时候，你可以进行怎样的联想，会提出怎样的问题呢

生：我想问，是不是所有三角形三个内角的和都是180度呢

师：谁来评价他这个问题问得好不好

生：他问得很好。我们只是看到了直角三角形的内角和是180度，而三角形还包括锐角三角形和直角三角形，还要再研究其余的两类三角形，如果也是180度，那我们就可以得出结论：所有三角形的内角和都是180度了。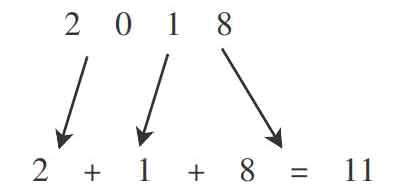

教室里响起了掌声。

教师在教学中放慢了节奏，不断鼓励，不断引导，不仅引导学生学会联想，提出问题，同时引导学生对提出的问题进行评价，能够自己提出问题并且寻求解决问题的方法。这样的教学，学生的问题意识增强，自主学习意识增强，探索和交流的意识也增强了。

二、引导学生梳理问题，不厌其“烦”

由于小学生的年龄特点，可能提出的问题是模糊的、不完整的，甚至还会是可笑的问题，教师要不厌其烦，认真对待学生提出的每一个问题，保护学生这种与生俱来的好奇心和敢于提问的自信心。通过讨论和梳理，让学生的“疑问”转化为“问题”，再引导学生逐渐提出有深度、有联系的问题。

在教学“认识人民币”时，教师布置学生观察这些钱币，引导学生提问：你有什么想问大家，或者问老师的吗

生：这些钱为什么有的大有的小

教师追问：你指的大小，是人民币样子有大有小，还是上面的币值有大有小

生1：我知道了，钱上面的数字大，这个钱的样子也就大，比如说：100元的要比10元的大。这时候，其他学生也拿带来的人民币进行比较，果真发现人民币每个币种的大小还真是不一样。

生2：为什么硬币只有1元和5角

师：有谁能解答他这个问题吗

生：我知道，因为硬币一般是打电话投币，或者是坐公交车投币用的，所以只要这两种就可以用了。

教师表扬：他能够联系我们平时的生活实际进行思考，非常好！

生1：为什么有关角的钱，只有1角、2角和5角

生2：我也发现有关元的钱，也只有1元、2元和5元。

生3：不对，还有10元、20元、50元和100元。

生4：为什么最大的人民币是100元

师：我们先来讨论讨论，为什么人民币有1角、2角和5角还有1元、2元和5元呢

在教师的引导下，学生通过讨论，终于弄明白了人民币为什么没有3、4、6、7、8、9这些面值，在1～10这10个自然数里，用1、2、5、10这些数可以得出其他的几个数，如1+2=3、2+2=4、1+5=6、2+5=7、10-2=8、10-1=9，这些数就是“重要数”，用这几个数就能以最少的加减组成另一些数，这样做也是为了简化和节省成本。

为什么人民币币值最大的是100元，教师进行了讲解：目前社會的钱币实际需求量，方便使用和兑换，所以这样设置。还有学生补充说：现在很多付钱的时候可以用银行卡，还有微信、支付宝，所以不需要太大的面额，看来学生已经学会将数学和生活进行联系了。

以上学习过程中，学生提出了许多自己的疑问，教师并没有感到厌烦，而是满足学生的好奇心，组织学生进行讨论，必要的时候进行讲解。一方面充分尊重学生，表扬了学生的“敢说敢表达”，学生真正成为学习的主人；另一方面，引导学生讨论，将“疑问”转化为“问题”，经历这些问题的提出和解决过程，对数学学科的本质有了深刻体会，对数学和生活的联系也有了深厚体会，树立了数学学习的积极情感。endprint

三、引导学生理解问题，寻求其“联”

在数学学习中，学生一开始提出的问题往往是浮于表面，松散和零乱的，教师要引导学生学会联系起来看问题，沟通过去已有知识经验，联想到未来可能会学习什么知识，学会透过现象看到本质，发现现象和本质背后的联系，在问题中学会思考。

在学习“小数加减法”的时候，学生很自然地会提出问题：为什么将小数点对齐而不是小数末尾对齐呢教师就要引导学生联系小数的意义、小数的数位和计数单位来进行理解，让学生理解在小数的计数中，小数点是一个标准，小数点对齐了，数位就对齐了。如果将有不同位数的小数末尾对齐，那相同的数位就不能对齐了。而整数加减法的时候是以个位为标准，个位对齐了，那其他数位也就对齐了。在解决学生的问题后，教师没有仅仅停留在小数加减法的算理的理解，而是立足于知识的整体建构，出示了这样一组题：

4（○）+5（○）=

400+500=

0.4+0.5=

420+520=（）（）

学生解答后，教师引导观察：我们不仅要做题目，还要学会将这些题目联系起来比较，你可以提出什么问题

学生提出问题：这四道题有什么相同的地方还有什么不一样的地方

学生找到题目中都进行了4+5的运算，教师让学生分别说一说每道题是4个（）加上5个（）等于9个（）。根据学生的回答板书：

4个（○）+5个（○）=9个（○）

4个（百）+5个（百）=9个（百）

4个（0.1）+5个（0.1）=9个（0.1）

4个（20）+5个（20）=9个（20）

通过引导，学生发现了4个相同的单位加上5个相同的单位，就得到9个这样的相同单位。虽然加法的类型不一样，但是不同类型算式背后的原理是一样的，就是相同单位的数相加，单位不变，单位的个数进行相加。通过这样的一根“线”，将原有的知识和现在所学的知识进行了结构的构建，学生学会了有联系地、结构化地看待问题。

四、引导学生学会追问，立足其“深”

在教学2、5、3的倍数的特征时，学生自然会产生这样的问题：判断一个数是不是2或5的倍数，为什么只要看个位判断一个数是不是3的倍数，为什么要看各数位上的数字之和很多教师认为，学生只要掌握判断的方法就可以了，不需要理解为什么这样判断。其实，这是一种狭隘的理解，如果学生不清楚规律背后的原因，就只能机械地记忆这些结论，当学生追问结论后面的“为什么”，才会理解知识的本质，达到思维的深刻性，进一步激发学生学习的欲望。

当学生提出这样的问题后，有一位教师是这样引导学生进行理解的：

师：我们先来解决这个问题，判断一个数是不是2或者5的倍数，为什么只要看个位

生1：我知道了！10、100、1000这些数都是2或者5的倍数，所以不需要一个一个地看，只要看个位就可以了。

生2进行解释：比如，我们在分东西的时候，2个2个地分，几十、几百、几千都可以正好分完，所以不用看十位、百位、千位上的数，只要看个位上能不能正好分完就可以了。

生3：5个5个地分，也是一样的。

师：那10、100、1000这些数，如果3个3个地分，会出现什么情况呢

师生一起来计算：

10÷3=3……1

100÷3=33……1

1000÷3=333……1

教师引导学生观察，得出结论：十位、百位、千位上的数不能正好分完，所以不能只看个位了，而是每个数位上的数都要看一看。

师：那怎么来判断呢我们可以举出一个例子来试一试。

教师和学生一起判断2018÷3，可以将2018个苹果看作2箱（每箱1000个），加上1盒（每盒10个）和8个苹果，3个3个地分，可以先分2箱，还余2个苹果，再分1盒，余1个，再加上最后的8个，应该就是2+1+8=11，不能正好分完。教师结合回答，进行板书：

2018

2+1+8=11

师：我们来看看，这里的2表示什么1呢8呢

生：千位上3个3个地分，剩2个；十位上3个3个地分，剩1个；个位上剩8个，可以将剩下来的合起来再一起分，就可以知道能不能被3整除了。

教师总结：原来，各数位上的数之和，就是把各数位上分剩下来的数合在一起相加，看看最终能不能被3整除。

在上述教学片段上，教师引导学生将3的倍数的特征与3的倍数的意义（3个3个地分，刚好分完）联系起来思考，把较难的知识变得容易理解，在理解的基础上学生能够明白判断3的倍数为什么要看各数位上的数字之和。同时在思想方法上也与2和5的倍数特征统一进行理解，完善了学生的认知结构。

这样的教学，引导学生学会追问，探究规律背后的原理，把知识的教学拓展向更为基础、更普遍的内容相联系向纵深处理解，，使学生有“恍然大悟”“原来如此”之感。这样的“深”是一种沟通，让学生把所学的知识与已有的知识、经验和方法建立了强有力的联系，构建了知识的网络系统。

五、培养学生问题意识，注重其“长”

培养学生的问题意识，不是一节课就能完成的，而是要立足学生的长远发展，在每个环节、每个章节的教学时，引导学生学会从一些生活或数学现象中找到数量关系或者空间关系之间的联系或者矛盾，并把这些联系和矛盾進行提炼，使用数学语言、数学符号，以“问题”的形态表述出来，时时、处处渗透学生问题意识的培养。

例如，在学习了用一副三角板能拼出几个钝角的问题后，就要引导学生学会联想和提问：如果用两副三角板呢再如，在学习了三角形的内角和之后，教师要引导学生思考：如何求出四边形、五边形的内角和呢还可以提问：三角形有内角的和，那么三角形外角的和是多少度呢四边形、五边形外角的和又是多少度呢

问题是思维的重要特征，教学中应该以问题为开端，引导学生发现问题、提出问题，在分析和解决的过程中拓展思维张力，体验探究的魅力，激发好奇心和求知欲，开展深度而又有意义的学习，使学生获得生长的力量。endprint